DOI: 10.11817/j.issn.1672-7207.2015.01.021
基于鲁棒局部嵌入的孪生支持向量机
花小朋1, 2, 3,丁世飞1, 2
(1. 中国矿业大学 计算机科学与技术学院,江苏 徐州,221116;
2. 中国科学院计算技术研究所 智能信息处理重点实验室,北京,100190;
3. 盐城工学院 信息工程学院,江苏 盐城,224051)
摘要:针对已有非平行超平面支持向量机(NHSVM)分类方法仅考虑训练样本的全局信息却忽视训练样本之间局部几何结构的问题,将鲁棒局部线性嵌入(ARLE)方法的基本思想引入NHSVM中,提出一种基于鲁棒局部嵌入的孪生支持向量机(ARLEBTSVM)。该方法不但继承NHSVM方法具有的异或(XOR)问题处理能力;而且可以很好地保持训练样本空间的局部信息,同时通过考虑样本的全局分布来自动抑制野值样本点对嵌入的影响,从而在一定程度上提高分类算法的泛化性能。为了更好地处理非线性分类问题,通过核映射方法构造非线性ARLEBTSVM。在人造数据集和真实数据集上进行实验,结果表明ARLEBTSVM方法具有更好的分类性能。
关键词:分类;非平行超平面支持向量机;局部线性嵌入;异或问题;核映射
中图分类号:TP391.4 文献标志码:A 文章编号:1672-7207(2015)01-0149-08
An alternative robust local embding based on twin support vector machines
HUA Xiaopeng1, 2, 3, DING Shifei1, 2
(1. School of Computer Science and Technology, China University of Mining and Technology, Xuzhou 221116, China;
2. Key Laboratory of Intelligent Information Processing, Institute of Computing Technology,
Chinese Academy of Sciences, Beijing 100190, China;
3. School of Information Engineering, Yancheng Institute of Technology, Yancheng 224051, China)
Abstract: Aiming at the problem that many existing nonparallel hyperplane support vector machine (NHSVM) methods only considered the global information of the training samples in the same class and did not fully take into account the local geometric structure and the underlying descriminant information, an alternative robust local embedding based twin support vector machine (ARLEBTSVM) was presented by introducing the basic theories of alternative robust local embedding (ARLE) algorithm into the NHSVM. ARLEBTSVM not only inherits the characteristic of NHSVM methods which can well deal with the XOR problem, but also fully considers the local and global geometric structure of training samples in the same class and shows the local and global underlying discriminant information. In addition, in order to well deal with the nonlinear classification problem, the kernel mapping method was used to extend ARLEBTSVM to the nonlinear case. Experimental results on some artificial datasets and many real UCI datasets indicate that the proposed ARLEBTSVM method has better classification ability.
Key words: classification; nonparallel hyperplane support vector machine; locally linear embedding; xor problem; kernel mapping
对于二分类问题,传统SVM依据大间隔原则生成单一的分类超平面[1]。存在的缺陷是计算复杂度高且没有充分考虑样本的分布[2]。近年来,作为SVM的拓展方向之一,非平行超平面支持向量机(nonparallel hyperplane SVM, NHSVM)分类方法正逐渐成为模式识别领域新的研究热点。该类方法的研究源于Mangasarian和Wild在TPAMI上提出的广义特征值近似支持向量机(generalized eigenvalue proximal SVM, GEPSVM)[3]。GEPSVM摒弃了近似支持向量机(proximal SVM, PSVM)中平行约束的条件,优化目标要求超平面离本类样本尽可能的近,离他类样本尽可能远,问题归结为求解2个广义特征值问题。与SVM相比,除了速度上的优势,GEPSVM能较好地处理异(XOR)问题[4-5]。基于GEPSVM,近年发展了许多NHSVM分类方法,如孪生支持向量机(twin SVM, TWSVM)[6]、投影孪生支持向量机(projection twin support vector machine, PTSVM)[7]、最小二乘孪生支持向量回归机[8]等。然而,经分析发现,已有的NHSVM分类方法在学习过程中仅考虑训练样本的全局分布,并没有充分考虑样本之间的局部几何结构及所蕴含的鉴别信息。为了有效揭示样本内部蕴含的局部几何结构,文献[9-12]分别提出了几种具有一定代表性的流行学习方法:等距映射(isometric mapping, IM)、局部线性嵌入(locally linear embedding, LLE)、拉普拉斯特征映射(laplacian eigenmap, LE)和局部保持投影(locality preserving projections, LPP)。这些方法假设数据位于高维空间中的低维流行上,通过与谱图理论相结合,分别从局部刻画了高维空间中的数据低维非线性流行,并在低维嵌入空间中保持了相应的流行结构。尽管这些算法能够更加有效地挖掘出数据的结构信息,但是其中的大部分算法对数据集中的野值都很敏感。而且基于局部的算法往往忽略了数据的全局结构信息,导致低维嵌入在反映数据流行结构时发生偏差[13]。文献[13]针对典型的局部非线性流行学习方法LLE,提出了一种新的无监督局部嵌入算法:鲁棒局部嵌入(alternative robust local embedding,ARLE)。ARLE充分考虑了数据流行的局部结构信息,而且自动地抑制了野值对嵌入的影响,具有比LLE更准确的嵌入。文献[14]将ARLE与SVM相结合,提出一种全局追求支持向量机(glocalization pursuit SVM, GPSVM)。然而,GPSVM属于单面支持向量机范畴。因此,本文作者将ARLE思想引入到NHSVM分类方法中,提出一种基于鲁棒局部嵌入的孪生支持向量机(alternative robust local embedding based twin SVM, ARLEBTSVM)。该方法具有如下优势:继承了NHSVM分类方法的特色,如线性模式下对XOR类数据集的分类能力;将ARLE思想引入NHSVM分类方法中,充分考虑了蕴含在样本空间中的局部及全局鉴别信息,从而在一定程度上可以提高算法的泛化性能; 采用核映射方法,ARLEBTSVM可以很容易进行非线性嵌入,得到非线性分类方法。
1 TWSVM和PTSVM的简单回顾
在已有的NHSVM分类方法中,TWSVM和PTSVM在泛化性能上要优于其他分类方法[6-7]。因此,本文选择这2种非平行超平面支持向量机分类方法作为比较分析对象。
1.1 TWSVM
给定两类n维的m个训练样本点,分别用m1×n的矩阵A和m2×n的矩阵B表示+1类和-1类,这里m1和m2分别是两类样本的数目,并令m=m1+ m2。TWSVM的目标是在n维空间中寻找2个超平面:
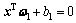 ,
,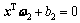 (1)
(1)
要求每个类超平面离本类样本尽可能近,离他类样本尽可能远。第1类超平面的优化准则为
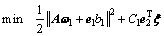
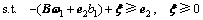 (2)
(2)
其中: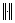 表示L2范数;C1为惩罚参数;x为损失变量;e1和e2是2个实体为1的列向量;A=
表示L2范数;C1为惩罚参数;x为损失变量;e1和e2是2个实体为1的列向量;A=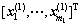 ;B=
;B=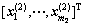 ;
;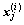 表示第i类的第j个样本。
表示第i类的第j个样本。
显然,TWSVM优化目标函数中没有考虑到训练样本内部局部几何结构中蕴含的鉴别信息。
1.2 PTSVM
PTSVM的目标也是在n维空间中寻找两个投影轴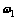 和
和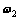 ,要求本类样本投影后尽可能聚集,同时他类样本尽可能分散。PTSVM对应的2个决策超平面为
,要求本类样本投影后尽可能聚集,同时他类样本尽可能分散。PTSVM对应的2个决策超平面为
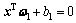 ,
,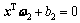 (3)
(3)
需要注意的是,这里的偏置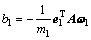 ,
,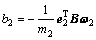 。
。
第1类超平面的优化准则为
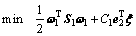
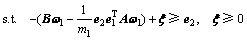 (4)
(4)
其中:S1是第1类样本的类内方差。
显然,PTSVM的优化目标函数考虑的是样本的散度,类内方差S1反应的是样本的全局分布,不是样本之间的局部几何结构。因此,该方法也没有考虑蕴含在样本之间局部鉴别信息。
2 基于鲁棒局部嵌入的孪生支持向量机(ARLEBTSVM)
文献[13-14]从理论和实验上系统分析了ARLE方法可以有效的保持样本空间局部几何结构信息,而且可以自动抑制野值对嵌入的影响,所以,本文的ARLEBTSVM方法通过引入ARLE的思想以达到保持样本内在的局部及全局几何结构是合理的。
2.1 线性ARLEBTSVM
定义1[14] 假定X1=A,X2=B,则第c(c=1, 2)类样本的类内局部及全局保持散度矩阵为
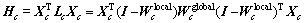
其中:
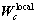 (
(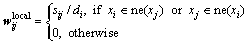 ,为局部权矩阵;
,为局部权矩阵;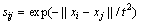 (t为热核参数);
(t为热核参数);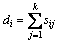 ;
;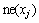 为
为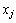 的k近邻;
的k近邻;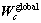 = diag[
= diag[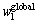 , …,
, …, 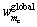 ]为全局权矩阵;(
]为全局权矩阵;(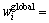
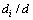 ,
,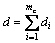 ;I为单位矩阵。
;I为单位矩阵。
局部及全局保持类内散度矩阵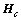 是对称的正半定矩阵,其思想源于ARLE,它反映了第c类样本空间的内在局部及全局几何结构[13-14]。
是对称的正半定矩阵,其思想源于ARLE,它反映了第c类样本空间的内在局部及全局几何结构[13-14]。
定义2 线性ARLEBTSVM对应的第1类超平面优化准则为
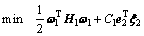
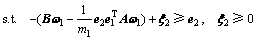 (5)
(5)
第2类超平面优化准则为
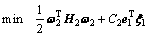
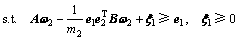 (6)
(6)
定理1 线性ARLEBTSVM优化准则式(5)对应的对偶问题为
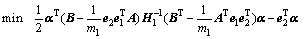
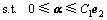 (7)
(7)
优化准则式(6)对应的对偶问题为
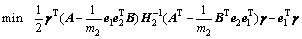
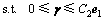 (8)
(8)
证明 考虑线性ARLEBTSVM的优化准则式(5),对应的拉格朗日函数为
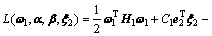
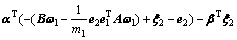 (9)
(9)
其中: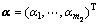 ;
;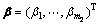 为非负拉格朗日系数。
为非负拉格朗日系数。
根据Karush-Kuhn-Tucker(KKT)[15]条件可得:
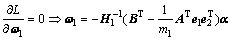 (10)
(10)
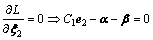 (11)
(11)
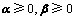 (12)
(12)
将式(10)~(12)代入式(9)得定理1中式(7)成立。
同理可证得定理1中式(8)成立,且
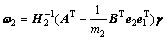 (13)
(13)
证毕。
通过求解定理1中2个对偶问题,可以分别求得拉格朗日系数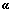 和
和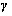 ,并在此基础上求出两类样本的投影轴
,并在此基础上求出两类样本的投影轴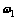 和
和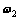 。类似于PTSVM,线性ARLEBTSVM的2个决策超平面为
。类似于PTSVM,线性ARLEBTSVM的2个决策超平面为
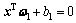 ,
,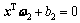 (14)
(14)
其中:偏置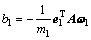 ;
;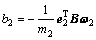 。
。
线性ARLETSVM的决策函数为
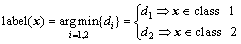 (15)
(15)
其中: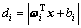 ;
; 表示绝对值。
表示绝对值。
从式(10)和(13)可知:ARLEBTSVM在求解过程中需要计算局部及全局保持类内散度矩阵Hc(c=1,2)的逆矩阵,而Hc是正半定矩阵,因此,该方法不是严格的凸规划问题(强凸问题),特别是在小样本情况下确实存在矩阵Hc的奇异性。文献[6]通过引入规则项eI(e>0)解决TWSVM存在的奇异性问题,文献[7]采用类似于PCA降维的方法解决PTSVM存在的奇异性问题。这里采用文献[6]的方法,即ARLEBTSVM方法中Hc 用(Hc+eI)替代,e尽可能地小。这样既可以解决Hc的奇异性,又能保证(Hc+eI)近似于Hc[5]。
2.2 TWSVM,PTSVM和ARLEBTSVM比较
2.2.1 泛化能力
考虑ARLEBTSVM优化目标函数第一项中局部及全局保持类内散度矩阵Hc。局部权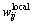 反映了样本点xj相对于xi的邻近程度,其值越大,意味着越有可能是附近的正常样本点,反之,xj可能是离群点。同样,全局权
反映了样本点xj相对于xi的邻近程度,其值越大,意味着越有可能是附近的正常样本点,反之,xj可能是离群点。同样,全局权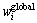 反映了样本点xi的局部邻域相对于整个流行结构的自信度,其值越大,表示xi的局部邻域越能刻画样本空间的局部几何结构。以上分析说明ARLEBTSVM充分有效考虑了蕴含在样本间局部及全局几何结构中的鉴别信息。而TWSVM和PTSVM正如1.1及1.2节分析,两者均没有考虑样本空间的局部信息。
反映了样本点xi的局部邻域相对于整个流行结构的自信度,其值越大,表示xi的局部邻域越能刻画样本空间的局部几何结构。以上分析说明ARLEBTSVM充分有效考虑了蕴含在样本间局部及全局几何结构中的鉴别信息。而TWSVM和PTSVM正如1.1及1.2节分析,两者均没有考虑样本空间的局部信息。
图1所示为TWSVM,PTSVM和ARLEBTSVM在人造数据集上的决策超平面。显然,ARLEBTSVM明显区别于TWSVM和PTSVM。ARLEBTSVM的2个超平面反映了2类样本的内在局部流行结构; 而TWSVM与PTSVM类似,它们反映的都是每类样本分布的平均信息。图1也进一步证明了TWSVM和PTSVM确实没有考虑蕴含在样本间局部几何结构中的鉴别信息。
2.2.2 时间复杂度
TWSVM,PTSVM和ARLEBTSVM 3种算法的计算时间消耗主要集中在2次规划求解上,而三者2次规划求解规模相当,所以,宏观上,三者的计算时间复杂度均为O(m13+m23)。
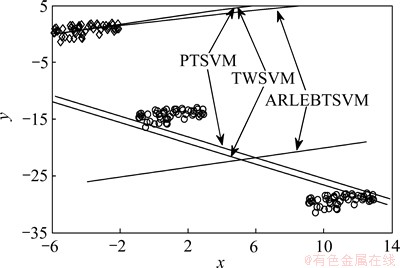
图1 ARLEBTSVM,TWSVM与PTSVM三者在人造数据集上的决策超平面
Fig. 1 Illustration of decision hyperplanes generated by TWSVM, PTSVM and ARLEBTSVM
2.3 非线性ARLEBTSVM
当样本内在的几何结构呈现出高维非线性流行时,线性ARLEBTSVM方法是没有办法得到非线性流行结构的,因此,本文提出非线性ARLEBTSVM方法。定义一非线性函数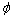 将样本x映射到特征空间
将样本x映射到特征空间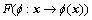 ,再引入核函数
,再引入核函数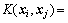
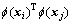 ,结合特征空间再生理论[14]可以将特征空间中的非线性决策超平面法向量表示为:
,结合特征空间再生理论[14]可以将特征空间中的非线性决策超平面法向量表示为: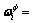
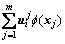 (其中,
(其中,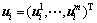 表示权值矢量;i=1, 2)。这样,式(5)和(6)目标函数中的正则化单 元
表示权值矢量;i=1, 2)。这样,式(5)和(6)目标函数中的正则化单 元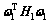 和
和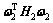 可分别转换成特征空间中 的正则化单元
可分别转换成特征空间中 的正则化单元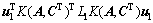 和
和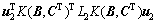 ,其中
,其中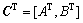 。
。
定义3 非线性ARLEBTSVM对应的第1类超平面优化准则为
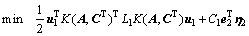
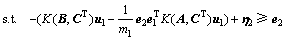 ,
,
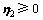 (16)
(16)
第2类超平面优化准则为
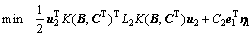
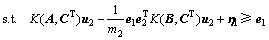 ,
,
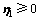 (17)
(17)
定理2 非线性ARLEBTSVM优化准则式(16)对应的对偶问题为
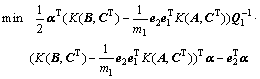
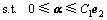 (18)
(18)
优化准则式(17)对应的对偶问题为
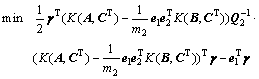
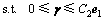 (19)
(19)
其中: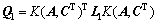 ;
;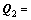
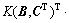
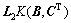 。
。
证明 考虑非线性ARLEBTSVM的优化准则式(16)。式(16)对应的拉格朗日函数为
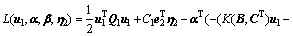
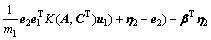 (20)
(20)
根据Karush-Kuhn-Tucker(KKT)[15]条件可得:
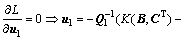
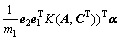 (21)
(21)
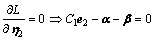 (22)
(22)
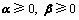 (23)
(23)
将式(21)~(23)代入式(20)得定理2中式(18)成立。
同理可证得定理2中式(19)成立,且
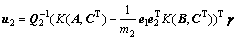 (24)
(24)
证毕。
非线性ARLEBTSVM的2个决策超平面为
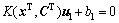 ,
,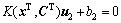 (25)
(25)
其中:偏置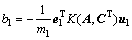 ;
;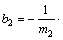
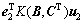 。
。
线性ARLEBTSVM的决策函数为
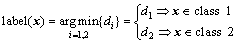 (26)
(26)
其中: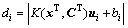 。
。
3 实验与分析
在人工数据集和真实数据集上分别对TWSVM,PTSVM与ARLEBTSVM进行实验。实验环境:Windows 7 操作系统,CPU为i3-2350M 2.3GHz,内存为2GB,运行软件为MATLAB 7.1。
3.1 测试人造数据集
人造数据集经常被用来测试算法效果[2],这里分别使用交叉数据集和流行数据集来验证本文ARLEBTSVM分类性能,并与TWSVM和PTSVM进行对比。
3.1.1 测试交叉数据集
相对于单面支持向量机,线性模式下对XOR问题的求解能力是NHSVM分类算法优势之一[3-4, 6]。因此,这里首先验证ARLEBTSVM求解XOR的能力。图2给出了TWSVM,PTSVM与ARLEBTSVM 3个分类器在交叉数据集上“Crossplanes”(XOR的推 广)[3-4, 6]上的分类性能。显然3个算法产生的分类面重合,而且可以较好的求解XOR问题,并得到100%的学习精度。这也进一步证明了本文ARLEBTSVM继承了NHSVM分类算法的特色,即线性模式下对XOR问题的求解能力比单面支持向量机算法的求解能力强。
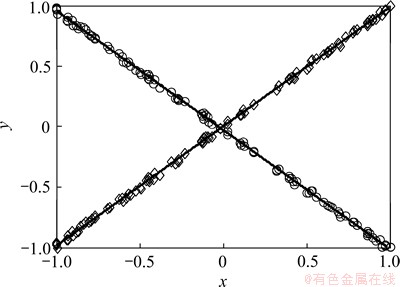
图2 TWSVM,PTSVM和ARLEBTSVM在交叉数据集上产生的分类面
Fig. 2 Planes generated by TWSVM, PTSVM and ARLEBTSVM on “cross planes” dataset
3.1.2 测试流行数据集
数据集two-moons经常被用于测试一些流行学习方法[2]。这里通过与TWSVM和PTSVM方法进行比较,测试本文方法在2种不同复杂度two-moons数据集(图3(a)和图3(b))上保持非线性局部流行结构的性能。
实验设计:2种two-moons数据集均为100,其中正负类数据数各50,随机抽取40%训练集和60%测试集,重复10次,分别记录实验结果,且计算实验结果的平均值如表1所示。参数C1与C2的搜索范围均为{2i|i=-7, -4, -1, 0, +3, +7, +10};核函数选用GAUSS核,核参数搜索范围为{10i|i=-3, -2, -1, …, +3};规则项中e取值10-6。ARLEBTSVM中热参数t的搜索范围为{2i|i=1, 2, …, 7},近邻数k的搜索范围为{1, 2, …, 10}。
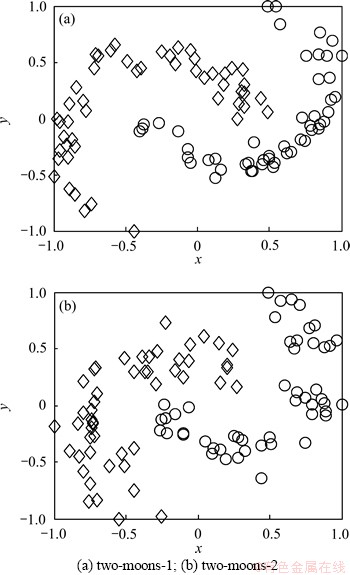
图3 2种不同复杂度的two-moons数据集
Fig. 3 Two kinds of two-moons datasets with different complexity.
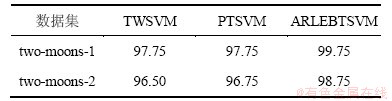
从表1可以看出:1) ARLEBTSVM方法对于流行数据集的测试性能比TWSVM和PTSVM方法的高,这也进一步证明了本文方法能够更好地保持样本间非线性局部流行结构鉴别信息。2) 对于two-moons-1,ARLEBTSVM测试精度比TSVM和PTSVM平均高2.00%。对于two-moons-2,ARLEBTSVM测试精度比TWSVM和PTSVM平均高出2.25%。这表明,当数据集的拓扑结构变得更加复杂而不规则时,本文ARLEBTSVM仍然保持较好的泛化性能。
表1 TWSVM,PTSVM 和 ARLEBTSVM算法的测试精度比较
Table 1 Classification accuracy of TWSVM, PTSVM and ARLEBTSVM on two kinds of two-moons Datasets %
3.2 测试真实数据集
为了更全面地说明本文ARLEBTSVM分类方法具有的分类性能,测试UCI数据集,同时与TWSVM,PTSVM进行对比。
UCI数据集经常被用来测试算法的分类精度[4-7, 16-17]。在该测试阶段,抽取该数据集的8个分类数据子集:Hepatitis,Sonar,Glass_12,P_gene,Wpbc,Cleve,Spectf和Haberman来分别测试TWSVM,PTSVM和本文GLPBTSVM。对于每个数据子集,选用5-折交叉验证方法[16]。3种方法均采用SOR[18]技术进行2次规划求解,实验结果为平均识别精度和训练时间。相关参数搜索范围与3.1.2节中的相同。表2和表3所示分别为线性模式及非线性模式下3种分类方法的测试结果。
表2 线性TWSVM,PTSVM与ARLEBTSVM的测试结果
Table 2 Linear Kernel Comparison for TWSVM, PTSVM and ARLEBTSVM
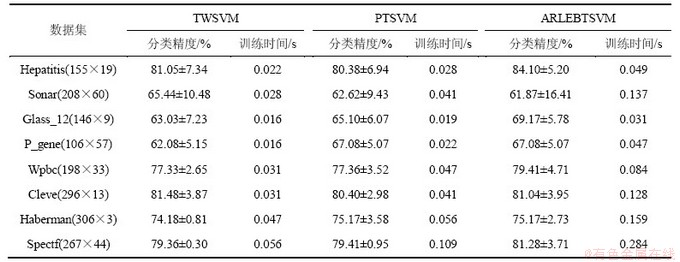
表3 非线性TWSVM, PTSVM与ARLEBTSVM的测试结果
Table 3 Nonlinear Kernel Comparison for TWSVM, PTSVM and ARLEBTSVM
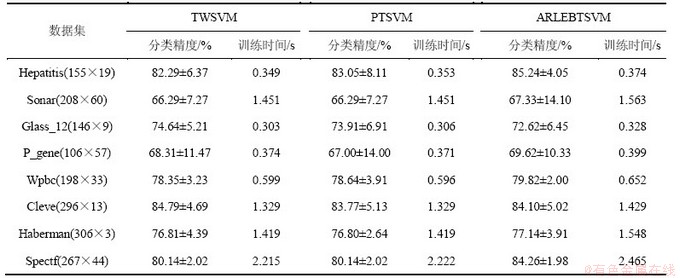
从泛化性能上看,无论是线性模式还是非线性模式,本文的ARLEBTSVM方法对未知样本的识别精度总体上均比TWSVM和PTSVM的高。这进一步表明,充分考虑样本空间局部及全局结构信息确实能够在一定程度上提高多面分类器的泛化性能。
从训练时间上看,宏观上,3种方法基本处于同样的数量级,这主要是因为3种算法的时间复杂度主要都集中在2次规划求解上,而三者2次规划求解的规模相当;微观上,本文的ARLEBTSVM要略慢于TWSVM和PTSVM,从实验过程上看,这主要是因为ARLEBTSVM中Hc计算包含计算最近邻图信息,所以计算量偏高。
4 结论
1) 根据已有NHSVM方法存在的不足,将ARLE基本原理引入NHSVM中,提出一种新的方法即ARLEBTSVM。该方法不仅继承了NHSVM方法较好的异或(XOR)问题的求解能力,而且在一定程度上克服了已有NHSVM方法没有充分考虑训练样本间局部几何结构信息的缺陷。
2) 对于非线性分类问题,本文采用核映射方法构造非线性特征空间,将线性方法拓展到非线性情况,提出非线性ARLEBTSVM方法。实验中选用具有代表性的TWSVM和PTSVM进行比较,结果表明本文ARLEBTSVM方法具有较好的泛化性能。
参考文献:
[1] 王雪松, 高阳, 程玉虎. 基于随机子空间—正交局部保持投影的支持向量机[J]. 电子学报, 2011, 39(8): 1746-1750.
WANG Xuesong, GAO Yang, CHENG Yuhu. Support vector machine based on random subspace and orthogonal locality preserving projection[J]. Acta Electronica Sinica, 2011, 39(8): 1746-1750.
[2] 皋军, 王士同, 邓赵红. 基于全局和局部保持的半监督支持向量机[J]. 电子学报, 2010, 38(7): 1626-1633.
GAO Jun, WANG Shitong, DENG Zhaohong. Global and local preserving based semi-supervised support vector machine[J]. Acta Electronica Sinica, 2010, 38(7): 1626-1633.
[3] Mangasarian O L, Wild E. MultisurFace proximal support vector machine classification via generalized eigenvalues[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(1): 69-74.
[4] 业巧林, 赵春霞, 陈小波. 基于正则化技术的对支持向量机特征选择算法[J]. 计算机研究与发展, 2011, 48(6): 1029-1037.
YE Qiaolin, ZHAO Chunxia, CHEN Xiaobo. A feature selection method for TWSVM via a regularization technique[J]. Journal of Computer Research and Development, 2011, 48(6): 1029-1037.
[5] Ding S F, Yu J Z, Qi B J. An overview on twin support vectormachines[J]. Artificial Intelligence Review, 2014, 42(2): 245-252.
[6] Jayadeva, Khemchandai R, Chandra S. Twin support vector machines for pattern classification[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2007, 29(5): 905-910.
[7] Chen X B, Yang J, Ye Q L, et al. Recursive projection twin support vector machine via within-class variance minimization[J]. Pattern Recognition, 2011, 44(10): 2643-2655.
[8] Huang H J, Ding S F, Shi Z Z. Primal least squares twin support vector regression[J]. Journal of Zhejiang University: Science C, 2013, 14(9): 722-732.
[9] Tenenbaum J B, Silva V D, Langford J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290(5500): 2319-2323.
[10] Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500): 2323-2326.
[11] Belkin M, Niyogi P. Laplacian eigenmaps for dimensionality reduction and data representation[J]. Neural Computation, 2003, 15(6): 1373-1369.
[12] He X F, Niyogi P. Locality preserving projection[EB/OL]. [2012-07-08]. http://www.docin.com/p-202458452.html.
[13] Xue H, Chen S. Alternative robust local embedding[C]// The International Conference on Wavelet Analysis and Pattern Recognition (ICWAPR). Beijing, 2007: 591-596.
[14] Xue H, Chen S. Glocalization pursuit support vector machine[J]. Neural Computing and Applications, 2011, 20(7): 1043-1053.
[15] 邓乃杨, 田英杰. 支持向量机: 理论、算法与拓展[M]. 北京: 科学出版社, 2009: 11-17.
DENG Naiyang, TIAN Yingjie. Support vector machine: Theory, algorithm and extension[M]. Beijing: Science Press, 2009: 11-17.
[16] Wang X M, Chung F L, Wang S T. On minimum class locality preserving variance support vector machine[J]. Patter Recognition, 2010, 43(8): 2753-2762.
[17] Ding S F, Hua X P. Recursive least squares projection twin support vector machines for nonlinear classification[J]. Neurocomputing, 2014, 130(4): 3-9.
[18] Shao Y H, Zhang C H, Wang X B, et al. Improvements on twin support vectot machines[J]. IEEE Transactions on Neural Networks, 2011, 22(6): 962-968.
(编辑 杨幼平)
收稿日期:2014-02-26;修回日期:2014-04-30
基金项目(Foundation item):国家重点基础研究发展规划(973计划)项目(2013CB329502);国家自然科学基金资助项目(61379101) (Project (2013CB329502) supported by Major State Basic Research Development Program of China; Project (61379101) supported by the National Natural Science Foundation of China)
通信作者:丁世飞,教授,博士生导师,从事机器学习与数据挖掘研究;E-mail: dingsf@cumt.edu.cn