软土路基粘弹塑性大应变分析的工程应用

何  群，魏丽敏，王永和

 (中南大学 土木建筑学院，湖南 长沙，410075)

摘  要：采用粘弹塑(西原)本构关系模拟土骨架的材料非线性、更新的拉格朗日法描述软土的几何非线性，推导用于增量分析的饱和土体双重非线性U.L.J.格式平衡方程和连续性方程，编制软土路基大型实用化有限元分析程序，利用该程序对某高速公路的实测断面分别进行大应变、小应变分析。数值模拟结果和现场实测结果的对比分析表明：大、小应变分析结果的差异随应力水平的提高和时间的延长而上升，其地表沉降、地基沉降、水平位移、孔隙水压力的最大相对误差分别为16.39%，20.23%，27.8%和22.75%，说明对软土路基进行大应变分析很有必要；采用室内试验确定的计算参数进行分析时，计算结果虽能较好地模拟地基应力和位移的发展趋势，但其值有较大差别，说明必须寻求更加合理的计算参数确定方法以提高数值模拟精度。

关键词：大应变；粘弹塑性本构关系；软土路基；沉降量；水平位移；孔隙水压力

中图分类号：U213.14         文献标识码：A         文章编号：1672-7207(2009)02-0512-07

Application of large strain analysis of visco-elastic-plastic soft soil subgrade

HE Qun, WEI Li-min, WANG Yong-he

(School of Civil and Architectural Engineering, Central South University, Changsha 410075, China⊙)

Abstract: The visco-elastic-plastic constitutive relation was employed to simulate the material non-linear of soil skeleton and the update lagrangian formulation was chosen to describe the geometry non-linear of soft soil. The continuity equation and double non-linear equilibrium equation of U.L.J. form for increment analysis of saturated soil were derived. The large-scale practical finite element analysis program was developed. The comparison analysis between large strain and small strain for a practical monitoring project on expressway was performed using this program. The analysis results were compared with the monitoring data. The results show that the difference of calculation results between large strain and small strain increases with the increase of stress level and time, the maximums of fractional error are 16.39% for settlement on the ground surface and 20.23% under the surface 3.8 m, 27.8% for horizontal deformation and 22.75% for pore water pressure, which show that the large strain analysis is indispensable for soft soil subgrade. When the calculating parameters determined by the laboratory test are adopted, though the developing trends of deformation and stress of subgrade are described well by FEM analysis, the differences between the calculating value and tested data are too large to be accepted, which shows that seeking for more rational methods to determine the calculating parameters is essential to improve the precision of numerical analysis.

Key words: large strain; visco-elastic-plastic constitutive relationship; soft soil subgrade; settlement; horizontal deformation; pore water pressure

由于软土的含水量高，孔隙比大，在自重或地面荷载作用下其变形量较大^[1]，有的甚至占初始土层厚度的一半以上^[2]，往往超出了小应变范畴。一些研究者除采用地基加固、轻质填料^[3]等工程措施减小地基沉降量外，还对大变形固结问题进行了研究，例如：Cargill^[4]采用Gibson的一维大变形固结方程研究土体的大变形特性，但由于难以扩展到二维和三维情况，其应用受到限制；Carte等^[5]基于欧拉描述，建立了一般形式的饱和土体三维大变形固结理论；Chopra等^[6]基于物质坐标，应用虚功原理推出了U.L.(Update Lagrangian)描述的大变形固结有限元方程；朱昊等^[7]使用拖带坐标描述饱和土的大变形固结特性；周正  明^[8]用加权残数法离散了一组大变形固结方程，并分析了大变形的影响；谢永利^[9]建立了物质描述的大变形固结问题的控制方程，推导了T.L.(Total Lagrangian)描述的大变形固结增量有限元公式，并引入自修正迭代算法对采用线弹性、非线性弹性Duncan-Chang和弹塑性剑桥模型的固结问题进行分析。但迄今为止，岩土工程中的几何非线性问题尚处于欠发展阶段，主要表现在：建立的非线性有限元基本方程存在不同形式，并未统一^[10]；有的研究者运用大变形固结分析所得任意时刻的沉降量大于小变形的沉降量^[8-9]，而有的研究者得出沉降量小于小变形的沉降量^[11-12]。

可见，必须对软土路基进行大应变分析，从理论分析与数值模拟2个方面探索几何非线性对软土路基变形和应力特性的影响，提高软土路基分析准确度。

1  大应变渗透固结问题控制方程

对于饱和土体的渗透固结问题，分析研究所采用的基本方程除了一般固体力学问题的平衡方程、本构方程、几何方程外，还必须引入考虑流体、固体分担荷载的有效应力原理，孔隙流体平衡方程(Darcy定律)，以及考虑土骨架和流体协调变形的连续性方程。

1.1  有效应力原理

对于t时刻构形，用Kirchhoff应力张量描述的Terzghi有效应力原理的增量形式为

1.2  U.L.J.格式渗透固结问题平衡方程

1.2.1  U.L.J.格式虚功方程

将U.L.格式的方程应用于非弹性大应变分析时，由于用来联系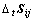和的本构关系式的材料常数不易确定，采用U.L.Jaumann应力率公式(简称U.L.J.公式)是行之有效的方法^[13]。U.L.J.使用的基本方程一是U.L.公式的增量虚功方程，用于计算增量位移；二是采用Jaumanny应力率方程描述本构关系，用于计算Cauchy应力。为保证最后导出的刚度矩阵的对称性，在非弹性大变形分析中，可忽略体积变形增量的影响。虚功方程中需要利用有效应力原理代换的应力增量，经整理得到U.L.J.格式的虚功方程：

1.2.2  U.L.J.格式虚功方程的线性化

略去方程(3)左端第2个体积积分的高阶非线性项，并参照文献[13]中的处理方式，将式(3)中的项忽略，得到线性化处理后的U.L.J.格式虚功方程：

1.3  渗流连续性方程

根据土颗粒和孔隙水不可压缩的基本假定，对饱和土体，从t构形到t+Δt 构形，单元体的体积变化率应等于流过物质单元3个方向表面上的流量变化之和，得

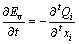。             (5)

式中：Q_i为单位时间内通过物质单元3个方向面上的单位流量；?E_v为以Green应变表示的体积应变的增量形式。将Darcy定律代入，可得渗透连续性方程：

若采用增量形式，并且不计渗透系数随坐标和时间的变化，则有

。          (7)

式中：^tk_i为t时刻构形上i方向的土体渗透系数，m/s；^tp_w为t时刻构形上的孔隙水压力，kPa；γ_w为水的重度，kN/m³。

2  粘弹塑本构关系的引入

2.1  模型选择

根据现场原状土样的室内长期蠕变试验结     果^[14-15]，该工点主要压缩层的变形特性可采用西原正夫模型描述，该模型由Hooke体、Kelvin体和Bingham体串联而成。尽管多维状态下流变模型很难用形象化的物理元件来表达，但流变方程可以参考一维模型，采用类比的方法直接得出^[16]，其应变仍可分解为弹性、粘弹性、粘塑性3部分，表示为

。        (8)

式中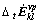：为粘塑性应变率增量张量。

2.2  Kelvin体本构方程

根据三维Kelvin粘弹性体的本构方程^[17]，可得其在恒定应力下的蠕变方程和对应的蠕变速率。由于路基施工过程中应力不断变化，需采用增量法。假定在Δt时段内应力为常量，则t+Δt 构形的应变及应变率的表达式分别为

2.3  Bingham体本构方程

假定粘塑性应变率只由当前应力确定，当采用相关联塑性流动法则时，

3  双重非线性渗透固结问题控制方程

3.1  双重非线性渗透固结问题平衡方程

由于渗透固结问题的弱形式的平衡方程——虚功方程式(4)是对拟弹性本构关系建立的，对于本文采用的粘弹塑性本构关系，需要进行进一步推导。

当使用相关联流动法则，采用显式法求解时，由式(8)可得粘弹塑性问题的增量型本构关系：

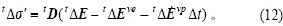
用式(12)代替式(4)中的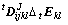，并将其中的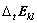分解为线性应变增量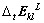和非线性应变增量，然后，将含有粘弹性应变增量和粘塑性应变率增量的项移至方程右端，可得到粘弹塑大应变渗透固结问题平衡方程：

3.2  双重非线性渗透固结问题有限元方法

根据有限元基本思想，选用增量有限元法求解。参考谢永利等^{[9, 19]}的计算成果，本文对位移和孔隙水压力同取一次插值模式，对上述平衡方程进行等参元离散，对连续性方程进行空间和时间离散^[9]，建立了考虑渗透固结问题的双重非线性有限元列式和迭代求解算法，并编制了大型实用化有限元分析程序LSVEP^[15]，该程序可利用“生”、“死”单元模拟路基施工的填筑和超载卸除过程。

4  试验工程与计算参数

4.1  试验工程概况

试验工程位于广东省西部沿海高速公路上，以K77+680断面为例，断面尺寸见图1。采用袋装砂井并预压加固法，砂垫层厚度为1.0 m，伸出坡脚外   1.0 m，内设2层土工格栅和1层土工布。袋装砂井直径为10 cm，按正三角形布置，间距为1.0 m，设计长度为13.3 m。路基填土高度为4.1 m，超载预压高度为2.0 m，超载预压期为300 d。在填筑及预压期间进行同步施工监测，监测项目包括地表沉降、深层沉降、坡脚水平位移、孔隙水压力等，测点布置见图1，监测结果见图2~7。

4.2  土层情况与计算参数

土层分布情况为：① 表层耕植土，厚度1.5 m；② 软塑~流塑状淤泥土，厚度约8.0 m；③ 软塑~可塑状含砾砂亚黏土。各土层计算参数由常规土工试验、长期蠕变试验和三轴试验确定^[15]，见表1。

5  数值模拟基本条件

5.1  计算区域的确定

考虑到路基的对称性，为减小计算工作量，取右侧路基为研究对象。根据现场实测结果，取地基计算域为L_C=70 m，H_C =30 m。边界条件为：对路基中线，水平位移为0，不透水；对地基下边界，竖向位移为0，不透水；对右边界，水平位移为0，透水；地基上表面、路堤上和右边界均为透水边界。

5.2 单元划分原则

为保证计算精度，同时便于与实测结果进行对比分析，在单元网格划分时遵循以下原则：

a. 四边形单元的长宽比l/b控制在l/b＜4；

b. 土层分界线(地下深度z为1.5 m和9.5 m)及地基处理界面(z =13.3 m)设置单元分界线；

c. 沉降板、分层沉降环及测斜管读数位置尽量设置为单元结点。

按上述原则划分的有限元网格，共设置地基单元21×10即210个，路堤单元12×9即108个。

单位：m

图1  K77+680监测断面元件布置图

Fig.1  Arrangement of test components for monitored section K77+680

表1  各土层计算参数

Table 1  Calculation parameters of every soil stratum

6  数值模拟与实测结果的对比分析

为了了解几何非线性对路基计算结果的影响程度及影响范围，利用研制的双重非线性渗透固结分析程序LSVEP模拟实际施工过程，对软土路基在路基填筑和预压期间的地基沉降、水平位移、孔隙水压力等，分别进行大变形、小变形有限元分析，并将计算结果与现场实测结果进行对比分析。

6.1  沉降量

路堤填筑过程参见图2(a)。路基中心线下，实测地表沉降量(测点CJB3-3)与有限元分析结果对比见图2(b)。图3所示为路基中心线下，深度3.8 m处计算沉降和深度3.859 m处实测沉降的对比结果。由图2和图3可见：

a. 由大应变、小应变有限元分析所得地基沉降量随施工进程的变化规律与实测沉降发展规律一致，且大应变分析所得沉降量比小变形分析所得沉降量大，其差异在施工前期很小，但随施工的进行日趋明显。这是因为随着路堤填筑高度的增加，应力水平不断提高。

(a) 路堤填筑过程；(b) 地表沉降量实测值与计算值对比

1—实测值；2—大应变计算值；3—小应变计算值

图2  地表沉降量实测值与计算值对比曲线

Fig.2  Comparison of calculated settlements with monitored settlements at ground surface

1—实测值, z=-3.8 m; 2—大应变计算值, z=-3.8 m; 3—小应变计算值, z=-3.859 m

图3  深度3.8 m处沉降计算值与实测值对比

Fig.3  Comparison of calculated settlements with monitored settlements at 3.8 m below ground surface

b. 在填筑和预压期，地表沉降的大、小变形分析结果的相对误差为2.86%~16.39%，而深度3.8 m处大、小变形分析结果的最大相对误差达20.23%，且大变形分析所得沉降量更接近于实测结果，说明对软土地基进行大应变分析很有必要。

c. 无论是大应变分析还是小应变分析，计算所得沉降量明显小于实测沉降量。造成这种差别的主要原因是室内试验所得参数难以完全准确地反映现场实际情况，表明要想获得合理、准确的数值模拟结果，必须寻求更加符合工程现场实际情况的计算参数^[20]。

6.2  水平位移

图4所示为路基坡脚外2.0 m，深度3.8 m附近的水平位移在路堤填筑及预压过程中的发展趋势。图5所示为填筑开始后，当t=605 d(预压接近结束)时在坡脚外2 m水平位移随深度的变化情况(其中，测斜管CX3-1和CX3-2的布置见图1)。从图4和图5可以看出：

a. 由大应变分析、小应变分析所得水平位移在加载初期(填土高度小于3.1 m时)差别很小，随着填筑高度增加，应力水平提高，大、小变形分析结果的差别愈来愈明显，这种差别甚至在预压期内仍有扩大。以深度3.8 m处为例，在施工及预压过程中，大、小应变分析结果的相对误差为3.02%~22.4%；

b. 大、小应变分析结果虽能较好地反映坡脚水平位移随施工进程的发展趋势，但有限元分析结果自始至终比实测水平位移大，这可能是计算参数与现场参数不同所致。

c. 有限元分析结果能很好地反映水平位移随深度的变化规律，大应变分析所得水平位移比小应变分析结果大。

d. 对深度9.5 m以下的亚黏土，由于土质较好，大、小应变分析结果的差别不大，605 d时的相对误差为10%~13.7%，但对上层软土，大、小应变分析结果的差别明显，605 d时相对误差为22.4%~27.8%，可见，对软土进行大应变分析很有必要。

1—测斜管CX3-1实测值, z=-4.0 m; 2—测斜管CX3-2实测值, z=-4.0 m; 3—小应变计算值, z=-3.8 m; 4—大应变计算值, z=-3.8 m

图4  深度3.8 m附近坡脚水平位移发展趋势

Fig.4  Development of horizontal displacement at toe of embankment with time at depth around 3.8 m

1—测斜管CX3-1实测值；2—测斜管CX3-2实测值；3—大应变计算值；4—小应变计算值

图5  t=605 d时坡脚水平位移随深度变化图

Fig.5  Relationship between horizontal displace and depth when t=605 d

6.3 孔隙水压力

图6所示为路基中心线下深度3.8 m处孔隙水压力计算值与深度4.5 m处实测值在路基施工过程中的发展趋势的对比结果。图7所示为路基中心线下深度7.7 m处孔隙水压力计算值与深度8.3 m处实测值的对比结果。

从图6和图7可以看出：有限元分析结果较好地反映了“薄层轮加法”填筑过程中孔隙水压力的多峰值现象，以及预压期孔隙水压力随时间逐步消散的趋势，但计算孔隙水压力的多峰值现象比实测值更加明显，且其峰值一般比实测值大；在整个施工过程中，大、小变形分析所得孔隙水压力的发展趋势一致，在t＜429 d时，其相对误差为2.05%~22.75%，此后，虽然计算分析的相对误差从数值上看似乎很大，但均在10 kPa以内；有限元分析结果与实测结果略有偏差，这种差别一方面源于计算中采用的土体水平和竖向渗透系数与现场实际情况存在差异，另一方面，也与某些孔隙水压力测点的测试精度不够高有关。

1—实测值；2—大应变计算值；3—小应变计算值

图6  深度4 m附近孔压计算值与实测值对比

Fig.6  Comparison of calculated pore water pressure with monitored ones around 4 m below ground surface

1—实测值；2—大应变计算值；3—小应变计算值

图7  深度8 m附近孔压计算值与实测值对比

Fig.7  Comparison of calculated pore water pressure with monitored ones around 8 m below ground surface

7  结  论

a. 大应变、小应变有限元分析所得地基沉降、水平位移、孔隙水压力等随施工进程的变化规律与实测沉降发展规律一致，说明本文建立的大应变粘弹塑性有限元分析方法是正确的。

b. 大、小应变分析结果的差异随应力水平的提高和时间的延长而上升，其地表沉降、地基沉降、水平位移和孔隙水压力的最大相对误差分别为16.39%，20.23%，27.8%和22.75%，说明对软土路基进行大应变分析很有必要。

c. 室内试验所得参数难以准确地反映现场实际情况，要想获得合理准确的数值模拟结果，必须寻求能够更加准确确定计算参数的方法。

参考文献：

[1] 魏丽敏, 何 群, 孙愚男. 砂井地基固结过程的监测与分析[J]. 中南大学学报: 自然科学版, 2004, 35(6): 1019-1024.
WEI Li-min, HE Qun, SUN Yu-nan. Measurement and analysis of consolidation process for sand drain ground[J]. Journal of Central South University: Science and Technology, 2004, 35(6): 1019-1024.

[2] 钱家欢, 殷宗泽. 土工原理与计算[M]. 北京: 中国水利水电出版社, 1996: 90-106.
QIAN Jia-huan, YIN Zong-ze. Principles and numerical methods of geotechnical engineering[M]. Beijing: China Water power Press, 1996: 90-106.

[3] 胡庆国, 阳军生, 黄生文. 采用泡沫聚苯乙烯修筑的轻型桥台路堤特性分析[J]. 中南大学学报: 自然科学版, 2006, 37(2): 408-413.
HU Qing-guo, YANG Jun-sheng, HUANG Sheng-wen. Analysis of performance of bridge approach embankment constructed by expanded polystyrene[J]. Journal of Central South University: Science and Technology, 2006, 37(2): 408-413.

[4] Cargill K W. Prediction of consolidation of very soft soil[J]. Journal of Geotechnical Engineering, 1984, 110(6): 775-795.

[5] Carte J P, Small J C, Booker J R. A theory of finite elastic consolidation[J]. International Journal Solids structures, 1977, 13(5): 467-478.

[6] Chopra M B, Dargush G F. Finite-element Analysis of time-dependent large-deformation problems[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1992, 16(2): 101-130.

[7] 朱 昊, 袁建新. 拖带坐标下的固结理论及其变分原理[J]. 岩土力学, 1990, 11(1): 11-17.
ZHU Hao, YUAN Jian-xin. Consolidation theory and its variational principle based on co-moving coordinate system[J]. Rock and Soil Mechanics, 1990, 11(1): 11-17.

[8] 周正明. 饱和土体大变形固结有限元分析[J]. 水利水运科学研究, 1992(1): 106-110.
ZHOU Zheng-ming. Large strain consolidation analysis for saturated soil[J]. Hydro-Science and Engineering, 1992(1): 106-110.

[9] 谢永利. 大变形固结理论及其有限元法[M]. 北京: 人民交通出版社, 1998: 1-25.
XIE Yong-li. Theory of large-strain consolidation and finite element analysis[M]. Beijing: ChinaCommunications Press, 1988: 1-25.

[10] 何君毅, 林祥都. 工程结构非线性问题的数值解法[M]. 北京: 国防工业出版社, 1994: 74-142.
HE Jun-yi, LIN Xiang-du. The numerical solutions of nonlinear problem in engineering structure[M]. Beijing: National Defence Industry Press, 1994: 74-142.

[11] 谢新宇. 一维大变形固结理论的研究[D]. 杭州: 浙江大学岩土工程研究所, 1996.
XIE Xin-yu. On the one-dimensional large strain deformation consolidation theories[D]. Hangzhou: Institute of Geotechnical Engineering, Zhejiang University, 1996.

[12] 蒋明镜, 沈珠江. 饱和软土的弹塑性大变形有限元平面固结分析[J]. 河海大学学报, 1998, 26(1): 73-77.
JIANG Ming-jing, SHEN Zhu-jiang. Finite element analysis of elasto-plastic large-strain consolidation for saturated cam-clay soft soils[J]. Journal of Hohai University, 1998, 26(1): 73-77.

[13] 张汝清, 詹先义. 非线性有限元分析[M]. 重庆: 重庆大学出版社, 1990: 101-141.
ZHANG Ru-qing, ZHAN Xian-yi. Nonlinear finite element analysis[M]. Chongqing: Chongqing University Press, 1990: 101-141.

[14] 王宏贵, 魏丽敏, 赫晓光. 根据长期单向压缩试验结果确定三维流变模型参数[J]. 岩土工程学报, 2006, 28(5): 669-673.
WANG Hong-gui, WEI Li-min, HE Xiao-guang. Determination of three-dimensional rheologic parameters based on long term oedometer test[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(5): 669-673.

[15] 魏丽敏. 软土路基双重非线性流-固耦合仿真分析与沉降预测[D]. 长沙: 中南大学土木建筑学院, 2005.
Wei Li-min. Double non-linear fluid-solid coupled simulating analysis and settlement prediction for soft soil subgrade[D]. Changsha: School of Civil and Architectural Engineering, Central South University, 2005.

[16] 孙 钧. 岩土材料流变及其工程应用[M]. 北京: 中国建筑工业出版社, 1999: 75-198.
SUN Jun. Rheology of geomaterial and its engineering application[M]. Beijing: ChinaArchitecture & Building Press, 1999: 75-198.

[17] 周德培. 流变力学原理及其在岩土工程中的应用[M]. 成都: 西南交通大学出版社, 1995: 1-71.
ZHOU De-pei. Rheology mechanics principle and its application in geotechnical engineering[M]. Chengdu: Southwest Jiaotong University Press, 1995: 1-71.

[18] Owen D R J, Hinton E. 塑性力学有限元——理论与应用[M]. 曾国平, 刘 忠, 徐家礼, 译. 北京: 兵器工业出版社, 1989: 112-405.
Owen D R J, Hinton E. Finite elements in plasticity theory and practice[M]. CEN Ping, LIU Zhong, XU Jia-li, trans. Beijing: China Weapon Industry Press, 1989: 112-405.

[19] 谢康和, 周 健. 岩土工程有限元分析理论与应用[M]. 北京: 科学出版社, 2002: 47-89.
XIE Kang-he, ZHOU Jian. Theory and application of finite elements method in geotechnical engineering[M]. Beijing: Science Press, 2002: 47-89.

[20] 魏丽敏, 何 群, 王永和. 软土参数反分析方法及其在沉降预测中的应用[J]. 中国铁道科学, 2007, 28(4): 1-6.
WEI Li-min, HE Qun, WANG Yong-he. Back-analysis method of soft soil parameters and its application in settlement prediction[J]. China Railway Science, 2007, 28(4): 1-6.

收稿日期：2008-02-25；修回日期：2008-05-25

基金项目：国家自然科学基金资助项目(50678177)；铁道部科技研究开发计划项目(2005K002-B-6)

通信作者：何  群(1969-)，男，江苏扬州人，博士，从事岩土工程教学与科研工作；电话：0731-2655063；E-mail: hequn@mail.csu.edu.cn