文章编号: 1004-0609(2005)07-1006-07
液-固挤压复合材料系统的模糊神经网络建模
齐乐华1, 史忠科2, 何俊超1, 李贺军3
(1. 西北工业大学 机电学院, 西安 710072;2. 西北工业大学 自动化学院, 西安710072;3. 西北工业大学 材料科学与工程学院, 西安 710072)
摘 要: 针对液-固挤压复合材料管、 棒材成形时工艺参数难于选取、 试验工作量大的问题, 在正交试验的基础上, 结合有限元模拟数据, 构建200组样本集, 将其中的150组作为训练样本用于网络的训练学习, 其余的50组作为测试样本用于验证网络的精确性。 通过对补偿模糊神经网络学习算法实现中的关键技术问题的处理, 如输入、 输出变量模糊集的划分、 模糊规则的提取、 学习速率的确定等, 基于模糊神经网络建立了液-固挤压复合材料工艺系统模型, 得到了浸渗时间与其它关键参数之间的映射关系及模糊规则, 利用该模型, 对关键工艺参数进行预测, 预测值与试验值吻合较好。 这为该工艺的实际应用和过程控制奠定了基础。
关键词: 模糊神经网络; 复合材料; 液-固挤压; 建模 中图分类号: TB18; TB331
文献标识码: A
Fuzzy neural network modeling of liquid-solid extrusion process for composite products
QI Le-hua1, SHI Zhong-ke2, HE Jun-chao1, LI He-jun3
(1. School of Mechatronic, Northwestern Polytechnical University, Xian 710072, China;
2. School of Automation, Northwestern Polytechnical University, Xian 710072, China;
3. School of Materials Science and Engineering, Northwestern Polytechnical University, Xian 710072, China)
Abstract: Liquid-solid extrusion process, as a method of forming tubes, bars from liquid metal in a single process, is a kind of new metal forming technology, which was developed in recent years. But there exist some problems for forming the composite tubes or bars by this process, such as the difficulty of selecting process parameters and large quantity of the experiments required. In order to deal with these existing problems, on the base of the orthogonal experiments and FEA simulation, 200 groups of samples are constructed (150 groups are used to train the network, and 50 groups are used to verify the network), and the system model for liquid-solid extrusion is established by the compensatory neurofuzzy network (CNFN). Many key techniques in the realization of CNFN learning algorithms, such as the distribution of fuzzy sets for input and output variables, the determination of fuzzy rules and learning rate, are solved. By the established model, the relation among the infiltration time and other parameters can be mapped, and the key process parameters for extruding composite bars are forecasted. The forecasted and experimental results are well matched. So the present work builds a foundation for the reasonable choosing of the process parameters and practical application of the liquid-solid extrusion.
Key words: neurofuzzy networks; composites; liquid-solid extrusion; modeling
液-固挤压复合材料工艺是近年来开发出的一种由液态金属直接成形复合材料管、 棒材的新工艺[1-3], 它克服了目前复合材料管、 棒材成形方法均需二次变形的弊端, 可以由液态金属直接成形出复合材料管、 棒材类制件, 其应用前景广阔[4]。 目前, 对于该工艺过程的力学建模、 数值模拟以及变形特征等方面已有报道[5-8], 但在工艺系统建模方面尚待深入研究。 由于该工艺是在金属处于半固态时进行挤压成形, 涉及液-固转变和大塑性变形, 影响因素较多, 是一复杂的非线性时变系统, 很难建立精确的数学模型。 模糊神经网络可以实现输入和输出向量的非线性映射, 并可从中提取推理规则, 建立系统模型, 进而进行非线性参数预测, 在模式识别、 过程控制、 系统建模与优化和参数预测等方面得到广泛应用[9-12]。 本文作者采用具有快速学习算法的补偿模糊神经网络[13]建立复合材料液-固挤压工艺系统模型, 并对关键工艺参数进行预测, 为该工艺的实际应用和过程优化控制奠定基础。
1 补偿模糊神经网络及其学习算法
补偿模糊神经网络具有6层结构: 输入层、 模糊化层、 模糊推理层、 补偿运算层、 反模糊化层和输出层。 层与层之间分别依据模糊变量、 模糊IF-THEN规则、 Min-Max运算、 模糊推理方法和反模糊化函数构建。 其学习过程实际上是调整输入输出隶属函数的中心和宽度的过程。
定义模糊子集Aki和Bki的模糊隶属函数:
式中a和σ为输入隶属函数的中心和宽度; b和δ为输出隶属函数的中心和宽度。
定义反模糊化函数f(x):
式中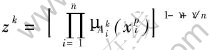
, γ为补偿度。
定义目标函数:
式中N为样本数量。
对于n维输入量xp, [xp=xp1, xp2, …, xpn]和一维输出量yp, p=1, 2, …, N, 根据梯度下降法, 可以得到输入、 输出隶属函数的中心和宽度a、 σ、 b、 δ以及补偿度γ(γ∈[0, 1])的训练公式:
式中η为学习率, t=1, 2, …。
2 模糊神经网络建模
利用模糊神经网络建立液-固挤压复合材料系统模型时, 需要确定输入、 输出参数以及各参数模糊集的个数、 模糊推理规则以及隶属函数等。 考虑到液-固挤压复合材料的成形特点, 影响变形过程的主要工艺参数有: 液态金属的浇注温度、 模具预热温度、 浸渗时间、 浸渗压力以及压制力等。 根据前期研究结果[14], 浸渗时间和压制力对复合材料成形过程影响较大, 且难于控制, 因而作为输出参数, 由此可以建立起这些参数与其它参数之间的映射关系, 以便进行参数预测与控制。 为了准确预测输出变量, 本文作者分别建立浸渗时间预测模型FNNT网络模型和变形力预测模型FNNP网络模型。 下面以FNNT模型的建立为例, 说明采用模糊神经网络建立液-固挤压复合材料系统的建模过程。
2.1 样本集的确定
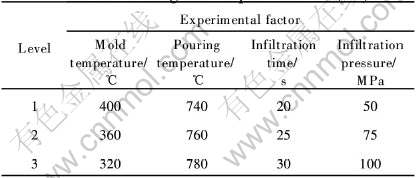
采用具有快速学习算法的补偿模糊神经网络建立系统模型, 首先需要通过大量试验以及专家经验建立样本集, 而后才能对模糊神经网络进行训练, 确定模型参数。 为了得到合理分布的训练样本, 本文采用正交实验法获取试验样本。 依据4因素(预热温度、 模具温度、 浸渗时间、 浸渗压力)、 3水平正交实验表L9(34) (表1)确定的参数组合, 在3150kN液压机上进行液-固挤压Al2O3sf/LY12短纤维增强铝基复合材料管、 棒材成形试验; 采用自行设计的数据采集系统记录试验数据, 包括模具温度、 浸渗压力、 浸渗时间、 位移和压制力等; 通过对正交试验数据的分析处理, 结合前期研究所积累的专家经验及有限元模拟数据[15], 选取200组数据组成样本集, 将其中的150组作为训练样本用于网络的训练学习, 其余的50组作为测试样本用于验证网络的精确性。
表1 液-固挤压复合材料正交试验L9(34)因素设定表
Table 1 Determination of factors and levels for orthogonal experiment L9(34)
2.2 模糊神经网络结构设计
2.2.1 模糊变量的设计
对于补偿模糊神经网络, 其模型结构是根据输入输出变量个数、 各变量的模糊集划分来确定的。 根据选定的工艺参数, 本文作者将FNNT模型确定为4输入(浇注温度θ1、 模具温度θ2、 变形力p1、 浸渗压力p2)、 单输出(浸渗时间t)的模糊神经网络模型。 考虑到模型的输入参数较多, 为控制模糊规则的数量和满足网络精度的要求, 将输入输出变量的模糊子集确定为3个。
按上述要求对输入、 输出变量进行模糊化处理, 每个输入变量有3个模糊子集, 即θ1、 θ2、 p1、 p2均为|NB, ZO, PB|, 表示其模糊论域中的负大、 适中、 正大, 其中θ1∈(680, 800), θ2∈(200, 400), p1∈(200, 520), p2∈(20, 120); 输出变量t=|NL, ZO, PL|, 表示模糊论域中的负长, 适中, 正长, t∈(15, 90)。 隶属函数选用高斯函数, 模糊集的具体划分见表2与表3。
2.2.2 模糊规则的提取
根据模糊变量的赋值情况及前期实验及理论研究, 初步确定81条模糊规则, 其中, 第i条模糊规则为:
R(i): IF θ1 is Ai1 and θ2 is Ai2 and p1 is Ai3 and p2 is Ai4 Then t is Bi (i=1, 2, 3, …, 81)(9)
式中 Aij (j=1, 2, 3, 4)表示输入变量的模糊子集, Bi表示输出变量的模糊子集。
确定模糊集以及模糊规则后, 便可依次对网络参数进行初始赋值。 由于液-固挤压复合材料的影响因素较多, 按前述研究构建的样本集不可避免地存在噪声, 因而初步确定的模糊规则还需要经过网络的学习训练去除噪声。 网络模型在学习过程中能够根据训练样本对网络参数进行动态调整, 直至达到期望精度, 从而提取出较为准确的模糊规则。
2.2.3 网络结构的确定
根据上述模糊变量、 模糊规则和隶属函数可以确定网络结构。 FNNT网络结构如图1所示。 网络第1层4个节点代表4个输入量: 浇注温度、 模具温度、 变形力以及浸渗压力; 网络第2层有12个节点, 代表4个输入量的所有模糊子集; 第3层有81个节点, 代表81条模糊规则; 第4层为网络补偿运算层; 第5层为解模糊层, 将模糊向量转变为精确向量; 第6层为输出向量层, 代表浸渗时间。
表2 FNNT网络输入参数模糊集划分
Table 2 Division of fuzzy set for input parameters of FNNT network
表3 FNNT网络输出参数模糊集划分
Table 3 Division of fuzzy set for output parameters of FNNT network
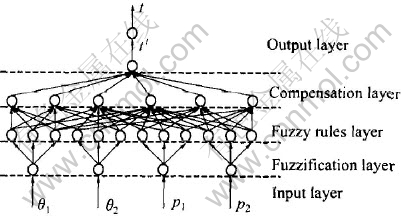
图1 FNNT网络模型结构图
Fig.1 Architecture of FNNT network
2.3 FNNT网络模型训练
2.3.1 网络参数调整
首先, 利用150组训练样本对FNNT网络进行训练, 逐渐对网络参数进行修正, 直至达到期望精度为止。 研究表明, 对网络参数赋予不同的初始值时, 网络达到期望精度需要进行的迭代次数也不尽相同。 如果网络参数的初始值接近实际情况, 网络需要迭代计算的次数相对较少, 否则需要较多次数的迭代计算。 由于补偿模糊神经网络参数均具有明确的物理含义, 因此可以通过对这些参数进行启 发式赋值, 以加快网络的学习速度。 表4所列为根据初始模糊规则对FNNT网络赋予的初值, 经过学习后的网络参数如表5所列。 显然, 从表5中可以得到输入量与输出量之间的映射关系。 实际上, 补偿模糊神经网络参数的物理意义即为工艺过程的推理规则, 其网络参数可以用规则的形式加以表达。 如表5可以表示为模糊规则形式:
R(1): IF θ1 is 713℃ and θ2 is 312℃ and p1 is 407MPa and p2 is 41.4MPa Then t is 47.7s;
R(2): IF θ1 is 720℃ and θ2 is 317℃ and p1 is 395MPa and p2 is 43.2MPa Then t is 27.7s
……(10)
通过上述规则, 可以较为直观地了解液-固挤压复合材料工艺的一般规律和实质性问题。
2.3.2 学习速率的影响
学习速率η对FNNT网络的收敛有较大影响。 表6和图2显示了η取值不同时对网络收敛情况的影响。 可以看出, η取小值时, 网络参数的修正幅度较小, 相应需要增加学习次数。 η取大值时, 参数修正幅度较大, 需要的训练次数相应较少。 到目前为止, η的选取主要是根据数值试验或经验来确定, 尚无完善的理论指导, 通常是尽可能取较大值, 这样可以加快网络的学习速度, 但要避免引起网络振荡。 一般情况下, 取值过大时, 容易引起网络振荡。 但从图2可以看出, 误差曲线几乎没有出现振荡现象, 且逐渐逼近收敛极限, 说明网络模型的稳定性较好。 η为0.10和0.01时, 收敛速度非常慢, 而η为0.80和0.98时, 收敛速度较快, 综合考虑收敛速度和模型精度, 本文中确定学习率η取值为0.98。
表4 FNNT网络初始参数
Table 4 Initial parameters of FNNT network
表5 训练后的FNNT网络参数
Table 5 Parameters after training of FNNT network
表6 学习速率η对收敛次数的影响
Table 6 Influence of learn speed on training epochs
图2 FNNT网络训练误差曲线
Fig.2 Error curves of FNNT training
2.3.3 网络模型训练
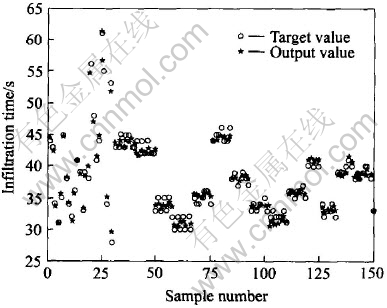
图3所示为FNNT网络训练时期望输出与实际输出的对比图。 可以看出, 网络的实际输出和期望输出的差值较小。 研究表明, 随着网络训练次数的增加, 网络的实际输出与期望输出之间的误差越来越小, 训练100次时的总误差为1.7809%, 单个样本最大绝对误差为4.243s, 最大相对误差为6.23%。 而训练次数达到200次时, 网络总误差减小为0.86%, 单个样本的最大误差为2.563s。 图3还表明, 误差较大的样本往往发生在样本稀疏的区域, 说明样本的合理选取对建模精度有较大影响, 因此, 应尽量使训练样本在其变量域内合理分布。
图3 FNNT网络训练输出值与目标值的比较
Fig.3 Comparison between output value and model target value of FNNT model
3 模型精度验证及讨论
网络模型性能评价采用
来进行。 其中, f(xp)为网络模型的输出, yp为期望输出, N为样本数。 利用50组测试样本对FNNT网络进行验证, 其输出值与期望值的对比情况见图4。 从图4中可以看出, 浸渗时间实际输出与期望输出值之间的最大相对误差为1.83%, 可以满足实际需要, 说明网络具有良好的泛化能力。
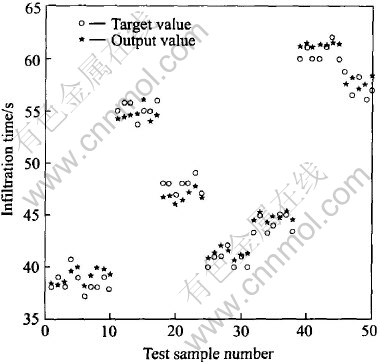
图4 浸渗时间预测模型验证图
Fig.4 Verification of model to redict infiltration-time
图5所示为浸渗时间与浇注温度及浸渗压力之间的耦合关系。 可以看出, 在浸渗压力不变的情况下, 浇注温度与浸渗时间的关系可以近似地认为是单调递增的, 随着浇注温度的升高, 相应需要的浸渗时间也就越长; 浸渗时间与浸渗压力的关系为一种近似抛物线的单调递增关系, 其总趋势为随浸渗压力的增加, 所需要的浸渗时间相应增长。 当浸渗压力为30MPa, 浇注温度为720℃时, 需要的浸渗时间最短; 而当浸渗压力为90MPa, 浇注温度为800℃时, 需要的浸渗时间最长。
图5 浸渗压力—浇注温度—浸渗时间关系
Fig.5 Relationship between infiltration pressure, pouring temperature and infiltration time
图6描述的是浸渗时间与模具温度及变形力之间的耦合关系。 浸渗时间与模具温度之间也是一种近似的单调递增关系, 随着模具温度的增高, 相应需要较长的浸渗时间。 从图6中还可以看出, 当模具温度为320℃, 变形力为295MPa时, 所需要的浸渗时间最短; 当模具温度为400℃, 变形力为500MPa时, 需要的浸渗时间最长。
图6 变形力—模具温度—浸渗时间关系
Fig.6 Relationship between deformation pressure, die temperature and infiltration time
从图5和图6还可以看出, 浸渗压力对浸渗时间的影响程度比浇注温度和模具温度的影响要小一些, 这与实验研究结果相吻合[3]。
按本文中所建立的FNNT模型中的参数及模糊规则指导试验, 取得良好效果, 说明所建立的模型是可行的。
4 结论
1) 基于补偿模糊神经网络建立了液-固挤压复合材料工艺系统模型, 得到了浸渗时间与其它关键参数之间的映射关系, 利用该模型, 可以对关键工艺参数进行预测, 预测值与试验值吻合较好。 为该工艺的实际应用和过程控制奠定了基础。
2) 提取的模糊规则对工艺试验具有指导意义。
REFERENCES
[1]HU Lian-xi, LUO Shou-jing, HUO Wen-can, et al. Development of the technique of extrusion directly following infiltration for the manufacturing of metal-matrix composites[J]. Journal of Materials Processing Technology, 1995(49): 287-294.
[2]齐乐华, 孙乐民, 侯俊杰, 等. 高效成形复合材料管、 棒材的新工艺研究[J]. 西北工业大学学报, 1999, 17(4): 629-632.
QI Le-hua, SUN Yue-ming, HOU Jun-jie. A new process for forming tube and bar products of composites without second forming[J]. Journal of Northwestern Polytechnical University, 1999, 17(4): 629-632.
[3]Qi L H, Li H J, Cui P L, et al. Forming of tubes and bars of alumina/LY12 composites by liquid extrusion process[J]. Trans Nonferrous Met Soc China, 2003, 13(4): 803-808.
[4]罗守靖, 田文彤, 李金平. 21世纪最具发展前景的近静成形技术—半固态加工[J]. 特种铸造及有色合金(压铸专刊), 2001, 7: 175-180.
LUO Shou-jing, TIAN Wen-tong, LI Jing-ping. The most promising near-net forming technology in 21 century—semi-solid processing[J]. Special Casting & Nonferrous Alloys, 2001, 7: 175-180.
[5]张广安, 罗守靖, 田文彤. 短碳纤维增强铝基复合材料的挤压浸渗工艺[J]. 中国有色金属学报, 2002, 12(3): 525-528.
ZHANG Guang-an, LUO Shou-jing, TIAN Wen-tong. Squeezing infiltration process for short carbon fiber reinforced aluminum alloy matrix composites[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(3): 525-528.
[6]齐乐华, 崔培玲, 史忠科, 等. 液-固挤压Al2O3sf/LY12复合材料管材成形过程的数值模拟[J]. 机械工程学报, 2002, 38(7): 102-106.
QI Le-hua, CUI Pei-ling, SHI Zhong-ke, et al. Numerical simulation on the liquid-solid extrusion process for forming Al2O3sf/LY12 composite tubes[J]. Chinese Journal of Mechanical Engineering, 2002, 38(7): 102-106.
[7]ZU Li-jun, LUO Shou-jing. Study on the power mixing and semi-solid extrusion forming process of SiCp/2024Al composites[J]. J Mater Proces Tech, 2001, 114: 189-193.
[8]HU Lian-xi, LUO Shou-jing, HUO Wen-can. Determination of the threshold pressure for infiltration of liquid aluminum into alumina short fiber preform[J]. Trans Nonferrous Met Soc China, 1996, 6(4): 133-137.
[9]Park M W, Park B T, Kim S K, et al. Incremental supervised learning of cutting conditions using the fuzzy ARTMAP neural network[J]. Annals of the CIRP, 2000, 49(1): 375.
[10]Gurkan E, Erkmen I. Two-way fuzzy adaptive identification and control of a flexible-joint robot arm[J]. Information Sciences, 2002(145): 13-43.
[11]Chungchoo C, Saini D. On-line tool wear estimation in CNC turning operations using FNN model[J]. Machine Tools & Manufacture, 2002(42): 29-40.
[12]Liao G C, Tsao T P. Application of fuzzy neural networks and artificial intelligence for load forecasting[J]. Electric Power Systems Research, 2004, 70: 237-244.
[13]Zhang Y Q, Kandel A. Compensatory neurofuzzy systems with fast learning algorithms[J]. IEEE Transactions on Neural Networks, 1998, 9(1): 83-105.
[14]齐乐华, 史忠科, 侯俊杰, 等. 复合材料棒材半固态挤压工艺参数的神经网络预测方法[J]. 塑性工程学报, 2003, 10(1): 20-24.
QI Le-hua, SHI Zhong-ke, HOU Jun-jie. Neural network forecasting method of process parameters for forming composite bar products by semi-solid state extrusion[J]. Journal of Plasticity Engineering, 2003, 10(1): 20-24.
[15]Qi L H, Shi Z K, Li H J, et al. Simulation of liquid infiltration and semi-solid extrusion for composite tubes by quasi-coupling thermal-mechanical finite element method[J]. Journal of Materials Science, 2003, 38(17): 3669-3675.
基金项目: 国家自然科学基金资助项目(50175091); 国防预研基金资助项目; 西北工业大学博士论文创新基金资助项目
收稿日期: 2004-12-23; 修订日期: 2005-04-21
作者简介: 齐乐华(1957-), 女, 教授, 博士.
通讯作者: 齐乐华, 教授; 电话: 029-88460447; 传真: 029-88491982; E-mail: lihejun@nwpu.edu.cn
(编辑 杨兵)
