采用元胞自动机结合Laasraoui-Jonas位错密度模型模拟AZ31镁合金的动态再结晶行为
来源期刊:中国有色金属学报(英文版)2013年第9期
论文作者:刘 筱 李落星 何凤亿 周 佳 朱必武 张立强
文章页码:2692 - 2699
关键词:AZ31镁合金;动态再结晶;微观组织;模拟
Key words:AZ31 magnesium alloy; dynamic recrystallization; microstructure; simulation
摘 要:采用元胞自动机结合Laasraoui-Jonas 位错密度模型(LJ模型)模拟AZ31镁合金在动态再结晶过程中的位错密度和微观组织演化。LJ模型中的硬化参数、回复参数和应变速率灵敏系数决定模拟的准确性。在目前的研究中,基于LJ模型和Kocks-Mecking模型(KM 模型)求解硬化参数;采用动态再结晶中的稳态应力公式求解回复参数和应变速率灵敏系数。结果表明:模拟结果与实验结果一致。
Abstract: The dynamic recrystallization (DRX) process of AZ31 magnesium alloy including microstructure and dislocation density evolution during hot compression was simulated by adopting the cellular automaton (CA) method coupling the Laasraoui-Jonas model (LJ model). The reliability of simulation depended on the accuracy of the hardening parameter, the recovery parameter and the strain rate sensitivity in the LJ model. The hardening parameter was calculated in terms of the LJ model and the Kocks-Mecking model (KM model), and then the recovery parameter and the strain rate sensitivity were obtained by using the equation of steady state flow stress for DRX. Good agreements between the simulations and the experimental observations were achieved.
Trans. Nonferrous Met. Soc. China 23(2013) 2692-2699
Xiao LIU1,2, Luo-xing LI1,2, Feng-yi HE1,2, Jia ZHOU1,2, Bi-wu ZHU1,2, Li-qiang ZHANG1,3
1. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha 410082, China;
2. College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China;
3. College of Mechanical and Electrical Engineering, Central South University of Forestry and Technology, Changsha 410004, China
Received 25 July 2012; accepted 1 February 2013
Abstract: The dynamic recrystallization (DRX) process of AZ31 magnesium alloy including microstructure and dislocation density evolution during hot compression was simulated by adopting the cellular automaton (CA) method coupling the Laasraoui-Jonas model (LJ model). The reliability of simulation depended on the accuracy of the hardening parameter, the recovery parameter and the strain rate sensitivity in the LJ model. The hardening parameter was calculated in terms of the LJ model and the Kocks-Mecking model (KM model), and then the recovery parameter and the strain rate sensitivity were obtained by using the equation of steady state flow stress for DRX. Good agreements between the simulations and the experimental observations were achieved.
Key words: AZ31 magnesium alloy; dynamic recrystallization; microstructure; simulation
1 Introduction
High stacking fault energy metals (SFE), such as aluminum, betas titanium alloys, and ferritic steels, undergo dynamic recovery (DRV) rather than dynamic recrystallization (DRX) during hot deformation. But for low- and medium- stacking fault energy metals, such as magnesium alloy, copper, nickel, and austenitic steel, DRX occurs during hot deformation [1-5].
The main characteristics of DRX may be summarized as follows: 1) A critical value of dislocation density is required for onset of DRX; 2) The recrystallized grains (R-grains) are equiaxed and the average grain size stays same at a given deformation condition; 3) Preexistent grain boundaries (GBs) are usually nucleation sites [6-8].
Since it is difficult to study the microstructural evolution characteristics during grain growth by physical experiments, computer simulations have been used by many researchers [9]. Up to now, various approaches have been proposed to simulate DRX, such as the Monte Carlo (MC) method and the cellular automaton (CA) method. The MC method has been widely adopted to study microstructural evolution, for instance, normal grain growth, grain growth with second-phase particles, and recrystallization [10]. Several researchers [8,11] used a MC method to study DRX in detail, including the prediction of the transition from single to multi-peak flow curves, the effect of initial grain size and the peak strain dependence on peak stress, as well as the dependence of steady state grain size on steady state stress. However, grain growth kinetics during DRX was not simulated by these simulations, due to the limitations of the MC method. The CA method is algorithm that represents discrete spatial and temporal evolution of complex systems by applying local or global deterministic or probabilistic transformation rules to the location of a lattice. The system objects are quantified according to generalized state variables [1]. GOETZ and SEETHARAMAN [12] first attempted to simulate DRX by the CA method. This method did not consider the hot-deformation parameters (e.g. temperature and strain rate), their effects on DRX process (e.g. nucleation, volume fraction and average dynamically R-grain sizes), and the relationship between the nucleation sites and the dislocation density distribution. Compared with the MC method simulations, the CA method is also probabilistic, but relatively flexible in simulating different physical systems and effective in calculation [6].
Dislocation density plays a very significant role in nucleation and microstructural evolution of DRX during hot deformation [1]. Therefore, many models have been attempted to describe the evolution of dislocation density, such as the LJ model [13], the KM model [14], and the two-parameter model [15]. These models, which are internal variable dislocation density models, aim to calculate the flow stress and the evolution of dislocation density during hot deformation process. However, the modified LJ model, which was proposed by GOURDET and MONTHEULLET [2], considers the influence of GB migration on dislocation density. Thus, the modified LJ model has provided a more realistic description of the evolution of dislocation density. Meantime, our previous research [16] has proved that the LJ model is suitable to simulate the dislocation density evolution in detail, and has successfully used the modified LJ model to simulate the microstructural evolution of Mg-Al-Ca-based alloy during hot extrusion.
In this work, the hardening parameter was firstly obtained based on the LJ model and the KM model. The recovery parameter and the strain rate sensitivity were obtained by adopting the equation of steady state flow stress for DRX based on the hardening parameter. Then, the CA method combining the LJ model was adopted to simulate the DRX process of AZ31 magnesium alloy under different temperatures and strain rates. The relation between the nucleation sites and the dislocation distribution and the relationship among critical strain, critical dislocation density and DRX were studied. By comparing with the experimental results, the simulated results were also validated.
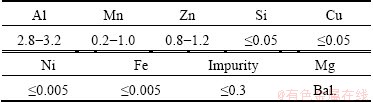
2 Experimental
Hot compression tests were performed on a Gleeble-3500 machine to obtain the stress—strain curves over five temperatures ( 300, 350, 400, 450 and 500 °C) with five strain rates (0.03, 0.3, 3, 30 and 90 s-1) and a strain of 1 to calculate material constants. These material constants were used in simulations. Cylindrical specimens of AZ31 magnesium alloy with a diameter of 10 mm and a height of 12 mm were machined with the compression axis parallel to the extruded solid bar axis. The chemical composition is given in Table 1. To study the microstructure of AZ31 magnesium, the cross- sections parallel to compression axis were cut from the deformed specimens and those samples were mounted, polished and etched. The average grain size from the experimental microstructure was calculated by using the Jeffries’s procedure mentioned in the ASTM standard test method [17]. The average grain size for the simulations was calculated by the simulated program.
Table 1 Main chemical composition of AZ31 magnesium alloy (mass fraction, %)
3 Modeling
3.1 Dislocation density model
From a microscopic point of view, concurrent phenomena, which are work hardening (WH), DRV, and DRX, are responsible for the evolution of dislocation density during hot compression. In order to describe the evolution of dislocation density inside crystallites during DRX, the modified LJ model was adopted. The equation can be expressed as
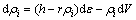 (1)
(1)
where ρi is the dislocation density of the ith grain; ε is the strain; dV is the volume swept by mobile boundaries; h is the average strain hardening parameter; r is the recovery coefficient parameter.
In order to accurately calculate the value of parameters in the LJ model, the KM model was used:
 (2)
(2)
where dε=dt represents the strain increment; 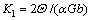 is a constant that describes the WH; α is a constant of 0.5-1; G is the shear modulus; b is the Burger’s vector;
is a constant that describes the WH; α is a constant of 0.5-1; G is the shear modulus; b is the Burger’s vector; 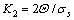 is the softening parameter that represents recovery of dislocation; σs is the steady stress;
is the softening parameter that represents recovery of dislocation; σs is the steady stress;  is the work hardening rate (see section 4.2.1).
is the work hardening rate (see section 4.2.1).
3.2 Model of DRX nucleation and growth
There are several nucleation models for DRX. QIAN and GUO [1], considering that the nucleation rate is linearly proportional to strain rate, proposed the following equation:
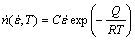 (3)
(3)
where 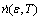 is the nucleation rate; Q is the activation energy which can be obtained by flow curves; C is a constant. The equation shows that the nucleation rate increases with temperature and strain rate.
is the nucleation rate; Q is the activation energy which can be obtained by flow curves; C is a constant. The equation shows that the nucleation rate increases with temperature and strain rate.
In moderate to low stacking fault energy metals, DRX occurs only when dislocation density reaches the critical value. ROBERTS and AHLBLOM [8] proposed a critical dislocation density ρc for the nucleation of DRX on the pre-existing grain boundary by bulging mechanism after considering the free energy change [18].
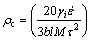 (4)
(4)
where τ is the dislocation line energy; l is the free path of dislocation; M is the GB mobility [18,19]; γi is the GB energy, which can be calculated by the Read-Shockley [9] equation and can be represented as follows:
 (5)
(5)
where θi is the misorientation between the ith R-grain and its neighboring grain. The GB energy of high angle boundary can be written as follows:
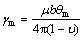 (6)
(6)
where γm and θm are the boundary energy and the misorientation when the GB becomes a high angle boundary, respectively; υ is the Poisson ratio.
The velocity of GB movement is the result of the net pressure on the boundary, which can be written as
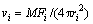 (7)
(7)
where vi is the velocity of GB; Fi is the driving force [20]; ri is the radius of the ith R-grain.
3.3 Cellular automaton method and procedures of simulation
In this method, the simulated area was set to correspond to the experimental microstructure area. Each lattice has four variables: one orientation variable that represents the grain orientation and determines the grain boundary energy which is calculated by Eqs. (5) and (6); one statues variable that indicates which is the R-grains; one dislocation density variable that determines the site energy and is calculated by Eq. (1); one color variable that exhibits the different grains. The orientations of primary matrix and R-grains were randomly set to 0°-180°. For new R-grains, the dislocation density was preliminarily set to zero. When the dislocation density exceeds the critical dislocation density calculated by Eq. (4), the DRX is initiated. Then the nucleation number can be obtained by Eq. (3) in each time step. For the growth of R-grain, when the driving force for the growth of the ith R-grain is positive, this R-grain can continuously grow until the driving force reaches zero, and the growth velocity vi in each time step is determined by Eq. (7). The volume swept by the grain boundary for the ith R-grain during each time step can be calculated according to the radius of the ith R-grain. Then, the dislocation density evolution can be calculated by Eq. (1) in each time step. The calculation was terminated, while the pre-set strain was reached.
The lattices in which recovery happens are random [11]. Then, an algorithm involvement of selection of a certain number of lattices Nr for recovery occurrence during each time step was selected as follows:
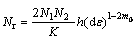 (8)
(8)
where N1 is the number of rows in lattices; N2 is the number of columns in lattices; K is the material constant [11]. The material parameters for simulation are shown in Table 2.
Table 2 Materials parameters of AZ31 magnesium alloy

4 Results and discussion
4.1 Experimental results
The flow curves which were obtained from the hot compression tests are shown in Fig. 1. It can be seen that the flow curves consist of four stages: the work hardening stage, the transition stage, the softening stage, and the steady stage for the combined influence of WH, DRV and DRX [23]. All the flow curves show a single peak, implying the occurrence of DRX during hot compression [19,24].
4.2 Calculation of WH rate 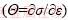 and constitutive parameters
and constitutive parameters
4.2.1 WH rate
The WH rate 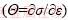 can be calculated from the slope of true stress—strain curves in the WH stage. The critical strain (εc), the peak stress (σp), and the saturated stress (σsat) can be gotten from the WH rate curves [25,26] (see Fig. 2).
can be calculated from the slope of true stress—strain curves in the WH stage. The critical strain (εc), the peak stress (σp), and the saturated stress (σsat) can be gotten from the WH rate curves [25,26] (see Fig. 2).
According to KM model, it is assumed that Θ is a function of deformation strain rate and temperature, which can be expressed as follows:
 (9)
(9)
where the constants A1 and m1 can be derived by one-dimensional linear regression analysis after taking the natural logarithm of both sides (see Fig. 3).
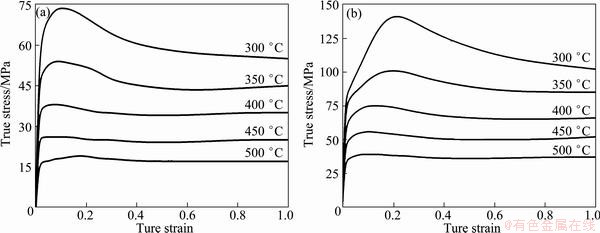
Fig. 1 True stress—strain curves for AZ31magnesium alloy at strain rates of 0.03 s-1 (a) and 3 s-1 (b) under various temperatures with a strain of 1
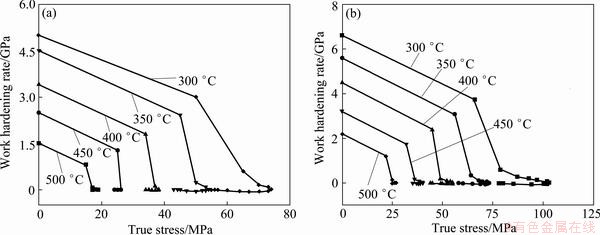
Fig. 2 Work hardening rate—true stress curves for AZ31 magnesium alloy at strain rate of 0.03 s-1 (a) and 3 s-1 (b) under various temperatures with a strain of 1
4.2.2 Hardening parameter
The first terms of the KM model (h) and the LJ model (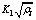 ) are used to describe the creation and accumulation of dislocations. Hence, the strain hardening parameter in the LJ model can be written as the following equation:
) are used to describe the creation and accumulation of dislocations. Hence, the strain hardening parameter in the LJ model can be written as the following equation:
 (10)
(10)
where ρ0 is the average initial dislocation density.
4.2.3 Recovery parameter
Under any conditions, the flow stress is proportional to the square root of dislocation density, and can be written as [5,7,13]
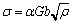 (11)
(11)
During steady state, the flow stress is a function of deformation strain rate and temperature, and can be expressed as the following constitutive equation [3]:
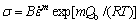 (12)
(12)
The average strain hardening parameter h and the recovery coefficient parameter r can be written as the following expressions [3]:
 (13)
(13)
 (14)
(14)
where 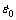 =1; ε is the strain rate; the recovery parameter r0 (in Eq. (14)) and the hardening parameter h0 (in Eq. (13)) are constant; m is the strain rate sensitivity; Qb is the activation energy for self-diffusion; R is the gas constant; T is the thermodynamic temperature.
=1; ε is the strain rate; the recovery parameter r0 (in Eq. (14)) and the hardening parameter h0 (in Eq. (13)) are constant; m is the strain rate sensitivity; Qb is the activation energy for self-diffusion; R is the gas constant; T is the thermodynamic temperature.
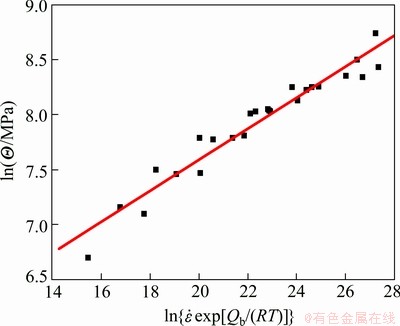
Fig. 3 Relationship between lnΘ and 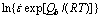
Equation (12) is used to match the data at ε=1 when B is constant. If GB migration effects are overlooked, Eq. (1) yields ρ=hi/r in the steady state. Then the steady state stress can be derived by combining Eqs. (11), (13) and (14):
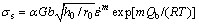 (15)
(15)
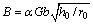 (16)
(16)
The constants m (in Eq. (15)) and B (in Eq. (16)) can be calculated by one-dimensional linear regression analysis after taking the natural logarithm of both sides (see Fig. 4).
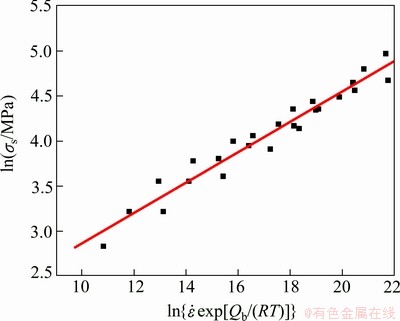
Fig. 4 Relationship between lnσs and 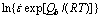 under all conditions
under all conditions
Based on the equations mentioned above, the hardening parameter, the recovery parameter and the strain rate sensitivity are determined. The results can be expressed as the following equations:
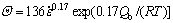 (17)
(17)
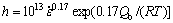 (18)
(18)
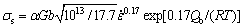 (19)
(19)
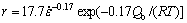 (20)
(20)
4.3 Simulation results and discussion
In order to analyze microstructural and dislocation density evolution of AZ31 magnesium alloy, the CA method coupling the LJ model was employed. The simulated microstructure and dislocation density evolution during DRX for AZ31 magnesium alloy were carried out using the actual experimental parameters, and were compared with experimental results.
The simulations of microstructural and dislocation density evolution with strain changing, which were carried out at 500 °C with a strain rate of 0.03 s-1, are illustrated in Fig. 5. The simulated microstructures are shown in Figs. 5(a1), (b1) and (c1). The different colors show different grains and the black lines represent grain boundaries. The corresponding simulated dislocation densities are shown in the Figs. 5(a2), (b2) and (c2), respectively. The white color shows ρi=0, the black color corresponds to the existence of dislocation, and the higher dislocation density is represented by darker color. As deformation proceeds, the dislocation density must exceed a critical value for initiation of DRX. New grains begin to grow, but the concurrent working hardening creates dislocation density inside them and reduces the driving force for GB migration until the growth stops [5]. When the strain approaches to 0.1186 (εc=0.1186), the simulated result shows that some new grains start emerging (Fig. 5 (a1)), and the dislocation density inside the new grains becomes zero (Fig.5 (a2)). It is shown that the dislocation density evolution is accurately calculated by the LJ model. Therefore, it is validated that the parameters in the LJ model are correct. From the comparison between the simulated microstructure and the corresponding dislocation density distribution, it is shown that the white color regions in Figs. 5 (a2), (b2) and (c2) are associated with the sites of nucleation in Figs. 5 (a1), (b1) and (c1), respectively.
The comparison between the simulated microstructure and the experimental grain structure at a strain rate of 0.03 s-1 under a temperature of 400 °C and a strain of 1 are shown in Fig. 6. Compared with the grain structure at a strain rate of 0.3 s-1 under the same temperature and strain (Fig. 7), the grain size is refined, as a result of the DRX nucleation rate increasing with strain rate (in Eq. (5)). Compared Fig. 6 with the microstructure under a temperature of 500 °C with a strain rate of 0.03 s-1 and a strain of 1 (Fig. 8), the grain size at high temperature is much bigger, due to the higher velocity of GB migration. After comparing the simulated results with the experimental observations, some discrepancies can be observed (Figs. 6, 7 and 8), because of the possible involvement of additive high energy sites for nucleation which has not been taken into account during simulation, such as dislocation tangle and dislocation pining. In general, the simulated results agree well with the experimental findings.
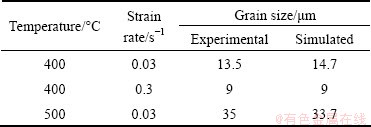
It is shown that the simulations of final grain size are in quantitative agreement with the experimental results in Table 3.

Fig. 5 Prediction of microstructure at strain of 0.1186 (critical strain) (a1), 0.6 (b1) and 1 (c1), and corresponding simulated dislocation density (a2), (b2) and (c2), respectively, at 500 °C with a strain rate of 0.03 s-1

Fig. 6 Comparison between simulated microstructure (a) and experimental observation (b) at strain rate of 0.03 s-1, temperature of 400 °C and strain of 1

Fig. 7 Comparison between simulated microstructure (a) and experimental observation (b) at strain rate of 0.3 s-1, temperature of 400 °C and strain of 1

Fig. 8 Comparison between simulated microstructure (a) and experimental observation (b) at strain rate of 0.03 s-1, temperature of 500 °C and strain of 1
Table 3 Comparison of final grain size by CA model with experimental data
5 Conclusions
1) The hardening parameter, which was calculated based on the LJ model and the KM model, was obtained to be 1013 m-2. The recovery parameter and the strain rate sensitivity were calculated by using the relationship between flow stress and strain rate at steady state during DRX, and were gotten the values of 17.7 and 0.17, respectively.
2) Using the CA method coupling the LJ model to simulate DRX during hot compression, the models for DRX and the value of parameters in the LJ model were verified.
3) It was verified that the nucleation locations of R-grains had strong link to dislocation density distribution during DRX. The critical strain and dislocation density for the onset of DRX, the variation of mean grain size with temperature and strain rate, and the final mean grain size agree well with the experimental measurements.
References
[1] QIAN M, GOU Z X. Cellular automata simulation of microstructural evolution during dynamic recrystallization of an HY-100 steel [J]. Materials Science and Engineering A, 2004, 365(1-2): 180-185.
[2] GOURDET S, MONTHEULLET F. A model of continuous dynamic recrystallization [J]. Acta Materialia, 2003, 51(9): 2685-2699.
[3] GOURDET S, MONTHEILLET F. Effects of dynamic grain boundary migration during the hot compression of high stacking fault energy metals [J]. Acta Materialia, 2002, 50(11): 2801-2812.
[4] XIAO N M, ZHENG C W, LI D Z, LI Y Y. A simulation of dynamic recrystallization by coupling a cellular automaton method with a topology deformation technique [J]. Computer Materials Science, 2008, 41(3): 366-374.
[5] KUGLER G, TURK R. Modeling the dynamic recrystallization under multi-stage hot deformation [J]. Acta Materialia, 2004, 52(15): 4659-4668.
[6] XIAO H, XIE H B, YAN Y H, JUN Y G. Simulation of dynamic recrystallization using cellular automaton method [J]. Journal of Iron and Steel Research International, 2004, 11(2): 42-45.
[7] DING R, GUO Z X. Coupled quantitative simulation of microstructure evolution and plastic flow during dynamic recrystallization [J]. Acta Materialia, 2001, 49(16): 3163-3175.
[8] ROBERTS W, AHLBLOM B. A nucleation criterion for dynamic recrystallization during hot working [J]. Acta Metallurgica, 1978, 26(5): 801-813.
[9] SHELTON R K, DUAND D C. Computer modeling of particle pushing and clustering during matrix crystallization [J]. Acta Materialia, 1996, 44(11): 4571-4585.
[10] HE Y Z, DING H L, LIU L F, SHIN K. Computer simulation of 2D grain growth using a cellular automata model based on the lowest energy principle [J]. Materials Science and Engineering A, 2006, 429(1-2): 236-246.
[11] PECKZAK P, LUTON M J. A Monte Carlo study of the influence of dynamic recovery on dynamic recrystallization [J]. Acta Metallurgica, 1993, 41(1): 59-71.
[12] GOETZ R L, SEETHARAMAN V. Modeling dynamic recrystallization using cellular automata [J]. Scripta Materialia, 1998, 38(3): 405-413.
[13] LAASRAOUI A, JONAS J J. Prediction of steel flow stresses at high temperatures and strain rates [J]. Metallurgical and Materials Transactions A, 1991, 22(7): 1545-1558.
[14] MECKING H, KOCKS U F. Kinetics of flow and strain-hardening [J]. Acta Materialia, 1981, 29(11): 1865-1875.
[15] ESTRIN Y, KUBIN L P. Local strain hardening and nonuniformity of plastic deformation [J]. Acta Metallurgic, 1986, 34(12): 2455-2464.
[16] LI L X, HE F Y, LIU X, LOU Y, ZHOU J, DUCZCZYK J. Simulation of the grain structure evolution of a Mg-Al-Ca-based alloy during hot extrusion using the cellular automation method [J]. Key Engineering and Materials, 2012, 491: 264-272.
[17] ASTM E112-96∈. Standard test method for determining average grain size [S].
[18] FROST H J, ASHBY M F. Deformation-mechanism maps: The plasticity and creep of metal and ceramics [M]. Oxford: Pergamon Press, 1982: 44.
[19] SAKAI T. Dynamic recrystallization microstructures under hot working conditions [J]. Journal of Materials Processing Technology, 1995, 53(1-2): 549-561.
[20] READ W T. Dislocation in crystal [M]. New York: McGraw Hill, 1953: 181.
[21] KNEZEVIC M, LEVINSON A, HARRIS R, MISHRA K R, DOHERTY D R, KALIDINAI R S. Deformation twinning in AZ31: Influence on strain hardening and texture evolution [J]. Acta Materialia, 2010, 58(19): 6230-6242.
[22] KITAZONO K, SATO E, KURIBAYASHI K. Internal stress superplasticity in polycrystalline AZ31 magnesium alloy [J]. Script Materialia, 2001, 44: 2695-2702.
[23] CHEN F, CUI Z S, LIU J, ZHANG X X, CHEN W. Modeling and simulation on dynamic recrystallization of 30Cr2Ni4MoV rotor steel using the cellular automation method [J]. Modeling Simulation in Materials Science and Engineering, 2009, 17: 1-19.
[24] XIN R L, WANG B S, ZHOU Z, HUANG G J, LIU Q. Effect of strain rate and temperature on microstructure and texture for AZ31 during uniaxial compression [J]. Transactions of Nonferrous Metals Society of China, 2010, 20: s594-s598.
[25] POLIAK E I, JONAS J J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization [J]. Acta Materialia, 1996, 44(1): 127-136.
[26] McQUEEN H J, CELLIERS O C. An application of hot workability studies to extrusion processing [J]. Canadian Metallurgical Quarterly, 1996, 35(4): 305-19.
刘 筱1,2,李落星1,2,何凤亿1,2,周 佳1,2,朱必武1,2,张立强1,3
1. 湖南大学 汽车车身先进设计制造国家重点实验室,长沙 410082;
2. 湖南大学 机械与运载工程学院,长沙 410082;
3. 中南林业科技大学 机电工程学院,长沙 410004
摘 要:采用元胞自动机结合Laasraoui-Jonas 位错密度模型(LJ模型)模拟AZ31镁合金在动态再结晶过程中的位错密度和微观组织演化。LJ模型中的硬化参数、回复参数和应变速率灵敏系数决定模拟的准确性。在目前的研究中,基于LJ模型和Kocks-Mecking模型(KM 模型)求解硬化参数;采用动态再结晶中的稳态应力公式求解回复参数和应变速率灵敏系数。结果表明:模拟结果与实验结果一致。
关键词:AZ31镁合金;动态再结晶;微观组织;模拟
(Edited by Hua YANG)
Foundation item: Project (51075132) supported by the National Natural Science Foundation of China; Project (2010DFB70180) supported by the Program of International Science & Technology Cooperation; Project (2011BAG03B02) supported by the National Key Technology R&D Program during the 12th Five-Year Plan Period of China
Corresponding author: Luo-xing LI; Tel/Fax: +86-731-88821950; E-mail: luoxing_li@yahoo.com
DOI: 10.1016/S1003-6326(13)62786-7

