射流冲击下矩形柱鳍热沉结构优化
涂福炳,武荟芬,周孑民,曾文辉,刘亮,贾煜
(中南大学 能源科学与工程学院,湖南 长沙,410083)
摘要:采用实验与数值计算相结合的方法对空气射流冲击下的矩形柱鳍热沉的肋片结构进行优化研究。对不同肋高和肋宽的矩形柱鳍热沉的热阻进行实验研究,并选用标准的k-ε湍流模型进行数值计算分析。研究结果表明:热阻随喷口雷诺数Re或喷口高径比H/D的增大而减小,但Re或H/D增大到一定程度时,热阻减小的幅度就不再明显;当热沉肋高范围为0.3≤Hf/L≤0.42、肋片宽度为Df/L=0.1时,热沉的散热能力与散热经济性之间能达到较好的平衡。将模拟结果与实验结果进行比较,相对误差在10%以内。
关键词:空气冲击射流;矩形柱鳍热沉;热阻;数值模拟;肋片优化
中图分类号:TK12;TP391.9 文献标志码:A 文章编号:1672-7207(2012)03-1171-08
Optimization of rectangular pin fin heat sinks during air jet impingement
TU Fu-bing, WU Hui-fen, ZHOU Jie-min, ZENG Wen-hui, LIU-liang, JIA-yu
(School of Energy Science and Engineering, Central South University, Changsha 410083, China)
Abstract: The experimental and numerical method was done in the process of optimization of rectangular pin fin heat sink. The thermal resistance of a series of rectangular pin fin heat sinks with different fin height and width was experimented and calculated by the k-ε model. The results show that the thermal resistance decreases as Renolds number (Re) and nozzle height-diameter ratio (H/D) increase, but this tend becomes less obvious as Re and H/D increase to some extent.When fin height scope of heat sink is between 15 and 21 mm, the balance of cooling ability and economical efficiency are reached. Comparing the simulation results with the experimental results, the correlated error does not exceed 10%.
Key words: air jet impingement; rectangular pin fin heat sink; thermal resistance; numerical simulation; fin optimazation
冲击射流广泛应用于印刷电路板制造业、印刷工业、食品制造业、飞机机翼除冰、透平机械中迎流叶片的冷却、玻璃制造业以及电子元件、计算机芯片的冷却等工业过程中[1-2]。Tuckerman和Pease[3]在20世纪80年代提出了微通道热沉冷却概念。此后,对多种热沉如将空气冲击射流与平板鳍片热沉[4-7]、多孔介质热沉[8]或方形柱鳍热沉[9-11]结合起来进行了传热特性实验研究。结果表明,与光滑表面时的情况相比,加装热沉后的散热能力要高2.8~9.7倍。而最高肋高的热沉仅仅比中等肋高热沉的散热能力稍强一点。当高径比(通过改变喷口与热沉间距)从1~5变化时,散热能力的变化并不明显。近年来,数值方法已应用到对冲击射流与热沉结合散热的研究过程中。文献[12-15]研究结果表明:数值计算获得的热阻与实验值相吻合。同时,对热沉的肋高及肋片横截面积的优化研究还说明,肋片尺寸的变化能引起热沉散热性能较大的变化。
在热沉的结构优化方面,通过计算最小的热沉热阻而不是肋片的最大传热量来获得最优热沉结构。在国内,陈希章等[16]利用空气冲击射流,对2种不同的散热器的性能进行了测试, 分析了散热器的稳态、瞬态下的储热和散热性能,从而探索了散热器性能评价方法及标准的散热性能测试方法。吴慧英等[17]对集成微热沉系统进行了设计和开发。研究了将冷却微通道、微型测温元件以及微型发热元件集成在同一张单晶硅片上的设计和制作方法。综上所述,国外对柱鳍热沉的研究一般具有高Re、大射流孔径及多选择规则外形热沉(如方形柱鳍热沉)的特点。国内对于冲击射流的研究,起步较晚,对于空气冲击射流换热方面的数值研究及实验研究较少。因此,应进一步加强空气射流冲击下热沉的基础性研究,加深对其流动本质和传热特性的认识;同时加大热沉的工程应用研究,如将空气射流与热沉结合应用于芯片冷却等。因此,本文作者采用实验与数值计算相结合的方法对空气射流冲击下的矩形柱鳍热沉的肋片结构进行优化研究,具有一定的理论意义和工程应用价值。
1 数学模型及边界条件
1.1 控制方程
在对空气射流冲击热沉散热的数值模拟过程中,假设:
(1) 气体为不可压缩流。
(2) 忽略流体浮升力作用。
(3) 忽略辐射传热。
(4) 常物性参数条件。
采用雷诺时均方法,假设流动参数表示成如下形式:
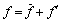 (1)
(1)
其中: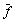 为平均分量;
为平均分量; 为脉动分量,则连续性方程及动量方程可写成如下形式:
为脉动分量,则连续性方程及动量方程可写成如下形式:
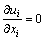 (2)
(2)
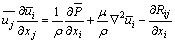 (3)
(3)
其中: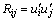 为雷诺应力。
为雷诺应力。
采用波辛涅斯克假设(Boussinesq hypothesis)来关联雷诺应力和平均速度梯度,如下式:
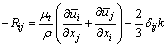 (4)
(4)
式中: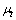 为湍流黏度;
为湍流黏度;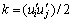 为湍动能;
为湍动能;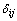 为单位张量,i=j时,取值1,i≠j时取值0。
为单位张量,i=j时,取值1,i≠j时取值0。
对于湍流流动,存在下述关系:
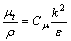 (5)
(5)
其中:ε为能量耗散率,经验常数Cμ取值为0.09。
于是,引入2个来评定湍流度及能量耗散率的方程来使控制方程组封闭,其形式分别如下:
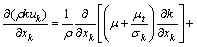
 (6)
(6)
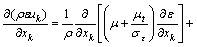
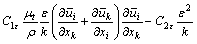 (7)
(7)
式中:ρ为密度,kg/m3;μ为动力黏度。模型常数的取值为:C1ε=1.44,C2ε=1.92,σk=1.0,σε=1.3。
对于能量方程,可以分成2个部分来进行考虑。在热沉内部,热量以导热的方式传递,其能量方程的形式如下:
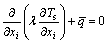 (8)
(8)
式中:λ为热沉热导率,W/(m K);Ts为热沉内部温度,℃;
K);Ts为热沉内部温度,℃;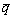 为模拟芯片的单位体积的热产率,W/V3。
为模拟芯片的单位体积的热产率,W/V3。
在热沉外部的流体流动区域,热量以对流方式传递,其能量方程的形式为:
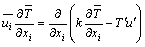 (9)
(9)
1.2 边界条件的确定
对热沉的壁面作如下假设:
(1) 所有速度分量为0,即壁面无滑移边界条件。
(2) 导热及对流传递的能量守恒。
边界条件如下:
(1) 速度入口,将喷口设为速度入口边界。喷口直径定为4 mm,入口速度则为33.2 m/s(此时对应的Re为9 478),流体入口温度尽量与实验条件相符。
(2) 射流板和射流板设为圆形,直径为30 mm,在其中心即为射流喷口。射流板对射流具有一定的限制作用。在数值模拟中,将射流板设置为绝热面。
(3) 发热面,发热面即为模拟芯片表面,将其上表面设为等热流边界。给定热流密度与实验条件一致,选用20 W作为冲击射流实验中的加载功率。
(4) 压力出口,将流体出口表压设为0,即出口处为大气压。流体出口温度为大气温度。根据文献[15],取湍流度为5%,回流温度因为对换热影响不大,将其设为与入口温度相同。
1.3 柱鳍热沉结构尺寸
在研究过程中,选用的热沉结构如图1所示,热沉的具体参数如表1所示。
1.4 解析区域的确定
在对空气射流冲击热沉散热的数值模拟研究过程中,采用三维模型。由于热沉结构上的特点,使得散热模型存在左右、前后对称的特点,因此,选择其1/4模型来进行数值研究。此外,由于将压力出口边界条件设为大气压,应适当将计算区域向热沉外部空间扩展,即压力出口适当外移,此时的出口压力将更符合假设。
边界条件的设置如图2所示,图2(a)和2(b)分别表示了数值模型行向及列向中心对称面上边界条件。
采用流体仿真软件Fluent 6.0对上述数学模型进行计算,在网格划分的过程中,采用TGrid方法将整个计算区域划分为Tet/Hbrid网格形式。其中,热沉部分的网格密度为1,流体空间部分的网格密度为2.5。此外,对入口处的面网格进行了加密处理,最后所得网格总数一般不少于105。
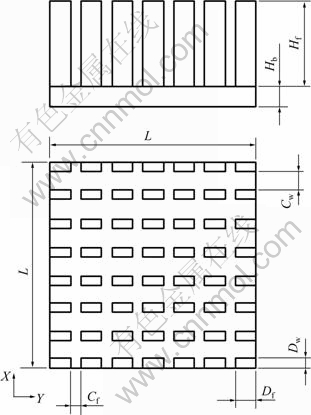
图1 矩形肋片的柱鳍热沉结构图
Fig.1 Structure drawing of rectangular pin fin heat sink
表1 矩形肋片的柱鳍热沉结构参数
Table 1 Structural parameters of rectangular pin fin heat sinks
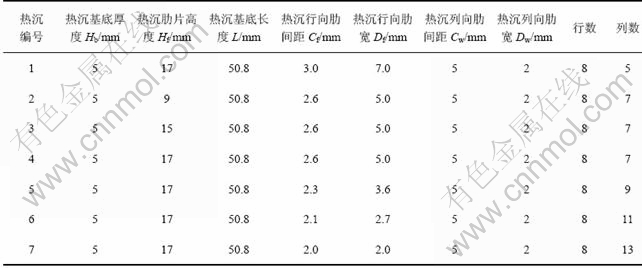
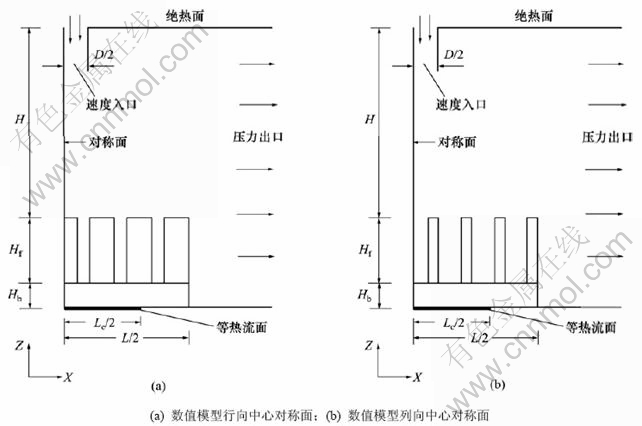
图2 边界条件设置
Fig.2 Boundary condition
2 肋片高度优化
2.1 实验原理及系统
热量从芯片内部散发出来,通过热沉的热传导再散发到空气中,最后由空气冲击射流将热量带走。这就是空气冲击射流作用于柱鳍热沉进行散热的基本过程。其中,封装元件与热沉之间的填充物是导热硅胶,它起着连接加固及导热作用。其原理如图3所示。实验系统的结构简图如图4所示。
2.2 实验结果与模型验证
热沉热阻θab是反映热沉散热性能的一个重要指标,也是设计新型热沉或改进热沉结构时必需的一个重要参数。
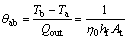 (10)
(10)
其中:Ta和Tb分别为环境温度和热沉底部温度,℃;Qout为通过热沉由空气冲击射流带走的热量,W;η0为热沉肋片的总散热效率;hf为热沉表面传热系数,W/(m2 K);At为热沉总散热表面积,m2。
K);At为热沉总散热表面积,m2。
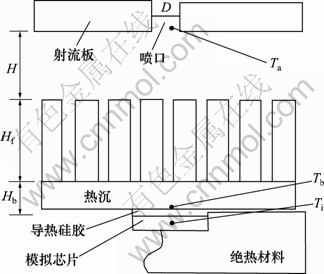
图3 实验原理示意图
Fig.3 Experiment principle
在肋片高度优化实验研究过程中,选用2,3和4号3个热沉除了肋片高度分别为9,15及17 mm的差别外,其构造完全相同。
空气射流的雷诺数为Re=UD/ 。式中:U为流体通过喷口时的流速,m/s;
。式中:U为流体通过喷口时的流速,m/s; 为空气的运动黏度,m2/s。
为空气的运动黏度,m2/s。
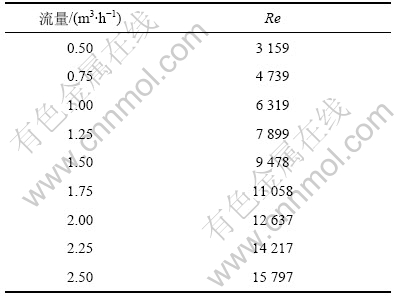
在实验过程中,对Re的改变是通过调节流量计改变空气流量来实现的,Re与空气流量的对应关系见表2。

图4 实验系统
Fig.4 Experiment system
表2 Re与空气流量的对应关系
Table 2 Relation of Re and air flux
在Re=9 478,H/D=10的条件下,分别对2号、3号、4号热沉及其他2个肋高为21 mm和27 mm的热沉进行数值模拟计算,并与同一条件下的实验结果进行比较,如图5所示。
从图5可以看出:热阻随着肋高的增大而减少,但是热阻减小的幅度却趋于缓慢。当肋高由21 mm增大到27 mm时,热沉的热阻由1.08 ℃/W变为1.01 ℃/W,变化并不明显,即散热能力并没有显著的增加;而将肋高从9 mm增大到15 mm时,热沉的热阻由1.55 ℃/W变为1.15 ℃/W,其散热能力的增大的幅度明显要大的多。因此,尽管热沉的高度越大,其热阻会越低,但是,当其高度到达一定程度时,再增大肋片高度,其热阻减小的幅度甚至可以忽略不计。反而会使得空间加大,成本增加而得不偿失。
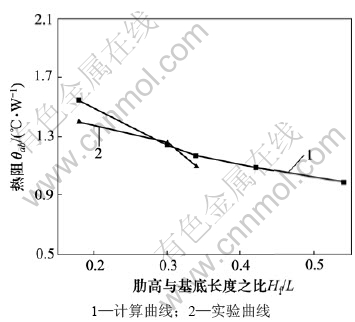
图5 热阻随Hf/L的变化
Fig.5 Variation of thermal resistance to Hf/L
从图5可知:2号(Hf /L=0.18)、3号(Hf /L=0.30)及4号(Hf /L=0.34)热沉热阻的实验值与计算值均较为接近。其中,2号热沉热阻的实验值和计算值的相对误差不超过10%,3号及4号热沉的热阻的实验值和计算值尤为接近,它们的相对误差均不超过5%,这说明标准的k-ε湍流模型是可行的。
2.3 数值计算结果及分析
利用控制方程对不同肋高热沉进行数值计算,其列向中心对称面的温度分布如图6~8所示。从图6~8可知:2号热沉(Hf=9 mm)内部的温度分布最为均匀,等温线最为密集,温度梯度较大,说明2号热沉的散热能力还有较大提高的可能。而肋高Hf=27 mm的热沉内部的温度分布最不均匀,其等温线层次较为分明,接近热源部分的等温线呈圆形对称分布。在冲击区,其顶部与底部之间的温度差较为明显,且越接近肋片顶部,等温线之间的间隔也就越大。因此,若再增加肋片高度,其散热能力的增加已不再明显。数值计算结果显示,3号热沉(Hf=15 mm)和肋高Hf=21 mm的热沉数值计算得出的结果是一样的,2个热沉的散热表现正好处在这两者之间。

图6 Re=9 478, H/D=10时, 2号热沉(Hf=9 mm)列向中心对称面的温度分布
Fig.6 Temperature distribution of No.2 heat sink (Hf=9 mm) on center symmetry plane as Re=9 478, H/D=10

图7 Re=9 478, H/D=10时, 3号热沉(Hf=15 mm)及热沉Hf=21 mm列向中心对称面的温度分布
Fig.7 Temperature distribution of No.3 heat sink (Hf=15 mm) and heat sink (Hf=21 mm) on center symmetry plane as Re=9 478, H/D=10
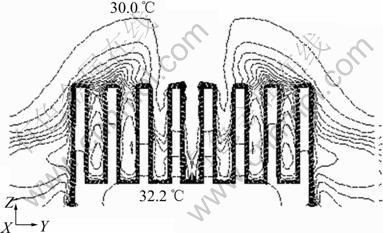
图8 Re=9 478, H/D=10时,Hf=27 mm热沉列向中心对称面的温度分布
Fig.8 Temperature distribution of heat sink (Hf=27 mm) on center symmetry plane as Re=9 478, H/D=10
在热沉肋高的结构优化设计中,首先要满足芯片的散热及安全性方面的要求,其次才考虑热沉散热经济性的要求。根据实验和计算结果,在空气射流与热沉结合散热的应用中,建议热沉肋高取值范围为0.3≤Hf/L≤0.42。在此区间,热沉的散热能力与散热经济性之间能达到一个较好的平衡。
3 肋片宽度优化
3.1 数值计算结果
在Re=9 478, H/D=10时,4号热沉及7号热沉的列向中心对称面的温度分布如图9和10所示,4号热沉及7号热沉的列向中心对称面的速度矢量如图11和12所示。由图11和12可以看出:7号热沉在空气射流冲击下的最大温差比4号热沉的大,说明4号热沉的散热效果好于7号热沉。同时7号热沉的温度较高区域较4号热沉有明显的上移现象。
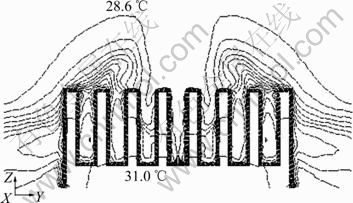
图9 Re=9 478, H/D=10时,4号热沉列向中心对称面的温度分布
Fig.9 Temperature distribution of No.4 heat sink on center symmetry plane as Re=9 478, H/D=10

图10 Re=9 478, H/D=10时,7号热沉列向中心对称面的温度分布
Fig.10 Temperature distribution of No.7 heat sink on center symmetry plane as Re=9 478, H/D=10
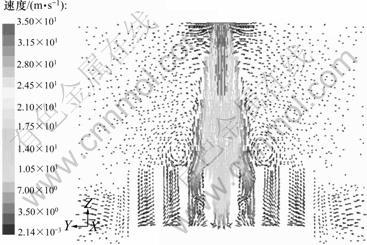
图11 Re=9 478, H/D=10时,4号热沉列向中心对称面的速度矢量
Fig.11 Velocity distribution of No.4 heat sink on center symmetry plane as Re=9 478, H/D=10
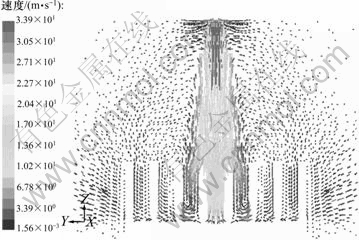
图12 Re=9 478, H/D=10时,7号热沉列向中心对称面的速度矢量
Fig.12 Velocity distribution of No.7 heat sink on center symmetry plane as Re=9 478, H/D=10
通过研究发现,其原因是由于4号热沉的空气射流大部分从肋片底部散发到大气空间中,而7号热沉则由于流体受到较大阻力而向上发展造成空气射流在其肋片顶部有相当大的分布。另外,4号热沉在其肋片上部有较明显的漩涡,且更靠近射流核心。这也是4号热沉的散热效果要好于7号热沉的原因之一。
3.2 实验结果
热沉肋片宽度的改变必然引起其散热表面积以及冲击射流的流动方式的改变,这样也就必然引起热沉散热能力的改变。在固定热沉肋片厚度的条件下,以确定热沉肋片的最优宽度为研究目标。
在实验过程中,选用了1号、4号、5号、6号及7号5个热沉,结构参数见表1。这些热沉肋宽与基底长度比Df/L分别为0.14,0.1,0.072,0.054和0.04,热沉的肋片行数为8、肋高为17 mm,肋片列数则分别为5,7,9,11及13不等。
将这5个热沉在3组不同实验条件下的热阻进行比较,如图13所示。
从图13可以看出:热沉的热阻均随Re数或H/D的增大而减少。4号热沉的热阻最小,7号热沉的热阻最大。也就是说4号热沉的具有最优的散热效果,而7号热沉的散热效果最差。实验结果验证了仿真结果的正确性。
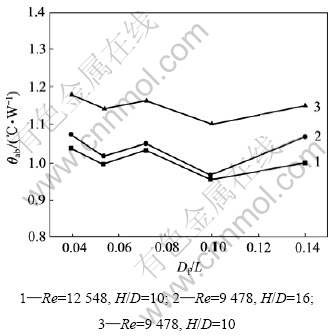
图13 不同肋片宽度的热沉的热阻比较
Fig.13 Thermal resistance comparison of different fin heat sinks
4 结论
(1) 热沉热阻随喷口雷诺数Re或喷口高径比H/D的增大而减小,但当Re或H/D增大到一定程度时,热阻减小的幅度就不再明显。
(2) 热沉较优的肋片高度范围为0.3≤Hf/L≤ 0.42,在此区间,热沉的散热能力与散热经济性之间能达到一个较好的平衡。
(3) 在固定热沉肋片厚度的条件下,热沉肋宽与基底长度比Df/L=0.1时,热沉具有最优的散热效果。
(4) 肋片高度优化试验中,数值模拟结果与实验结果比较,相对误差小于10%。
参考文献:
[1] Mahajan R, Nair R, Wakharkar V, et al. Emerging directions for packaging technologies[J]. Intel Technology Journal, 2002(2): 61-74.
[2] 李腾, 刘静. 芯片冷却技术的最新研究进展及其评价[J]. 制冷学报, 2004, 25(3): 22-32.
LI Teng, LIU Jing. Latest research advancement and assessment of chip cooling techniques[J]. Journal of Refrigeration, 2004, 25(3): 22-32.
[3] Tuckerman D B, Pease R F W. High-performance heat sinking for VLSI[J]. IEEE Electron Device Letters, 1981, EDL-2(5): 126-129.
[4] YU Xiao-ling, FENG Jian-mei, FENG Quan-ke, et al. Development of a plate-pin fin heat sink and its performance comparisons with a plate fin heat sink[J]. Applied Thermal Engineering, 2005, 25(2/3): 173-182.
[5] DUAN Zhi-peng, Muzychka Y S. Impingement air cooled plate fin heat sinks. PartⅠ: Pressure drop model[C]//Proceedings of the Ninth Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems. 2004: 429-435.
[6] DUAN Zhi-peng, Muzychka Y S. Impingement air cooled plate fin heat sinks. Part Ⅱ: Thermal resistance model[C]//Proceedings of the Ninth Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems. 2004: 436-443.
[7] Sasao K, Hanma M, Nishihara A, et al. Numerical analysis of impinging air flow and heat transfer in plate fin type heat sinks[J]. Transactions of the ASME. Journal of Electronic Packaging, 2001, 123(3): 315-318.
[8] TZENG Sheng-chung, MA Wei-ping. Experimental investigation of heat transfer in sintered porous heat sink[J]. International Communications in Heat and Mass Transfer, 2004, 31(6): 827-836.
[9] Hansen L G, Webb B W. Air jet impingement heat transfer from modified surfaces[J]. International Journal of Heat and Mass Transfer, 1993, 36(4): 989-997.
[10] El-Sheikh H A, Garimella S V. Enhancement of air jet impingement heat transfer using pin-fin heat sinks[J]. IEEE Transaction on Component and Packaging Technology, 2000, 23(2): 300-308.
[11] El-Sheikh H A, Garimella S V. Heat transfer from pin-fin heat sinks under multiple impinging jets[J]. IEEE Transaction on Advanced Packaging, 2000, 23(1): 113-120.
[12] Reddy A V. Experimental and numerical study of heat sinks with impingement flow at high Reynolds numbers[C]//Proceedings of Nineteenth Annual IEEE Semiconductor Thermal Measurement and Management Symposium. 2003: 176-178.
[13] Jung H H, Maveety J G. Pin fin heat sink modeling and characterization[C]//Proceedings of Sixteenth Annual IEEE Semiconductor Thermal Measurement and Management Symposium. 2000: 260-265.
[14] Maveety J G, Jung H H. Design of an optimal Pin-fin heat sink with air impingement cooling[J]. International Communications in Heat and Mass Transfer, 2000, 27(2): 229-240.
[15] Maveety J G, Jung H H. Heat transfer from square pin-fin heat sinks using air impingement cooling[J]. IEEE Transactions on Components and Packaging Technologies, 2002, 25(3): 459-469.
[16] 陈希章, 刘中良, 马重芳, 等. 电子芯片散热特性的测试研究[J]. 工程热物理学报, 2004, 25(6): 995-997.
CHEN Xi-zhang, LIU Zhong-liang, MA Chong-fang, et al. An experimental study of the performance and the characteristic of heat sinks of electronic chips[J]. Journal of Engineering Thermophysics, 2004, 25(6): 995-997.
[17] 吴慧英, 郑平. 集成微热沉系统的设计和制作[J]. 微细加工技术, 2004(1): 52-57.
WU Hui-ying, ZHENG Ping. Design and fabrication of integrated micro-heat sink[J]. Microfabrication Technology, 2004(1): 52-57.
(编辑 陈爱华)
收稿日期:2011-04-25;修回日期:2011-06-20
基金项目:国家自然科学基金资助项目(50376076)
通信作者:涂福炳(1966-),男,湖南邵阳人,博士,副教授,从事热工设备过程仿真、工业节能技术研究;电话:13908439589;E-mail: tfbone@163.com