DOI：10.19476/j.ysxb.1004.0609.2019.10.16

波导管弯曲工艺参数对壁厚减薄量的影响

胡福泰，汪飞雪，臧新良，彭加耕

(燕山大学 机械工程学院，秦皇岛 066004)

摘  要：本文建立了波导管弯曲分析有限元分析模型，针对6063波导管计算了不同弯曲半径下过渡区域壁厚分布，利用稳定变形区壁厚简化计算公式，得到稳定变形壁厚与弯曲半径关系曲线。对给定波导管(内腔15.8 mm×7.9 mm，壁厚1.0 mm)计算了不同弯曲角度下(ρ=40 mm)弯曲外侧壁厚分布，指出小半径弯曲过渡区域可以延伸到30°范围甚至更大。取90°弯曲件进行了壁厚计算值与实验值比较，除去两端10°内急剧变化段，壁厚减薄率误差小于2%。通过对比变形过渡区弧长，确定弯曲过渡区中性层弧长稳定在管材宽度B的1.2倍左右，并依此给出简化的壁厚计算公式。通过计算得出芯棒支撑范围应与过渡变形区范围一致，小半径弯曲时可达到30°角度范围。文中分析了顶推力、摩擦因数、芯棒支撑角度等对壁厚变化的影响规律，并给出了合理计算结果。这些分析计算对指导波导管弯曲研究和生产技术改进提供了重要依据。

关键词：波导管弯曲；弯曲工艺；壁厚减薄；变形区

文章编号：1004-0609(2019)-10-2348-08　     中图分类号：TG355.7　　     文献标志码：A

由于管材弯曲件具有结构合理、外形美观、强度高、缺陷少、性能优等突出特性，其应用越来越广泛^[1]，但是管材弯曲件的利用也常常受到弯曲成形技术上的制约，如起皱、开裂、断面畸变严重、壁厚过度减薄等是各类专家关注的焦点。根据管材弯曲件的具体用途和要求，人们研究出各种弯曲方法。

管材弯曲看似简单，实际上有多种成形工艺参数对弯曲结果产生影响，其中主要有弯曲力与力矩、顶推力、管材夹紧力、弯曲变形角度、弯曲半径、模具间隙、模具结构、摩擦与润滑、芯棒形式与参数、管材参数及材料等。这些参数组合变化，相互影响，相互制约，大大增加了研究难度。目前，学者们大多针对不同管材规格来研究探索弯曲变形的成形极限^[1]。

近年来，迅速发展起来的数控弯管技术为高效精密弯曲成形创造了条件，但这些新技术的应用离不开对弯曲机理的深入研究，而薄壁厚(t＜1.5 mm)和小弯曲半径(相对弯曲半径ρ与管径d的比值小于2)的产品，常常会出现一些技术困难需要学者们去解决^[2-3]。

TANG^[4]利用最大剪应力理论和塑性流动理论分析了圆管弯曲过程，给出弯曲壁厚变化、截面变化率，中性轴偏移量、弯曲力矩、断面形状改变等解析计算公式。这些公式在推导过程中使用大量简化和假设，虽精度不高，但对指导生产实际有一定实用价值。STACHOWICZ^[5]考虑轴向助推，理论推导了扁化因子和中性层移动量的解析式，分析了助推作用对弯矩和弯管壁厚的影响。LAZARESCU^[6]通过有限元模拟和实验验证研究内部充液压力对铝合金圆管断面畸变和壁厚扁化的影响。MILLER等^[7]实验研究了铝合金矩形管拉弯成形过程中，张紧力、侧压力、摩擦力对管材断面畸变、回弹及轴向伸长的影响。哈尔滨工业大学尹承禹^[8]研究了22MnB5特定材料矩形管绕弯弯曲成形极限。西北工业大学杨合等^[9-11]实验研究了薄壁圆管绕弯成形壁厚减薄和断面畸变规律。刘郁丽等^[12-13]运用ABAQUS仿真软件，针对矩形管采用铰链式芯棒绕弯成形，对起皱波形、断面畸变、壁厚变化、回弹量等进行了研究，给出特定管材断面变形和壁厚减薄变化曲线。但上述研究和分析很难直接应用到不同芯棒结构的波导管弯曲中。

由于波导管弯曲要求断面变形小于2%(用户通过实测提出)，接近断面形状不改变，工艺难度很大，研究波导管弯曲机理、工装结构和工艺参数分布规律，对完善和丰富高端管材弯曲技术有重要意义。本文利用ANSYS软件，对6063波导管弯曲工艺进行了模拟分析，得出了多种工艺参数对矩形波导管弯曲壁厚变化影响的一些规律，这对于提高波导管弯曲质量和今后进一步研究新弯曲工艺有重要指导作用。

1  计算模型及基本参数

根据弹塑性理论，在有限元分析软件ANSYS中建立了矩形波导管绕弯的简化分析模型^[14]，模型中充分考虑了芯棒和顶推力的作用。芯棒形式如图1(a)所示，支撑角度为30°，管坯内腔与芯棒之间无间隙，摩擦因数设为0.01；夹紧块与管坯间无相对运动，接触刚度为1。有限元分析模型如图1(b)所示。

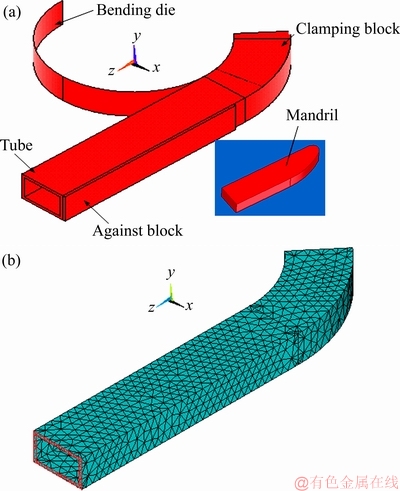
图1  有限元分析实体模型与网格划分

Fig. 1  Finite element analysis model(a) and grid(b)

管材是6063铝合金，矩形波导管绕弯变形情况及相关参数见图2。其中，ρ为不考虑中性层内移的弯曲半径，R为管材弯曲内侧曲率半径；管坯尺寸：内腔宽H，内腔高E，管材壁厚T，外形宽B（B= H+2T)为17.8 mm，高(E+2T)为9.9 mm，壁厚(T)为1 mm。其他符号：E₁为弯曲后弯曲外侧高度，E₂为弯曲后弯曲内侧高度，T₁为弯曲后外侧壁厚，T₂为弯曲后内侧壁厚。顶推力加在整个管坯后端面上，大小为170 N。图2中α角度范围内的管材外侧壁减薄和内侧壁增厚均已达到稳定状态，维持相对稳定的数值，这部分区域称为已变形区或变形稳定区；变形稳定区的两端到管材直段范围，均称为过渡区，靠近弯曲起始端的过渡区称为已变形过渡区，而靠近弯曲结束端的过渡区称为变形区或变形过渡区。本文假设两端的过渡区完全相同。

6063铝合金是AL-Mg-Si系中具有中等强度的可热处理强化合金，Mg和Si是主要合金元素，本文仅研究成品6063铝合金波导管在塑性弯曲时的变形规律及工艺参数对壁厚变化的影响。图3所示为经过软化处理的6063波导管材料特性曲线。

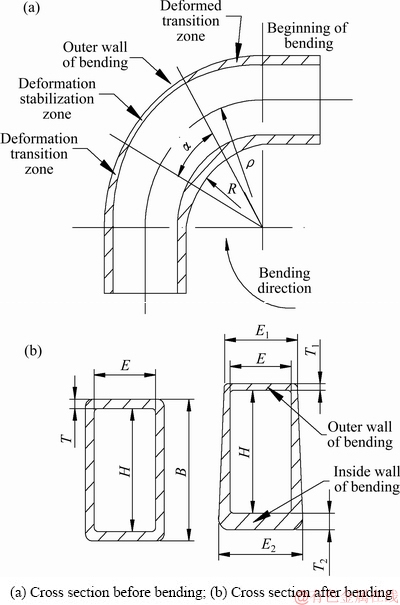
图2  波导管弯曲变形示意图

Fig. 2  Schematic diagram of waveguide bending deformation

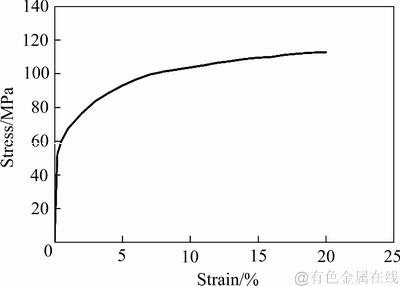
图3  6063波导管材料特性实验曲线

Fig. 3  Material characteristic curve of 6060 waveguide

2  弯曲半径对壁厚减薄的影响

分别取弯曲半径为40、80和100 mm，弯曲角度取90°进行计算，弯曲外侧壁壁厚分布如图4所示。

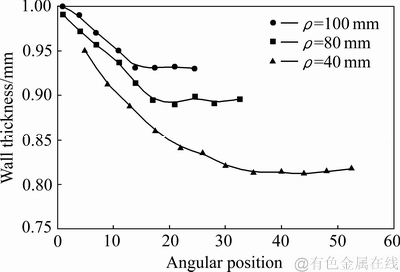
图4  弯曲外侧壁过渡区壁厚沿弯曲弧角度分布

Fig. 4  Thickness distribution of taper zone outer wall of bend along angular positions

从图4中可以看出，管材外侧壁厚度变化从弯曲起始点开始减薄，直至最大减薄点出现前，维持近似线性分布，达到最大减薄率后基本维持稳定变形。弯曲半径不同，代表弯曲变形程度不同，弯曲半径ρ值越小，管材变形程度越大，壁厚减薄越快，图4中壁厚变化曲线与垂直方向坐标轴的夹角数值越小。实践经验及本文后续分析均清楚表明，弯曲半径ρ对壁厚减薄的影响起决定作用，而顶推力、摩擦因数、芯棒支撑位置、管材相对壁厚等对壁厚减薄的影响均在2%~3%左右徘徊，这是由于波导管弯曲的工艺条件要求苛刻造成的，受起皱、开裂、断面畸变制约，使得工艺参数变化范围受到严重限制。相匹配的工艺参数得到的成形结果非常接近。因此有可能通过简化的方法预测弯曲成形后管材外侧壁的壁厚。

管材弯曲达到稳定阶段壁厚值后，按照上述理念,弯曲中性层内移特性与轴向顶推作用的中性层外移特性相抵消，因此可采用式(1)和(2)简化算法计算^[15]。

                            (1)

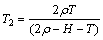                            (2)

由式(1)取H=15.8，T=1，可以得出弯曲达到稳定变形的最小壁厚T₁、最大壁厚T₂与弯曲半径ρ的曲线对应关系如图5所示。

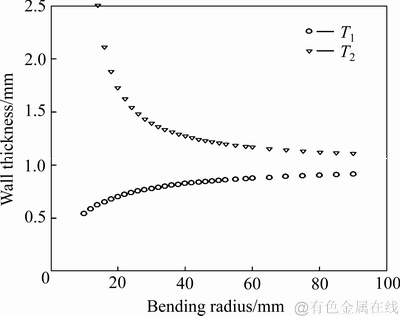
图5  弯曲半径与理论壁厚对应曲线

Fig. 5  Bending radii and corresponding theoretical wall thickness

由图5可见，对于给定管材(内腔15.8 mm×7.9 mm，壁厚1.0 mm)，弯曲半径ρ取值为25~40之间时，管材壁厚存在剧烈变化区，此时管件极易发生变形集中，引起外壁破裂。制作小R管件时应采用小摩擦力芯棒同时合理施加轴向压力，以防止外侧壁在弯曲时破裂。

3  弯曲角度对管壁减薄的影响

3.1  弯曲角度的影响

通常人们认为弯曲变形过渡区域很小，弯曲壁厚减薄量只与弯曲变形程度有关，与弯曲角度无关。常规的计算管材弯曲最小壁厚与最大壁厚的表达式中也没有弯曲角度变量。但事实上，通过图4的壁厚随弯曲角度的分布可以看出，弯曲变形的过渡区域，当弯曲半径较小时可以延伸到很大范围，对本文给定的管材(内腔15.8 mm×7.9 mm，壁厚1.0 mm)当弯曲半径ρ取40 mm时，弯曲过渡区域可以延伸到30°范围，而且此过渡区域有两段，弯曲起始段和弯曲结束段。因此，有必要研究管材弯曲过渡区域壁厚变化规律。

图6描述的是弯曲曲率半径ρ=40 mm时，不同弯曲角度(用θ表示，θ指管件弯曲弧线所对应的圆心角角度)的管件，其管材外侧壁减薄量与角度位置的对应关系。

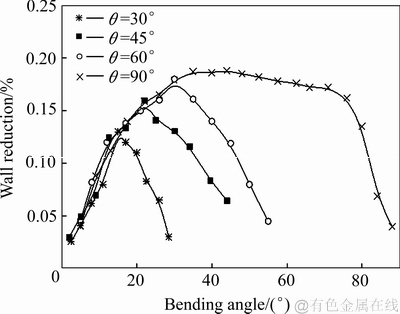
图6  对应管材角度位置的管外侧壁减薄量分布

Fig. 6  Relationship between bending angle and outer wall thickness reduction (ρ=40 mm)

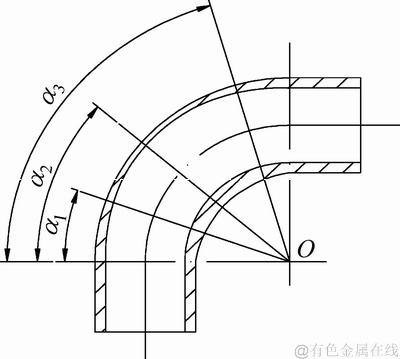
图7 角度位置含义示意图

Fig. 7  Illustration of angle position

这个角度位置是指管件弯曲弧线上点的法线方向与弯管开始变形点处的法线方向的夹角。角度位置如图7所示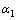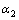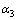，、、就是不同角度位置。它是用角度来标识的管材弯曲弧上不同点的法向断面的位置，是位置的概念。

图6中管件弯曲角度θ=30°的曲线，描述的是ρ=40 mm情况下，管件总弯曲角θ=30°时的外侧壁壁厚分布；管件弯曲角度θ=45°的曲线，描述的是ρ=40 mm情况下，管件总弯曲角θ=45°时的外侧壁壁厚分布；依次类推。由图6可见，管件总弯曲角度小于60°时，不能直接利用公式(1)来计算最小壁厚值。

对于小半径弯曲，管材壁厚减薄过渡区所占角度范围较大，工艺分析计算时要有所区别。对于本文研究的波导管(内腔15.8 mm×7.9 mm、壁厚1.0 mm)，ρ=40 mm，管件弯曲角度小于60°时，稳定变形区尚未出现，此时最大壁厚减薄量与弯曲角度有关；只有当管件弯曲角度θ大于60°时，外侧壁减薄变形出现稳定阶段，此时最大壁厚减薄量与弯曲角度无关，维持基本不变，可采用式(1)简化计算。

3.2  管材弯曲件的壁厚分布验证

图8所示为实验弯曲的波导管件剖切图，实验条件：弯曲曲率半径ρ=40 mm，顶推力采用170 N，芯棒支撑角度取30°。现将实测壁厚减薄率与数值模拟壁厚减薄率列于图9中进行对比，实测壁厚减薄率与模拟结果吻合较好，除去两端10°内急剧变化区域，最大减薄率误差小于2%，模拟结果具有较高的可信度。

图8  实验弯曲的波导管件剖切图

Fig. 8  Longitudinal cross section of sample bend

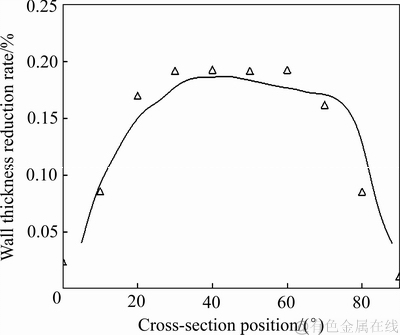
图9  实验值与模拟值对比曲线

Fig. 9  Comparison of empirically measured rates of wall thickness reduction vs modelled values (ρ=40 mm)

3.3  弯曲变形过渡区域壁厚的简化计算式

由图2和图6可知，管材弯曲达到稳定变形阶段后，已变形区部分的最小壁厚基本保持不变，而在已变形区前后两端的变形过渡区域内，壁厚值变化与其所在弯曲弧线上的角度位置变化近似成线性关系，这种线性关系的斜率与弯曲变形程度有关。

弯曲变形程度对于矩形波导管来讲，可以用ρ/(H+2T)来描述(实际上就是类似圆管弯曲时的ρ/d，d为圆管外径)；对矩形管参考图2，B=(H+2T)，则壁厚变化与弯曲角度的线性关系与ρ/B值相关。分析图2和图6可知，对于ρ=100 mm弯曲，过渡区弧长所对应的圆心角约13°；ρ=80 mm弯曲，过渡区弧长所对应的圆心角约16°；ρ=40 mm弯曲，过渡区弧长所对应的圆心角约为30°。将过渡区圆心角转化为弧度，可得：ρ=100 mm时，过渡区中性层弧长22.67 mm；ρ=80 mm时，过渡区中性层弧长22.33 mm；ρ=40 mm时，过渡区中性层弧长20.93 mm。

由此可见，尽管不同弯曲半径管件的变形过渡区范围不同，但是过渡区中性层弧长数值上极为接近，可见过渡区弧长与管材断面尺寸相关，与弯曲半径关系不大，针对本文研究的管材(内腔15.8 mm×7.9 mm，壁厚1.0 mm)过渡区弧长可以近似记为弯曲曲率所在平面内管材宽度B的1.2倍。

由图9模拟计算结果可以看出，变形过渡区内壁厚变化量与弯曲角度位置相关，壁厚急剧变化段接近于线性分布，仅当过渡区接近已变形区域才偏离线性分布。为简化计算，将图9的曲线简化成折线“Π”的形式，即假设过渡区壁厚呈线性分布，则可以得出过渡区域内壁厚的简化计算公式：

当时，有

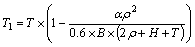              (3)

利用式(3)可算出过渡区域内管件的壁厚减小值，也可用于预测小角度弯曲时管材最大壁厚减薄量。

4  其他工艺参数对管壁减薄的影响

4.1  相对弯曲半径ρ/B的影响

相对弯曲半径ρ/B(ρ为弯曲中性层半径，B为弯曲曲率所在平面内管材的宽度)分别取2.23、2.81、3.37、4.49、5.62。相对弯曲半径ρ/B对最大壁厚减薄率影响的模拟统计结果如图10所示。

图10曲线变化趋势表明：随着相对弯曲半径ρ/B的增大，管壁的最大壁厚减薄率呈近似线性规律减小的趋势。ρ/B值实际上代表的是弯曲变形程度，其数值越小弯曲变形程度越大，壁厚减薄越严重，当ρ/B接近2时，壁厚减薄量约为20%。如果弯管产品有许可的最大壁厚减薄量的限制，就应该综合考虑施加轴向压力。

4.2  轴向压力(顶推力)的影响

弯曲半径ρ=40 mm，顶推力加在整个管坯后端面上，大小分别取为100、130、170、250 和300 N。

顶推力对最大壁厚减薄率影响的模拟统计结果如图11所示。

图10  相对弯曲半径ρ/B对最大壁厚减薄率的影响

Fig. 10  Influence of ρ/B on maximum rate of wall thickness reduction

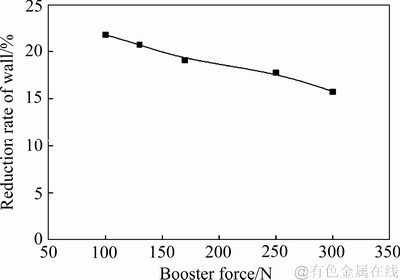
图11  顶推力对最大壁厚减薄量的影响曲线

Fig. 11  Effect of booster force on maximum rate of reduction of wall thickness

由图11可知：随着顶推力F的增大，管壁的最大壁厚减薄率逐渐减小。这是因为顶推力使应力中性层外移，从而减小了弯曲外侧受拉的变形程度，减小了壁厚减薄量。需要注意的是，增加顶推力实际上直接增加了弯曲管材内侧壁的轴向压力，加大了起皱风险，因此，施加轴向力通常以内侧壁不起皱为限。模具型腔参数以及芯棒参数可以一定程度上抑制起皱的发生。顶推力对壁厚减薄率的影响略偏离线性关系，这是因为弯曲内侧壁厚增加，减少了顶推力对外侧壁厚减薄的控制效果造成的。

4.3  芯棒支撑角度的影响

芯棒是影响矩形波导管弯曲成形质量的一个核心部件，其作用是在管坯内腔支撑管壁，防止横截面严重畸变和弯曲内侧壁起皱。芯棒支撑角度是个重要工艺参数，对弯管质量影响很大。支撑角度的定义就是指由芯棒所支撑的管材弯曲段的圆心角(见图12)。

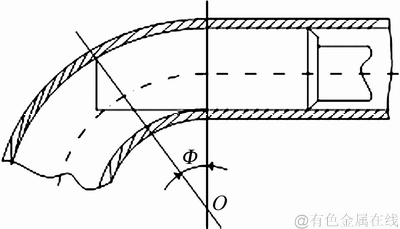
图12  芯棒支撑角示意图

Fig. 12  Illustration of mandrel support angle

计算时，弯曲半径ρ=40 mm，采用刚性舌式芯棒，支撑角度分别取Φ=20°、Φ=25°、Φ=30°、Φ=35°、Φ=40°。

芯棒支撑角度对最大壁厚减薄率影响的模拟统计结果如图13所示。

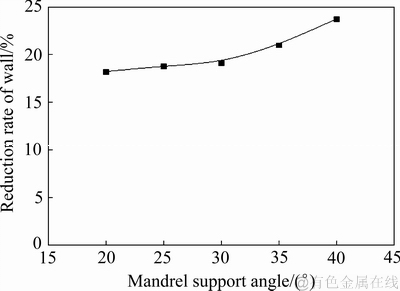
图13  芯棒支撑角度对最大壁厚减薄率的影响曲线

Fig. 13  Impact of mandrel support angles on max rate of reduction of wall thickness

从图13的曲线变化趋势可以看出，最大壁厚减薄率随着芯棒支撑角度的增大而增大。其原因集中在两个方面：1) 支撑角度大，则管材断面畸变小，外侧壁受拉成分加大，外侧壁延伸量加大，壁厚减薄量增加。2) 支撑角度大，则芯棒与管材接触面积大，摩擦力增大，材料流动阻力增加，管材弯曲外侧壁受拉成分加大，所以造成壁厚减薄量增加。由图13中可以看出，芯棒支撑角度在30°以下时对壁厚减薄影响较小，况且壁厚减薄过渡区刚好是30°范围，所以芯棒支撑角度应取30°为宜。

4.4  相对壁厚T/B的影响

相对壁厚T/B，是管材壁厚T与弯曲曲率所在平面内管材的宽度B的比值，是描述管材自身参数的物理量。壁厚T分别取1、1.25、1.5、2和2.5 mm；管材宽度B=17.8，弯曲半径ρ=40 mm。相对壁厚T/B对最大壁厚减薄率影响的模拟统计结果如图14所示。

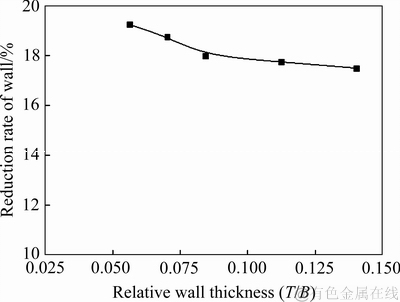
图14  相对壁厚T/B对最大壁厚减薄率的影响曲线

Fig. 14  Impact of relative wall thickness T/B on max rate of reduction of wall thickness

由图14可以看出：随着相对壁厚T/B的增大，管壁的最大壁厚减薄率呈减小的趋势，但这种减小变化不大。这是因为管材宽度B不变的情况下，管材壁厚越厚，对周边材料的牵扯变形能力越强，也就是说相对壁厚越大，管材壁厚减薄的分布相对更加分散，管材壁厚减薄量就会变小。

4.5  摩擦条件的影响

弯曲半径ρ=40 mm，管坯内腔与芯棒之间摩擦因数μ分别取为0.01、0.02、0.03、0.05、0.1。摩擦条件对最大壁厚减薄率影响的模拟统计结果如图15所示。

由图15可知：随着摩擦因数的增大，管壁的最大壁厚减薄率呈上升增加的趋势。原因是管壁与芯棒间较大的摩擦力增加了外侧壁材料的内部拉应力，且增加了材料流动阻力，使壁厚减薄增加。材料流动变得困难，管材弯曲时也很容易发生破裂。因此，芯棒表面要制作光滑并施加润滑剂，从而改善摩擦条件，提高管材弯曲成形极限。

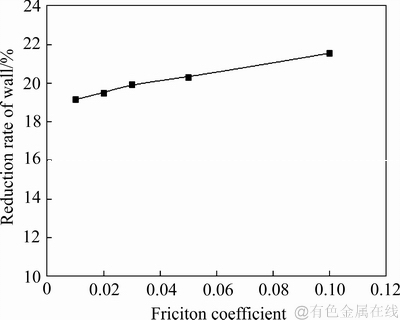
图15  摩擦因数对最大壁厚减薄率的影响曲线

Fig. 15  Relationship between friction coefficient and max rate of reduction of wall thickness

5  结论

1) 弯曲半径(相对弯曲半径ρ/B)是壁厚减薄的主要决定因素，简化计算时可适当忽略其他影响因素。小半径弯曲时为避免壁厚过度减薄，可以综合施加轴向压力和降低支撑芯棒与管壁摩擦因数。

2) 对于小半径弯曲，管材壁厚减薄过渡区所占角度范围较大，管件弯曲角度较小时，变形稳定区尚未出现，此时最大壁厚减薄量与弯曲角度有关；只有当管件弯曲角度大于某临界值，弯曲变形出现稳定阶段，此时最大壁厚减薄量与弯曲角度无关，维持基本不变。

3) 基于对内腔15.8 mm×7.9 mm、壁厚1.0 mm的波导管壁厚减薄过渡区域进行分析，得出了变形过渡区长度约为管材弯曲面内宽度B的1.2倍。同时提出了小半径弯曲矩形管考虑过渡区域的最小壁厚简化计算方法。

4) 芯棒支撑角度取壁厚过渡区宽度即可。小半径弯曲情况下芯棒支撑角度可取30°。

REFERENCES

[1] YANG He, LI Heng, ZHANG Zhi-yong, ZHAN Mei, LIU Jing, LI Guang-jun. Advances and trends on tube bending forming technologies[J]. Chinese Journal of Aeronautics, 2012, 25: 1-12.

[2] YUAN Si-bo, YU Zhen-tao, HAN Jian-ye, LIU Hui, HUANG Pu-qiang, MA Xi-qun. Technical research on small-radius bends of thin-walled capillary tube made from a new β-type titanium alloy[J]. Chinese Journal of Rare Metals, 2010, 34(5): 668-672.

[3] GOODARZI M, KUBOKI T, MURATA M. Effect of initial thickness on shear bending process of circular tubes[J]. Journal of Materials Processing Technology, 2007, 191(1/3): 136-140.

[4] TANG N C. Plastic-deformation analysis in tube bending[J]. International Journal of Pressure Vessels and Piping, 2000, 77(12): 751-759.

[5] STACHOWICZ F. Bending with upsetting of copper tube elbows[J]. Journal of Materials Processing Technology, 2000, 100(1/3): 236-240.

[6] LAZARESCU L. Effect of internal fluid pressure on quality of aluminum alloy tube in rotary draw bending[J]. International Journal of Advanced Manufacturing Technology, 2013, 64(1/4): 85-91.

[7] MILLER J E, KYRIAKIDES S, BASTARD A H. On bend-stretch forming aluminum extruded tubes—Ⅰ: Experiments[J]. International Journal of Mechanical Sciences, 2001, 43: 1283-1317.

[8] 尹承禹. 22MnB5矩形管弯曲成形极限研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.

YIN Cheng-yu. Research on bend forming limit for rectangular tube for 22MnB5[D]. Harbin: Harbin Institute of Technology, 2015.

[9] 岳永保, 杨 合, 詹 梅, 寇永乐, 李 恒. 薄壁管小弯曲半径数控弯曲壁厚减薄实验研究[J]. 锻压技术, 2007, 32(5): 58-62.

YUE Yong-bao, YANG He, ZHAN Mei, KOU Yong-le, LI Heng. Experimental study on thinning of thin-walled tube NC bending process with small bending radius[J]. Forging & Stamping Technology, 2007, 32(5): 58-62.

[10] 寇永乐, 杨 合, 詹 梅, 岳永保, 李 恒. 薄壁管数控弯曲截面畸变的实验研究[J]. 塑性工程学报, 2007, 14(5): 26-31.

KOU Yong-le, YANG He, ZHAN Mei, YUE Yong-bao, LI Heng. Experimental study on cross-section distortion of thin-walled tube in NC bending process[J]. Journal of Plasticity Engineering, 2007, 14(5): 26-31.

[11] YANG He, LI Heng, ZHAN Mei. Friction role in bending behaviors of thin-walled tube in rotary-draw-bending under small bending radius[J]. Journal of Materials Processing Technology, 2010, 210(15): 2273-2284.

[12] ZHAO Gang-yao, LIU Yu-li, YANG He, LU Cai-hong. Cross-sectional distortion behaviors of thin-walled rectangular tube in rotary-draw bending process[J]. Transactions of Nonferrous Metal Society of China, 2010, 20(3): 484-489.

[13] TIAN Shan, LIU Yu-li, YANG He. Effects of geometrical parameters on wrinkling of thin-walled rectangular aluminum alloy wave-guide tubes in rotary-draw bending[J]. Chinese Journal of Aeronautics, 2013, 26(1): 242-248.

[14] 袁文斌. 矩形波导管弯曲变形数值分析[D]. 北京: 北京科技大学，2006.

YUAN Wen-bin. The numerical value analysis of rectangular wave-guide tube bend deformation[D]. Beijing: University of Science and Technology Beijing, 2006.

[15] 胡福泰, 彭加耕, 臧新良, 汪飞雪. 矩形波导管弯曲壁厚减薄特点分析[J]. 塑性工程学报, 2018, 25(5): 212-216.

HU Fu-tai, PENG Jia-geng, ZANG Xin-liang, WANG Fei-xue. Practical analysis of wall thickness in rectangular waveguide bends[J]. Journal of Plasticity Engineering, 2018, 25(5): 212-216.

Influence of bending parameters of waveguide on wall thickness reduction

HU Fu-tai, WANG Fei-xue, ZANG Xin-liang, PENG Jia-geng

(School of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China)

Abstract: This investigation established a finite element analysis model to determine the distribution of wall thickness in taper zones of 6063 waveguide bends with various radii, and demonstrated the relationship between wall thicknesses in the stable deformation zones and the bending radii. For the given waveguide with the chamber size of 15.8 mm in width, 7.9 mm in height and 1.0 mm in wall thickness, the distribution of outer wall thickness was calculated for a range of angles of bend at ρ=40 mm, and it was observed that the taper zone can extend to an angular range of 30° and greater. The calculated and empirical measured wall thickness values of 90° bends were compared, and apart from the 10° of abrupt tapering at either ends of the bend, the calculated rates of thickness reduction had errors of less than 2%. In addition, the arc-lengths of the neutral axes of the taper zones were also determined to be approximately 1.2 times the width B of the tube, and a formula to calculate wall thickness with angular correction was derived. Calculations also revealed that the mandrel support regions should coincide with the range of the taper zones, and that in the bends with small radii, the angular ranges could reach 30° or more. This report also analyzed other factors and their theoretical contributions to wall thickness variation, including the force exerted by the booster on the tube, coefficient of friction and mandrel support angle. These analytical calculations can provide a theoretical basis for the improvement of waveguide bends manufacturing process and research.

Key words: waveguide bending; bending process; wall thickness reduction; taper zone

Foundation item: Project(E2017203127) supported by the Natural Science Foundation of Hebei Province, China; Project(8190004) supported by the Foundation for Doctoral Scientists of Yanshan University, China

Received date: 2018-08-12; Accepted date: 2019-04-10

Corresponding author: HU Fu-tai; Tel: +86-13933958170; E-mail: hufutai@sina.com

(编辑  何学锋)

基金项目：河北省自然科学基金资助项目(E2017203127)；燕山大学博士基金资助项目(8190004)

收稿日期：2018-08-12；修订日期：2019-04-10

通信作者：胡福泰，副教授，博士，电话：13933958170；E-mail：hufutai@sina.com