J. Cent. South Univ. (2012) 19: 1999-2007
DOI: 10.1007/s11771-012-1237-5
Longitudinal dynamic response of pile in layered soil based on virtual soil pile model
WU Wen-bing(吴文兵)1,2, WANG Kui-hua(王奎华)1, MA Shao-jun(马少俊)1, CHIN Jian Leo3
1. Key Laboratory of Soft Soils and Geoenvironmental Engineering of Ministry of Education
(Zhejiang University), Hangzhou 310058, China;
2. Engineering Faulty, China University of Geosciences, Wuhan 430074, China;
3. School of Engineering, University of Western Sydney, Sydney, NSW 1797, Australia
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: Taking the effect of finite soil layers below pile end into account, the longitudinal dynamic response of pile undergoing dynamic loading in layered soil was theoretically investigated. Firstly, finite soil layers below pile end are modeled as virtual soil pile whose cross-section area is the same as that of the pile and the soil layers surrounding the pile are described by the plane strain model. Then, by virtue of Laplace transform and impedance function transfer method, the analytical solution of longitudinal dynamic response at the pile head in frequency domain is yielded. Also, the semi-analytical solution in time domain undergoing half-cycle sine pulse at the pile head is obtained by means of inverse Laplace transform. Based on these solutions, a parametric study is conducted to analyze emphatically the effects of parameters of soil below pile end on velocity admittance and reflected wave signals at the pile head. Additionally, a comparison with other models with different supporting conditions from soil below pile end is performed to verify the model presented.
Key words: soil-pile dynamic interaction; virtual soil pile; layered soil; longitudinal vibration; velocity admittance; reflected wave signal
1 Introduction
Over the past decades, many soil-pile dynamic interaction models have been developed to investigate the behavior of longitudinal vibration of pile. From the view point of surrounding soil-pile dynamic interaction, these models can be divided into three categories, that is, dynamic Winkler model [1-11], plane-strain model [12-22] and three-dimensional axisymmetric continuum model [23-28]. It can be noted that extensive and in-depth research work has been done in the field of surrounding soil-pile dynamic interaction. By contrast, less attention is attracted by the topic on underlying soil-pile dynamic interaction. However, the support condition of pile end soil has significant influence on the dynamic response of soil-pile system. For instance, the support stiffness of pile end soil is the leading factor on the longitudinal resonance frequency at the pile head. The resonance frequency at the pile head is a significant parameter in earthquake-resistance design, for the superstructure may be destroyed when resonance frequency at the pile head is equal or close to the natural frequency of vibration of the superstructure. The support stiffness of pile end soil also affects the characteristic and shape of reflected wave curve of the pile toe, which plays an important role in pile integrity testing and quantitative defect inversion analysis. Furthermore, the damping of the pile end soil can also greatly affect velocity admittance curve and reflected wave curve.
In the existing literatures, there are two basic approaches to simulate the support condition of pile end soil. In the first approach, it is assumed to be rigid model [2-3, 12, 23, 28]. Such a simplified model is not sufficiently accurate unless the pile is end bearing. In the second approach, it is assumed to be elastic model (modeled by a linear spring) [10, 26-27] or viscoelastic model (modeled by a linear spring and a dashpot connected in parallel) [1, 5-6, 8-9, 11]. Although these methods are amenable to practical application in pile nondestructive testing, the parameters of spring and dashpot cannot be obtained by associating with those of the pile end soil. Although great progress has been made in surrounding soil-pile dynamic interaction, it is far from enough when it comes to the interaction between pile and pile end soil. But such a topic is very important in order to gain a profound insight into soil-pile dynamic interaction and thus worth an in-depth investigation. In light of this, the objective of this work is to derive an extended soil-pile dynamic interaction model to simulate the effects of pile end soil parameters on the dynamic response of the pile.
2 Governing equations
2.1 Schematic of soil-pile model
The problem investigated herein is the longitudinal vibration behavior of a pile embedded in layered soil. The schematic diagram of soil-pile model is shown in Fig. 1, where the pile end soil is modeled as virtual soil pile. As shown in Fig. 1, the basic idea of virtual soil pile model is that the finite soil layers underlying the pile toe are assumed to be soil column, viz virtual soil pile whose cross-section area is the same as the pile. The virtual soil pile satisfies the plane section deformation assumption. Allowing for the variation of modulus or cross-sectional dimension of the pile or soil properties, the soil-pile (including virtual soil pile) system is discretized into a total of m segments numbered by 1, 2, …, j, …, m from virtual soil pile toe to pile head. The thickness of the j-th (1≤j≤m) soil layer is denoted by lj and the depth of the j-th (1≤j≤m) soil layer top is denoted by hj. The properties of pile (including virtual soil pile) and surrounding soil layer are assumed to be homogeneous within each segment, but may vary from segment to segment. In the j-th pile (including virtual soil pile) segment (1≤j≤m), the density and radius of the pile are denoted by ρpj and rj, respectively.
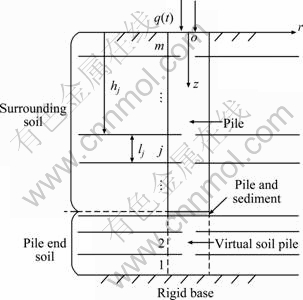
Fig. 1 Schematic diagram of soil-pile interaction model
The main assumptions adopted in this work are as follows:
1) The excitation is harmonic longitudinally. The soil-pile system is subjected to small deformations and strains during vibration. The pile is perfectly elastic with circular cross section.
2) The dynamic stress of soil transfers to the pile shaft through the complex stiffness on the contact surface of the every segment of surrounding soil-pile system or surrounding soil-virtual soil pile system.
3) The conditions of displacement continuity and force equilibrium are satisfied at the interface of virtual soil pile and pile end.
2.2 Equation of motion
2.2.1 Dynamic equation of soil
The plane strain model of soil vibration proposed by NOVAK [14] is adopted here. The dynamic equation of soil can be expressed as
 (1)
(1)
where  , is the longitudinal displacement of the j-th soil layer;
, is the longitudinal displacement of the j-th soil layer;  ,
,  ,
,
is the shear wave velocity of the j-th soil layer; ρj, Gj and Ds,j are density, shear modulus and material damping of the j-th soil layer, respectively; ω is circular frequency and  .
.
2.2.2 Dynamic equation of pile (including virtual soil pile)
The dynamic equation of pile can be derived as
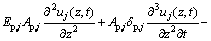
 (2)
(2)
where uj(z, t) is the longitudinal displacement of the j-th pile (including virtual soil pile) segment; Ep,j, mp,j, δp,j and  denote the elastic modulus, mass per unit length, viscous damping coefficient and cross-section area, respectively; fj(z, t)=KKjuj(z, t), is the frictional force that the j-th soil layer acts on the surface of the pile shaft; KKj is the longitudinal shear complex stiffness around the pile shaft in the j-th soil layer which can be derived by solving the dynamic equation of soil.
denote the elastic modulus, mass per unit length, viscous damping coefficient and cross-section area, respectively; fj(z, t)=KKjuj(z, t), is the frictional force that the j-th soil layer acts on the surface of the pile shaft; KKj is the longitudinal shear complex stiffness around the pile shaft in the j-th soil layer which can be derived by solving the dynamic equation of soil.
2.2.3 Conditions of soil-pile system
1) Boundary conditions (BCs) of pile and virtual soil pile
At the top of the pile:
 (3)
(3)
At the bottom of the virtual soil pile:
 (4)
(4)
where q(t) is the harmonic excitation acting on the pile head.
At the interface of the pile or virtual soil pile segments:
 (5)
(5)
2) Initial conditions (ICs) of pile and virtual soil pile
 (6)
(6)
3 Solution of equations
3.1 Vibrations of soil layer
Solving Eq. (1) for Wj(r) yields
 (7)
(7)
where I0(βjr) and K0(βjr) are the modified Bessel functions of order zero of the first and second kinds, respectively. Aj and Bj are constants determined by BCs. Utilizing BCs that stresses and displacements approach zero at an infinite radial distance, it can be obtained that Bj=0 from Eq. (7).
The longitudinal shear stress at any point in the soil layer can be expressed as
 (8)
(8)
where  .
.
Then, the longitudinal shear complex stiffness around the pile shaft of the j-th soil layer can be derived as
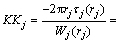
 (9)
(9)
where K1(βjrj) is the modified Bessel functions of order one of the second kind.
3.2 Longitudinal vibrations of pile and virtual soil pile
Let  be the Laplace transform of uj(z, t) with respect to t. Taking the Laplace transform of Eq. (2) and combining with the initial conditions Eq.(6) yields
be the Laplace transform of uj(z, t) with respect to t. Taking the Laplace transform of Eq. (2) and combining with the initial conditions Eq.(6) yields
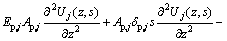
 (10)
(10)
Equation (10) can be further reduced as
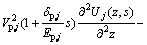
 (11)
(11)
where Vp,j, ρp,j and Ep,j are elastic longitudinal wave velocity, density and elastic modulus of the j-th pile (including virtual soil pile) segment, respectively, and  .
.
The general solution of Eq. (11) can be derived as
 (12)
(12)
where  is dimensionless
is dimensionless
eigenvalue; Cj and Dj are complex constants which can be obtained from BCs; tj=lj/Vp,j, denotes the propagation time of elastic longitudinal wave in the j-th pile (virtual soil pile) segment.
Combining with Eq. (4), the displacement impedance function at the top of the first virtual soil pile segment (z=h1) can be derived as
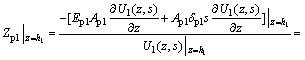
 (13)
(13)
where  , and Zp0 is the displacement function at the bottom of the virtual soil pile.
, and Zp0 is the displacement function at the bottom of the virtual soil pile.
Then, using the method of recursion that typically used in the transfer function technique, the displacement impedance function of the top of the j-th pile segment or virtual soil pile segment can be obtained as
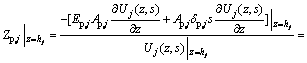
 (14)
(14)
where  .
.
Through further recursion, the displacement impedance function at the pile head can be obtained as
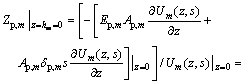
 (15)
(15)
where  is the dimensionless displacement impedance function at the pile head with
is the dimensionless displacement impedance function at the pile head with  .
.
The displacement impedance function can be further expressed in terms of its real part and imaginary part which represent the dynamic stiffness and damping, respectively. And the dynamic damping reflects the energy dissipation:
 (16)
(16)
The velocity transit function at the pile head can be written as
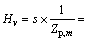
 (17)
(17)
Letting s=iω and substituting it into Eq. (17) yields the frequency response function of the velocity at the pile head:
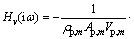
 (18)
(18)
Nondimensionalizing expression Eq. (18) yields the dimensionless velocity admittance of the pile head:
 (19)
(19)
where  and
and  denote the dimensionless frequency and dimensionless propagation time of elastic longitudinal wave in the m-th pile segment, respectively.
denote the dimensionless frequency and dimensionless propagation time of elastic longitudinal wave in the m-th pile segment, respectively.
By means of the inverse Fourier transform, the velocity response in the time domain at the pile head is obtained as V(t)=IFT[Q(ω)Hv(iω)], where Q(ω) denotes the Fourier transform of q(t), which is the longitudinal excitation acting on the pile head.
In particular, the excitation is a half-sine pulse as follows:
 (20)
(20)
where T0 and Qmax denote the duration of the impulse or impulse width and the maximum amplitude of the excitation, respectively. Then, the velocity response of the pile head can be expressed as
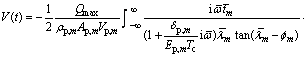
 (21)
(21)
The dimensionless velocity response can be derived as
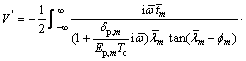
 (22)
(22)
where  ,
,  , t,
, t, 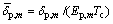
denote dimensionless pulse width, dimensionless time variable, usual time variable and dimensionless viscous damping coefficient, respectively; Tc denotes the propagation time of elastic longitudinal wave propagating from the pile head to the pile toe.
4 Parametric study and discussion
A parametric study is conducted to demonstrate the dynamic response properties of soil-pile system based on the solutions in Eq. (19) and Eq. (22).
4.1 Case of one pile end soil layer
In this case, the soil-pile system is discretized into two layers, namely, pile and pile end soil. The bottom of the pile end soil is base rock which can be assumed to be rigid. Parameters used here are as follows: length, mass density and elastic longitudinal wave velocity of the pile are 15 m, 2 500 kg/m3 and 4 000 m/s, respectively; mass density and shear wave velocity of the surrounding soil of the pile are 2 000 kg/m3 and 150 m/s, respectively; mass density and shear wave velocity of the pile end soil are 2 000 kg/m3 and 150 m/s, respectively; elastic longitudinal wave velocity and thickness of the pile end soil are Vp1=900 m/s and l1=1, 3, 5, 10 and 20 m, respectively, when analyzing the influence of the thickness of pile end soil on the pile dynamic response; elastic longitudinal wave velocity and thickness of the pile end soil are Vp1=1 000, 800, 600, 500, 300 m/s and l1=2 m, respectively, when analyzing the influence of the elastic longitudinal wave velocity of pile end soil on the pile dynamic response.
4.1.1 Influence of thickness of pile end soil on pile dynamic response
The influence of thickness of pile end soil on the velocity admittance is shown in Fig. 2. It can be seen that the velocity admittance curve gradually tends to be convergent as the thickness of pile end soil increases. As the thickness of pile end soil is beyond a threshold, say, 5 m in this case, further increase of thickness rarely gives rise to further change in the velocity admittance curve, which means that there is a critical influence depth of pile end soil. When the thickness is beyond this critical influence depth, further increase of the thickness of the pile end soil has little influence on the dynamic response of pile. Nevertheless, when the thickness of the pile end soil is less than this critical influence depth, it has significant influence on the velocity admittance.
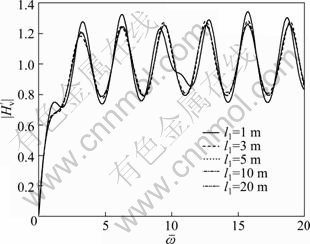
Fig. 2 Influence of thickness of pile end soil on velocity admittance
Figure 3 shows the influence of thickness of pile end soil on reflected wave signals. It is evident that the reflected wave curve also tends to be convergent as the thickness of pile end soil increases. The pile head will receive the reverse reflected signal back from the bedrock when the pile end soil is thin enough. The result also shows that there is a limited zone of pile end soil adjoining to the pile toe that has influence upon the reflected wave curve.
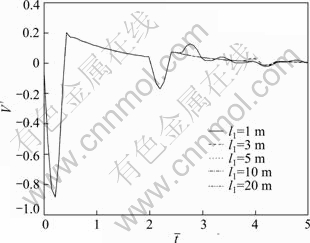
Fig. 3 Influence of thickness of pile end soil on reflected wave signals
4.1.2 Influence of elastic longitudinal wave velocity of pile end soil on pile dynamic response
The influence of elastic longitudinal wave velocity of pile end soil on the velocity admittance is shown in Fig. 4. It can be noted that the velocity admittance curve oscillates about mean amplitude as the frequency increases, and the amplitude of oscillation increases as the elastic longitudinal wave velocity of pile end soil decreases. The velocity admittance curve tends to be stable when the longitudinal wave velocity is small enough. The result shows that strengthening of soil decreases the amplitude of oscillation of the velocity admittance curve but intensifies the degree of oscillation.
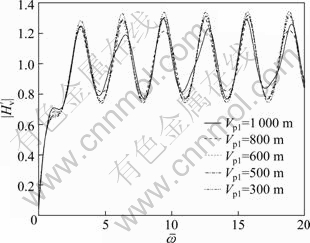
Fig. 4 Influence of elastic longitudinal wave velocity of pile end soil on velocity admittance
Figure 5 shows the influence of elastic longitudinal wave velocity of pile end soil on reflected wave signals. It is obvious that there are orthokinetic reflected signal at the interface of pile toe and the virtual soil pile head and reverse reflected signal at the surface of base rock. With the pile end soil weakening, the amplitude of the orthokinetic reflected signal of the pile toe increases but the width of signal is unchanged. The propagation time of reverse reflected signal increases and the superimposition of the reverse reflected signal and the second orthokinetic reflected at the virtual soil pile head leads the reverse reflected signal to weaken gradually until it disappears eventually.
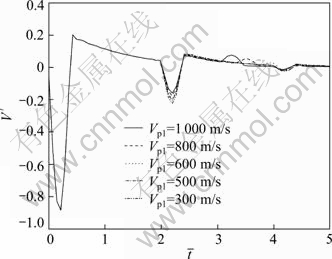
Fig. 5 Influence of elastic longitudinal wave velocity of pile end soil on reflected wave signals
4.2 Case of two pile end soil layers
In this case, the pile end soil is discretized into two layers. The upper layer is bearing stratum and the lower layer is soft subsoil. The bottom of the soft subsoil is base rock assumed to be rigid. Parameters used here are as follows. The parameters of pile and surrounding soil of the pile are the same values as those in Section 4.1; thickness, mass density, shear wave velocity and elastic longitudinal wave velocity of the bearing stratum are 3 m, 2 000 kg/m3, 150 m/s and 900 m/s, respectively; mass density and shear wave velocity of the soft subsoil are 1 800 kg/m3 and 80 m/s, respectively; elastic longitudinal wave velocity and thickness of the soft subsoil are Vp2=500 m/s and l2=0, 1, 3, 5, 10 m, respectively, when analyzing the influence of the thickness of soft subsoil on the pile dynamic response; elastic longitudinal wave velocity and thickness of soft subsoil are Vp2=600, 500, 400, 300, 200 m/s and l2=5 m, respectively, when analyzing the influence of the elastic longitudinal wave velocity of soft subsoil on the pile dynamic response.
4.2.1 Influence of thickness of soft subsoil on pile dynamic response
The influence of thickness of soft subsoil on the velocity admittance is shown in Fig. 6. It can be seen that the amplitude of resonance peaks decreases as the thickness of soft subsoil increases. But, as the thickness increases further, the thickness of soft subsoil has little effect on the velocity admittance curve.
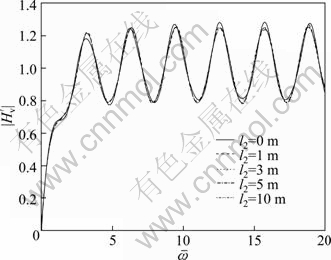
Fig. 6 Influence of thickness of soft subsoil on velocity admittance
Figure 7 shows the influence of thickness of soft subsoil on reflected wave signals. It is noted that the first reflected signal is barely affected by the thickness of soft subsoil. However, the amplitude of the second reflected signal decreases as the thickness of soft subsoil increases. This is due to rapid energy dissipation of stress wave with the thickness of soft subsoil increasing.
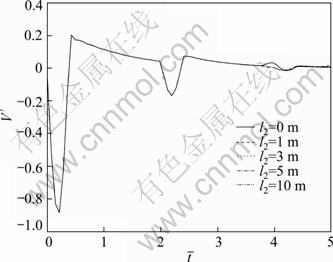
Fig. 7 Influence of thickness of soft subsoil on reflected wave signals
4.2.2 Influence of elastic longitudinal wave velocity of soft subsoil on pile dynamic response
Figures 8 and 9 show the influence of elastic longitudinal wave velocity of soft subsoil on the velocity admittance curve and reflected wave curve, respectively. It can be seen that the influence of elastic longitudinal wave velocity of soft subsoil on pile dynamic response can be neglected when the depth of bearing stratum is beyond a certain value, say, 3 m in this case. The results show that the properties of soft subsoil have little effect on the pile dynamic response when the bearing stratum is deep enough.
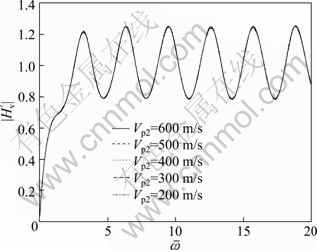
Fig. 8 Influence of elastic longitudinal wave velocity of soft subsoil on velocity admittance
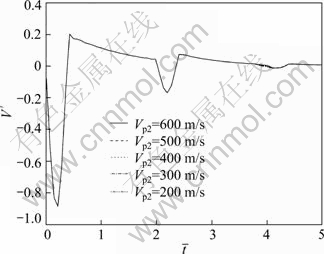
Fig. 9 Influence of elastic longitudinal wave velocity of soft subsoil on reflected wave signals
5 Comparison with other models
The virtual soil pile mode proposed here is compared with other models. The parameters of pile and surrounding soil of the pile are the same values as those in Section 4.1. Mass density, shear wave velocity, elastic longitudinal wave velocity and thickness of the pile end soil are 2 000 kg/m3, 150 m/s, 900 m/s and 2 m, respectively. Difference of models depends on the values of kb and ηb. The support condition of the pile can be regarded to be free if kb=0, ηb=0 and rigid if kb=∞, ηb=∞ and viscoelastic otherwise.
Figure 10 presents the comparison of velocity admittance at the top of pile with other models. It can be seen that the case of free support is out of phase relative to the case of rigid support (that is, the difference of phase angle is close to 180° ). The phase angle difference varies from 0° to 180° when the values of kb and ηb are other constants. It can also be seen that the amplitude of resonance peaks gradually decrease firstly and then gradually increase when the values of kb and ηb vary from zero to infinity.
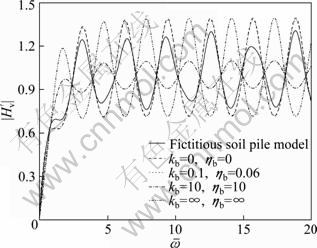
Fig. 10 Comparison of velocity admittance with other support models
Figure 11 shows the comparison of reflected wave signals with other models. It can be seen that the amplitude of reflected signal at the pile toe gradually decreases firstly and then increases when the values of kb and ηb vary from zero to infinity. The reflected signal is orthokinetic when the complex support stiffness is small (for example, kb=0, ηb=0 and kb=0.1, ηb=0.06). Meanwhile, the reflected signal is reverse when the complex supporting stiffness is large (for example, kb=10, ηb=10 and kb=∞, ηb=∞). The amplitude of reflected signal for the case of virtual soil pile model falls between that of free support and rigid support. The result means that the virtual soil pile model is reliable and can be simulated in other support models by varying parameters of pile end soil.
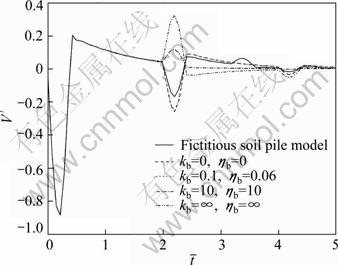
Fig. 11 Comparison of reflected wave signals with other support models
Although the viscoelastic support model is amenable to practical application, the values of kb and ηb are obtained depending on experience or other approximate methods. The results of comparison with virtual soil pile model to other support models show that the complex stiffness of the virtual soil pile falls between that of free support model and rigid support model. The virtual soil pile model approaches to free support model or rigid support model as the complex stiffness at the top of virtual soil pile is teeny or maximal. Therefore, virtual soil pile model has an advantage that its parameters can be associated to the properties of the pile end soil directly. Taking such an advantage and combining with parametric fitting method, we can obtain the relationship between the properties of pile end soil and its corresponding complex support stiffness. Such relationship can provide reliable calculating parameters for earthquake-resistance design and various methods of dynamic testing of pile.
6 Conclusions
1) A virtual soil pile model is proposed. Taking the effect of finite pile end soil into account, the longitudinal vibration of a pile embedded in layered soil is investigated. The analytical solution in the frequency domain and the corresponding semi-analytical solutions in time domain for the dynamic response of the pile undergoing longitudinal harmonic excitation are derived. The parameter study shows that the vibration characteristics of the soil-pile system are affected not only by the interaction between the pile and the surrounding soil layer but also by the interaction between the pile and the pile end soil.
2) The finite pile end soil layer adjacent to the pile toe has a significant influence on the pile dynamic response. There is a critical influence depth for pile end soil. When the thickness is within the critical influence, the increase of the thickness of the pile end soil can dramatically affect the dynamic response of the pile. Nevertheless, when the thickness of the pile end soil is beyond the critical influence depth, the further increase of the thickness of the pile end soil has little influence on the dynamic response of pile.
3) For the velocity admittance curves, the amplitude of oscillation increases as the elastic longitudinal wave velocity of pile end soil decreases. The soil weakening increases the amplitude of oscillation but weakens the oscillating degree. For reflected wave curves, the amplitude of orthokinetic reflected signal of the pile toe increases with the pile end soil weakening.
4) Comparison with other support models shows that the complex stiffness of the virtual soil pile head falls between that of free support model and rigid support model. This means that the virtual soil pile model is reliable and can be simulated by varying parameters of pile end soil.
References
[1] NOVAK M, BEREDUGO Y O. Longitudinal vibration of embedded footings [J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1972, 98: 1291-1310.
[2] NOGAMIT T, KONAGAI K. Dynamic response of longitudinally loaded nonlinear pile foundations [J]. Journal of Geotechnical Engineering Division, ASCE, 1987, 113: 147-160.
[3] NOGAMIT T, KONAGAI K. Time domain flexural response of dynamically loaded single piles [J]. Journal Engineering Mechanics Division, ASCE, 1988, 114: 1512-1525.
[4] NAGGAR M H E I, NOVAK M. Nonlinear analysis for dynamic lateral pile response [J]. Soil Dynamics and Earthquake Engineering, 1996, 15: 233-244.
[5] LIAO S T, ROESSET J M, Dynamic response of intact piles to impulse loads [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1997, 22: 255-275.
[6] LIAO S T, ROESSET J M. Identification of defects in piles through dynamic testing [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1997, 21: 277-291.
[7] MICHAELIDES O, GAZETAS G, BOUCKOVALAS G, CHPYSIKOU E, Approximate non-linear dynamic axial response of piles [J]. Geotechnique, 1998, 48: 33-53.
[8] RANDOLPH M F, SIMONS H A. An improved soil model for one-dimensional pile driving analysis. Proc [C]// 3rd Int Conf on Numerical Methods in Offshore Piling. Nantes, 1986: 3-17.
[9] RANDOLPH M F, DEEKS A J. Dynamic and static soil models for axial response [C]// Proc 4th Int Conf on the Application of Stress Wave Theory to Piles. The Hague, 1992: 3-14.
[10] WANG Kui-hua. A study on longitudinal vibration of pile with inhomogeneous cross section acoustic impedance with Laplace Transform [J]. Acta Mechnica Sinica, 2001, 33: 479-491. (in Chinese)
[11] WANG K H, WU W B, ZHANG Z Q, LEO C J. Longitudinal dynamic response of an inhomogeneous viscoelastic pile [J]. Computers and Geotechnics, 2010, 37: 536-544.
[12] NOVAK M. Dynamic stiffness and damping of piles [J]. Canadian Geotechnical Journal, 1974, 11: 574-598.
[13] NOVAK M. Longitudinal vibration of floating pile [J]. Journal of the Engineering Mechanical Division, ASCE, 1977, 103: 153-168.
[14] NOVAK M, NOGAMI T, ABOUL-ELLA F. Dynamic soil reactions for plane strain case [J]. Journal of the Engineering Mechanical Division, ASCE, 1978, 104: 953-959.
[15] RAJAPAKSE R K N D, SHAH A H. On the longitudinal harmonic motion of an elastic bar embedded in an elastic half-space [J]. International Journal of Solids and Structures, 1978, 23: 267-285.
[16] RAJAPAKSE R K N D, SHAH A H. Impedance curves for an elastic pile [J]. International Journal of Soil Dynamics and Earthquake Engineering, 1989, 8: 145-152.
[17] MAMOON S M, BANERJEE P K. Time-domain analysis of dynamically loaded single piles [J]. Journal of the Engineering Mechanical Division, ASCE, 1992, 118: 140-146.
[18] HAN Y C. Coupled vibration of embedded foundation [J]. Journal of Geotechnical Engineering Division, ASCE, 1989, 115: 1227-1238.
[19] HAN Y C. Dynamic longitudinal response of piles in nonlinear soil [J]. Journal of Geotechnical and Geoenvironmental Engineering Division, ASCE, 1997, 123: 710-716.
[20] MILITANO G, RAJAPAKSE R K N D. Dynamic response of a pile in a multi-layered soil to transient torsional and axial loading [J]. Geotechnique, 1999, 49: 91-109.
[21] NAGGAR M H E I, NOVAK M. Nonlinear axial interaction in pile dynamics [J]. Journal of Geotechnical Engineering Division, ASCE, 1994, 120: 678-695.
[22] NAGGAR M H E I, NOVAK M. Nonlinear lateral interaction in pile dynamics [J]. Soil Dynamics and Earthquake Engineering, 1995, 14: 141-157.
[23] NOGAMI T, NOVAK M. Soil-pile interaction in longitudinal vibration [J]. Earthquake Engineering and Structural Dynamics, 1976, 4: 277-293.
[24] ZENG X, RAJAPAKSE R K N D. Dynamic axial load transfer from elastic bar to poroelastic medium [J]. Journal of the Engineering Mechanical Division, ASCE, 1999, 125: 1048-1055.
[25] HESHAM M, NAGGAR M H E I. Longitudinal and torsional soil reactions for radially inhomogeneous soil layer [J]. Structural Engineering and Mechanics, 2000, 10: 299-312.
[26] HU Chang-bin, WANG Kui-hua, XIE Kang-he. Soil-pile interaction in longitudinal vibrations of a pile with elastic bottom boundaries and its application [J]. Engineering Mechanics, 2003, 20: 146-154. (in Chinese)
[27] YANG D Y, WANG K H, ZHANG Z Q, LEO C J. Longitudinal dynamic response of pile in a radially heterogeneous soil layer [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 33: 1039-1054.
[28] WANG K H, ZHANG Z Q, XIE K H, LEO C J. Dynamic torsional response of an end bearing in transversely isotropic saturated soil [J]. Journal of Sound and Vibration, 2009, 327: 440-453.
(Edited by YANG Bing)
Foundation item: Project(50879077) supported by the National Natural Science Foundation of China
Received date: 2011-04-27; Accepted date: 2011-07-12
Corresponding author: WANG Kui-hua, PhD; Tel: +86-571-88208708; E-mail: zdwkh0618@zju.edu.cn