
求解并联冷机负荷分配问题的改进FODPSO算法
于军琪,赵泽华,赵安军,王福,陈时羽
(西安建筑科技大学 建筑设备科学与工程学院,陕西 西安,710055)
摘要:针对并联冷机负荷分配问题,以系统总功率最小为优化目标,建立满足系统末端负荷需求的并联冷机负荷分配优化模型,提出一种改进分数阶达尔文粒子群优化(IFODPSO)算法,以每台冷机的部分负荷率为优化变量进行求解,优化并联冷机系统的运行策略以节能。首先,针对基本分数阶达尔文粒子群优化(FODPSO)算法粒子初始化过于分散的问题,提出利用蒙特卡洛方法结合基本算数运算符生成初始种群;其次,针对其在高维优化中难以同时搜寻到每一维最优解的问题,引入多重优化提高算法稳定性并加快收敛速度;第三,针对易陷入局部最优的问题,通过自适应多策略行为使粒子能够根据其适应度选择合适的更新方式,提高了算法的搜索能力;最后,以2个典型的并联冷机系统作为案例验证所提出算法的性能,并与其他现有优化算法的实验结果进行对比。研究结果表明:相比于其他算法,IFODPSO算法在并联冷机负荷分配问题的求解中能够取得更加显著的节能效果,得到更优的运行策略,同时收敛精度、收敛速度和稳定性都有了显著提高。
关键词:负荷分配;并联冷机;分数阶达尔文粒子群优化算法;蒙特卡洛;多重优化;自适应多策略
中图分类号:TU831.6 文献标志码:A 开放科学(资源服务)标识码(OSID)
文章编号:1672-7207(2021)06-1901-14
Improved FODPSO algorithm for load distribution of parallel chillers
YU Junqi, ZHAO Zehua, ZHAO Anjun, WANG Fu, CHEN Shiyu
(School of Building Equipment Science and Engineering, Xi'an University of Architecture and Technology, Xi'an 710055, China)
Abstract: Aiming at load distribution problem of parallel chillers, an optimization model of load distribution of parallel chillers was established and the end load requirement was satisfied. An improved fractional order Darwinian particle swarm optimization(IFODPSO) algorithm was proposed to optimize the operation strategy with the partial load rate of each chiller as the optimization variable to save energy. Firstly, Monte Carlo method combined with the basic arithmetic operator was used to solve the problem of too much scattered particle initialization in the basic fractional order Darwinian particle swarm optimization(FODPSO) algorithm. Secondly, multi-optimization was introduced to find the optimal solution of each dimension at the same time, which improved the stability and accelerated the convergence speed of the algorithm. Thirdly, the adaptive multi-strategy behavior enabled particles to choose appropriate update mode according to its fitness to improve the search ability of the algorithm for local optimal problem. Finally, two typical parallel chiller systems were taken as examples to verify the performance of the proposed algorithm, and the experimental results of other existing optimization algorithms were compared. The results show that compared with other algorithms, IFODPSO algorithm can achieve more significant energy-saving effect in solving the load distribution problem of parallel chillers, and can search for a better operation strategy. Meanwhile, the convergence accuracy, convergence speed and stability are significantly improved.
Key words: load distribution; parallel chiller system; fractional order Darwinian particle swarm optimization algorithm(FODPSO); Monte Carlo; multi-optimization; adaptive multi-strategy
近年来,随着人们对舒适性要求的不断提高,作为中央空调系统的主要耗能设备的冷水机组在大型公共建筑中得到了更加广泛的应用,其运行能耗约占中央空调系统总能耗的60%,而该能耗约占建筑总能耗的25%~40%[1]。由于不同类型的冷机具有不同额定容量和性能参数,可以通过调控各冷机的运行工况满足不同的末端负荷需求,从而大幅提高系统的灵活性[2]。因此,如何提高并联冷机系统的运行效率使其运行能耗最低成为当代建筑节能的研究课题之一。
研究人员采取许多优化算法解决并联冷机负荷分配(optimal chiller loading,OCL)问题。CHANG[3]采用拉格朗日法(Lagrange method,LM)求解OCL问题,发现虽然该法较传统的平均负荷法能耗更低,但在较低负荷需求下无法收敛;CHANG等[4]又提出梯度法(gradient method,GM)解决该问题,GM克服了LM收敛性差的缺点,但其迭代步骤偏多且求解精度略低。近年来,许多元启发式算法也被用于解决OCL问题。CHANG[5]采用遗传算法(genetic algorithm,GA)克服了LM在面对非凸函数时不适用的缺点,但无法有效降低能耗;LEE等[6]采用粒子群算法(particle swarm optimization,PSO)求解该问题,发现PSO算法在该问题上的寻优效果优于GA算法;CHANG等[7]又提出模拟退火算法(simulated annealing,SA),发现该方法能快速产生精度较高的结果;LEE等[2]针对该问题采用差分进化算法(differential evolution,DE)求解,取得了和PSO算法一致的优化结果,但其平均能耗更低;COELHO等[8-9]提出基于高斯分布函数改进的萤火虫算法(improved firefly algorithm,IFA)和差分布谷鸟搜索算法(differential evolution cuckoo search algorithm,DCSA),发现依据这2种算法的寻优结果制定的系统运行策略比其他算法的能耗更低;ZHENG等[10-11]提出的改进杂草入侵优化算法(improved invasive weed optimization,EIWO)和改进人工鱼群算法(improved artificial fish swarm algorithm,IAFSA)也是解决此问题的有效方法;TEIMOURZADEH等[12]将增广群搜索优化算法(augmented group search optimization,AGSO)应用于该目标的求解,发现AGSO算法具有良好收敛性,能取得良好的节能效果;于军琪等[1]提出一种改进的烟花算法(improved fireworks algorithm,IFA),相比于现有的优化结果,该算法能够找到更好的运行策略,同时在收敛性方面具有较强竞争性。
从以上研究可以看出,数学规划求解方法和元启发式算法能从中央空调系统运行实际情况出发解决OCL问题,并且具有较好优化效果。但是,大部分元启发式算法都是在集中搜索环境下搜索求解,搜索过程相较于并行式搜索过程较慢,并且需要较大的种群规模。此外,一个优化算法可能在一个优化问题上有较好性能,但在其他优化问题上并不适用。特别是对OCL问题,并联冷机系统由不同性能和容量的冷机组成,并且不同系统中冷机数量也不同,导致该问题中优化变量维度、适应度函数不确定。因此,研究一种适用范围更广、稳定性更强、不需针对特定优化问题的并行式搜索算法十分重要。
COUCEIRO等[13]提出分数阶达尔文粒子群优化(fractional order Darwinian particle swarm optimization, FODPSO)算法,该算法以一种并行式搜索方式寻优,对计算问题要求低且搜索效率较高;荣兵等[14-15]分别在该算法中利用Logistic模型和粒子状态信息动态调整分数阶次,能显著提高收敛精度和速度。近年来,FODPSO算法在其他领域也有着众多应用,例如红外图像分割和缺陷边缘识别[16]、血管的边缘检测[17]和可持续绿色能源系统的控制[18]。综上所述,FODPSO算法对于优化问题的求解有着显著的效果,因此,本文应用该算法解决OCL问题。
1 问题描述
中央空调系统采用的多冷机系统可以调整本身的负荷,使每台冷机都运行在最佳工况下。图1所示为多冷机系统结构图,由图1可见:多冷机系统由2台或多台冷机通过并联或串联管道连接到一个共同的分配系统[9],这导致该系统具有操作灵活性较高、备用容量较大和中断维护较少的特点。该系统可以通过调整本身的运行工况满足末端的基本负荷需求,使其以最佳效率运行。
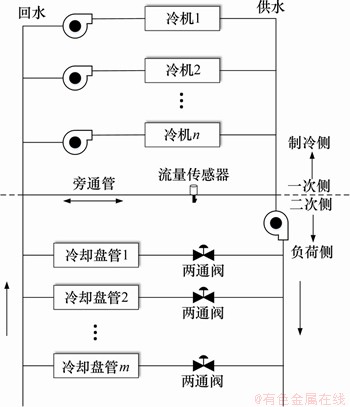
图1 多冷机系统结构图
Fig. 1 Systematic diagram of multiple-chiller plant
每台冷机都有不同的额定容量和能耗特征,供水和回水可以通过旁通管调节,使水流量可根据系统的末端负荷需求进行变化。通过控制供回水的水流量,系统的末端负荷需求可以分配到每1台冷机,满足整个系统的负荷需求。多冷机系统在中央空调方面具有较稳定的控制效果。
典型OCL问题的优化目标通常表示为整个冷机系统的功率消耗,具体而言,是在满足末端负荷需求的前提下,使各冷机的能耗总和达到最小,获得最佳系统性能,达到节能减排的目的。在一定的湿球温度下,离心式冷水机组的功率是其部分负荷率的凸函数[2]。本文将离心式冷水机组的功耗表示为
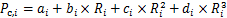 (1)
(1)
式中: 为第i台冷机功率,ai,bi,ci和di为第i台冷机本身的性能参数;Ri为第i台冷机的部分负荷率。
为第i台冷机功率,ai,bi,ci和di为第i台冷机本身的性能参数;Ri为第i台冷机的部分负荷率。
并联冷机系统负荷分配问题是在给定目标函数最小的情况下,寻找不超过运行限制条件的冷水机组部分负荷率,以最低运行功率满足中央空调末端负荷需求,如下式所示:
 (2)
(2)
式中:P为并联冷机系统的总功率;Np为并联冷机台数。考虑到冷水机组的性能和制造厂商的建议,每台冷机的部分负荷率R应不小于0.3。
因此,并联冷机负荷分配优化模型的目标函数和约束条件的数学式如下:
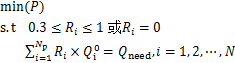 (3)
(3)
式中: 为第i台冷水机组的额定制冷量;Qneed为系统末端冷却负荷需求。
为第i台冷水机组的额定制冷量;Qneed为系统末端冷却负荷需求。
2 改进分数阶达尔文粒子群优化算法
PSO算法是用于优化问题最著名的生物启发算法之一,是受鸟群在二维空间觅食启发得来的[6],但最大的问题是容易陷入局部最优,降低算法的求解精度。FODPSO算法首先将PSO算法扩展到多个种群协同进化,增强种群多样性[19];其次,将参数选择任务复杂化,通过达尔文选择机制动态改变各种群的种群规模和搜索空间对优化问题进行求解,包括删除最差粒子、生成新粒子和新种群,这种动态改变种群规模可以合理分配计算资源[20]。
假设问题维数为D,算法中每个粒子代表在搜索空间中的1个可行解,速度 和位置
和位置 表示粒子i当前的运动状态,适应度反映粒子的优劣。在粒子速度中引入分数阶微积分使粒子在运动过程中表现得更平滑和智能[14],使某一时刻粒子的速度包含与当前和过去时间相关的项:
表示粒子i当前的运动状态,适应度反映粒子的优劣。在粒子速度中引入分数阶微积分使粒子在运动过程中表现得更平滑和智能[14],使某一时刻粒子的速度包含与当前和过去时间相关的项:

 (4)
(4)
式中: 为分数阶系数。
为分数阶系数。
虽然FODPSO算法的收敛精度较PSO算法有了较大提升,但粒子同样只学习个体最优和全局最优的更新方式,依旧使算法陷入局部最优值的概率较大。另一方面,FODPSO算法必须依据粒子整体评价性能,这种随机性进化无法保证粒子所有维同时趋向最优[21],影响算法的稳定性和收敛速度。
针对上述问题,提出了一种改进的分数阶达尔文粒子群优化(improved fractional order Darwinian particle swarm optimization,IFODPSO)算法。改进算法的主要作用有:
1) 采用蒙特卡洛方法结合基本算数运算符生成初始种群,可以在搜索前期加快粒子逼近较好的搜索区域,提高前期收敛速度;
2) 引入多重优化改进粒子性能的评判方式,对所有粒子各维的值逐维更新并比对适应度,提高算法稳定性并加快收敛进程;
3) 在此基础上,提出在粒子位置更新时通过自适应多策略行为使并行种群的所有粒子依适应度自适应选择更新方式,从而更好地平衡全局勘探和局部开发能力,最终提高算法的搜索精度。
该算法求解OCL问题时,待优化目标为并联冷机系统总功率最小,待优化变量为各冷机的部分负荷率(R),末端负荷需求作为约束条件。针对并联冷机负荷分配问题,其求解过程的具体步骤如下。
2.1 初始化
粒子的初始位置通常是随机的,理想情况下与全局最优解无关。但针对不同的优化问题,算法的收敛精度和速度对其初始值有不同程度的依赖性[22]。当初始值偶然接近全局最优解时,可以减少搜索量,快速逼近全局最优解。
蒙特卡洛是一种依赖重复随机抽样获取数值结果的方法。重复模拟的次数越多,数值结果越逼近问题的解,同时,问题的维数对蒙特卡洛的计算量不造成影响。因此,初始化时,利用蒙特卡洛方法可以快速找到全局最优解的近似解 ,为后续寻优提供一个更精确的搜索空间。
,为后续寻优提供一个更精确的搜索空间。
结合基本算数运算符即四则运算所使用的运算符来生成初始种群:除法和乘法运算符分别提供长距离和短距离搜索,加法和减法运算符提供中等距离搜索[19]。用式(5)定义初始化粒子:

 (5)
(5)
式中:N0为各并行种群的初始种群规模; 为随机数,
为随机数, ;Xj为近似最优解对应维的值;
;Xj为近似最优解对应维的值;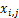 为粒子初始位置,表示第i个粒子在j维搜索空间的分量。
为粒子初始位置,表示第i个粒子在j维搜索空间的分量。
OCL问题中部分负荷率是连续变化的,设定由并联冷机系统的部分负荷率序列组成的向量表示每个粒子的位置,即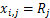 ,因此,每一个粒子都代表OCL问题的1个可行解。同时必须满足冷机部分负荷率的预定义范围,
,因此,每一个粒子都代表OCL问题的1个可行解。同时必须满足冷机部分负荷率的预定义范围,
 (6)
(6)
通过基本算术运算符建立近似最优解和随机数的运算关系,可以较全面地将粒子生成在距近似解较近、较远和中等距离的区域,同时,式(5)保证所有粒子的初始化位置集中在近似最优解周围。图2所示为改进前后种群初始化位置示意图。这种直接将粒子生成在最优解附近的初始化方式可以减少搜索可行域,提高粒子前期的搜索效率。
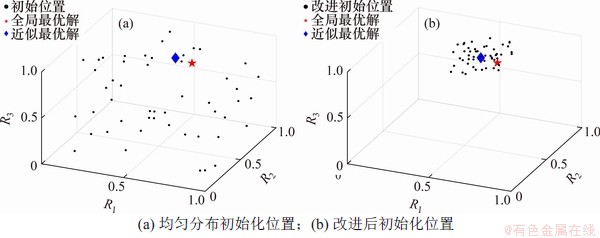
图2 改进前后种群初始化位置示意图
Fig. 2 Schematic diagram of population initialization position before and after improvement
粒子过大的初始速度容易使粒子超出搜索空间的边界,影响算法收敛速度。本文将粒子速度初始化为0,如式(7)所示,其中vi,j(0)为粒子初始速度:
 (7)
(7)
为了初始化各并行种群中粒子的个体最优和全局最优并量化每个粒子的价值,将粒子适应度 表示为
表示为
 (8)
(8)
其中: 为粒子i对应的冷水机组总功率。
为粒子i对应的冷水机组总功率。
2.2 多重优化
FODPSO算法在求解OCL问题时使所有冷机对应的部分负荷率序列同时计算和更新,而这会导致整体较差粒子的某些维可能比整体较好粒子的对应维更好,却不能体现在个体最优中用于更新[21]。因此,搜索出各冷机的最优部分负荷率十分困难,同时会使各维变量相互影响进而出现震荡现象,影响算法稳定性[23]。
本文将1次迭代过程分割为更小的间隔,每个间隔只更新一部分负荷率序列,依次完成所有部分负荷率序列的更新。
1) 从 开始更新,保持所有粒子中除
开始更新,保持所有粒子中除 外的其余R对应维的值不变,对与R1对应维的值、个体最优和全局最优进行更新;
外的其余R对应维的值不变,对与R1对应维的值、个体最优和全局最优进行更新;
2) 只对R2对应维的值进行更新并更新个体最优和全局最优;
3) 依次更新所有R对应维的值,依达尔文选择机制进化种群,即一次迭代过程结束,进入下一次迭代,直至达到终止迭代的条件为止。
多重优化改进粒子优劣的评判方式:更新 时使用的个体最优和全局最优相较于更新Rj时拥有更好的价值,保证粒子在迭代过程中具有更好的价值。同时,每台冷机的部分负荷率序列单独更新消除了变量之间的相互影响,提高了算法的稳定性。
时使用的个体最优和全局最优相较于更新Rj时拥有更好的价值,保证粒子在迭代过程中具有更好的价值。同时,每台冷机的部分负荷率序列单独更新消除了变量之间的相互影响,提高了算法的稳定性。
2.3 自适应多策略行为
粒子的速度和位置更新是本算法的核心内容,但传统仅通过学习其个体最优和全局最优来更新,这会造成算法全局勘探和局部开发能力不平衡,使陷入局部最优的概率增大。为了解决该问题,本文在粒子位置更新时引入自适应多策略行为:将各并行种群中的粒子依适应度分为精英粒子和次等粒子,不同类型的粒子自适应地选择各自的更新方式,分别用于局部开发和全局勘探。
精英粒子适应性较好,其主要任务是通过局部开发提高搜索精度,定义其学习样本集由各并行种群的所有精英粒子组成;次等粒子适应性较差,其主要任务是通过全局勘探保持种群多样性,定义其学习样本集由各并行种群的所有粒子组成。图3所示为自适应学习策略。由图3可见:各粒子依据其适应度自适应选择更新方式更新自身位置,同时,达尔文选择机制使各并行种群在更新过程中可以通过删除最差粒子、生成新粒子和生成新种群,动态改变种群规模和搜索空间。
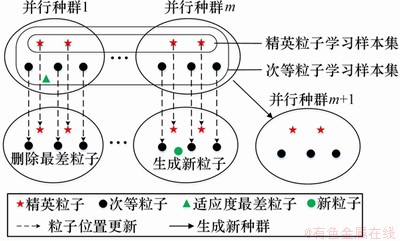
图3 自适应学习策略
Fig. 3 Adaptive learning strategies
2.3.1 维度学习
通过粒子的个体最优向全局最优学习,维度学习重新构造个体最优,可以将全局最优中有价值的信息传递给个体最优[24]。本文采用基于多重优化的维度学习更新精英粒子,假设以5台并联冷机总能耗最低为优化目标,如图4所示。其中, ,是精英粒子i的个体最优;
,是精英粒子i的个体最优; ,是精英粒子学习样本集中的全局最优,两者各维度的值分别用于对应冷机部分负荷率序列的更新,多重优化导致Rj更新完毕后更新
,是精英粒子学习样本集中的全局最优,两者各维度的值分别用于对应冷机部分负荷率序列的更新,多重优化导致Rj更新完毕后更新 ,
, 用于Rj+1的更新。同时,设置1个测试向量
用于Rj+1的更新。同时,设置1个测试向量 ,具体过程如下。
,具体过程如下。
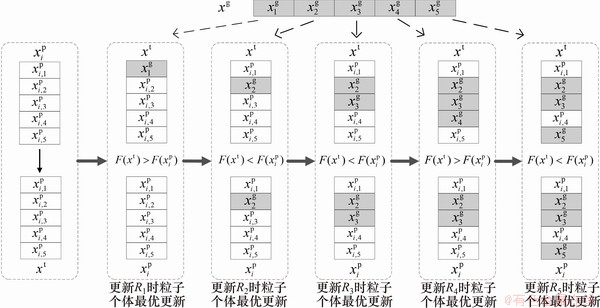
图4 维度学习更新精英粒子i
Fig. 4 Dimensional learning updates elite particle i
step 1:首先令 ,对于
,对于 ,使
,使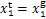 ,则
,则 ,适应度
,适应度 ,因此,
,因此, 不更新,比较各精英粒子适应度并更新
不更新,比较各精英粒子适应度并更新 。
。
step 2:令 ,对于
,对于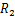 ,使
,使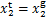 ,
, ,因此,更新
,因此,更新 ,
, ,更新
,更新 ;
;
step 3:令 ,对于
,对于 ,使
,使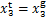 ,
,  ,因此,更新
,因此,更新 ,
,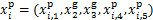 ,更新
,更新 ;
;
step 4:令 ,对于
,对于 ,使
,使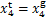 ,
,  ,因此,
,因此, 不更新,更新
不更新,更新 ;
;
step 5:令 ,对于
,对于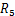 ,使
,使 ,
,  ,因此,更新
,因此,更新 ,
, ,更新
,更新 。
。
精英粒子i更新Rj时公式如下:
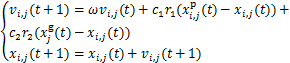 (9)
(9)
式中: 为惯性权重;学习因子c1和c2为非负常数;r1和r2为
为惯性权重;学习因子c1和c2为非负常数;r1和r2为 之间的随机数。维度学习中所有精英粒子都从全局最优中学习来完成位置的更新,这种以全局最优为中心的信息交流方式使其具有强大的局部开发能力[24],同时,多重优化保证了每个精英粒子在迭代过程中具有更好的价值。
之间的随机数。维度学习中所有精英粒子都从全局最优中学习来完成位置的更新,这种以全局最优为中心的信息交流方式使其具有强大的局部开发能力[24],同时,多重优化保证了每个精英粒子在迭代过程中具有更好的价值。
2.3.2 遗传学习
KAO等[25]证明GA由于遗传算子在进行交叉和变异时的相对无方向性,该算法的局部开发能力较差但具有较强的全局勘探能力。因此,将次等粒子看作遗传算子,采用基于多重优化的遗传学习来更新次等粒子,提高算法的全局勘探能力。具体步骤如下。
1) 交叉。更新 时,首先将次等粒子i的个体最优
时,首先将次等粒子i的个体最优 和次等粒子学习样本集中的全局最优
和次等粒子学习样本集中的全局最优 对应维的值进行交叉,产生后代
对应维的值进行交叉,产生后代
 。
。
 (10)
(10)
式中:粒子m为次等粒子学习样本集中的任一粒子,随机数 。
。
2) 变异。随后后代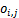 以概率pm发生变异,各维都会生成1个随机数
以概率pm发生变异,各维都会生成1个随机数 。
。
 (11)
(11)
式中: 和
和 为
为 预定义范围的边界。
预定义范围的边界。
3) 选择。经过交叉和变异产生的后代 与次等粒子i当前的学习样本即个体最优
与次等粒子i当前的学习样本即个体最优 的适应度进行比较,得到次等粒子i最终的学习样本
的适应度进行比较,得到次等粒子i最终的学习样本 :
:
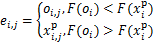 (12)
(12)
采用文献[27]提出的粒子速度更新方式,次等粒子学习样本集中所有粒子的个体最优都可用于更新粒子速度,该样本集的设置也有利于加快次等粒子向所有并行种群中的优秀个体学习,保留了种群的多样性。次等粒子i更新 时公式如下:
时公式如下:
 (13)
(13)
遗传学习应用遗传算子,通过交叉、变异和选择重新构造学习样本以更新次等粒子。交叉集成了个体最优和全局最优的信息,可以产生价值更高的后代;变异通过对后代信息的随机性更改使次等粒子具有较强的全局勘探能力;确保次等粒子的学习样本随着迭代进行拥有更好的价值。同样地,多重优化使更新Rj后更新个体最优和全局最优并使两者在更新Rj+1时的交叉和选择阶段发挥作用,保证每个次等粒子在迭代过程中具有更好的价值。
在每一次迭代过程中,各并行种群中的粒子都会根据适应度重新分类,之后重新自适应选择更新方式来满足不同的搜索目的。因此,不仅同一个种群中的不同粒子在1次迭代过程中有不同的更新方式,而且同一个粒子在不同的迭代过程中也有不同的更新方式。区别于魏博文等[26]提出的PSO-GA算法,2种算法松散耦合导致相互作用产生的效果难以确定,自适应多策略行为动态地为不同状态的粒子提供不同的更新方式并使粒子分别专注于全局勘探和局部开发,提高了算法性能[20]。
2.4 迭代选择
采用搜索计数器 来记录种群中粒子在迭代过程中未找到更好全局最优的次数[18]。若
来记录种群中粒子在迭代过程中未找到更好全局最优的次数[18]。若 达到
达到 ,则删除该种群中适应度最低的粒子;当生成1个新粒子时,
,则删除该种群中适应度最低的粒子;当生成1个新粒子时, 将被重置为0。为了保持算法搜索多样性,每次删除粒子后
将被重置为0。为了保持算法搜索多样性,每次删除粒子后 随被删除粒子数目Nkill更新:
随被删除粒子数目Nkill更新:
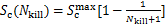 (14)
(14)
每个并行种群在没有粒子被删除的前提下,都可以采用式(15)生成1个新种群,以此避免持续产生新种群,造成种群数量过快达到上限。
 (15)
(15)
式中:随机数 [
[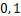 ];ng为该并行种群的种群规模。
];ng为该并行种群的种群规模。
FODPSO算法的收敛性能直接取决于分数阶系数 [16],更新公式如下:
[16],更新公式如下:
 (16)
(16)
其中:t为当前迭代次数;T为设定的总迭代次数。
IFODPSO算法在求解OCL问题时的流程如图5所示。
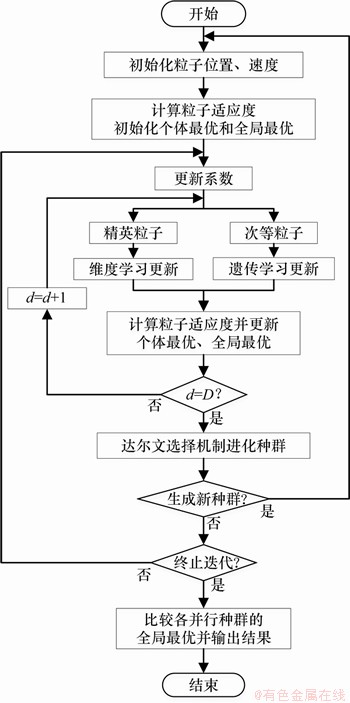
图5 IFODPSO算法流程图
Fig.5 Flow chart of IFODPSO algorithm
2.5 时间复杂度分析
定义N和D为种群规模和问题维数,PSO算法的时间复杂度为O(N×D)[24];FODPSO算法中各并行种群的时间复杂度计算如下。
1) 初始化:O(N×D);
2) 粒子进行速度与位置更新:O(2N×D);
3) 达尔文选择机制进化种群:2×O(1)+O(lgN);
4) 计算粒子适应度:O(N×D);
5) 判断迭代是否停止:O(1)。
IFODPSO算法由于对初始化和粒子更新方式进行了改进,使算法时间复杂度有所增加:初始化过程时间复杂度变为O(NM)+O(N×D)(NM为蒙特卡洛模拟次数)、粒子速度与位置更新时间复杂度变为O(N1×D)+2×O(N2×D)+O(1)+O(N×D)(N1和N2分别为精英粒子和次等粒子的个数),但与基本FODPSO算法的时间复杂数在同一个数量级。这表明IFODPSO算法的较高收敛精度、较快收敛速度和较好稳定性是以牺牲较少计算复杂度为代价获得的[16]。
3 测试案例与结果分析
3.1 测试案例
选取2个典型的并联冷机系统验证IFODPSO算法性能。案例1的系统由3台制冷量为2 813.6 kW的冷机组成;案例2的系统则由4台制冷量4 501.8 kW和2台4 396.3 kW的冷机组成。2个案例中的并联冷机系统均位于中国台湾省新州科学园区的半导体工厂,并相继被用于测试PSO[6],DE[2],DCSA[9],EIWO[10]和IFA[1]等相关优化算法求解OCL问题的能力。2个案例中的并联冷机系统具有不同数量和制冷量的冷机就是为了测试IFODPSO算法在不同并联冷机系统和不同工况下解决OCL问题的能力。系统中部分冷机的类型和额定制冷量都是相同的,但由于各冷机经过长时间运行后设计温度和流量等均存在差异,导致各冷机的性能曲线并不相同,因此,各冷机的性能参数a,b,c和d也不相同。在2个案例中,冷水机组的性能参数如表1所示。
表1 并联冷机系统中各设备性能参数
Table 1 Performance parameters of each device in parallel chiller system

3.2 结果分析
为了验证IFODPSO算法求解OCL问题的可行性,对该算法与其他现有优化算法在每个实验工况下分别进行独立实验,并将经过相同次数迭代后得到的结果进行对比。在案例1的实验中,将IFODPSO算法与GA[5]、PSO[6]和DCSA[9]算法的优化结果进行对比,结果如表2所示。从表2可见:与GA算法相比,IFODPSO算法在不同负荷需求(占系统总额定制冷功率的比例)下相对节能比例可以达到0.20%~21.66%,特别是当负荷需求低于60%时,节能效果更加明显,达到了11.49%~21.66%;IFODPSO算法与PSO和DCSA算法在各负荷需求下得到的计算结果相似。
在案例2的实验中,将IFODPSO算法与GA[5]、PSO[6]和DS[28]算法的优化结果进行对比,如表3所示。从表3可见:与GA算法相比,IFODPSO算法在不同负荷需求下相对节能比例可以达到0.59%~4.51%,与PSO算法相比节能0.02%~2.71%,特别是当负荷需求低于75%时,所得的运行策略相较于GA和PSO算法都具有更明显的节能效果;而与DS算法相比,在负荷需求高于80%时,优化效果相当,负荷需求小于75%时,节能1.62%~2.24%,整体上具有较好节能效果。
表2 案例1中GA、PSO、IFA、IFODPSO算法结果对比
Table 2 GA, PSO, IFA, IFODPSO algorithm results comparison in Case 1

表3 案例2中GA、PSO、DS、IFODPSO结果对比
Table 3 GA, PSO, DS, IFODPSO algorithm results comparison in Case 2

同时,将IFODPSO算法与FODPSO[13]、TSLPSO[24]算法优化结果进行对比,如表4所示。从表4可见:案例1中,IFODPSO算法在各负荷需求下均有与FODPSO和TSLPSO算法相当的节能效果;案例2中,IFODPSO算法在不同负荷需求下相对节能比例可以达到0.02%~4.85%。相比于案例1,案例2中IFODPSO算法的节能效果更加明显。这是因为系统中冷机数量更多,对应优化问题的维数更高,进一步说明IFODPSO算法在解决高维优化问题时具有更大优势。值得注意的是,案例2中FODPSO算法的优化结果明显低于其他算法的优化效果,主要原因是FODPSO算法搜索到次优解时直接放弃该区域的搜索而开始搜索另一个新的区域,导致搜索效率低,使算法需要很长的收敛时间,在规定迭代次数内无法收敛,而改进之后的IFODPSO算法使搜索能力得到提升。
表4 不同案例中FODPSO、TSLPSO、IFODPSO算法优化总功率对比
Table 4 Comparison of optimization total power of FODPSO, TSLPSO and IFODPSO in different cases

在2个案例实验中,IFODPSO算法的收敛曲线如图6所示。由图6可见:在算法执行过程中,在迭代初期适应度快速下降,之后较平稳,说明算法在满足系统末端负荷需求的前提下向总功率最小的方向迭代更新。案例1中,算法在20次之前完成了迭代收敛过程;案例2中,算法在30次之前完成了迭代收敛过程,具有良好的收敛性。同时,收敛前期曲线较平缓,说明改进后的初始化使算法从全局最优解附近开始寻优,加快了算法前期收敛速度。
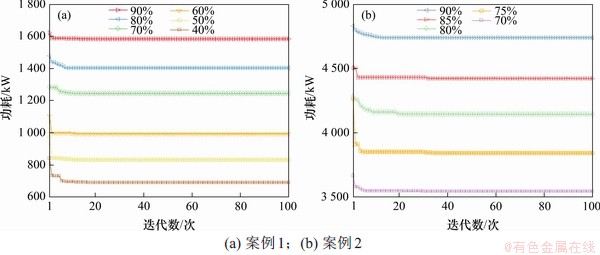
图6 不同案例下IFODPSO算法收敛曲线
Fig. 6 Convergence curves of IFODPSO algorithm under different cases
根据上述实验结果可见,除了案例2中在负荷需求小于75%工况下IFODPSO算法的计算结果明显优于TSLPSO外,其他情况下优化结果均相同或相近。为了消除偶然性并进一步检验算法的稳定性,IFODPSO算法和TSLPSO算法在各负荷需求下,迭代次数为100次,独立运行30次的计算结果的平均值、最小值、最大值和标准差如表5所示。
表5 IFODPSO算法与TSLPSO算法优化结果对比
Table 5 Comparison of optimization results between TSLPSO and IFODPSO

由表5可见:案例1中2种算法在各负荷需求下计算结果的标准差均保持较低水平,尤其当负荷需求低于60%时,IFODPSO算法所得结果的标准差为0,TSLPSO算法所得结果的标准差相较于该算法在其他工况下更接近于0,说明2种算法对于案例1等较低维度的优化问题均有较好稳定性。案例2中IFODPSO算法所得结果标准差均不超过0.01,明显比TSLPSO算法的低,特别是当负荷需求分别为70%和75%时标准差为0;而TSLPSO算法在各负荷需求下所得结果的标准差较大,特别是当负荷需求为70%,80%,85%和90%时标准差分别达到了28.353 1,2.777 1,5.239 1和7.399 3,远远高于相同工况下IFODPSO算法所得结果的标准差,说明对于案例2等高维优化问题IFODPSO算法有更好稳定性。另外,2个案例中不同负荷需求下IFODPSO算法计算总功率的最小值、最大值和平均值均比TSLPSO算法的低,同时验证了IFODPSO算法的优越性。
另外,TSLPSO算法和IFODPSO算法在各负荷需求下30次计算结果与最优值的相对误差如图7所示。从图7可见:对于案例1,TSLPSO算法相对误差均低于0.015%,其中负荷需求为40%和50%工况下的相对误差曲线较平坦;而IFODPSO算法相对误差均低于0.004%,其中负荷需求为40%,50%和60%工况下的相对误差曲线很平坦且接近于0。
对于案例2,TSLPSO算法相对误差均低于5%,其中负荷需求为75%工况下的相对误差曲线较平坦;而IFODPSO算法相对误差均低于6×10-5,其中负荷需求为70%和75%工况下的相对误差曲线很平坦且接近于0。同时,IFODPSO算法在2个案例中的其余工况下相对误差曲线虽有波动,但相对于TSLPSO算法来说均保持很低水平。因此,从整体上看,IFODPSO算法得到的各工况下30次运行结果的相对误差曲线比TSLPSO算法更平坦,相对误差更小,验证了算法的稳定性。
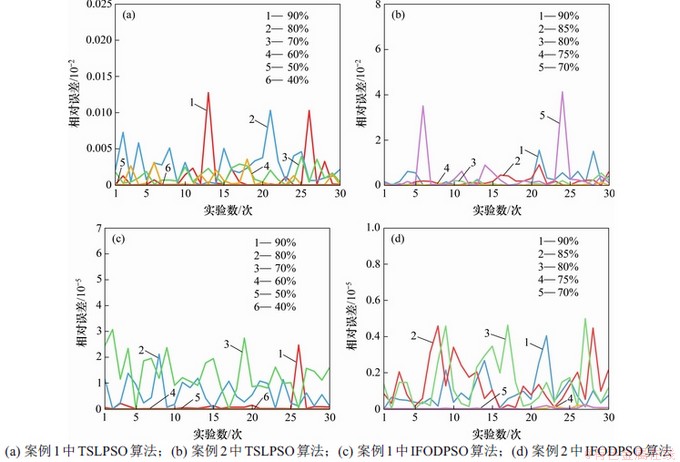
图 7 不同案例下TSLPSO和IFODPSO算法相对误差
Fig.7 Relative error of TSLPSO and IFODPSO algorithm under different cases
4 结论
1) 针对并联冷机负荷分配(OCL)问题,建立了并联冷机负荷分配优化模型,提出了一种改进分数阶达尔文粒子群优化(IFODPSO)算法来求解OCL问题。
2) 算法中引入蒙特卡洛方法结合基本算数运算符,减少搜索可行域;采用多重优化策略削弱各维变量之间的相互影响,利于同时搜寻到每一维最优解;在粒子进行更新时采用自适应多策略行为使每个粒子依据自身性能动态选择更新方式,平衡算法的全局勘探和局部开发能力。
3) IFODPSO算法在收敛精度、收敛速度和稳定性方面的综合性能相较于现有优化算法显著提升,改进效果明显,能使并联冷机系统中的各冷机按能耗更低的运行策略运行。
4) IFODPSO算法是一种有效解决OCL问题的算法。在未来的研究工作中,将重点研究多目标IFODPSO算法及其在整个冷冻站系统中的多目标优化问题中的应用。
参考文献:
[1] 于军琪, 王福, 赵安军, 等. 基于改进烟花算法的并联冷机负荷分配优化研究[J/OL]. 控制与决策: 1-10[2021-04-28].
YU Junqi, WANG Fu, ZHAO Anjun, et al. Load distribution optimization of parallel chiller based on improved fireworks algorithm[J/OL]. Control and decision making, 1-10[2021-04-28].
[2] LEE W S, CHEN Yi-Ting, KAO Yucheng. Optimal chiller loading by differential evolution algorithm for reducing energy consumption[J]. Energy and Buildings, 2011, 43(2/3): 599-604.
[3] CHANG Y C. A novel energy conservation method—optimal chiller loading[J]. Electric Power Systems Research, 2004, 69(2/3): 221-226.
[4] CHANG Y C, CHAN T S, LEE W S. Economic dispatch of chiller plant by gradient method for saving energy[J]. Applied Energy, 2010, 87(4): 1096-1101.
[5] CHANG Y C. Genetic algorithm based optimal chiller loading for energy conservation[J]. Applied Thermal Engineering, 2005, 25(17/18): 2800-2815.
[6] LEE W S, LIN L C. Optimal chiller loading by particle swarm algorithm for reducing energy consumption[J]. Applied Thermal Engineering, 2009, 29(8/9): 1730-1734.
[7] CHANG Y C, CHEN W H, LEE C Y, et al. Simulated annealing based optimal chiller loading for saving energy[J]. Energy Conversion and Management, 2006, 47(15/16): 2044-2058.
[8] COELHO L D S, MARIANI V C. Improved firefly algorithm approach applied to chiller loading for energy conservation[J]. Energy and Buildings, 2013, 59: 273-278.
[9] COELHO L D S, KLEIN C E, SABAT S L, et al. Optimal chiller loading for energy conservation using a new differential cuckoo search approach[J]. Energy, 2014, 75: 237-243.
[10] ZHENG Zhixin, LI Junqing. Optimal chiller loading by improved invasive weed optimization algorithm for reducing energy consumption[J]. Energy and Buildings, 2018, 161: 80-88.
[11] ZHENG Zhixin, LI Junqing, DUAN Peiyong. Optimal chiller loading by improved artificial fish swarm algorithm for energy saving[J]. Mathematics and Computers in Simulation, 2019, 155: 227-243.
[12] TEIMOURZADEH H, JABARI F, MOHAMMADI-IVATLOO B. An augmented group search optimization algorithm for optimal cooling-load dispatch in multi-chiller plants[J]. Computers & Electrical Engineering, 2020, 85: 106434.
[13] COUCEIRO M S, ROCHA R P, FERREIRA N M F, et al. Introducing the fractional-order Darwinian PSO[J]. Signal, Image and Video Processing, 2012, 6(3): 343-350.
[14] 荣兵, 陈华. Logistic型混合自适应分数阶达尔文粒子群优化算法[J]. 计算机测量与控制, 2017, 25(8): 221-225.
RONG Bing, CHEN Hua. Logistic-model hybrid adaptive fractional order Darwinian partical swarm optimization algorithm[J]. Computer Measurement & Control, 2017, 25(8): 221-225.
[15] 郭通, 兰巨龙, 李玉峰, 等. 自适应的分数阶达尔文粒子群优化算法[J]. 通信学报, 2014, 35(4): 130-140.
GUO Tong, LAN Julong, LI Yufeng, et al. Adaptive fractional-order Darwinian particle swarm optimization algorithm[J]. Journal on Communications, 2014, 35(4): 130-140.
[16] TANG Qingju, GAO Shuaishuai, LIU Yongjie, et al. Infrared image segmentation algorithm for defect detection based on FODPSO[J]. Infrared Physics & Technology, 2019, 102: 103051.
[17] WANG Yuanyuan, PENG Wenxian, QIU Chen-Hui, et al. Fractional-order Darwinian PSO-based feature selection for media-adventitia border detection in intravascular ultrasound images[J]. Ultrasonics, 2019, 92: 1-7.
[18] JASMINE G M A, AGEES K C, GNANA S A. Iot based sustainable wind green energy for smart cites using fuzzy logic based fractional order Darwinian particle swarm optimization[J]. Measurement, 2020, 166: 108208.
[19] WANG Zijia, ZHAN Zhihui, YU Weijie, et al. Dynamic group learning distributed particle swarm optimization for large-scale optimization and its application in cloud workflow scheduling[J]. IEEE Transactions on Cybernetics, 2019, 50(6): 2715-2729.
[20] WEI Bo, XIA Xuewen, YU Fei, et al. Multiple adaptive strategies based particle swarm optimization algorithm[J]. Swarm and Evolutionary Computation, 2020, 57: 100731.
[21] 田瑾. 高维多峰函数的量子行为粒子群优化算法改进研究[J]. 控制与决策, 2016, 31(11): 1967-1972.
TIAN Jin. Improvement of quantum-behaved particle swarm optimization algorithm for high-dimensional and multi-modal functions[J]. Control and Decision, 2016, 31(11): 1967-1972.
[22] LI Qian, LIU Sanyang, YANG Xinshe. Influence of initialization on the performance of metaheuristic optimizers[J]. Applied Soft Computing, 2020, 91: 106193.
[23] CHEN Jiayu, SUN Yongjun. A new multiplexed optimization with enhanced performance for complex air conditioning systems[J]. Energy and Buildings, 2017, 156: 85-95.
[24] XU Guiping, CUI Quanlong, SHI Xiaohu, et al. Particle swarm optimization based on dimensional learning strategy[J]. Swarm and Evolutionary Computation, 2019, 45: 33-51.
[25] KAO Y T, ZAHARA E. A hybrid genetic algorithm and particle swarm optimization for multimodal functions[J]. Applied Soft Computing, 2008, 8(2): 849-857.
[26] 魏博文, 徐镇凯, 李火坤, 等. 基于GA-APSO混合罚模型的混凝土坝力学参数优化反演[J]. 中南大学学报(自然科学版), 2015, 46(11): 4211-4217.
WEI Bowen, XU Zhenkai, LI Huokun, et al. Optimization inversion for mechanical parameters of concrete dam based on GA-APSO mixed penalty model[J]. Journal of Central South University(Science and Technology), 2015, 46(11): 4211-4217.
[27] LIANG Jing, QIN Kai, SUGANTHAN P N, et al. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J]. IEEE Transactions on Evolutionary Computation, 2006, 10(3): 281-295.
[28] SULAIMAN M H, IBRAHIM H, DANIYAL H, et al. A new swarm intelligence approach for optimal chiller loading for energy conservation[J]. Procedia-Social and Behavioral Sciences, 2014, 129: 483-488.
(编辑 秦明阳)
收稿日期: 2021-01 -15; 修回日期: 2021 -03 -20
基金项目(Foundation item):国家重点研发计划项目(2017YFC0704100);安徽建筑大学智能建筑与建筑节能安徽省重点实验室2018年度开放课题 (IBES2018KF08) (Project(2017YFC0704100) supported by the National Key Research and Development Program of China; Project(IBES2018KF08) supported by the Anhui Jianzhu University Intelligent Building and Building Energy Saving Anhui Key Laboratory Opening Project in 2018)
通信作者:赵安军,博士,副教授,从事智能建筑暖通空调控制与优化研究;E-mail:zhao_anjun@163.com
DOI: 10.11817/j.issn.1672-7207.2021.06.020
引用格式:于军琪, 赵泽华, 赵安军, 等. 求解并联冷机负荷分配问题的改进FODPSO算法[J]. 中南大学学报(自然科学版), 2021, 52(6): 1901-1914.
Citation:YU Junqi, ZHAO Zehua, ZHAO Anjun, et al. Improved FODPSO algorithm for load distribution of parallel chillers[J]. Journal of Central South University(Science and Technology), 2021, 52(6): 1901-1914.