J. Cent. South Univ. (2018) 25: 131-140

DOI: https://doi.org/10.1007/s11771-018-3723-x

Three-dimensional land FD-CSEM forward modeling using edge finite-element method

LIU Jian-xin(柳建新)^{1, 2}, LIU Peng-mao(刘鹏茂)^{1, 2}, TONG Xiao-zhong(童孝忠)^{1, 2}

1. School of Geosciences and Info-physics, Central South University, Changsha 410083, China;

2. Hunan Key Laboratory of Non-ferrous Resources and Geological Hazard Exploration,Changsha 410083, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: A modeling tool for simulating three-dimensional land frequency-domain controlled-source electromagnetic surveys, based on a finite-element discretization of the Helmholtz equation for the electric fields, has been developed. The main difference between our modeling method and those previous works is edge finite-element approach applied to solving the three-dimensional land frequency-domain electromagnetic responses generated by horizontal electric dipole source. Firstly, the edge finite-element equation is formulated through the Galerkin method based on Helmholtz equation of the electric fields. Secondly, in order to check the validity of the modeling code, the numerical results are compared with the analytical solutions for a homogeneous half-space model. Finally, other three models are simulated with three-dimensional electromagnetic responses. The results indicate that the method can be applied for solving three-dimensional electromagnetic responses. The algorithm has been demonstrated, which can be effective to modeling the complex geo-electrical structures. This efficient algorithm will help to study the distribution laws of 3-D land frequency-domain controlled-source electromagnetic responses and to setup basis for research of three-dimensional inversion.

Key words: three-dimensional model; frequency-domain electromagnetic method; horizontal electric dipole; forward modeling; edge finite-element

Cite this article as: LIU Jian-xin, LIU Peng-mao, TONG Xiao-zhong. Three-dimensional land FD-CSEM forward modeling using edge finite-element method [J]. Journal of Central South University, 2018, 25(1): 131–140. DOI: https://doi.org/10.1007/s11771-018-3723-x.

1 Introduction

The frequency-domain controlled-source electromagnetic method has long been widely used in a wide range of geophysical research such as mineral exploration [1], hydrocarbon exploration [2] and crustal studies [3]. Moreover, the interpretations of the frequency-domain controlled- source electromagnetic data in complex geological environments increasingly resort to multidimensional inverse modeling. Because forward modeling is a major numerical bottleneck for the inverse modeling, it is important to develop efficient and accurate forward modeling algorithms.

Calculation of electromagnetic responses for three-dimensional model of the subsurface must be relied on numerical methods. These numerical solutions are obtained by approximating the relevant differential or integral equations and solving a matrix equation. For the frequency- domain controlled-source electromagnetic forward modeling, three methods have been used most for this approximation, namely, integral equation methods, finite-difference methods and finite- element methods. Initially, integral equation methods received the most attention [4–7]. These methods are applied to anomalous conductivity in a simple geological setting. The integral equation methods are very accurate but the computation burden increases thus are usually used to modeling the effects of simple three-dimensional models. As computer speed and memory increased, finite- difference methods also received more attention [8–13]. However, the finite-difference methods require discretization of the whole three- dimensional domain. Recently, finite-element methods have received increasing attention [14–19]. The finite-element methods are attractive because they are supposed to be more apt to complex geometries than other methods.

However, the traditional node finite-element methods did not work well due to spurious solutions. Moreover, the node finite-element methods did not satisfy the condition that the product of permittivity and electric field have zero divergence throughout source-free regions [19]. Thus, the edge finite-element method is put forward for solving the land frequency-domain controlled- source electromagnetic forward problem.

The main difference between our modeling method and those previous works is that our edge finite-element approach is applied to solve the three-dimensional land frequency-domain electromagnetic responses generated by horizontal electric dipole source. Firstly, the edge finite- element equation is formulated through using the Galerkin method based on Helmholtz equation of the electric fields. Secondly, in order to check the validity of the modeling code, the numerical results are compared with the analytical solutions for a homogeneous half-space model. Finally, another three models are simulated with three-dimensional electromagnetic responses.

2 Forward modeling

2.1 Governing equations

The earth model and the measurement configuration considered in our work is shown in Figure 1. The horizontal electric dipole source is placed parallel to the x-axis, and the receivers measuring the electric field in x-direction and magnetic field in y-direction are assumed to be on the earth’s surface and on the x–y plane.

Assuming a time harmonic dependence of e^–iωt, the first-order Maxwell’s equations in frequency domain can be expressed as

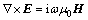                           (1)

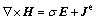                          (2)

where E is the electric field intensity in V/m; H is the magnetic field intensity in A/m; J^e is the electric current density of the source in A/m²; ω is the angular frequency; σ and μ₀ (4π×10^–7 H/m) are the electrical conductivity and magnetic permeability, respectively.

It is obtained from Eqs. (1) and (2) that a second-order vector Helmholtz equation for E or H can be obtain as

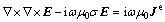                 (3)

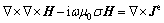                 (4)

Solving the coupled system of Eqs. (1) and (2) requires substantial computer memory. The memory requirement can be reduced by about half when solving either Eqs. (3) or (4). When the electric- field formulation (see Eq. (3)) is adopted, magnetic fields are then computed directly from Eq. (2).

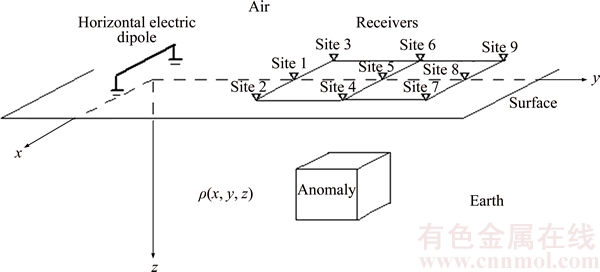
Figure 1 Coordinate system for three-dimensional forward modeling (The horizontal electric dipole source is situated on the earth surface and the electromagnetic parameter ρ or σ vary in the x-, y-, z-direction)

Similarly, when the magnetic-field formulation (see Eq. (4)) is solved, electric fields are derived from Eq. (1). E and H obtained from Eqs. (1) and (3) are theoretically identical to those from Eqs. (2) and (4).

2.2 Discretization using edge finite-element

To solve the governing differential Eq. (3) using an edge finite-element method, we divide a computing domain into homogeneous hexahedral elements capable of modeling irregular geometries. A tangential component of the electric field is assigned to each edge of the distorted brick element (Figure 2). Within an eth element, the unknown electric field, E^e, can be approximated as

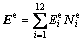                            (5)

where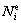and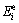denote the linear edge interpolation function and the tangential electric field on the ith edge of the element, respectively.

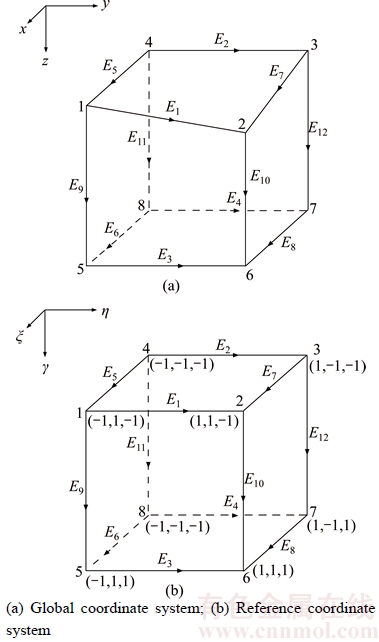
Figure 2 Edge elements designed for electric fields:

To construct these edge basis functions, a coordinate transformation is used to map a hexahedral element in the (x,y,z)-coordinate system into a cubic element in a new (ξ, η, γ)-coordinate system (Figure 2). The required transformation can easily be found to be

                      (6)

where

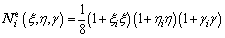        (7)

with (ξ_i, η_i, γ_i) denoting the coordinates of the ith node.

To construct four edge basis functions for the edges parallel to the ξ-axis, let us define those faces for which ξ is constant. On the faces, 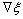possesses only a normal component since the faces are perpendicular to the ξ-axis. Functions defined by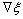therefore have non-zero tangential components only along the edges parallel to the ξ-axis since ξ varies linearly along the edges and is constant on the other edges. By using the node- based scalar function in a hexahedral element given by Eq. (7), the corresponding edge basis functions are built for those edges as [20]

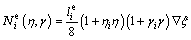             (8)

where 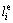is the length of the ith edge. Similarly, the edge basis functions are constructed for edges parallel to the η-axis as

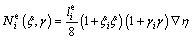             (9)

and for edges parallel to the γ-axis as

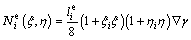             (10)

Since the edge basis functions satisfy a constant tangential component along the associated edge and no tangential components along the other edges, the expansion in Eq. (3) guarantees the continuity of the tangential electric field, conserving the continuity of a current, which allows the discontinuity of normal electric fields, at an inter–element boundary. The edge finite-element method satisfying the boundary condition can therefore effectively suppress the spurious solutions, while conventional node-based finite-element methods not satisfying the condition achieve the same objective by introducing a penalty factor in the finite-element formulation [9].

With the discretization and interpolation described above, using the Galerkin method a discrete form of Eq. (3) is obtained. The resulting element equation is in matrix form, A^ex^e=b^e, where a component of A^e is expressed as

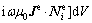                       (11)

To calculate Eq. (11) numerically, we express it in the (ξ, η, γ)-coordinate system using the coordinate transformation in Eq. (6). It can be rewritten as

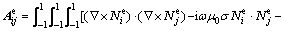
               (12)

where |Jac| denotes the determinant of the Jacobian matrix, given by

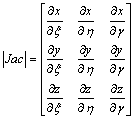                    (13)

Assembling all element equations in a computing domain with the Dirichlet boundary condition, we can find the system of equations, Ax=b, where A is a symmetrical sparse complex matrix [9], x is a vector that represents the unknown electric field at each edge and b is the source vector that depends on the Dirichlet boundary condition.

Once the electric fields at the earth’s surface are known, then magnetic fields at the surface are determined by the integral form of Eq. (1). So, the apparent resistivity ρ_xy can be calculated as

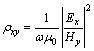                         (14)

2.3 Solving system of equations

The system of equations that result from a finite-element approximation over a three- dimensional grid can be solved using Krylov space iterative methods because a direct solution requires prohibitive amounts of memory and computation. The convergence of Krylov space methods depends on the condition number of the system matrix and on the clustering property of the eigenvalues. Convergence is greatly accelerated by applying an appropriate pre-conditioner, e.g., utilizing LU or Cholesky factorizations [21–23]. The bi-conjugate gradient stabilized method, or BiCGSTAB proposed by Van der Vorst is used, combined with a symmetric successive over relaxation (SSOR) for our problem.

Following SAAD [21], of the incomplete Cholesky factorization used in this paper is given as

1     U(1,:)=A(1,:)

2     for i=2:n

3      row=A(i,:);

4      for k=1:(i–1) and row(k)_=0

5       row(k)=row(k)/U(k,k)

6        Apply a dropping rule to vector row.

7        if (row(k)≠0)

8     row(k+1:n)=row(k+1:n)–row(k)*U(k,k+1:n)

9        end

10     end

11     U(i,i:n)=row(i:n)

12     end

In line 6, an element row(k) is dropped (i.e., replaced by zero) if it is less than the relative tolerance τi obtained by multiplying the drop tolerance by the two-norm of the ith row of matrix A.

2.4 Validity test of forward modeling algorithm

In order to test the forward modeling algorithm, the code is applied to a homogeneous half-space. For a nonmagnetic homogeneous half-space, the analytical response of the horizontal electric dipole source can be expressed as [22]

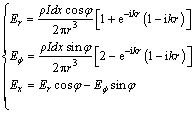           (15)

and

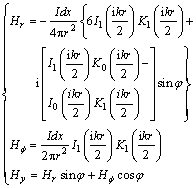           (16)

where K₀ and K₁ are the modified Bessel functions of the second kind of order 0 and 1.

Consider a homogeneous half-space of 100 Ω·m, and the source is a x-directed horizontal electric dipole located at the earth surface y=0 m. The finite element responses along the y-axis are shown in Figrue 3 at 100 Hz. The finite element method responses are in good agreement with the analytical responses which validate the forward modeling.

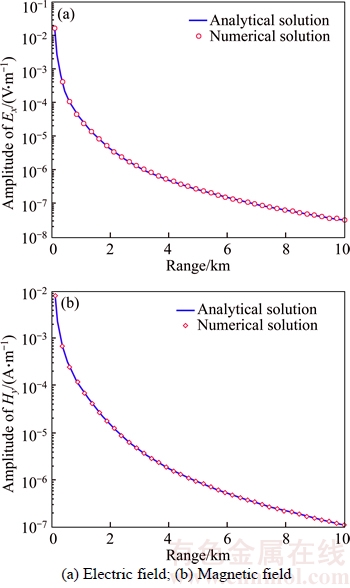
Figure 3 Comparison of numerical response and analytical (solid line) solution measured on surface of 100 W×m half-space:

3 Numerical results

3.1 Model 1: A conductive cubic body embedded in homogeneous half-space

Model 1 consists of a homogeneous half-space with resistivity of 100 Ω·m, containing a conductive cubic body with the resistivity of 10 Ω·m. The cubic body has a side of 400 m and is located at a depth of 200 m, as shown in Figure 4.

The electromagnetic field in this model is generated by a horizontal (x-oriented) electric dipole transmitter with a length of 1000 m and located at (x,y)=(0, –6000) m. The transmitter generates the electromagnetic field with transmitting current of 1 A at 10 Hz. Note that, in practice, the transmitting current may be equal to 100–1000 A. However, the observed data are usually normalized by the transmitter current.

The electromagnetic responses have been computed for this model in 441 receivers located at every 100 m in the x- and y-direction on 21×21 grid at the surface. Figure 5 shows the three-dimensional electromagnetic responses at 10 Hz for the Model 1. The synthetic components of the electric and magnetic field at the surface have totally different anomaly patterns: the electric magnetic is anomalous above the target and the magnetic field changes sign from the near panel to the far. There is little compelling evidence to indicate a conductive body at depth, never mind trying to infer information directly concerning the conductivity contrast and buried depth. In Figure 5, the apparent resistivity (ρ_xy) can reflect the location and size of the conductive body. Therefore, the apparent resistivity can be used as a qualitative analysis parameter for the three-dimensional anomalous of land frequency-domain controlled-source electromagnetic method.

So far, a relatively simple model has been dealt with. Although the results are promising, it gives only a first indication of the reliability and stability of the method. Hence, more complicated situations are studied below.

3.2 Model 2: Two conductive cubic bodies embedded in a homogeneous half-space

Figure 6 shows a sketch of Model 2 selected for this modeling experiment. Two conductive cubic bodies are embedded in a homogeneous half-space.

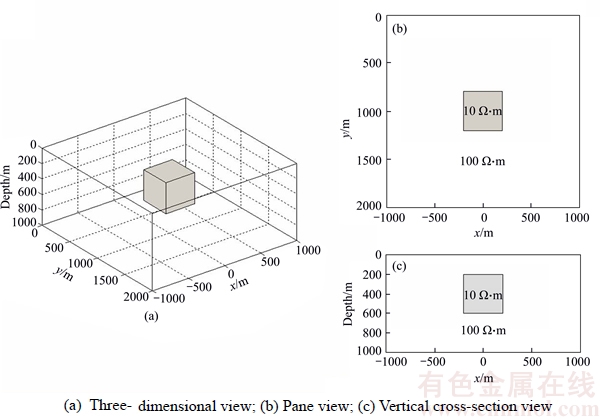
Figure 4 A sketch of Model 1 of a conductive cubic body embedded in a homogeneous half-space:

Figure 5 Three-dimensional electromagnetic responses computed at 10 Hz for Model 1 shown in Figure 4:

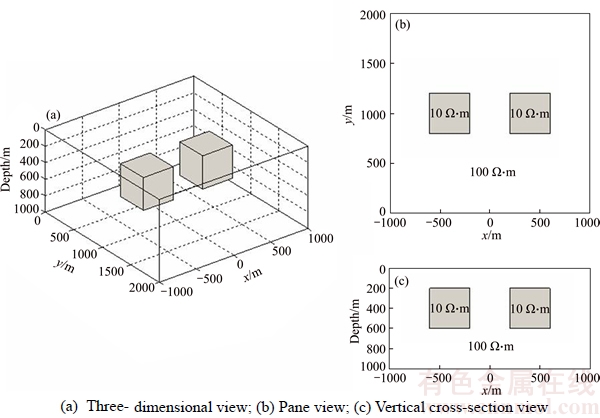
Figure 6 Sketch of Model 2 of two conductive cubic bodies embedded in homogeneous half-space:

The resistivity of the bodies is 10 Ω·m and that of the homogenous background is 100 Ω·m. The cubic bodies have a side of 400 m. They are located at a depth of 200 m below the surface at a distance of 400 m, one from another.

Similarly, the electromagnetic field in this model is generated by a horizontal electric dipole transmitter with a length of 1000 m and located at (x,y)=(0, –6000) m. The transmitter generates the electromagnetic field with transmitting current of 1 A at 10 Hz and 100 Hz.

The electromagnetic responses have been computed for this model in 441 receivers located at every 100 m in the x- and y-direction of a 21×21 grid at the surface. Figrue 7 shows the three- dimensional electromagnetic responses at 10 Hz and 100 Hz for the Model 2. In Figure 7, the apparent resistivity (ρ_xy) can reflect the location and size of the two conductive bodies.

3.3 Model 3: Conductive and resistive cubic bodies embedded in a homogeneous half-space

Figure 8 shows a sketch of Model 3 selected for this modeling experiment. The conductive and resistive cubic bodies are embedded in a homogeneous half-space. The resistivity of the conductive body is 10 Ω·m, the resistivity of the resistive body is 1000 Ω·m and that of the homogenous background is 100 Ω·m. The cubic bodies have a side of 400 m. They are located at a depth of 200 m below the surface at a distance of 400 m, one from another, as shown in Figure 8.

Also, the electromagnetic field in this model is generated by a horizontal electric dipole transmitter with a length of 1000 m and located at (x,y)=(0, –6000) m. The transmitter generates the electromagnetic field with transmitting current of 1 A at 10 Hz and 100 Hz.

The electromagnetic responses have been computed for this model in 441 receivers located at every 100 m in the x- and y-direction of a 21×21 grid at the surface. Figure 9 shows the three- dimensional electromagnetic responses at 10 Hz and 100 Hz for the Model 3. In Figure 9, the apparent resistivity (ρ_xy) can reflect the location and size of the conductive body, but the resistive cubic body cannot be reflected. Therefore, the responses can be known on an anomalous body underground that the land frequency-domain controlled-source electromagnetic method reflects ore or mineral with low resistivity better than the one with high resistivity.

4 Conclusions

1) A edge finite-element algorithm for simulating three-dimensional land frequency-domain electromagnetic responses generated by horizontal electric dipole source is presented. The algorithm can eliminate the spurious solutions and can guarantee electric field have no zero divergence throughout source-free regions.

Figure 7 Three-dimensional electromagnetic responses computed for Model 2 shown in Figure 6:

Figure 8 Sketch of Model 3 of conductive and resistive cubic bodies embedded in a homogeneous half-space:

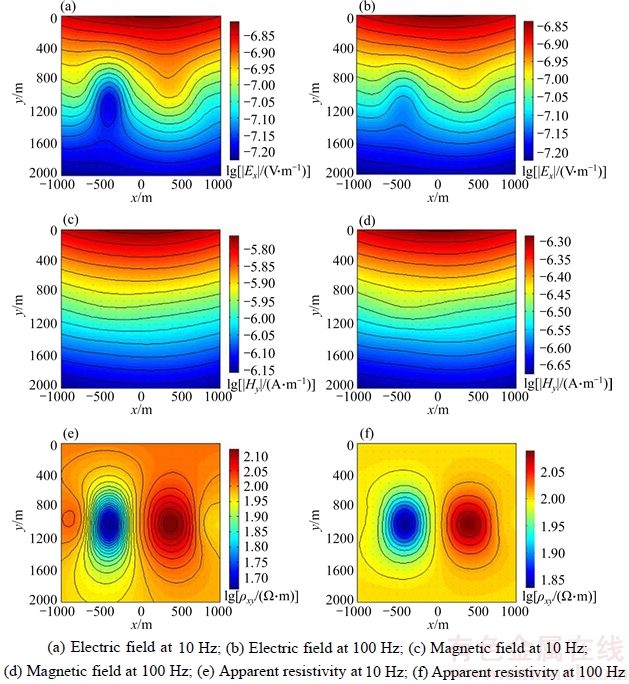
Figure 9 Three-dimensional electromagnetic responses computed for Model 3 shown in Figure 8:

2) The system of equations of the edge finite- element algorithm is a large sparse, banded, symmetric, ill-conditioned, and non-Hermitian complex matrix equation. Then, the bi-conjugate gradient stabilized method combined with a symmetric successive over relaxation (SSOR) was appled for solving the equations.

3) The validity of this algorithm is confirmed by comparing modeling results with synthetic results. This efficient algorithm will help to study the distribution laws of 3-D land frequency-domain controlled-source electromagnetic responses and to setup basis for research of three-dimensional inversion.

References

[1] WHITE D, BOERNER D, WU J, LUCAS S, BERRER E, HANNILA J, SOMERVILLE R. Mineral exploration in the Thompson nickel belt, Manitoba, Canada, using seismic and controlled-source EM methods [J]. Geophysics, 2000, 65(6): 1871–1881.

[2] CONSTABLE S, SRNKA L J. Special section-marine controlled-source electromagnetic methods an introduction to marine controlled-source electromagnetic methods for hydrocarbon exploration [J]. Geophysics, 2007, 72(2): WA3– WA12.

[3] MACGREGOR L, SINHA M, CONSTABLE S. Electrical resistivity structure of the Valu Fa Ridge, Lau Basin, from marine controlled-source electromagnetic sounding [J]. Geophysical Journal International, 2001, 146(1): 247–236.

[4] AVDEEV D B, KUVSHINOV A V, PANKRATOV O V, NEWMAN G A. Three-dimensional induction logging problems, Part 1: An integral equation solution and model comparisons [J]. Geophysics, 2002, 67(2): 413–426.

[5] HURSAN G, ZHDANOV M S. Contraction integral equation method in 3-D electromagnetic modeling [J]. Radio Science, 2002, 37(6): 1089.

[6] LIU Jian-xin, JIANG Peng-fei, TONG Xiao-zhong, XU Ling-hua, XIE Wei, WANG Hao. Application of BICGSTAB algorithm with incomplete LU decomposition preconditioning to two-dimensional magnetotelluric forward modeling [J]. Journal of Central South University: Science and Technology, 2009, 40(4): 485–490. (in Chinese)

[7] ZHDANOV M S, LEE S K, YOSHIOKA K. Integral equation method for 3Dmodeling of electromagnetic fields in complex structures with inhomogeneous background conductivity [J] Geophysics, 2006, 71(6): G333–G345.

[8] HABER E, ASCHER U, ARULIAH D, OLDENBURG D. Fast simulation of 3D electromagnetic problems using potentials [J]. Journal of Computational Physics, 2000, 163(1): 150–171.

[9] HAN N, NAM M J, KIM H J, SONG Y, SUH J H. A comparison of accuracy and computation time of three- dimensional magnetotelluric modelling algorithms [J]. Journal of Geophysics and Engineering, 2009, 6(2): 136–145.

[10] MEHANEE S, ZHDANOV M. A quasi-analytical boundary condition for three-dimensional finite difference electromagnetic modeling [J]. Radio Science, 2004, 39(6): RS6014.

[11] NEWMAN G A, ALUMBAUGH D L. Frequency-domain modeling of airborne electromagnetic responses using staggered finite differences [J]. Geophysical Prospecting, 1995, 43(8): 1021–1042.

[12] STREICH R. 3D finite-difference frequency-domain modeling of controlled-source electromagnetic data: Direct solution and optimization for high accuracy [J]. Geophysics, 2009, 74(5): F95–F105.

[13] WEISS C J, CONSTABLE S. Mapping thin resistors and hydrocarbons with marine EM methods, part II-modeling and analysis in 3D [J]. Geophysics, 2006, 71(6): G321–G332.

[14] BRNER R U, ERNST O G, AND SPITZER K. Fast 3-D simulation of transient electromagnetic fields by model reduction in the frequency domain using Krylov subspace projection [J]. Geophysical Journal International, 2008, 173(3): 766–780.

[15] da SILVA N V, MORGAN J V, MACGREGOR L, WARNER M. A finite element mutifrontal method for 3D CSEM modeling in the frequency domain [J]. Geophysics, 2012, 77(2): E101–E115.

[16] MUKHERJEE S, EVERETT M E. 3Dcontrolled-source electromagnetic edge-based finite element modeling of conductive and permeable heterogeneities [J]. Geophysics, 2011, 76(4): F215–F226.

[17] NAM M J, KIM H J, SONG Y, LEE T J, SON J S, SUH J H. 3D magnetotelluric modelling including surface topography [J]. Geophysical Prospecting, 2007, 55(2): 277–287.

[18] UM E, HARRIS J M, ALUMBAUGH D L. 3D time-domain simulation of electromagnetic diffusion phenomena: A finite- element electric-field approach [J]. Geophysics, 2010, 75(4): F115–F126.

[19] FARQUHARSON C G, MIENSOPUST M P. Three- dimensional finite-element modelling of magnetotelluric data with a divergence correction [J]. Journal of Applied Geophysics, 2011, 75(4): 699–710.

[20] JIN J M. The finite element method in electromagnetics [M]. 2nd ed. New York: John Wiley & Sons, 2002.

[21] SAAD Y. Iterative methods for sparse linear systems [M]. 2nd ed London: Cambridge University Press, 2002.

[22] KAUFMAN A A, KELLER G V. Frequency and Transient Soundings (Methods in Geochemistry and Geophysics) [M]. Elsevier Science Press, 1983.

[23] CAI Hong-zhu, XIONG Bin, MICHAEL Z. Three- dimensional marine controlled-source electromagnetic modeling in anisotropic medium using finite element method [J]. Chinese Journal of Geophysics, 2015, 58(8): 2839–2850. (in Chinese)

(Edited by HE Yun-bin)

中文导读

陆地频率域可控源电磁法三维矢量有限元正演

摘要：大规模三维电磁数据的定量解释需要发展高效、稳定的三维正反演算法。正演是反演的前提和基础，本文对正演问题开展深入研究，实现了适用于陆地电磁勘探的频率域可控源电磁三维正演。首先，基于麦克斯韦方程组推导得到关于电场的亥姆霍兹方程，通过伽辽金法建立了基于棱边元的有限元方程。控制方程经过矢量有限元离散化后得到大型、对称、稀疏复线性方程组，为了实现高效求解该线性方程组，选用了不完全Cholesky分解预处理的迭代解法进行求解。其次，通过对均匀半空间模型的矢量有限元模拟计算，数值结果与解析解的对比验证了本文算法的正确性。最后，对电性三维地电模型进行数值模拟，计算的电磁响应均能反应出异常体的存在，进一步说明本文算法能够对频率域可控源电磁三维进行有效模拟。因此，本文矢量有限元算法的成功实现可用于三维电磁响应的分析计算，并有助于研究陆地三维频率域可控源电磁响应的分布规律，同时也能为三维频率域可控源电磁法反演研究奠定基础。

关键词：三维模型；频率域电磁法；水平电偶源；正演模拟；矢量有限元

Foundation item: Projects(41674080, 41674079) supported by the National Natural Science Foundation of China

Received date: 2016-03-30; Accepted date: 2017-12-01

Corresponding author: TONG Xiao-zhong, PhD, Associate Research Fellow; Tel: +86–18874896727; E-mail: csumaysnow@163.com; ORCID: 0000-0001-8641-9360