复合型超声马达纵向振动建模

易幼平, 钟 掘

(中南大学 机电工程学院, 湖南 长沙, 410083)

摘要: 针对采用一维理论模型在研究复合型超声马达振动特性时分析结果出现误差的情况, 设计一种新型双定子复合型超声马达; 利用马达的对称性建立了定子纵向振动分析物理模型; 将定子纵向与横向振动的动能同时引入Hamilton方程, 推导了考虑马达横向振动效应的定子纵向振动分析微分方程与动力边界条件; 运用Maple软件对定子运动微分方程进行求解, 获得了定子纵向振动固有频率; 采用有限元模型与一维理论模型对定子的纵向振动固有频率进行对比计算, 并对马达原型机的固有频率进行测定。 研究结果表明: 所建模型比一维理论模型具有更高的分析精度; 分析结果与实验值及有限元计算值吻合。
关键词: 超声马达; 压电陶瓷; 固有频率; 纵向振动; 横向振动
中图分类号:TM356 文献标识码:A 文章编号: 1672-7207(2005)03-0452-06

Modeling of longitudinal vibration of hybrid ultrasonic motor

YI You-ping, ZHONG Jue

(School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

Abstract: One-dimensional model will lead to analytical error when the vibration characters of hybrid ultrasonic motor are considered. A new type of hybrid ultrasonic motor with 2 stators was developed. Considering the symmetrical properties of this motor, a physical model for longitudinal vibration analysis of the stator was established. By introducing the kinetic energy of the vibrations in longitudinal and transversal directions into the Hamilton equation, the differential equation for longitudinal vibration analysis and the dynamical boundary conditions were deduced, in which the transversal vibration effect was considered. The Maple software was used to solve these differential equations and the eigenfrequency of longitudinal vibration for the stator was obtained. For the purpose of comparison with the refined theoretical model, a finite element model and a one-dimensional model were used to compute the eignefrequency of longitudinal vibration. Furthermore, the eignefrequency of this motor prototype was measured in the experiment. The research results show that the theoretical model proposed has much higher accuracy than one-dimensional model. The analytical results agree well with the experimental results and the calculted results obtained by the finite element method.
Key words: ultrasonic motor; piezoceramic; eigenfrequency; longitudinal vibration; transversal vibration 

超声马达是一种利用压电陶瓷的逆压电效应实现机电能量转换的新型马达, 由于它具有低速大扭矩、 响应快、 控制特性好、 不受磁场影响及运动准确等优良性能, 在航空航天、 机器人、 微型机械和自动控制等领域具有广阔的应用前景^[1-3]。

复合型超声马达是一个纵、扭复合朗之万振动系统, 由纵向与切向压电陶瓷(PZT)振子组成, 2个振子在定子中分别激发2个正交的振动模态, 其中切向PZT振子使定子产生扭转振动模态, 通过定、 转子间的摩擦力驱动转子运动; 纵向PZT振子产生轴向振动模态, 控制定、 转子间的摩擦力, 将双向扭转振动转换为转子的单向运动^[4,5]。 由于复合型超声马达比行波型超声马达具有更大的输出力矩和更好的低速稳定性, 自发明以来在超声马达研究领域受到国内外学者的普遍关注^[6-13]。 然而, 复合型超声马达只有10多年的发展历史, 马达设计理论体系还不完善, 目前建立的纵向振动分析模型都基于一维理论, 马达截面的横向变形被忽略^[14-18]。 事实上, 复合型超声马达已不再只是细长杆, 不符合一维理论的适用条件, 因此, 复合型超声马达纵向振动分析理论模型尚待进一步研究。 为此, 作者设计了一种双定子复合型超声马达, 其工作原理与S.Ueha等设计的单定子复合型超声马达相似^[2], 不同的是作者提出的复合型马达含有2个定子, 且在定子上设计了2个支撑环。 针对采用一维理论模型分析复合型超声马达纵向振动中存在的问题, 利用马达的对称性建立定子纵向振动分析的物理模型; 根据Hamilton原理推导考虑马达横向振动效应的定子纵向振动分析的微分方程与动力边界条件; 采用有限元模型与一维理论模型对定子的固有频率进行计算, 并对马达原型机的固有频率进行测试。

1 纵向振动物理模型与材料本构方程

双定子复合型超声马达为对称结构, 转子的厚度较薄, 定子纵向振动物理模型的边界可视为一端固定、 一端自由。 由于定子中激发的纵、 扭振动相互解耦, 纵向振动物理模型可用图1表示。其中,u_i为局部坐标z_i方向的位移。

由线性压电理论可知, 以应变S和电场强度E为自变量的纵向振动型PZT材料的本构方程为:

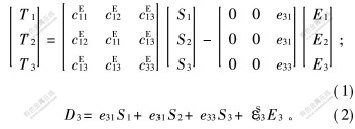
其中: T_i为应力分量; S_i为应变分量; D_i为电位移分量; c^E_ij为恒定电场下的弹性常数; e_ij为压电应力常数; ε^S_ij为恒定应变下的介电常数。

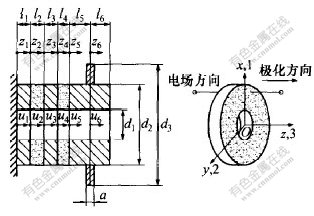
图 1   定子纵向振动分析物理模型
Fig. 1   Physical analysis model of longitudinal
vibration of stator  

忽略径向应力, 即T₁=T₂=0, 则式(1)和(2)变为:

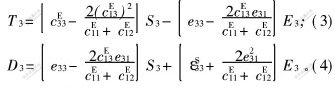
进一步简化得到纵向振动型PZT材料的本构方程为:

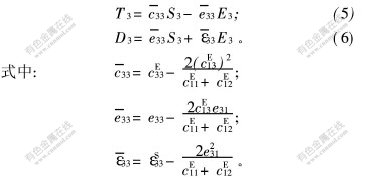
在分析纵向振动时, 厚度切变振动型PZT沿轴向的应力为:

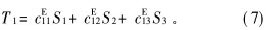
对于厚度切变振动型PZT, 同样假设T₂=T₃=0, 得到下列关系式:

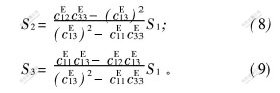
将方程(8)和(9)代入方程(7)得:

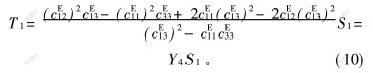
其中: Y₄为厚度切变振动型PZT的弹性模量。

2 纵向振动分析理论模型

2.1 纵向振动微分方程的通解形式

根据纵向振动分析物理模型(图1), Hamilton方程具有以下形式:

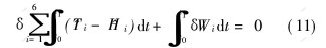
其中: [AKT^]_i为系统的动能; [AKH^]_i为系统的焓; δW_i为外界对系统做的虚功。

一维理论只考虑了材料的轴向变形, 当定子横截面较大时, 为获得精确的振动分析理论模型, 应考虑其径向变形。 由图1所示的坐标系可知, 定子内任意一点的速度矢量可表示为:

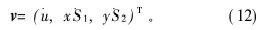
其中: u表示位移; (˙)表示对时间求导。

若S₁=S₂, 则系统的动能表达式为:

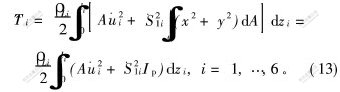
其中: I_p为极惯性矩; A为定子横截面积; ρ_<sub>Li为定子材料的质量密度。 引入回转半径i_p,据I_p=i²_pA, 方程(13)可进一步简化为:

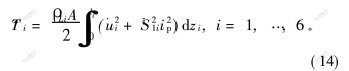
根据材料本构方程(1), (2)以及纵向振动分析物理模型, 考虑马达横向变形效应的系统动能关系式如下。

对纵向振动型PZT,有:

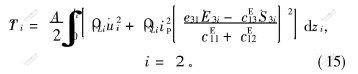
对其他材料,有:

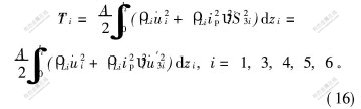
其中: υ_i为泊松比; (′)表示对坐标的偏导数。

纵向振动型PZT的焓为:

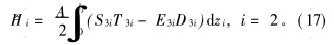
将材料本构方程(3)及(4)代入式(17), 得:

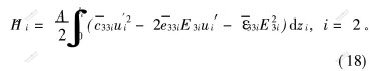
弹性材料与扭振型PZT的焓为:

在短路条件下, 外界对系统所做的虚功δW_i=0。

将能量方程(15), (16), (18)及(19)代入Hamilton方程(11)并整理得:

根据方程(20),可得到定子纵向振动微分方程为:

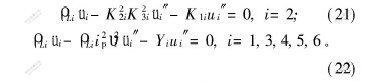
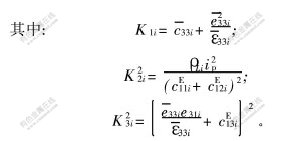
在谐波激励下, 可引入分离变量形式:u(z,t)=U(z)·e^jΩt,E₃(z,t)=E₃(z)·e^jΩt,φ(t)=φ·e^jΩt,D₃(t)=D₃·e^jΩt,代入方程(21)和(22)得:

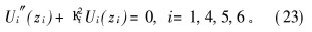
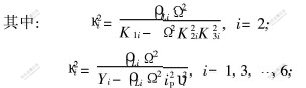
Ω为角频率。

方程(23)的通解形式为:

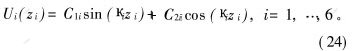
其中: C_1i和C_2i为待定积分常数, 由马达的边界条件和连续性条件确定。

2.2 边界条件

由定子振动分析物理模型可知, 马达纵向振动边界条件为一端固定、 一端自由, 因此,存在以下关系式:

U₁(0)=0;(25)
U₆′(l₆)=0。(26)

根据连续性条件, 在截面z₁=l₁, z₂=l₂, z₃=l₃, z₄=l₄和z₅=l₅处, 位移满足下列方程:

U_i(l_i)=U_i+1(0), i=1,…,5。(27)

在截面z₅=l₅处, 由于增加了调整环, 附加的质量m将使该截面沿轴向的受力F发生变化, 环的宽度在分析中被忽略, 看作集中质量。 其受力分析如图2所示。

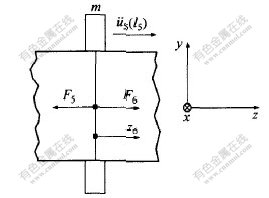
图 2   截面z₅=l₅的动力边界条件
Fig. 2   Dynamical boundary condition on
cross section z₅=l₅

由牛顿定律可得截面z₅=l₅处的动力连续条件为:

Y₅AU₅′(l₅)-Y₆AU₆′(0)=mΩ²U₅(l₅)。(28)

由方程(20)得到如下定子各截面的动力连续条件。

a. 在区域1和2的连接处:

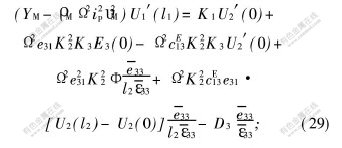
b. 在区域3和4的连接处:

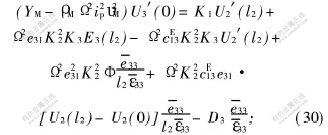
c. 在区域4和5的连接处:

(YM-ρMΩ²i²pυ²M)U₃′(l₃)=(Y₄-ρ₄Ω²i²pυ²₄)U₄′(0);(31)

d. 在区域4和5的连接处:

(YM-ρMΩ²i²pυ²M)U₅′(0)=(Y₄-ρ₄Ω²i²pυ²₄)U₄′(l₄)。(32)

其中:Y_M表示弹性材料的弹性模量; υ_M为弹性材料的泊松比; ρ_M为弹性材料的质量密度。

方程(24)有12个积分常数, 可通过12个边界条件方程(25), (26), (27)(含5个边界条件方程), (28), (29), (30), (31)和(32)求解。

3 纵向振动固有频率分析

将上述纵向振动微分方程通解代入连续性条件与动力边界条件, 可得到纵向振动微分方程组的表达形式:
AC=r。(33)
其中: A为系数矩阵; C为积分常数矩阵; C=(C₁₁, C₁₂, C₂₁, C₂₂, …, C₆₁, C₆₂); r为外力矩阵。

方程(33)具有非零解的必要条件为:
det(A)=0。(34)

方程(34)即为纵向振动频率方程, 通过该方程可以对双定子复合型马达进行振动分析与结构参数优化。 将定子的材料参数(表1)代入纵向振动频率方程, 利用Maple软件求解该矩阵方程。

为验证纵向振动模型的精确度, 分别采用一维理论模型、 有限元模型对定子纵向振动进行理论计算,同时对马达样机进行实验研究, 测定了定子的纵向振动频率。 其对比分析结果如图3所示。

采用本文的精确模型计算得到的第一阶固有频率为20.5 kHz, 实验测试值为19.48 kHz, 有限元计算值为20.75 kHz, 一维理论模型的计算结果为22.8kHz。 显然, 在建模过程中,由于考虑了定子的横向变形,模型计算值与实际结果更为接近。 本文建立的定子纵向振动分析理论模型的精度高于一维理论模型, 其分析结果与实验数据以及有限元结果吻合。

表 1   马达材料参数
Table 1   Material parameters of motor

 1—实验结果; 2—精确模型结果;
3—有限元模型结果; 4—一维理论模型结果
图 3   纵向振动一阶固有频率理论分析结果
与实验结果
Fig. 3   Analysis and experiment results for the
first order eigenfrequency of longitudinal vibration

4 结 论

a. 利用所提出的复合型超声马达的对称性以及纵、 扭振动解耦的特点, 建立了定子纵向振动分析物理模型与边界条件。

b. 将定子纵向与横向振动的动能同时引入Hamilton方程, 推导了考虑马达横向振动效应的定子纵向振动分析理论模型, 运用Maple软件对定子振动分析理论模型进行求解。

c. 所建立的理论模型比一维理论模型具有更高的分析精度, 分析结果与实验值及有限元计算值吻合。

参考文献:

[1]Sashida T, Kenjo T. An introduction to ultrasonic motors[M]. Oxford: Clarendon Press, 1993.
[2]Ueha S, Tomikawa Y. Ultrasonic motors——theory and applications[M]. Oxford: Clarendon Press, 1993.
[3]Wallaschek J. Piezoelectric ultrasonic motors[J]. Journal of Intelligent Material Systems and Structures, 1995,6(1): 71-83.
[4]Nakamura K, Kurosawa M, Ueha S. Design of a hybrid transducer type ultrasonic motor[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 1993, 40(4): 395-401.
[5]Nakamura K, Kurosawa M, Ueha S. Characteristics of a hybrid transducer-type ultrasonic motor[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 1991, 38(3): 188-193.
[6]孙合明, 郭辉. 纵扭复合型超声电机预压力和输出扭矩的关系[J]. 摩擦学学报, 2001, 21(1): 51-54.
SUN He-min, GUO Hui. The relation of pre-pressure and output-torque of longitudinal and torsional ultrasonic motor[J]. Tribology, 2001, 21(1): 51-54.
[7]Satonobu J, Friend J, Nakamura K, et al. Numerical analysis of the symmetric hybrid transducer ultrasonic motor[J]. IEEE Transactions on Ultrasonics, Ferro-electrics and Frequency Control, 2001, 48(6): 1625-1631.
[8]Kurosawa M, Ueha S. Hybrid transducer type ultrasonic motor[J]. IEEE Transactions on Ultrasonics, Ferro-electrics and Frequency Control, 1991,38(3): 89-92.
[9]Tomikawa K, Adachi M, Aoyagi T, et al. Some constructions and characteristics of rod type piezoelectric ultrasonic motors using longitudinal and torsional vibrations[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 1992, 39(5): 600-608.
[10]Aoyagi M, Tomikawa Y. Improvement in performance of longitudinal and torsional vibrator combination-type ultrasonic motor[J]. Jpn J Appl Phys, 1999, 38(5B): 3342-3346.
[11]Takahashi S. Multilayer piezoelectric ceramic actuators and their applications[J]. Jpn J Appl Phys, 1985, 24(2): 41-45.
[12]林书玉.夹心式压电超声扭转换能器的设计[J].压电与声光,1994,16(1):24-28.
LIN Shu-yu. Design of piezoelectric ceramic ultrasonic trosional sandwich transducers[J]. Piezoelectrics & Acoustooptics, 1994,16(1):24-28.
[13]郭海训,魏燕定,郭吉丰,等.纵扭复合型超声波电机压电振子的设计[J].压电与声光,2000,22(5):341-344.
GUO Hai-xun, WEI Yan-ding, GUO Ji-feng, et al. The devign of the piezoelectric vibrator of the congitudinal-torsional composite USM[J]. Piezoelectrics & Acoustooptics, 2000, 22(5): 341-344.
[14]Aoyagi M, Tsuchiya S, Murasawa Y. Trial production of an ultrasonic motor using longitudinal and torsional vibrations of a rod vibrator driven by piezo-ceramic plates inserted in its axial direction[J]. Jpn J Appl Phys, 1997, 36(9B): 6106-6109.
[15]袁世明, 姜开利, 曲建俊,等. 基于扭纵复合型超声电机动力学模型的模拟计算[J]. 压电与声光, 2002, 24(4): 318-322.
YUAN Shi-ming, JIANG Kai-li, QU Jian-jun, et al. A dynamic model of longitudinal and torsional hybrid type ultrasonic motor[J]. Piezoelectrics and Acoustooptics, 2002, 24(2): 318-322.
[16]徐旭, 梁艳春, 时小虎. 纵扭振动超声马达的力学模型[J]. 声学学报, 2003, 28(3): 223-228.
XU Xu, LIANG Yan-chun, SHI Xiao-hu. Mechanical modeling of a longitudinally vibration ultrasonic motor[J]. Acta Acustica, 2003, 28(3):223-228.
[17]Aoyagi M, Tomikawa Y, Takano T. Simplified equivalent circuit of an ultrasonic motor and its applications[J]. Ultrasonics, 1996, 34(4): 275-278.
[18]LIN Shu-yu. Study on the sandwiched piezoelectric ultrasonic torsional transducer[J]. Ultrasonics, 1994, 32(6): 461-464.

收稿日期:2005 -03 -28

基金项目:国家自然科学基金重大项目(50390064); 国家“973”计划项目(2003CB716202)

作者简介:易幼平(1966-), 男, 湖南湘潭人, 博士, 副研究员, 从事超声换能器与微电子封装等研究

论文联系人: 易幼平, 男, 博士; 电话: 0731-8836499(O); E-mail: yyp@mail.csu.edu.cn