Disturbance rejection control for Raymond mill grinding system based on disturbance observer
来源期刊:中南大学学报(英文版)2017年第9期
论文作者:陈夕松 牛丹 杨俊 周杏鹏
文章页码:2019 - 2027
Key words:disturbance observer; proportional integral-disturbance observer (PI-DOB); disturbance rejection; Raymond mill; grinding process
Abstract: In the Raymond mill grinding processes, high-accuracy control for the current of Raymond mill is vital to enhance the product quality and production efficiency as well as cut down the consumption of spare parts. However, strong external disturbances, such as variations of ore hardness and ore size, always exist. It is not easy to make the current of Raymond mill constant due to these strong disturbances. Several control strategies have been proposed to control the grinding processes. However, most of them (such as PID and MPC) reject disturbances merely through feedback regulation and do not deal with the disturbances directly, which may lead to poor control performance when strong disturbances occur. To improve disturbance rejection performance, a control scheme based on PI and disturbance observer is proposed in this work. The scheme combines a feedforward compensation part based on disturbance observer and a feedback regulation part using PI. The test results illustrate that the proposed method can obtain remarkable superiority in disturbance rejection compared with PI method in the Raymond mill grinding processes.
Cite this article as: NIU Dan, CHEN Xi-song, YANG Jun, ZHOU Xing-peng. Disturbance rejection control for Raymond mill grinding system based on disturbance observer [J]. Journal of Central South University, 2017, 24(9): 2019–2027. DOI:https://doi.org/10.1007/s11771-017-3611-9.
J. Cent. South Univ. (2017) 24: 2019-2027
DOI: https://doi.org/10.1007/s11771-017-3611-9
NIU Dan(牛丹), CHEN Xi-song(陈夕松), YANG Jun(杨俊), ZHOU Xing-peng(周杏鹏)
Key Laboratory of Measurement and Control of Complex Systems of Engineering of Ministry of Education,School of Automation, Southeast University, Nanjing 210096, China
 Central South University Press and Springer-Verlag GmbH Germany 2017
Central South University Press and Springer-Verlag GmbH Germany 2017
Abstract: In the Raymond mill grinding processes, high-accuracy control for the current of Raymond mill is vital to enhance the product quality and production efficiency as well as cut down the consumption of spare parts. However, strong external disturbances, such as variations of ore hardness and ore size, always exist. It is not easy to make the current of Raymond mill constant due to these strong disturbances. Several control strategies have been proposed to control the grinding processes. However, most of them (such as PID and MPC) reject disturbances merely through feedback regulation and do not deal with the disturbances directly, which may lead to poor control performance when strong disturbances occur. To improve disturbance rejection performance, a control scheme based on PI and disturbance observer is proposed in this work. The scheme combines a feedforward compensation part based on disturbance observer and a feedback regulation part using PI. The test results illustrate that the proposed method can obtain remarkable superiority in disturbance rejection compared with PI method in the Raymond mill grinding processes.
Key words: disturbance observer; proportional integral-disturbance observer (PI-DOB); disturbance rejection; Raymond mill; grinding process
1 Introduction
The Raymond mill grinding processes are very important and wildly used in fine powder production industry, for example, in the production of silicon carbide powder, which is broadly employed in the field of cutting the silicon slices [1, 2]. Grinding process holds almost 50% of the total expenditure of concentrator plant. It grinds to obtain fine powder products with special size ranges. Effective control for the grinding process is vital to improve the product quality, market competition and cut down energy consumption. In general, the key goals of Raymond mill grinding process are to ensure the stability of the powder product size and effective control of operating load. These require the precise and stable control for the feed rate of fresh ores [1, 2]. The ore hardness and ore size always vary and these variations are hard to express with an accurate mathematical model [3, 4]. In this case, undesirable characteristics, such as time delays and strong disturbances, exist when controlling the operating load (represented by the current of Raymond mill). It is a challenge to control the grinding process with constant current of Raymond mill under the condition of changeable and usually unpredictable ore hardness and ore size. In order to address this issue, a widely used method in Raymond mill grinding process is to use a programmable logic controller (PLC), electromagnetic vibration feeder and current sensor to form a PID-based feedback control loop [5]. The current of Raymond mill can be stabilized by regulating the feed rate of fresh ores using the electromagnetic vibration feeder. However, the system performance with the widely-used PID controller, such as peak overshoot and settling time, is not so satisfied in the case of large ore hardness and feed ore size variation disturbances. To overcome this problem, some more advanced control algorithms are proposed, including intelligent expert control [6], fuzzy logic algorithm [7-9], neural network [10, 11], model-predictive control [12, 13], optimal control [14, 15], and so on. Note that, complexity of tuning and maintenance sometimes lower the attractiveness of the advanced methods comparing with the well-known and industrially-proven PID algorithm controller.
In the Raymond mill grinding process, various disturbances, including external ones and internal ones, exist in constant current of Raymond mill control system. External disturbances, such as the large variations of ore hardness, ore size and the nonlinear characteristics of electromagnetic vibration feeder, will influence the current of Raymond mill. At the same time, internal disturbances, generally caused by model mismatch, may cause poor dynamic performance and even unstable result in the closed-loop system. Note that, the mentioned advanced control principles can only reject disturbances by the feedback regulation, which means that they do not solve the disturbances directly by controller design.
Considering that some disturbances are impossible to measure or forecast, a feedforward compensation based on disturbance observer (DOB) is introduced for improving the performance of constant current of Raymond mill control system. DOB is an effective technique to estimate disturbances and widely applied for feedforward compensation [16-19]. A simple form of DOB was proposed in Ref. [16], which does not need to solve the plant model inverse. In Ref. [17], a generalized DOB capable of estimating higher order disturbances in the time series expansion is described. Moreover, a second-order disturbance observer was used for nonlinear position tracking controller in Ref. [19].
In this work, based on a Raymond mill grinding system in a silicon carbide powder product factory, a DOB-PID scheme is proposed to improve the disturbance rejection performance of the grinding process. The scheme combines a feedforward compensation part based on DOB and a feedback regulation part using PID. It inherits the advantages of both PID and DOB.
2 Process description
Silicon carbide powder has great hardness and is widely used in the field of cutting the silicon slices. In the production of the silicon carbide powder, crushing, grinding, purification and hydraulic overflow classification are important and necessary processes. The raw ores, generally too large, are crushed into the fresh ore with appropriate size for grinding process. In the grinding process, the crushed silicon carbide ores are grinding into the silicon carbide powders with special size range (e.g. 9.5-11.5 μm). Then, these powders can be further classified into the different powder products by the hydraulic classification process. The key goals of Raymond mill grinding process are to maintain stable and effective control for the product powder size and the operating load. They are very important for improving the product quality and cutting down the consumption of spare parts.
A typical simplified Raymond mill grinding process is shown in Fig. 1. It is obvious that the system consists of a vibration feeder, Raymond mill, air classifier, air blower, storage tank, PLC controller and current sensor. The PLC controller gathers real-time current of Raymond mill by the current sensor and produces the control signal to vibration feeder, which is used to regulate the feed rate of carbide silicon ores.

Fig. 1 Schematic diagram of a Raymond mill grinding process
In the Raymond mill grinding process, the raw silicon carbide ores are first fed into the tank of the ground mill by the vibration feeder and then are grinded into the silicon carbide powders using the grinding rollers and grinding rings. The air blower supplies the wind into the tank of the Raymond mill and then the silicon carbide powders are blown into the air classfier for classification. The silicon carbide powders with special size ranges will pass through the air classifier and are collected into the storage tanks; otherwise, the silicon carbide powders with other sizes will drop back into the tank of the Raymond mill for regrinding. Note that in this process, the operating load should be kept at a desired set-point by regulating the feed rate of silicon carbide ores. Too large operating load increases the possibility of production accidents and also affects the uniformity of the powder product sizes. On the contrary, too small operating load will reduce the yields and the production efficiency. In addition, strong external disturbances, such as variations of ore hardness and ore size, always exist. Thus, keeping a constant operating load is an important and difficult task in this grinding system.
In the Raymond mill grinding process, the operating load, represented by the current of Raymond mill y (A), is the most important controlled variable, which needs to be kept at a desired set-point. Larger or smaller operating load than the set-point will degrade the efficiency of the whole grinding process. The current sensor measures and displays the real-time current of Raymond mill and then transmits to PLC controller. Moreover, the silicon carbide powders are our desired product and the powder product size y2 (e.g. 800 mesh) is another important controlled variable. However, usually frequency converters, set by the PLC controller, are designed to regulate the air speed of air blower and the rotate speed of air classifier according to the requirement of powder product size. Thus, only one controlled variable, the current of Raymond mill y (A) is considered. Note that, strong external disturbances including the variations of ore hardness h and feed ore size ds, will cause the continuous fluctuations of the current of Raymond mill. The feed rate of silicon carbide ore x (100 kg/h), controlled by the PLC controller, is the manipulated variable. The PLC controller controls the supply voltage of the electromagnetic vibration feeder and further regulates the feed rate using the silicon controlled rectifier.
3 Control scheme based on PID and disturbance observer
In this section, a composite control scheme is proposed to control the current of Raymond mill in the Raymond mill grinding process. It enhances the performance of the classical PID feedback controller by adding a disturbance observer, which reconstructs and rejects the unwanted perturbation, including the modelling mismatches and the external disturbances. To begin with, DOB technique is introduced. A DOB-PID control scheme is then illustrated in details.
The Raymond mill grinding process is a typical and commonly used industry process. In this process, the operating load (represented by the current of Raymond mill) can be regulated by controlling the feed rate of raw ores [7, 13]. This dynamics can be modeled as a first-order plus dead-time (FOPDT) form [5, 12, 20], which is most commonly used model to describe the dynamics of industrial process [5]. The time delay is unavoidable due to ore transport delay through vibration feeder and measurement sample delay. The transfer function can be represented as
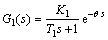 (1)
(1)
where K1 is the transfer factor from feed rate to the current of Raymond mill; T1 is the time constant; θ is the time delay.
Moreover, the bandwidth of the current sensor can satisfy the requirements of this system, so the transfer function of the current sensor can be approximated by a proportional cycle K2.
In summary, the total transfer function of the constant current of Raymond mill in the Raymond mill grinding process can be represented as
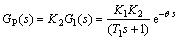 (2)
(2)
3.1 Disturbance rejection control algorithm
In the Raymond mill grinding process, the constant current of Raymond mill control system can be modeled as a first-order plus dead-time (FODT) process. The system can be considered using the following model:
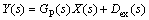 (3)
(3)
where
 (4)
(4)
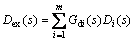 (5)
(5)
In Eqs. (3)-(5), X(s) is the manipulated variable;Y(s) is the controlled variable; Dex(s) is the effect of external disturbances on Y(s); Di(s) (i=1, 2, …, m) are the ith external disturbances; GP(s) is the model of the process channel; g(s) is the minimum-phase part of GP(s); Gdi(s) (i=1, 2, …, m) is the model of the ith disturbance channel. The nominal model Gn(s) can also be represented as a product of a minimum-phase part gn(s) and a dead-time part 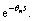
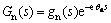 (6)
(6)
3.2 Disturbance observer-enhanced PID algorithm
In this work, a composite control scheme is proposed to enhance the performance of the classical PID feedback controller by adding a disturbance observer. Considering that the nominal model Gn(s) includes a time-delay part 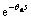 and the inverse of time delay part cannot be physically realized, a modified DOB based PID control scheme is developed for the Raymond mill grinding system. The block diagram is presented in Fig. 2.
and the inverse of time delay part cannot be physically realized, a modified DOB based PID control scheme is developed for the Raymond mill grinding system. The block diagram is presented in Fig. 2.
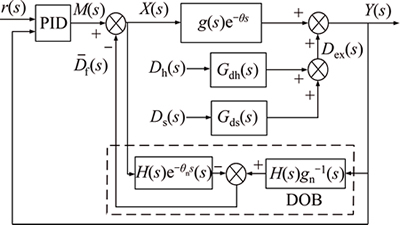
Fig. 2 Block diagram of disturbance observer-enhanced PID control
In this figure, r(s) denotes the reference trajectory of controlled variable. M(s) represents the output of the PID controller. 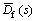 is the disturbance estimation. The output can be represented as
is the disturbance estimation. The output can be represented as
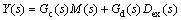 (7)
(7)
with
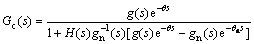 (8)
(8)
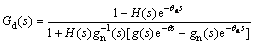 (9)
(9)
From Eqs. (7)-(9), we can obtain that the performance of disturbance rejection mainly depends on the design of filter H(s). It can be found that 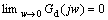 when H(s) is selected as a low-pass filter with a steady-state gain of 1, i.e.,
when H(s) is selected as a low-pass filter with a steady-state gain of 1, i.e., 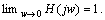 It means that low frequency disturbances can be attenuated asymptotically. In this work, H(s) is selected as a first-order low-pass filter with a steady-state gain of 1, which can be represented as
It means that low frequency disturbances can be attenuated asymptotically. In this work, H(s) is selected as a first-order low-pass filter with a steady-state gain of 1, which can be represented as
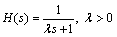 (10)
(10)
As for the robustness of the proposed DOB, it will be analyzed as follows. From Fig. 2, the output Y(s) can be represented as
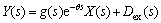
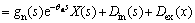 (11)
(11)
where the term Din(s) is the internal disturbances caused by model mismatches and it can be denoted as
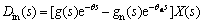 (12)
(12)
Now, define the lumped disturbance Dp(s) as the sum of external disturbances Dex(s) and internal as disturbances Din(s), that is,
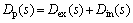 (13)
(13)
Then the output can be obtained as
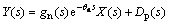 (14)
(14)
Moreover, from Fig. 2, the following equations can be obtained as
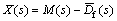 (15)
(15)
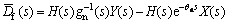 (16)
(16)
Substituting Eq. (14) into Eq. (16), we can obtain
 (17)
(17)
Define 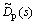 as the error between the real value and the estimation value of lumped disturbance, then
as the error between the real value and the estimation value of lumped disturbance, then
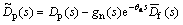 (18)
(18)
Substituting Eq. (17) into Eq. (18) yields
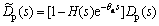 (19)
(19)
Employing the final-value theorem, the following equation can be obtained as
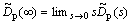
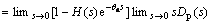
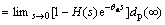 (20)
(20)
Therefore, if satisfying that the steady-state gain of H(s) is 1, then 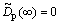 can be obtained. It means that the disturbances can be asymptotically rejected. Note that, the implementation of DOB is quite simple and the computational complexity will not be increased largely for the introduction of feed-forward compensation. Thus, the modified disturbance observer is a practical approach to deal with the process with time delay.
can be obtained. It means that the disturbances can be asymptotically rejected. Note that, the implementation of DOB is quite simple and the computational complexity will not be increased largely for the introduction of feed-forward compensation. Thus, the modified disturbance observer is a practical approach to deal with the process with time delay.
3.3 Control implementation
In this work, the proposed control scheme focuses on disturbance rejection against external disturbances as well as model mismatches. The controlled variable is the current of Raymond mill y(A), while the manipulated variable is the feed rate of silicon carbide ores x (100 kg/h). The variations of ore hardness dh and feed ore size ds are the main external disturbance variables. The detailed control structure is shown in Fig. 3.
DOB-based PID strategy is programmed by the configuration software IFIX from intellution on a supervisory computer. Final commands are carried out through the PLC, while the real-time current signal of Raymond mill from current sensor is also connected and sampled to the PLC controller.
From Fig. 3, it can be obtained that the ore hardness and size disturbances directly affect the primary output (the current of Raymond mill). For control study, plant test has been constructed to develop the transfer function model as follows [5]:
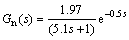 (21)
(21)
The nominal values of Raymond mill grinding system are: the current of Raymond mill, 60 A. The external disturbances are imposed on the process through disturbance channels. It is known that the ore hardness and feed ore size have great influence on the current of Raymond mill. For example, ore feed with increased ore hardness or increased ore size leads to a increased current of Raymond mill, and the dynamics can be also modeled as a first-order plus dead-time (FOPDT) form, which is the most commonly used model to describe the dynamics of industrial process [5, 12]. For simulation study, the transfer functions of disturbance channels Gdh(s) and Gds(s) can be obtained by mechanism analysis of process and expressed as follows:
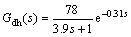 (22)
(22)
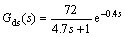 (23)
(23)
The time constants are expressed in seconds here.Gdh(s) and Gds(s) denote the transfer functions of disturbance channels ore hardness variations and feed ore size variations, respectively. Note that, both ore hardness and feed ore size are hard or impossible to be measured. Thus, here they are expressed in a relative change form rather than a real physical unit form. For example, dh=10% means that the ore hardness has an increase of 10% compared with its nominal value.
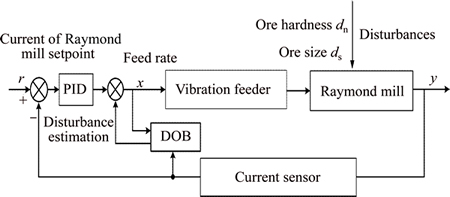
Fig. 3 Control structure of constant current of Raymond mill via proposed method
Moreover, based on the above discussions, the filter of DOB is employed as
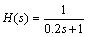 (24)
(24)
The PID controller parameters are determined by Z-N algorithm combined with trial and error. They are designed as
Kp=0.86, KI=0.18 (25)
4 Performance analysis and comparisons
In this part, some results are shown to demonstrate the benefits and practicality of the proposed method. The baseline PI controller is employed for the comparison and the disturbance rejection performance is studied in the nominal case as well as the model mismatch case.
4.1 Disturbance rejection in nominal case
Firstly, the nominal case is considered for studying the disturbance rejection performance of grinding process under the proposed method. It means that the transfer function model of process channel GP(s) satisfies the Gn(s)=GP(s). In the Raymond mill grinding system, external disturbances including the ore hardness and feed ore size usually fluctuate arbitrarily, but continuously, slowly and with the limited magnitudes during the whole production [21], thus a sinusoidal disturbance is likely to match the features of the real practice better than a common step disturbance. Therefore, besides the step disturbance case, a sinusoidal disturbance case is also considered and simulated.
Case I: Step external disturbances in the nominal case. The ore hardness has an increase of 10% at t=20 s, while the feed ore size has a decrease of 20% at t=50 s.
Figure 4(a) shows the response curves of the current of Raymond mill under the control of both DOB-PI and PI in the case I. The corresponding changes of manipulated variables are presented in Fig. 4(b).Figure 4(c) gives the effects of external disturbances and the estimations on the controlled variables. From Fig. 4(a), it is clear that the dynamic performance of the current of Raymond mill under the proposed method is much better than those under the PI method. Compared with the conventional PI method, the proposed method can obtain a faster convergence speed, smaller amplitudes of fluctuations and shorter settling times. From Fig. 4(c), it can be observed that the errors between the estimated and real external disturbances are very small, which means that the disturbance observer can effectively estimate the effects caused by disturbances.
In order to quantitatively analyze the disturbance rejection performance, two performance indexes including peak overshoot and integral of absolute error (IAE) are employed as shown in Table 1. From Table 1, it is clear that both the overshoot and the IAE value of the current of Raymond mill are much smaller than those under the PI method.
Case II: Sinusoidal external disturbances in the nominal case. Variations of the ore hardness and ore size are sinusoidal, i.e., d =Asin(wt), ds=Bsin(wt), here A=10%, B=20%, w=0.2 rad/s.
Figure 5(a) shows the response curves of current of Raymond mill under the control of both DOB-PI and PI in the case II. The corresponding changes of manipulated variables are presented in Fig. 5(b). Figure 5(c) gives the effects of real disturbances and the estimations by the disturbance observer. From Fig. 5(a), the fluctuation amplitude of the current of Raymond mill under the proposed method is much smaller than that under the conventional PI method, although the fluctuation frequencies of the controlled variable under the two methods are almost the same. It can be seen from Fig. 5(b) that the fluctuation frequency and amplitude of the manipulated variable under the proposed method are almost the same with those under the PI method. However, the variation of the manipulated variable under the proposed method is a little faster than that under the PI method. Moreover, from Fig. 5(c), the real and the estimated disturbances almost overlap. Therefore, the proposed method is more effective to overcome such sinusoidal external disturbance than the conventional PI method.
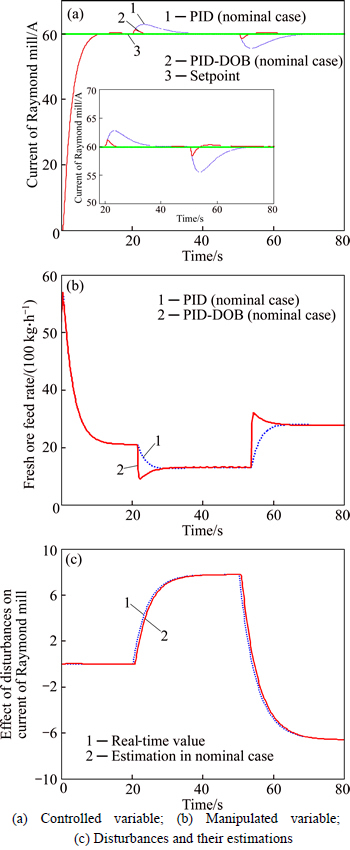
Fig. 4 Response curves of variables in the presence of step external disturbances under DOB-PI and PI schemes in nominal case:
Table 1 Performance indexes in the presence of step external disturbances for nominal case


Fig. 5 Response curves of variables in the presence of sinusoidal external disturbances under DOB-PI and PI schemes in nominal case:
4.2 Disturbance rejection in model mismatch case
In real practice, besides external disturbances, internal disturbances caused by model mismatches are other important factors which affect the control performance of the closed-loop system. As illustrated in section 3, the proposed method can reject not only external disturbances, but also the internal disturbances caused by model mismatches. In this part, some simulation studies are done to demonstrate the lumped disturbance rejection performance of the proposed method.
Suppose that the transfer function model of process channel is expressed as
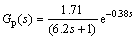 (26)
(26)
Comparing Eq. (26) with Eq. (21), it is clear that severe model mismatch exists.
Case III: Step external disturbances in the model mismatch case. The ore hardness has an increase of 10% at t=20 s, while the feed ore size has a decrease of 20% at t=50 s.
Figure 6(a) shows the response curves of the current of Raymond mill under the control of the two methods. The corresponding responding curves of manipulated variables are presented in Fig. 6(b). Figure 6(c) gives the effects of lumped disturbances and the estimations in this case. The performance indexes are listed in Table 2.
Similar with Case I, it can be observed from Fig. 6(a) and Table 2 that the proposed method possesses a smaller peak overshoot, a smaller values of IAE and a faster convergence speed, etc. This means that the proposed method has achieved a much better step disturbance rejection performance than the PI method even in the case of severe model mismatches. Moreover, the errors between the estimated and the real lumped disturbances are also very small.
Case IV: Sinusoidal external disturbances in the model mismatch case. Variation of ore hardness is sinusoidal, i.e., dh=Asin(wt), ds=Bsin(wt), here A=10%, B=20%, w=0.2 rad/s.
In Case IV, the response curves of the current of Raymond mill under the control of the proposed method and the PI method are shown in Fig. 7(a). The corresponding changes of manipulated variables are presented in Fig. 7(b). Figure 7(c) gives the effects of estimated lumped disturbances in such case. It can be seen from Fig. 7(a) that the fluctuation amplitudes of the current of Raymond mill under the control of the proposed method (DOB-PI) are much smaller than those under the PI method. The fluctuation frequencies between the two methods are almost the same. From Fig. 7(b), the fluctuation amplitudes of the manipulated variable under the proposed method are a little larger than those under the PI method, but the change is quicker than that under the PI method. Moreover, the disturbance estimation errors in this case are also small from Fig. 7(c). Those simulation results demonstrate that the proposed method has remarkable superiorities in rejecting such lumped disturbances consisting of sinusoidal external disturbances and internal disturbances caused by model mismatches.
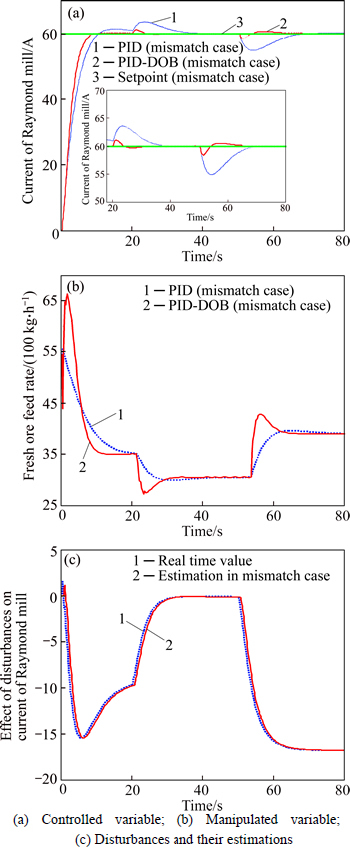
Fig. 6 Response curves of variables in presence of step external disturbances under DOB-PI and PI schemes in mismatch case:
Table 2 Performance indexes in presence of step external disturbances for model mismatch case

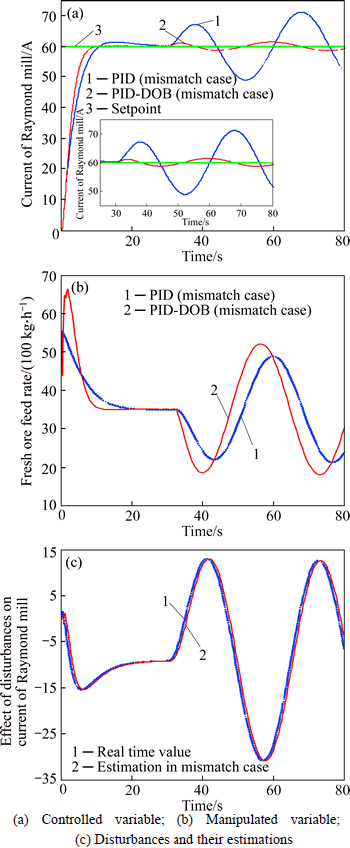
Fig. 7 Response curves of variables in the presence of sinusoidal external disturbances under DOB-PI and PI schemes in mismatch case:
5 Conclusions
In the Raymond mill grinding process, various complex and immeasurable disturbances have undesirable influences on constant current of Raymond mill control system. Many existing methods in industrial process control including PID have limitations in handling strong disturbances. In order to improve the disturbance rejection performance, disturbance observer has been introduced for feedforward compensation in this work. A composite control scheme combining a feedforward compensation part based on DOB with a feedback regulation part based on PID has been developed. Both external disturbances and internal disturbances caused by model mismatches are taken into consideration. Disturbances rejection property is then analyzed by simulation and the results have demonstrated that, compared with conventional PID method, the proposed method has exhibited excellent disturbance rejection performance, such as a smaller overshoot and a shorter settling time.
References
[1] SUN Hao, ZHOU Xing-peng. An automatic control system for Raymond milling [J]. Instrumentation Analysis Monitorning, 2008(1): 1-3. (in Chinese)
[2] LV Kuang-sheng, ZHOU Xing-peng, TAO Lian-bin, NIU Dan. Design and realization of Raymond mill control system based on fuzzy PID [J]. Process Automation Instrumentation, 2009, 30(2): 27-30. (in Chinese)
[3] CRAIG I K. Grindingmillmodeling and control: past, present and future [C]// 31st Chinese Control Conference. Hefei, China: IEEE, 2012: 16-21.
[4] LU Shao-wen,ZHOU Ping,CHAI Tian-you, DAIWei. Modeling and simulation of whole ball mill grinding plant for intergrated control [J]. IEEE Transactions on Automation Science and Engineering, 2014, 11(4): 1004-1019.
[5] POMERLEAU A, HODOUIN D, DESBIENS A, GAGNON E. A survey of grinding circuit control methods: From decentralized PID controllers to multivariable predictive controllers [J]. Powder Technol, 2000, 108(2, 3): 103-115.
[6] BHAUMIK A, SIL J,MAITY S,DAS T S. Designing an intelligent expert control system using acoustic signature for grinding mill operation [C]// IEEE International Conference on Industrial Technology. Mumbai, India: IEEE, 2006: 500-505.
[7] TANG Yao-geng, SONG Gao. The mill load control for grinding plant based on fuzzy logic [C]// IEEE International Conference on Machine Learning and Cybernetics. Beijing, China: IEEE, 2002, 1: 416-419.
[8] WU Xing-gang,YUAN Ming-zhe, YU Hai-bin. Product flow rate control in ballmillgrindingprocess using fuzzy logic controller [C]// IEEE International Conference on Machine Learning and Cybernetics. Hebei, China: IEEE, 2009, 2: 761-764.
[9] ZHAO Da-yong, CHAI Tian-you, WANG Hong, FU Jun. Hybrid intelligent control for regrinding process in hematite beneficiation [J]. Control Eng Practice, 2014, 22: 217-223.
[10] CONRADLE A V E, ALDRICH C. Neuro control of a ball mill grinding circuit using evolutionary reinforcement learning [J]. Minerals Engineering, 2001, 14: 1277-1294.
[11] GOVINDHASAMY J J, MCLOONE S F, IRWIN G W, FRENCH J J, DOYLE R P. Neural modelling, control and optimization of an industrial grinding process [J]. Control Engineering Practice, 2005, 13(10): 1243-1258.
[12] CHENG Xi-song, LI Qi, FEI Shui-min. Constrained model predictive control in ball mill grinding process [J]. Powder Technology, 2008, 186(1): 31-39.
[13] COETZEE L C, CRAIG I K, KERRIGAN E C. Robust nonlinear model predictive control of a run-of-mine ore milling circuit [J]. IEEE Trans Control Syst Technol, 2010, 18(1): 222-229.
[14] NIETO C H. Testing a predictive controlwith stochastic model in a ballsmillgrindingcircuit [C]// IEEE/IAS International Conference on Industry Applications. Juiz de For a, Brazil: IEEE, 2014: 1-5.
[15] DAI Wei, CHAI Tian-you, YANG S X. Data-driven optimization control for safety operation of hematite grinding process [J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 2930-2941.
[16] DU C, LI H, THUM C K, LEWIS F L, WANG Y. Simple disturbance observer for disturbance compensation [J]. IET Control Theory Appl, 2010, 4(9): 1748-1755.
[17] KIM K S, REW K H, KIM S. Disturbance observer for estimating higher order disturbances in time series expansion [J]. IEEE Transactions on Automatic Control, 2010, 55(8): 1905-1911.
[18] GUO Kai,WEI Jian-hua,TIAN Qi-yan. Disturbance observer based position tracking of electro-hydraulic actuator [J]. Journal of Central South University, 2015, 22(6): 2158-2165.
[19] JIN Qi-bing, LIU Li-ye. Design of activedisturbancerejection internal model control strategy for SISO system with time delay process [J]. Journal of Central South University, 2015, 22(5): 1725-1736.
[20] DESBIENS A, NAJIM K, POMERLEAU A, HODOUIN D. Distributed partial state reference model adaptive control — practical aspects and application to a grinding circuit [J]. Optimal Control Applications and Methods, 1997, 18: 29-47.
[21] DUAN Xi-xiang. Crushing and Grinding [M]. Beijing: Metallurgical Industry Press, 2010. (in Chinese)
(Edited by YANG Hua)
Cite this article as: NIU Dan, CHEN Xi-song, YANG Jun, ZHOU Xing-peng. Disturbance rejection control for Raymond mill grinding system based on disturbance observer [J]. Journal of Central South University, 2017, 24(9): 2019–2027. DOI:https://doi.org/10.1007/s11771-017-3611-9.
Foundation item: Projects(61504027, 61573099) supported by the National Natural Science Foundation of China; Project(BK20140647) supported by the Natural Science Foundation of Jiangsu Province, China; Project supported by the Priority Academic Program Development of Jiangsu Higher Education Institutions, China
Received date: 2016-02-22; Accepted date: 2016-07-11
Corresponding author: CHEN Xi-song, Professor; Tel: +86-13851562738; E-mail: chenxisong@263.net

