基于三角模糊数的仿真模型验证方法
焦松,李伟,杨明
(哈尔滨工业大学 控制与仿真中心,黑龙江 哈尔滨,150080)
摘要:为了保证仿真模型可信度量化结果的准确性,同时便于验证方法的实际应用,既需要充分考虑各种专家意见带来的不确定性,且需要采用统一的形式对专家意见进行刻画。由此提出基于三角模糊数的验证方法。首先分析专家意见的特点,并采用三角模糊数进行描述;然后将仿真输出分为静态、缓变和速变三类数据,并分别采用相应的图形将各自特征直观地呈现给专家,进而评定得到每个仿真输出分量的符合度;再者基于三角模糊数层次分析法得到各仿真输出变量的权重;最后基于模糊综合评判法综合各仿真输出分量的符合度,得到仿真模型的可信度。在实例应用中,该方法有效地对某导弹导引系统仿真模型进行验证。
关键词:仿真模型验证;三角模糊数;模糊层次分析法;模糊综合评判法
中图分类号:TP391.9 文献标志码:A 文章编号:1672-7207(2014)01-0124-08
Validation method of simulation model based on triangular fuzzy number
JIAO Song, LI Wei, YANG Ming
(Control and Simulation Center, Harbin Institute of Technology, Harbin 150080, China)
Abstract: To ensure the accuracy of the credibility of simulation model and make the validation method convenient for application, the uncertainty of expert opinions needs to be adequately concerned and the expert opinions need to be depicted by the unified form. The validation method of simulation model based on triangular fuzzy number was proposed. Firstly, the feature of expert opinion was analyzed and the expert opinion was depicted by the triangular fuzzy number. Then the simulation output was divided into three kinds: static data, gradual data and fast data. Their features are shown in the corresponding graph. The consistency degree of each kind of data was given by experts via observing data features in the graph, and the weight of each simulation output was obtained based on fuzzy analytic hierarchy process. Lastly, the credibility of simulation model was obtained via integrating the consistency of simulation outputs based on fuzzy comprehensive evaluation. In the application, the simulation model of the guidance system of a missile was validated effectively by the method.
Key words: validation of simulation model; triangular fuzzy number; fuzzy analytic hierarchy process; fuzzy comprehensive evaluation
由于仿真技术的安全性、经济性,且能模拟尚处于设计阶段的系统,使其在国防、经济及化工等众多领域得到了广泛应用[1-2]。仿真是基于模型的活动,由此仿真模型的可信性越来越受到模型用户的关注。仿真模型验证则是确保仿真模型可信的重要工作之一,对于仿真活动具有重要的意义[3]。比较分析仿真输出和参考输出是仿真模型验证的重要手段之一。经典的方法可以分为定性方法、定量方法以定性定量相结合的方法三类:定性方法有表面验证法、动画法、曲线对比法以及图灵测试法等[4-5];定量方法有假设检验法、参数估计法、TIC法、灰色关联法、误差分析法以及频域分析方法等[6-12];定性定量相结合的方法有基于模糊集及证据理论的验证方法等[13-14]。这些方法中,已有的定性方法只能给出定性结论,而不能得到量化的仿真模型可信度值;已有的定量方法是通过分析仿真输出与参考输出之间的特征差异得到验证结果,其只能判定仿真模型是否可信,也不能给出具体的可信度值;已有的定性定量相结合的方法能得到具体的仿真模型可信度值,但是这些方法一方面未能全面地考虑仿真模型验证过程中的不确定性,不能保证仿真模型可信度量化结果的准确性,另一方面未能采用统一的形式对多种不确定性进行刻画,不利于实际应用。基于此,本文作者提出基于三角模糊数的仿真模型验证方法。首先给出问题的描述和分析,然后采用三角模糊数描述仿真模型验证过程中的专家意见,在此基础上给出各仿真输出分量相对参考输出的符合程度以及相互之间重要程度的比值,最后基于模糊层次分析法确定各输出分量权重,并采用模糊综合评判法综合各仿真输出分量符合度得到仿真模型的可信度。
1 问题描述及分析
用S表示系统,I={i1, i2, …, in}和O={o1, o2, …, om}分别表示系统的输入和输出。用Ss和Sr分别表示仿真系统和参考系统,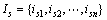 和
和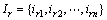 分别表示仿真系统和参考系统的输入,
分别表示仿真系统和参考系统的输入,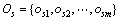 和
和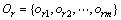 分别表示仿真系统和参考系统的输出。
分别表示仿真系统和参考系统的输出。
用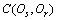 表示在
表示在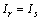 时,Os相对于Or的一致性程度,且
时,Os相对于Or的一致性程度,且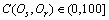 。当Os与Or完全一致,即仿真模型最可信,则有
。当Os与Or完全一致,即仿真模型最可信,则有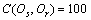 ;当Os相对于Or一致性程度越差,即仿真模型越不可信时,则有
;当Os相对于Or一致性程度越差,即仿真模型越不可信时,则有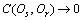 。由此可知:
。由此可知: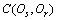 可以视作仿真模型可信度的度量。用
可以视作仿真模型可信度的度量。用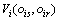 ,i=1, 2, …, m表示在Ir=Is时,ois相对于oir的符合程度,且
,i=1, 2, …, m表示在Ir=Is时,ois相对于oir的符合程度,且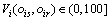 。当ois与oir完全符合时,有
。当ois与oir完全符合时,有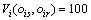 ;当ois与oir符合程度越差时,则有
;当ois与oir符合程度越差时,则有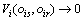 。进一步定义如下:
。进一步定义如下:
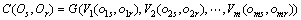 (1)
(1)
式中: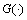 为符合度综合模型。
为符合度综合模型。
式(1)通常采用加权综合的方式实现,由此可进一步定义如下:
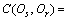
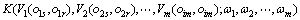 (2)
(2)
其中: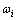 ,i=1, 2, …, m为
,i=1, 2, …, m为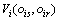 的权重;
的权重;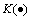 为仿真输出符合度的加权综合模型。
为仿真输出符合度的加权综合模型。
由上分析可知,在多个领域专家的参与下,为了得到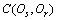 ,存在以下3个难点:
,存在以下3个难点:
(1) 如何组织专家给出不同类型仿真输出的符合度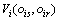 ,i=1, 2, …, m;
,i=1, 2, …, m;
(2) 如何组织专家给出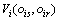 ,i=1, 2, …, m的权重
,i=1, 2, …, m的权重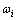 ;
;
(3) 如何对专家的意见进行描述和处理,进而综合得到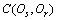 。
。
由于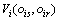 和
和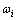 的确定都需要专家的参与,而专家所提供的信息都存在不确定性,因此仿真模型验证的就关键在于如何对
的确定都需要专家的参与,而专家所提供的信息都存在不确定性,因此仿真模型验证的就关键在于如何对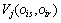 和
和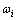 中的不确定性进行刻画和利用。
中的不确定性进行刻画和利用。
2 仿真模型验证中的专家意见描述方法
在仿真模型验证过程中,需要专家给定若干变量的取值。由于专家主观判断的不确定性,很难给出某个变量的准确取值,但是能给出取值的可能区间。在该区间中,变量在其两端取值的可能性较小,而在中间取值的可能性较大。由于专家意见的此种特征,本文采用三角模糊数对其进行刻画。假定论域U为实数集合,U上的全体模糊集合用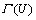 表示,设
表示,设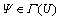 ,若满足[15]:
,若满足[15]:
(1) 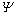 的隶属函数
的隶属函数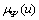 可表示为:
可表示为:
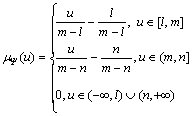 (3)
(3)
(2) 存在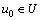 ,使得
,使得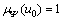 。
。
(3) 对于任意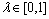 ,
,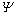 的截集
的截集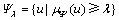 为凸集。
为凸集。
此时,则称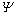 为三角模糊数,可记为(l, m, n)。用n-l表示
为三角模糊数,可记为(l, m, n)。用n-l表示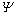 的模糊程度。若n-l越大,则表示
的模糊程度。若n-l越大,则表示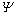 的模糊度越高;若n-l=0,则表示
的模糊度越高;若n-l=0,则表示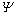 是一确定值,不具有模糊性。
是一确定值,不具有模糊性。
定义2个三角模糊数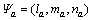 和
和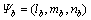 ,其运算方法如下:
,其运算方法如下:
(1) 加法运算: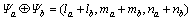 ;
;
(2) 乘法运算: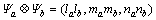 ;
;
(3) 数乘运算: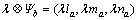 ,其中
,其中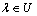 ;
;
(4) 倒数运算: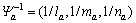 。
。
定义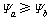 的可能性程度如下:
的可能性程度如下:
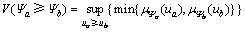 (4)
(4)
如图1所示,依据不同的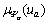 和
和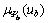 进一步可得:
进一步可得:
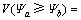
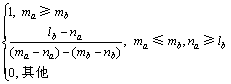 (5)
(5)
进一步,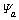 大于其他N个三角模糊数
大于其他N个三角模糊数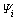 ,i=1, 2, …, N的可能性程度定义如下:
,i=1, 2, …, N的可能性程度定义如下:
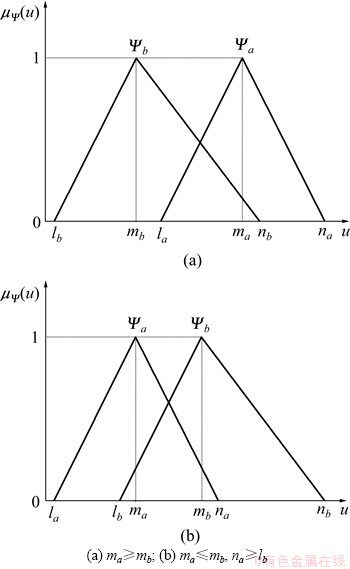
图1 2个三角模糊数关系示意图
Fig. 1 Size relationship of two triangular fuzzy numbers
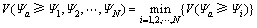 (6)
(6)
3 仿真模型验证中的专家意见处理方法
3.1 仿真输出符合度确定
按数据与时间是否相关进行分类,可以将系统输出分为静态数据和动态数据两类[10]。对于动态数据而言,按数据变化频率的大小进行分类,又可以分为缓变数据和速变数据两类。例如:如图2所示,导弹的脱靶量为静态数据,位姿状态为缓变数据,振动信号为速变数据。
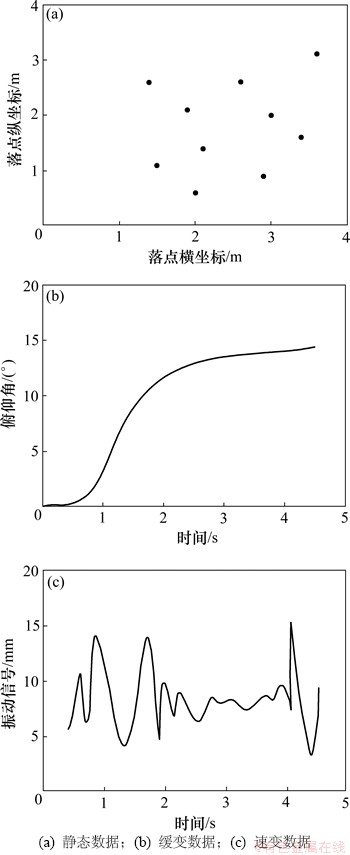
图2 三类数据实例图
Fig. 2 Instances of three kinds of data
仿真输出符合度的确定是邀请专家观察并分析仿真输出和参考输出,进而采用三角模糊数的形式给定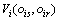 ,i=1, 2, …, m的取值。为了给专家提供更丰富、更直观的数据特征,不同类型的数据则需要根据其所蕴含的特征采用相应的方式进行展现,如表1所示。对于静态数据,需要关注仿真数据和参考数据在集中趋势、离散趋势及分布特征等方面的差异,常以散点图、箱线图或直方图展现。对于缓变数据,需要关注仿真数据和参考数据的位置差异及外形差异。由于其变化频率低,因此可以在时域中直接采用点线图展现。对于速变数据,可以先通过经验模型分解等平稳化处理方法将其分解为趋势项和平稳项,具体算法见文献[16]。其中趋势项为缓变数据,可以在时域中利用点线图展现;由于平稳项时域特征不明显,可将其转换至频域中得到谱密度,并采用Bode图展现。
,i=1, 2, …, m的取值。为了给专家提供更丰富、更直观的数据特征,不同类型的数据则需要根据其所蕴含的特征采用相应的方式进行展现,如表1所示。对于静态数据,需要关注仿真数据和参考数据在集中趋势、离散趋势及分布特征等方面的差异,常以散点图、箱线图或直方图展现。对于缓变数据,需要关注仿真数据和参考数据的位置差异及外形差异。由于其变化频率低,因此可以在时域中直接采用点线图展现。对于速变数据,可以先通过经验模型分解等平稳化处理方法将其分解为趋势项和平稳项,具体算法见文献[16]。其中趋势项为缓变数据,可以在时域中利用点线图展现;由于平稳项时域特征不明显,可将其转换至频域中得到谱密度,并采用Bode图展现。
表1 三类数据的特征及展现方式
Table 1 Features and representation modes of three kinds of data

3.2 仿真输出权重确定
常用的权重确定方法有Delphi法和层次分析法等。其中,层次分析法是一种定性定量相结合的分析方法,能将复杂的决策问题转化为简单的两两比较问题,且易于操作实现,因此应用广泛。进一步考虑到采用三角模糊数描述专家意见,本文基于三角模糊数的层次分析法[17-18]确定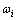 ,i=1, 2, …, m,步骤如下:
,i=1, 2, …, m,步骤如下:
第1步:邀请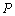 位专家分别给出判断矩阵Ct,t=1, 2, …, P。
位专家分别给出判断矩阵Ct,t=1, 2, …, P。
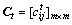 ,t=1, 2, …, P,i, j=1, 2, …, m (7)
,t=1, 2, …, P,i, j=1, 2, …, m (7)
其中: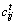 为第t位专家给定的
为第t位专家给定的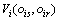 相对
相对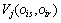 重要程度的倍数,其用三角模糊数来描述。
重要程度的倍数,其用三角模糊数来描述。
第2步:综合P位专家的意见得到判断矩阵C,并进行一致性检验。
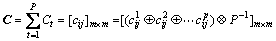 (8)
(8)
第3步:依据判断矩阵C,构造一致性判断矩阵,进行一致性判断。
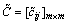 ,
,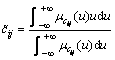 (9)
(9)
其中: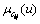 为三角模糊数cij的隶属函数。
为三角模糊数cij的隶属函数。
进一步,得到一致性判断矩阵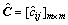 :
:
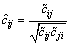 (10)
(10)
计算得到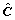 的最大特征向量
的最大特征向量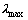 ,进而得到一致性指标如下:
,进而得到一致性指标如下:
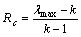 ,
,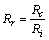 (11)
(11)
其中:Rc为一致性指标;k为数据特征差异个数;Ri为平均随机一致性指标,其取值与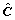 的阶数有关,参见文献[19];Rr为随机一致性比率。
的阶数有关,参见文献[19];Rr为随机一致性比率。
当Rr≤0.10时,即可认为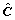 的一致性能被接受,进而间接判定C的一致性能被接受;否则,就需要重新调整判断矩阵C。
的一致性能被接受,进而间接判定C的一致性能被接受;否则,就需要重新调整判断矩阵C。
第4步:若判断矩阵C通过了一致性检验,则可以依据其确定各仿真输出符合度的权重。
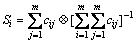 ,
,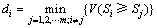 ,
,
i=1, 2, …, m (12)
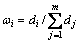 ,i=1, 2, …, m (13)
,i=1, 2, …, m (13)
对于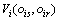 ,i=1, 2, …, m的取值,P位专家给出的基于三角模糊数的评价结果为:
,i=1, 2, …, m的取值,P位专家给出的基于三角模糊数的评价结果为:
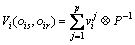 (14)
(14)
其中: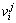 为第j位专家对
为第j位专家对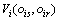 的评价结果。
的评价结果。
3.3 仿真输出符合度综合
确定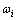 和
和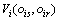 ,i=1, 2, …, m之后,需要进行综合处理得到
,i=1, 2, …, m之后,需要进行综合处理得到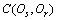 。模糊综合评判法能有效地对带有模糊性的专家意见进行综合,但该方法需要以模糊向量形式刻画指标值。由于
。模糊综合评判法能有效地对带有模糊性的专家意见进行综合,但该方法需要以模糊向量形式刻画指标值。由于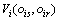 ,i=1, 2, …, m在本文中采用三角模糊数形式刻画。在此,先将三角模糊数转换为模糊向量,然后再利用模糊综合评判法综合
,i=1, 2, …, m在本文中采用三角模糊数形式刻画。在此,先将三角模糊数转换为模糊向量,然后再利用模糊综合评判法综合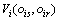 ,i=1, 2, …, m得到
,i=1, 2, …, m得到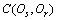 [17-18],步骤如下:
[17-18],步骤如下:
第1步:建立因素集合及权重集。
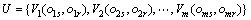 ,
,
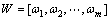 (15)
(15)
其中:U为因素集;W为对应的权重集。
第2步:建立评价集。
评价集定义如下:
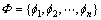 (16)
(16)
评价集中的元素个数,一般反映了人们对事物的区分程度,通常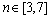 。本节令n=5,进一步具体化评价集为:
。本节令n=5,进一步具体化评价集为:
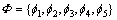 (17)
(17)
其中: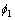 为“很不符合”;
为“很不符合”;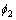 为“不符合”;
为“不符合”;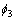 为“一般符合”;
为“一般符合”;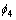 为“很符合”;
为“很符合”;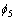 为“十分符合”。
为“十分符合”。
确定评价集中各元素在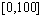 上的隶属函数
上的隶属函数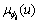 ,i=1, 2, 3, 4, 5。图3所示为三角形的隶属函数。
,i=1, 2, 3, 4, 5。图3所示为三角形的隶属函数。
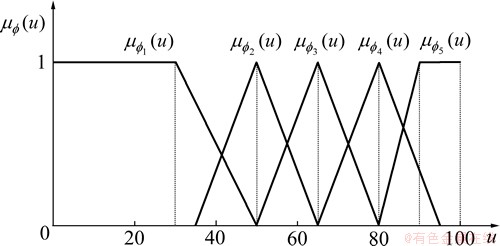
图3 评价集中各元素的隶属函数
Fig. 3 Membership functions of elements in evaluation set
第3步:对单个因素进行模糊评判。
假定P位专家对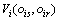 ,i=1, 2, …, m的综合评价结果为:
,i=1, 2, …, m的综合评价结果为:
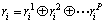 (18)
(18)
其中: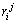 ,j=1, 2, …, P为第j位专家的评价结果。
,j=1, 2, …, P为第j位专家的评价结果。
进一步,将三角模糊数r i,i=1, 2, …, m转化为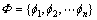 上的模糊集合Ri,i=1, 2, …, m如下:
上的模糊集合Ri,i=1, 2, …, m如下:
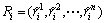 (19)
(19)
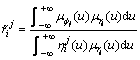 ,j=1, 2, …, n (20)
,j=1, 2, …, n (20)
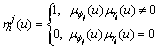 ,
,
i=1, 2, …, m,j=1, 2, …, n (21)
第4步:构造模糊关系矩阵并得到综合评价结果。
依据Ri,i=1, 2, …, m,建立因素集U和评价集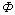 之间的模糊关系矩阵为:
之间的模糊关系矩阵为:
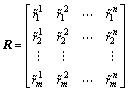 (22)
(22)
其中:R为模糊关系矩阵。
由此,得到综合评价结果为:
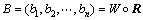 (23)
(23)
其中: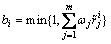 ,i=1, 2, …, n。
,i=1, 2, …, n。
对B进行去模糊化处理[20],得到最终的评价结果如下:
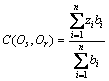 (24)
(24)
其中: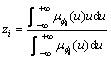 。
。
4 应用实例
假定模型用户需要研究某导弹的比例导引系统,其攻击平面为铅垂面,与目标的相对位置关系如图4所示。其中,M表示导弹;T表示目标;v为导弹速度;vT为目标速度;q为目标线角;η为导弹速度矢量前置角;θ为导弹弹道角,由于攻击平面为铅垂面,所以其也是弹道倾角;ηT为目标速度矢量前置角;σT为目标航向角。依据各物理量之间的关系以及导引关系,建立的系统模型如下所示:
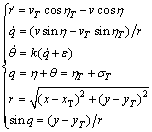 (25)
(25)
式中:r为导弹和目标之间的距离;ε为测量目标线角的噪声信号;x和y分别为导弹位置的横坐标和纵坐标;xT和yT分别为目标位置的横坐标和纵坐标。
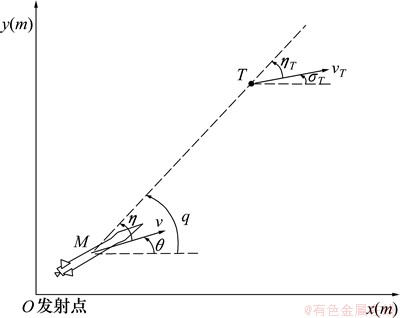
图4 目标与导弹的相对位置
Fig. 4 Relative position of missile and target
对于模型用户而言,其关注的系统输出包含导弹的位姿信息、弹道倾角速度以及脱靶量。在这多个系统输出中,导弹的位姿信息为缓变数据,弹道倾角速度中由于包含了噪声,因此视为速变数据,而脱靶量为静态数据。经典的分析方法则难以解决这种包含多种数据类型的多输出仿真模型可信度评估问题。
依据系统输出的数据类型,将仿真输出和参考输出分别如图5~10所示。邀请专家通过观察并分析各类数据特征,进而评定得到的各仿真输出量相对参考输出的符合度如表2所示。
为了确定各仿真输出的权重,专家对4个输出的重要性程度比值进行评定结果如表3所示。其中,ω1 代表导弹位置的权重;ω2代表弹道倾角的权重;ω3代表弹道倾角速度的权重;ω4代表脱靶量的权重。
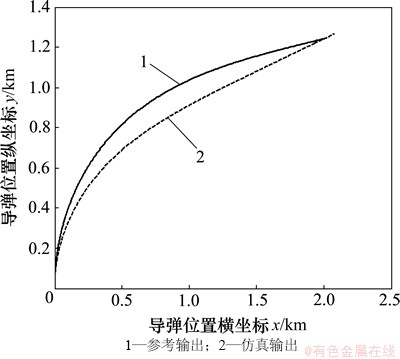
图5 导弹的位置
Fig. 5 Position of missile
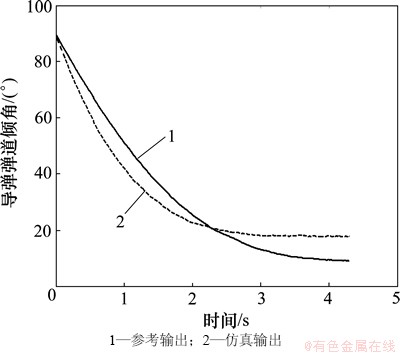
图6 导弹的弹道倾角
Fig. 6 Trajectory inclination angle of missile
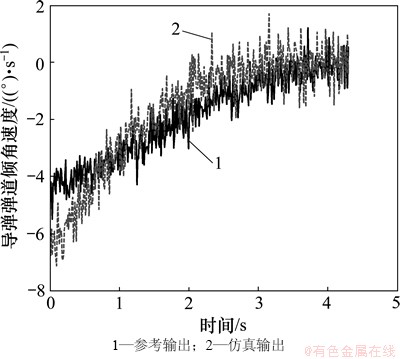
图7 导弹的弹道倾角速度
Fig. 7 Trajectory inclination angular velocity of missile
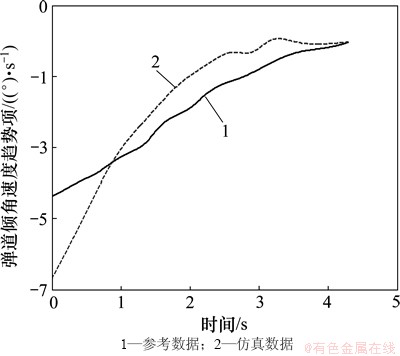
图8 弹道倾角速度趋势项
Fig. 8 Trend item of trajectory inclination angle
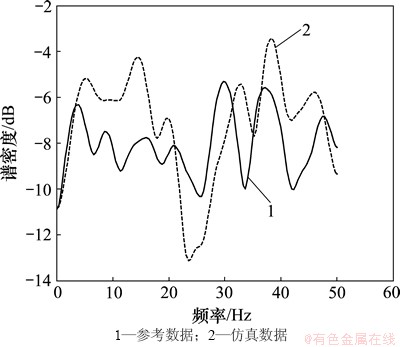
图9 弹道倾角速度平稳项的谱密度
Fig. 9 Spectrum density of stationary item of trajectory inclination angle
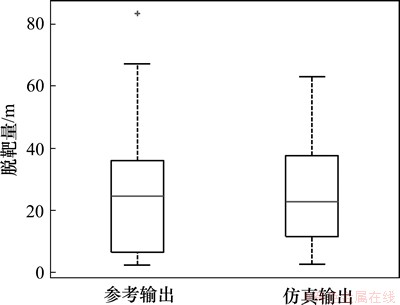
图10 脱靶量的箱线图
Fig. 10 Box plots of miss distance
依据式(7)~(14),得到权重如下:
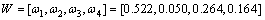 (26)
(26)
依据表2中的符合度评定结果,利用式(18)~(22)
表2 符合度评定结果
Table 2 Evaluation result of consistency degree
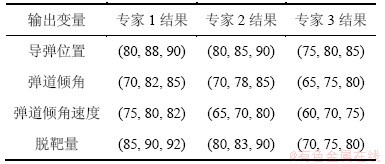
得模糊关系矩阵如下:
 (27)
(27)
依据W和R,采用式(23),得到综合结果为:
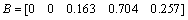 (28)
(28)
进一步,采用式(24)去模糊化,得到仿真输出相对参考输出的一致性程度为:
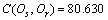 (29)
(29)
通过评估结果可以看出:该仿真模型具有较好的可信程度。对图5~10中的数据进行直观分析可知:仿真输出的导弹位置和脱靶量相对参考数据的符合度较好;仿真输出的导弹弹道倾角及过载相对参考数据的符合度一般。由式(26)可知:导弹位置的权重较大,表明它的仿真输出符合度对仿真输出一致性影响较大,由于相应的仿真输出符合度较好,所以最后综合得到的仿真输出一致性程度也不会差。虽然导弹的弹道倾角及过载相对参考数据的符合度一般,但是由于它们的权重都较小,且导弹倾角的权重为最小,所以它们的仿真输出符合度不太会对仿真输出一致性程度造成不好的影响。通过上述分析表明,式(29)所得到的仿真输出一致性程度评估结果是合理的。
表3 各输出分量重要性程度比值评定结果
Table 3 Evaluation result of important degree ratio of outputs

5 结论
(1) 研究了如何利用带有不确定性的专家意见得到仿真模型可信度,同时使得结果准确,且方法便于实际应用。
(2) 首先分析了专家意见的特点,采用三角模糊数对其描述;然后将系统输出分为静态、缓变和速变三类数据,并分别直观地将各自数据特征呈现给专家,进而得到每个仿真输出分量相对参考输出的符合度;进一步采用基于三角模糊数的层次分析法得到各仿真输出分量的权重;最后基于模糊综合评判法综合各仿真输出分量的符合度得到仿真输出的一致性程度。
(3) 在实例应用中,利用本文方法有效地评估了某导弹的比例导引系统仿真模型的可信度。下一步工作研究如何对仿真模型验证过程中的专家知识进行提取、存储和再利用。
参考文献:
[1] White K P, Ingalls R G. Introduction to simulation[C]// Proceedings of the 2009 Winter Simulation Conference. Austin, 2009: 12-23.
[2] Sanchez S M. Better than a petaflop: The power of efficient experimental design[C]// Proceedings of the 2008 Winter Simulation Conference. Miami, 2008: 73-84.
[3] 李云峰. 数字仿真模型的校核、验证和确认[J]. 中南大学学报(自然科学版), 2004, 35(2): 273-276.
LI Yunfeng. Verification, validation and accreditation on digital simulation model[J]. Journal of Central South University (Natural Science), 2004, 35(2): 273-276.
[4] 杨惠珍, 康凤举. 水下航行器制导仿真的校核、验证和确认技术[J]. 系统工程与电子技术, 2002, 24(9): 56-59.
YANG Huizhen, KANG Fengju. Study on verification, validation and accreditation of control and guidance simulation for underwater vehicle[J]. Systems Engineering and Electronics, 2002, 24(9): 56-59.
[5] Naylor T H, Finger J M. Verification of computer simulation models[J]. Management Science, 1967, 14(2): 92-101.
[6] Mckenny J L. Critique of verification of computer simulation models[J]. Management Science, 1967, 14(2): 55-59.
[7] Kheir N A, Holmes W M. On validating simulation models of missile systems[J]. Simulation, 1978, 30(4): 93-103.
[8] 吴静, 吴晓燕, 陈永兴, 等. 基于改进灰色关联分析的仿真模型验证方法[J]. 系统工程与电子技术, 2010, 32(8): 1677-1679.
WU Jing, WU Xiaoyuan, CHEN Yongxing, et al. Validation of simulation models based on improved grey relational analysis[J]. Systems Engineering and Electronics, 2010, 32(8): 1677-1679.
[9] Damborg M J. An example of error analysis in dynamic model validation[J]. Simulation, 1985, 44(6): 301-305.
[10] 刘藻珍. 基于飞行试验数据的仿真模型验证方法的研究[J]. 系统仿真学报, 2002, 14(3): 281-284.
LIU Zaozhen. Model and simulation validation based on the data of the aero experimentation[J]. Journal of system simulation, 2002, 14(3): 281-284.
[11] Balci O. Verification, validation, and certification of modeling and simulation applications[C]// Proceedings of the 2003 Winter Simulation Conference. New Orleans, 2003: 150-158.
[12] Sargent R G. Verification and validation of simulation models[C]// Proceedings of the 2010 Winter Simulation Conference. Baltimore, 2010: 166-183.
[13] 刘飞, 马萍, 杨明, 等. 复杂仿真系统可信度量化研究[J]. 哈尔滨工业大学学报, 2007, 39(1): 1-3.
LIU Fei, MA Ping, YANG Ming, et al. Research on credibility quantification of complex simulation systems[J]. Journal of Harbin institute of technology, 2007, 39(1): 1-3.
[14] 吴静, 吴晓燕, 高忠长. 复杂仿真系统建模与仿真可信性模糊综合评估[J]. 计算机集成制造系统, 2010, 16(2): 287-292.
WU Jing, WU Xiaoyan, GAO Zhongchang. Fuzzy synthesis evaluation of modeling & simulation credibility for complex simulation system[J]. Computer Integrated Manufacturing Systems, 2010, 16(2): 287-292.
[15] Vanlaarhoven P J M, Pedrycz W. A fuzzy extension of Saaty’s priority theory[J]. Fuzzy Sets and Systems, 1983, 11(1): 229-241.
[16] Magrin-Chagnollean, Baraniuk R G. Empirical mode decomposition based time-frequency attributes[C]// Proceedings of the 69th SEG Meeting. Houston, 1999: 1-4.
[17] CHANG Dayong. Applications of the extent analysis method on fuzzy AHP[J]. European Journal of Operational Research, 1996, 95(3): 649-655.
[18] CHENG Jing, TAO Jianping. Fuzzy comprehensive evaluation of drought vulnerability based on the analytic hierarchy process[J]. Agriculture and Agricultural Science Procedia, 2010, 1: 126-135.
[19] 轩永波, 黄长强, 王勇, 等. 基于灰色层次分析法的空间武器作战效能评估[J]. 空军工程大学学报(自然科学版), 2011, 12(2): 32-37.
XUAN Yong-bo, HUANG Chang-qiang, WANG Yong, et al. Effectiveness evaluation of space weapon system based on gray hierarchy method[J]. Journal of Air Force Engineering University (Natural Science Edition), 2011, 12(2): 32-37.
[20] 李祯, 杨放春, 苏森. 基于模糊多属性决策理论的语义Web服务组合算法[J]. 软件学报, 2009, 20(3): 583-596.
LI Zhen, YANG Fangchun, SU Sen. Fuzzy multi-attribute decision making-based algorithm for semantic Web service composition[J]. Journal of Software, 2009, 20(3): 583-596.
(编辑 杨幼平)
收稿日期:2013-07-17;修回日期:2013-09-03
基金项目:国家自然科学基金资助项目(61273226);国家自然科学基金委创新研究群体科学基金资助项目(61021002)
通信作者:杨明(1963-),男,吉林蛟河人,博士,教授,从事复杂系统仿真理论与方法等研究;电话:0451-86418807-8411;E-mail: mycschit@163.com