粒径及颗粒级配对离子型稀土二维入渗特性的影响
来源期刊:中国有色金属学报(英文版)2020年第6期
论文作者:郭钟群 赖远明 金解放 周尖荣 赵奎 孙政
文章页码:1647 - 1661
关键词:离子型稀土矿;粒径;颗粒级配;二维入渗;湿润锋
Key words:weathered crust elution-deposited rare earth ores; particle size; grain composition; two-dimensional infiltration; wetted front
摘 要:借助于数字图像技术开展离子型稀土二维入渗试验,通过可视化的数字图像刻画湿润体演化过程。湿润锋距离与注液时间呈现极显著的幂函数关系,随着细颗粒含量的增加,湿润锋距离逐渐减小,入渗曲线变平缓;在注液初期,水平方向湿润锋距离比垂直方向湿润锋距离大,随着注液时间推移,垂直方向湿润锋距离逐渐接近水平方向湿润锋距离。湿润锋运移速率呈现出三阶段的变化规律,在相同历时,湿润锋运移速率随着粗颗粒含量的增加而增大。定义向速比表征不同方向湿润锋运移速率的比值。在注液初期,水平方向湿润锋运移速率快,随着时间的推进,垂直方向湿润锋运移速率逐渐接近水平方向。建立稳定入渗率与特征粒径、不均匀系数和曲率系数的线性经验关系,为反演原地浸矿时的稳定入渗率提供理论依据。
Abstract: The two-dimensional infiltration experiment was carried out by means of digital image technology. The evolution process of the wetting body was described. The wetted front distance and the time show a very significant power function relationship. The horizontal wetted distance is larger than the vertical wetted distance in the initial stage. Then, the vertical distance of the wetted body gradually approaches to the horizontal distance. The infiltration distance decreases as the content of fine particles increases. The wetted front migration rate curve shows a three-stage change law, and it increases with the increase of coarse particle content. The directional velocity ratio is defined. The initial value of horizontal infiltration rate is larger than that of vertical one, and then the vertical infiltration rate is gradually close to the horizontal value. The empirical relationship between the characteristic particle size and the stable infiltration rate is established, which provides a theoretical basis for the prediction of the stable infiltration rate in in-situ leaching.
Trans. Nonferrous Met. Soc. China 30(2020) 1647-1661
Zhong-qun GUO1, Yuan-ming LAI2, Jie-fang JIN1, Jian-rong ZHOU1, Kui ZHAO3, Zheng SUN1
1. School of Architectural and Surveying & Mapping Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China;
2. Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences, Lanzhou 730000, China;
3. Jiangxi Key Laboratory of Mining Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China
Received 10 October 2019; accepted 28 April 2020
Abstract: The two-dimensional infiltration experiment was carried out by means of digital image technology. The evolution process of the wetting body was described. The wetted front distance and the time show a very significant power function relationship. The horizontal wetted distance is larger than the vertical wetted distance in the initial stage. Then, the vertical distance of the wetted body gradually approaches to the horizontal distance. The infiltration distance decreases as the content of fine particles increases. The wetted front migration rate curve shows a three-stage change law, and it increases with the increase of coarse particle content. The directional velocity ratio is defined. The initial value of horizontal infiltration rate is larger than that of vertical one, and then the vertical infiltration rate is gradually close to the horizontal value. The empirical relationship between the characteristic particle size and the stable infiltration rate is established, which provides a theoretical basis for the prediction of the stable infiltration rate in in-situ leaching.
Key words: weathered crust elution-deposited rare earth ores; particle size; grain composition; two-dimensional infiltration; wetted front
1 Introduction
Weathered crust elution-deposited rare earth ores (also referred as ion-absorbed type rare earth ores) are rich of heavy rare earth elements and special world-concerned combat readiness resources in China. They mainly distribute in south of Jiangxi Province, northern Guangdong, south of Hunan Province and west of Fujian Province [1-3]. In these ores, rare earth elements which are adsorbed onto the clay minerals through hydrated cations or hydroxyl hydrated cations are difficult to be enriched by conventional selecting technique. Currently, rare earth elements are mainly extracted by solution mining [4]. In solution mining, solution of salt leaching agent is injected into the clay ore, thus triggering chemical replacement reaction between ammonium ions in the leaching solution and rare earth ions adsorbed on the clay. Rare earth leachate infiltrates in ore body, then converges at foot of a mountain through the effusion ditch or collection roadway, purified and deposited in hydrometallurgical plant, and finally recovers resources [5]. Infiltration of leaching solute in clay ore body has become a key factor that restricts resource leaching rate and leaching speed [6,7].
Since weathered crust elution-deposited rare earth ores have an extensive distribution and there are differences in properties of clay from different ores, infiltration performances of soil mass vary. Particle size, sorting and rounding, and grain composite are important factors that influence infiltration ability of fluid. Different particle size and grain composition may change pore structure and infiltration characteristics in soil, influence moving path of water in soils, and restrict or accelerate infiltration of water [8]. Hence, studying the influencing law of particle size and grain composition on infiltration of weathered crust elution-deposited rare earth ores is the key to calculate infiltration rate. The calculated infiltration rate is conducive to predict and timely regulation of leaching process has important significance to improve leaching rate of rare earth resources.
Many scholars have carried out a great deal of studies on influence of particle size and grain composition on water migration in soil mass [9-12]. YIN et al [13] carried out a capillary experimental study on solution with different particle sizes of ore and found that solution in the stock heap formed by large ores was affected by capillary effect slightly, while solution in stock heap with a high proportion of fine particles was influenced by capillary effect greatly. LIU et al [14] tested infiltration characteristics of sandy soil with different particle sizes by a horizontal earth-pillar infiltration method and found that particle size of sand was proportional to infiltration performance. There is a power functional relationship between advancing rate of the wetting peak and the infiltration distance. ZHANG et al [15] investigated influence of different particle sizes of perlites on water content in soil mass through a water infiltration test and found that large and moderate particle sizes could promote infiltration of water in soil mass. Based on an orthogonal test, WANG et al [16] pointed out that permeability coefficient of coarse-grained soils was positively correlated with eigenvalue of grain composition (d20) and coefficient of curvature (Cc). GUO et al [17] studied the influence of one- dimensional saturated permeability coefficient of the maximum particle size of weathered crust elution-deposited rare earth ores and found that saturated permeability coefficient was positively correlated with the maximum particle size. Currently, studies on infiltration of weathered crust elution-deposited rare earth ores were mainly focused on one-dimensional infiltration of soil mass, but few have discussed two-dimensional infiltration characteristics. Two-dimensional infiltration law conforms to engineering practices better. Therefore, studying two-dimensional infiltration characteristics of weathered crust elution-deposited rare earth ores and corresponding influencing factors is of important significance. With the high-speed development of high-resolution digital photo- graphic equipments and computer-based image processing technology [18,19], studies on scientific problems of geotechnical engineering based on digital image technology become increasingly mature [20-22].
In this study, a two-dimensional infiltration test was carried out with rare earth from Zudong Rare Earth Ore in Longnan County, Jiangxi Province, China. Infiltration data were collected based on digital image technology. Influencing laws of particle size and grain composition on shape of wetted body, two-dimensional migration distance of wetting peak, infiltration rate and mean infiltration rate were investigated. The empirical calculation formula of distance of wetting peak and infiltration rate was deduced, aiming to provide theoretical references in parameter design for liquid injection well network during in-situ leaching process of weathered crust elution-deposited rare earth ores and increase leaching rate of rare earth resources.
2 Modeling of leaching system with permeability and particle size
According to Darcy’s law, a differential element along streamline direction (S) is shown in Fig.1. This differential element is ds long and the cross-section area of the differential element is dA. If the inertia force of water flow can be neglected, there are three forces acting on the element, which are pore water pressure at two ends, dead load of water flow in pores and frictional resistance of water flow by the uniform sphere (equivalent particles) (F).
The equilibrium of three forces along the soil-pillar infiltration direction is
pndA-(p+dp)ndA-γndsdAsin θ-F=0 (1)
where p is the pore water pressure, dp is the increment of pore water pressure, n is the porosity of soil mass, γ is the volumic mass of water, and θ is the included angle between streamline direction and the horizontal direction.
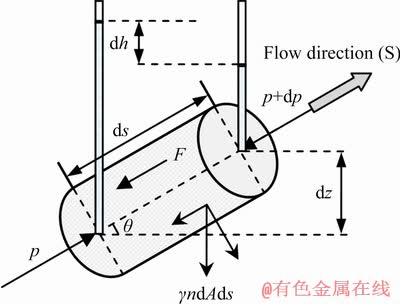
Fig. 1 Differential element along streamline direction
According to geometric relationship, it can be known that
sin θ=dz/ds (2)
Due to influence of energy difference, water moves from the high-energy position to the low-energy position in porous medium. Energy of water flow is generally expressed by water head:
h=z+p/γ (3)
Through integration of Eq. (3), we can get
dp=γ(dh-dz) (4)
Bring Eqs. (2) and (4) into Eq. (1), and get
nγdAdh+F=0 (5)
According to Stokes law, the resistance that a spherical particle overcomes in laminar flow is
F′=6πμur (6)
where μ is the dynamic viscosity of water, u is the local actual speed along circumferential direction of particles, and r is the radius of spherical particles.
If there are N particles in a soil-pillar and a spherical coefficient (β, β=π/6 for spheres) is introduced, the total resistance is
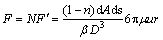 (7)
(7)
where D is diameter of a spherical particle, and D=2r.
The relationship between mean seepage speed on a section and local practical speed along circumferential direction of single particle is
v=nu (8)
where v is seepage velocity.
Combining Eqs. (5), (7) and (8), we get
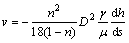 (9)
(9)
The hydraulic gradient is
J=-dh/ds (10)
Bring Eq. (10) into Eq. (9), and get
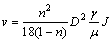 (11)
(11)
Let C=n2/[18(1-n)], where C is a shape factor which is related with the porosity of medium, particle shape and arrangement mode. Therefore, the infiltration speed can be expressed as
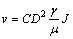 (12)
(12)
According to Darcy law, the relationship between infiltration speed and hydraulic gradient is
v=kJ (13)
where k is permeability coefficient.
It can be seen from Eqs. (12) and (13) that the relationship between permeability coefficient and properties of media and fluid is
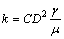 (14)
(14)
Based on above analysis, permeability coefficient is determined by two aspects: one is properties of porous media (CD2) and the other is properties of the liquid (γ/μ). When the leaching solution is fixed (same properties of fluid) in leaching of weathered crust elution-deposited rare earth ores, shape factor (C) and calculated particle size (D2) of soil mass are factors that control the infiltration. Soil mass is composed of numerous soil particles with different sizes. If soil particle shape is spherical and C exerts a small effect, particle size and grain composition are vital to infiltration effect of soil mass.
3 Two-dimensional infiltration test
3.1 Testing apparatus
To study two-dimensional infiltration characteristics of weathered crust elution-deposited rare earth ores, a set of visualized two-dimensional infiltration device was designed in this study. The whole test system was composed of a two- dimensional infiltration device and digital image collection device (Fig. 2). The two-dimensional infiltration device is composed of a Markov water bottle, soil tank, injection tube, overflow pipe and measuring cylinder. The soil tank applies a fan-column glass tank with an included angle of 30° and its vertical height and horizontal length were both 50 cm. The outer wall of the soil tank had scales vertically and horizontally. The radius of injection tube was 1 cm. The digital image collection device was composed of a Canon EOS 80D digital camera and a computer.

Fig. 2 Schematic diagram of experiment device
3.2 Test materials and method
Rare earth samples were collected from Zudong Rare Earth Ore in Longnan County, Ganzhou City, Jiangxi Province, China. Basic physical parameters of samples were tested. Density, water content, specific gravity, porosity, liquid and plastic limits and plastic index of soil samples are given in Table 1, indicating that soil samples belong to silty clay. Soil samples were dried, ground and screened. The proportion of 0.075-10 mm particles was tested to be 82.86% according to the screening method. Content of small particles (<0.075 mm) was tested by a BT-2002 laser particle size distribution instrument. Test results of screening method and laser particle size distribution were analyzed. Grain composition of rare earth samples is listed in Table 2.
Particle size and grain composition were discussed in the present study. When particle size was fixed, grain composition might be different and there might be several degrees of freedom (DOFs). In other words, several curves of grain composition can be drawn from one point. In the experiment, undisturbed remoulded soil and remoulded soils with 7 particle sizes and grain compositions were designed (Table 3). S1 was undisturbed remoulded soil, while S2-S8 were remoulded soils with 100%, 90%, 80%, 70%, 60%, 50% and 40% contents of particles smaller than 1 mm. The limiting particle size d60 was mainly used as the division sign of grain composition. Moreover, mean particle size (d50), median size (d30) and effective size (d10) were considered in this study. Particle size and grain composition of S1 are between those of S6 and S7. The grain distribution curve is shown in Fig. 3.
Coefficient of heterogeneity and coefficient of curvature of soil samples are determined according to grain composition index of soil particles. Coefficient of heterogeneity of soil is expressed by Cu:
Cu=d60/d10 (15)
The coefficient of curvature is expressed by Cc:
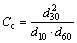 (16)
(16)
Table 1 Basic physical parameters of ores

Table 2 Grain composition of ores (wt.%)

Table 3 Soil samples with different particle sizes and gradations
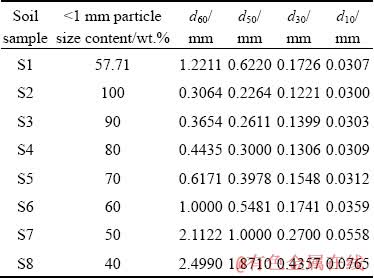
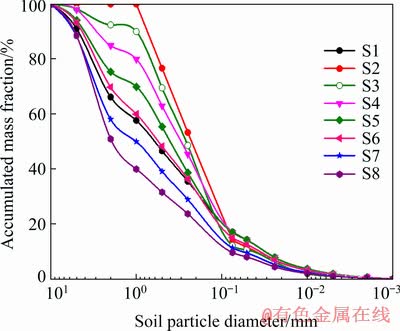
Fig. 3 Grain distribution curves of soil samples
The coefficient of heterogeneity reflects the distribution of particle size. The larger the value is, the larger range the particle size distribution has, and the better the mechanical properties are. The coefficient of curvature (Cc) depicts distribution range of grain distribution curve and reflects the overall shape of the curve. The coefficient of heterogeneity of S1-S8 is shown in Fig. 4. The coefficient of curvature is shown in Fig. 5.
The main test process is introduced as follows. Firstly, all soil samples were dried. Soil samples with different particle sizes and grain compositions were filled in the soil tanks layer by layer (5 cm of each layer) and compacted uniformly. The soil layer was roughened after compaction and then the next layer was filled. Attentions were paid to prevent vertical layering of soil mass and the height of infiltration water head was controlled to be 10 cm.
Secondly, the camera rack was adjusted to keep horizontally and make the lens of digital camera aligned with the side square plane of the soil tank. Positions of the rack were recorded for the following test to prevent the error caused by different positions of the rack.
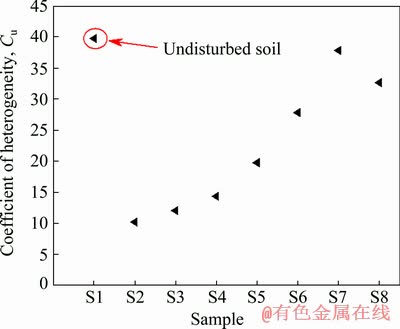
Fig. 4 Coefficient of heterogeneity of soil samples
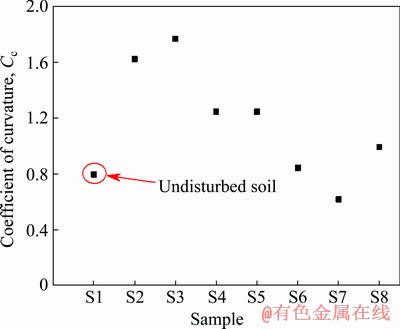
Fig. 5 Coefficient of curvature of soil samples
Finally, press the switch of water bottle to start the infiltration test. Later, the camera was started to take photos automatically at a preset interval (every 10 min in the first 3 h and every 30 min after 3 h). A computer was applied for the purpose of timing and storage of digital images. Infiltration time was set to be 10-12 h.
Since dried soil samples are light in color and wetted region has deep color, there was an evident peak before wetting. The position and shape of this wetting peak could be described clearly in digital image. To assure the accuracy of test data, each infiltration test was repeated by 3 times to lower the discreteness of test data.
4 Test results and discussion
4.1 Shape of wetted body
For the reasonable setting of parameters for injection well network for in-situ leaching of weathered crust elution-deposited rare earth ores, it is necessary to study temporal-spatial variation law of shape and size of wetted body at single-pore infiltration. Shape and size of wetted body throughout the infiltration process could be recorded clearly and accurately by digital image technology. After digital images were extracted, it generally required binaryzation or denoising filtering of digital images in order to eliminate the influence of light source and background on images and get good visualization effect [23]. In this study, images were pre-processed by Photoshop software. Since the experiment involved many groups, digital images of S1 were chosen for explanation (Fig. 6).

Fig. 6 Digital images of wetted volume with time
Obviously, there is a clear boundary (wetting peak) between filtration soil mass and non-infiltrated soil mass. Since injection hole is at the origin of a coordinate system, it can be speculated from symmetry that the wetted body is approximately an oval. In the first 180 min of infiltration, the horizontal wetting distance is significantly larger than the vertical one and the two-dimensional wetted body is an oval. As infiltration continues, the vertical wetting distance increases gradually after 360 min and it basically conforms to the horizontal wetting distance. Therefore, the two-dimensional wetted body is a sphere, indicating that the vertically downward infiltration rate is higher than the horizontal infiltration rate. According to analysis, acting force of horizontal water migration is mainly the matric potential, while the acting force of vertical water migration is attributed to gravity potential and pressure of injection water head in addition to matrix potential. When the infiltration time continues to increase, the effect of gravity potential is increased accordingly. Size of the wetted body is determined by horizontal infiltration distance and vertical infiltration distance together. Infiltration size is determined by horizontal infiltration rate and vertical infiltration rate. Mastering variation law of migration distance of the two-dimensional wetting peak and infiltration rate is of important significance to optimize parameters of the injection well network. If the well network is too dense, there will be excessive loss of leaching solution. If the well network is too loose, it is easy to form a leaching blind area of rare earth, resulting in resource waste.
Particle size and grain composition can influence size and shape of the wetted body significantly. Digital images of wetted body in S1-S8 at the same infiltration moment (t=600 min) are shown in Fig. 7. In the process of infiltration, wetted body in all samples is an oval. Given the same infiltration time, size of wetted body is positively related with content of large particles. This reflects that particle size can influence the infiltration rate of soil mass significantly.
4.2 Distance of wetting peak

Fig. 7 Digital images of soil samples at t=600 min
Since infiltration capacity of soil mass with different particle sizes and grain compositions is different, the migration distance of wetting peak is also different. The relationship between infiltration distance of the wetting peak and infiltration time of different soil samples is an important reference to determine parameters of injected well network in engineering practices and it is conducive to reasonably predict and timely regulate leaching process of weathered crust elution-deposited rare earth ores in practical engineering. Horizontal and vertical infiltration distances are two important eigenvalues of two-dimensional infiltration of the wetted body. According to data from digital images, distance of wetting peak at different moments can be acquired accurately. It can be seen from Ref. [2] that infiltration model of power function can describe the relationship between infiltration distance of weathered crust elution-deposited rare earth ores and time accurately. Such relationship and its fitting curve are presented in Fig. 8. Clearly, particle size can influence both horizontal and vertical infiltration distance significantly. Given the same infiltration time, infiltration distance is negatively related with content of fine particles and the infiltration curve becomes stable, indicating that many micro-particles can block water channel and increase the resistance againt water migration. With the increase of content of coarse particles, the infiltration distance increases accordingly. In other words, pore channels among different particles increase and the connectivity enhances with the increase of content of coarse particles, thus promoting the migration of water in soils.
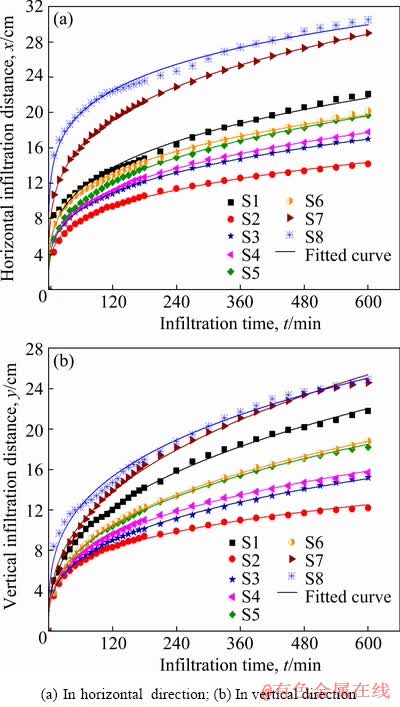
Fig. 8 Wetted front distance with time
The power functional relation between distance of wetting distance and time is
H=atb (17)
where H is the distance of wetting peak (cm) and t is the infiltration time (min). a is an empirical infiltration parameter and it refers to the infiltration distance from the beginning moment to the end of the last unit time of infiltration. The numerical value of a is equal to infltration rate at the end of the first unit time and it can reflect the infiltration capacity to a large extend. b is an empirical infiltration index and reflects the changes of soil infiltration capacity. Fitting results of relationship between horizontal infiltration and duration of infiltration as well as the relationship between vertical infiltration and duration of infiltration are given in Table 4 and Table 5.
Table 4 Fitting results of relationship between horizontal wetted front and duration of infiltration

Table 5 Fitting results of relationship between vertical wetted front and duration of infiltration
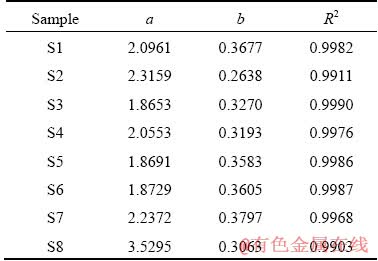
Higher decisive coefficient (R2) of the regression equation indicates better fitting result of the simulation equation. According to fitting results, R2 of the fitting equation is 0.9860-0.9995, averaging at 0.9961. This reflects that the fitting effect is good and fitted value is very close to measured value. This equation can depict the relationship between migration distance of the wetting peak and time in the infiltration process of weathered crust elution-deposited rare earth ores. Since S1 is undisturbed remoulded soil with particle size and grain composition similar with those of S6, the fitting parameter (a) of S1 is also close to that of S6. The content of fine particle in S2-S8 decreases gradually, while the content of coarse particle increases gradually. In Table 4, a increases gradually with the increase of content of coarse particles and it reflects the positive relationship between initial horizontal infiltration distance and content of coarse particles. Value of b ranges between 0.2519 and 0.2840 except for a small value (only 0.1776) in S8. It is relatively stable, indicating that seepage in late stage of infiltration is relatively stable. Matric potential weakens after soil saturation. The bending degree of the soil infiltration path after saturation and the pores influence the seepage slightly. It can be seen from Table 5 that with the increase of content of coarse particles, a decreases firstly and then increases gradually. This reflects that the initial vertical infiltration distance is senstive to other factors in addition to particle size and grain composition, because soil water potential involves collaboration of gravitational potential and pressure potential except matric potential. b ranges between 0.2638 and 0.3797 and it is relatively stable, similar with that in the horizontal direction.
4.3 Migration speed of wetting peak
The relation curves between horizontal migration speed of wetting front of S1-S8 and time are shown in Fig. 9. In initial infiltration stage, migration speed of wetting peak of different samples is high and it begins to decrease quickly. With the increase of injection time, migration speed of wetting peak changes slightly and tends to be stable. Later, it enters into the stable infiltration stage. In the view of infiltration time, the wetting peaks of all soil samples migrate very quickly in the first 10 min, 0.42-0.84 cm/min in the first 10 min for S1-S6, 1.07 cm/min for S7 and 1.52 cm/min for S8. Migration speed of wetting peaks of all samples drops quickly to 0.02-0.05 cm/min from 10 to 60 min and then drops at a stable rate from 60 to 120 min. Finally, the migration speed of wetting peaks becomes stable at about 0.01 cm/min after 120 min. According to numerical value of migration speed of wetting peaks from the initial infiltration stage, it is positively related with the content of coarse particles. Given a relatively high content of coarse particles, the compactness of soil mass decreases and the pore channel is relatively large, so that water can flow quickly in the pore channel. As injection infiltration continues, particles migrate and some small particles may block pores gradually, thus decreasing the migration speed of wetting peak. When the upper wetted soil mass is saturated, particle migration enters into a relatively stable stage. Migration speed of wetting peak after 120 min is stablized. The variation law of vertical migration speed of wetting peaks is basically consistent with that of horizontal migration speed.
According to the analysis, the Kostiakov infiltration model can depict the relationship between migration rate and time in the experiment:
v=At –B (18)
where v is the migration speed of wetting peaks (cm/min), t is infiltration time (min), and A and B are empirical parameters.
In regression equations fitted by Kostiakov model of S1-S8, the decisive coefficient R2 is 0.9593-0.9882, which indicates the good fitting result. A ranges between 9.4 and 832.2 and B is between 1.36 and 2.74. Clearly, A and B are positively related with the content of coarse particles.
Directional velocity ratio (β) is defined to be the ratio between horizontal migration speed of wetting peak and the vertical migration speed of wetting peak at the same moment:
β=vx/vy (19)
where vx is the horizontal migration speed of wetting peak (cm/min) and vy is the vertical migration speed of wetting peak (cm/min).
The directional velocity ratio reflects the moving speed of the wetting peak along the horizontal and vertical directions and it shows the flatness of the oval wetted body. When β>1, the wetted body is a flat ellipsoid. When β<1, the wetted body is developed from a flat ellipsoid to a sphere. When β=1, the wetted body is changed into an ellipsoid where the horizontal direction is a short axis and the vertical direction is the long axis. In this experiment, directional velocity ratios of samples with different particle sizes and grain compositions are shown in Fig. 10.
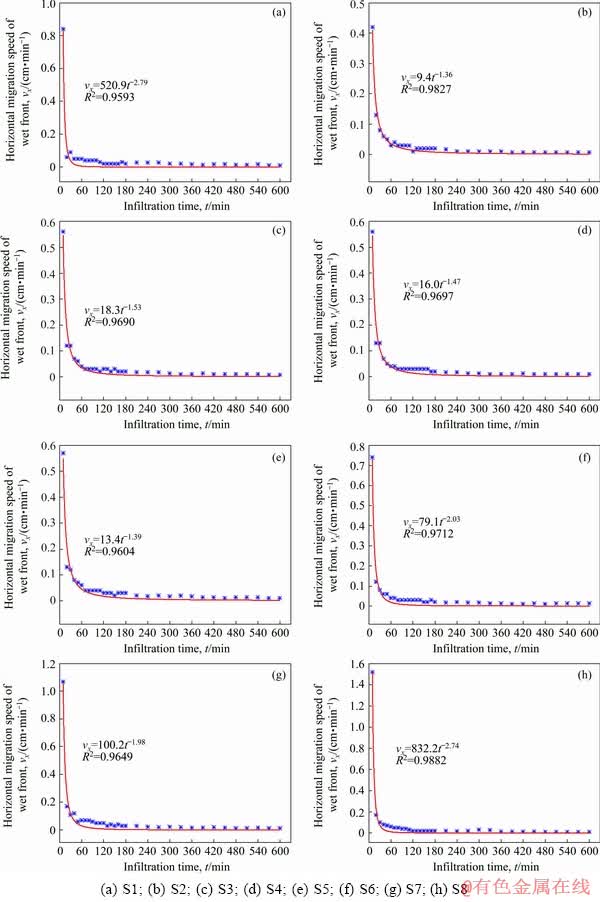
Fig. 9 Horizontal migration speeds of wetting front of S1-S8 with time
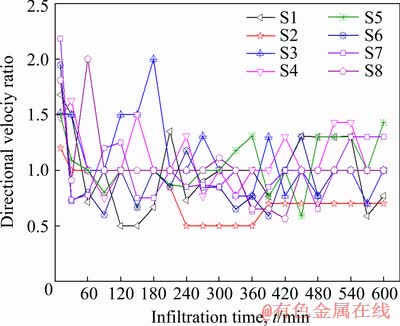
Fig. 10 Directional velocity ratios of samples
It can be seen from Fig. 10 that in the initial stage of infiltration (t=10 min), the directional velocity ratio of S2 is 1.2 and that of other soil samples ranges between 1.5 and 2.2, indicating that horizontal migration speed of the wetting peak is significantly higher than the vertical one and the wetted body is a flat ellipsoid. According to analysis, matrix suction is the main power for water migration in the initial infiltration stage. Meanwhile, the vertical compactness is better and horizontal migration speed of water is higher due to the interfacial effect. As injection infiltration continues, directional speed ratio of all soil samples declines gradually and becomes stable after 420 min. The directional speed ratio of S2 and S3 is stabilized at about 0.7-1, while the directional speed ratio of S4-S8 is stabilized at about 1-1.3. This implies that vertical migration speed of the wetting peak becomes higher or equal to horizontal one gradually and the wetted body becomes spherical gradually. It can be concluded from analysis that as injection infiltration goes on, matric potential gradient in soil declines gradually. In horizontal direction, the wetting peak further moves far away from the saturation region and the driving force provided by matric potential gradient decreases continuously. On the contrary, the total vertical potential is higher than the horizontal matric potential, which is related with the collaborative effect of matric potential, pressure potential of injection water head and gravitational potential. As a result, the vertical migration speed of the wetting speed approaches to and even exceeds the horizontal one. When the infiltration continues, the saturation circle of moisture content in soil expands gradually and migration of water to surrounding soils decelerates gradually and finally tends to be stable.
4.4 Average infiltration rate
The relation curves between average infiltration rates along the horizontal and vertical directions of different oil samples and infiltration time are shown in Fig. 11. The average infiltration rate presents three variation stages. In the first stage (in the first 60 min), the average infiltration rate is the highest in the initial infiltration stage and then declines quickly. In the second stage (30-360 min), the average infiltration rate declines at a stable rate. In the third stage (beyond 360 min), the average infiltration rate becomes stable and it is close to a fixed value. According to analysis, the wetted body has a small volume and the matric potential gradient is relatively high in the first stage, which is in favor of quick infiltration of water. Later, the infiltration rate drops quickly. The initial infiltration rate along the horizontal direction is 0.5-1.5 cm/min and then drops to 0.15-0.33 cm/min. The initial infiltration rate along the vertical direction is 0.4-0.8 cm/min and then declines to 0.12-0.20 cm/min quickly. In the second stage, the wetted body expands continuously and moisture content increases significantly, while the matric potential gradient declines greatly, thus resulting in gradual reduction of average infiltration rate. The horizontal average infiltration rate decreases by 0.04-0.08 cm/min and the vertical average infiltration rate decreases by 0.03-0.06 cm/min. In the third stage, moisture content in surrounding soil mass of soil-water interface tends to be saturated with the continuous water infiltration and the average infiltration rate finally tends to be stable (0.03-0.05 cm/min). In other words, it enters into a relatively stable infiltration state.
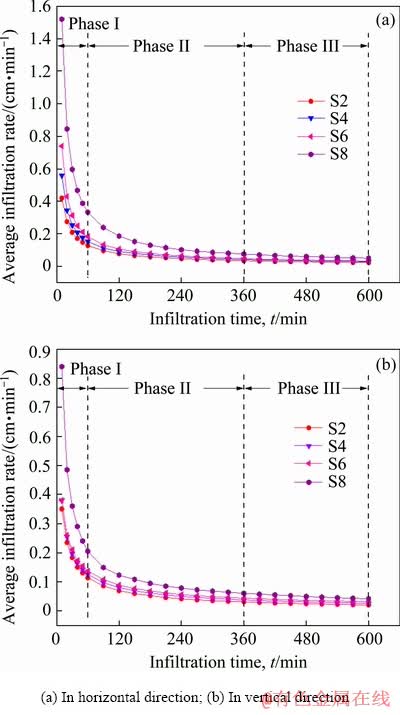
Fig. 11 Average infiltration rate of samples with time
When the infiltration time is fixed, the average infiltration rate of soil mass is proportional to particle size. This reflects that the average infiltration rate of soil samples increases with the increase of content of coarse particles. It is found from analysis that it is easier to form large pores in soil particles to facilitate water migration when there are more large particles. However, the contact angle of soil particles decreases with the increase of content of fine particles, thus forming smaller pores to block channel for downward water flow. Capillary action of small pores is stronger and more water rises along the capillary tubes.
When soil mass develops approximately from saturation to saturation, the infiltration rate tends to be stable infinitely. Stable infiltration rate is a key factor that influences the injection infiltration of weathered crust elution-deposited rare earth ores and it is one of parameters to measure difficulties for flow of leaching mother liquor. Grain composition influences stable infiltration rate to a large extent. Typical particle size (characteristic particle), the coefficient of heterogeneity and coefficient of curvature are important parameters to represent grain composition.
According to correlation theory, simpler formulas have higher application values. If the regression equation is linearly correlated, it is more practical. To disclose the relationship between grain composition of weathered crust elution-deposited rare earth ores and stable infiltration rate, the fitting relations of limiting particle size (d60), average particle size (d50), medium particle size (d30) and effective particle size (d10) with horizontal and vertical stable infiltration rates were analyzed (Fig. 12).
Clearly, typical particle size presents a good linear relationship with stable infiltration rate along both horizontal and vertical directions. The empirical formula is
is=m+nd (20)
where is is the stable infiltration rate (cm/min), d is typical particle size (cm), and m and n are fitting parameters.

Fig. 12 Relation between typical particle size and stable infiltration rate
According to fitting results, d60 presents the highest correlation with is and the corresponding R2 is 0.9643 and 0.8810 in horizontal and vertical directions, respectively. The d50 presents the second highest correlation with is and the corresponding R2 is 0.8616 and 0.7361. The d30 and d10 have very close numerical value and their R2 is slightly low (0.6269-0.7971). In the view of correlation, d60 and d50 can influence stable infiltration rate more compared with other particle sizes.
Based on Eq. (14), calculating particle size D2 is the decisive factor that controls the seepage. So, linear correlations of 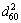 ,
, 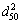 ,
, 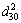 and
and  with stable infiltration rate are analyzed (Fig. 13). There is certain linear relationship between d2 and is. The empirical formula is
with stable infiltration rate are analyzed (Fig. 13). There is certain linear relationship between d2 and is. The empirical formula is
is=m′+n′d2 (21)
where m′ and n′ are fitting parameters.
By comparing Fig. 12 and Fig. 13, it is found that decisive coefficient in linear analysis (Fig. 13) is generally lower than that in Fig. 12. This reflects that the correlation between d2 and is is lower than that between d and is. In different d2, 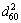 shows the highest correlation with is, and the corresponding R2 is 0.9045 and 0.7392 in two directions. In a word, d60 is the most important characteristic particle size that influences stable infiltration rate.
shows the highest correlation with is, and the corresponding R2 is 0.9045 and 0.7392 in two directions. In a word, d60 is the most important characteristic particle size that influences stable infiltration rate.

Fig. 13 Relation between square of typical particle size and stable infiltration rate
To analyze the influence of grain composition on the infiltration comprehensively, the relations of stable infiltration rate with coefficient of heterogeneity and coefficient of curvature are further discussed. According to linear correlation between stable infiltration rate and coefficient of heterogeneity in test data, there is a positive linear correlation between stable infiltration rate and coefficient of heterogeneity. The higher the coefficient of heterogeneity is, the more stable the infiltration rate will be (Fig. 14).
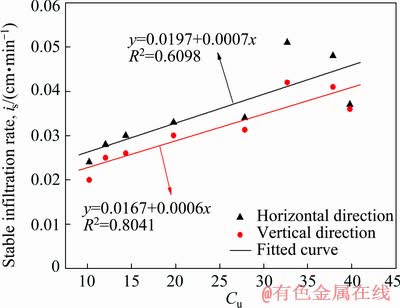
Fig. 14 Relation between stable infiltration rate and coefficient of heterogeneity
The empirical formulas of stable infiltration rate and coefficient of heterogeneity are as follows.
In the horizontal direction:
is=0.0197+0.0007Cu (22)
In the vertical direction:
is=0.0167+0.0006Cu (23)
Stable infiltration rate has a negative linear relationship with the coefficient of curvature. The permeability coefficient is smaller when the coefficient of curvature is higher (Fig. 15).
The empirical formulas of stable infiltration rate and coefficient of curvature are as follows.
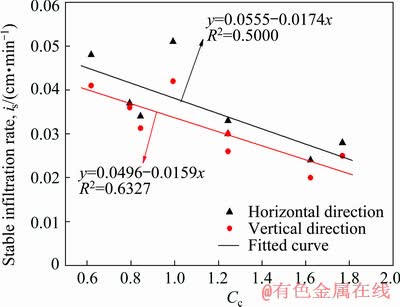
Fig. 15 Relation between stable infiltration rate and coefficient of curvature
In the horizontal direction:
is=0.0555-0.0174Cc (24)
In the vertical direction:
is=0.0496-0.0159Cc (25)
R2 of correlation between stable infiltration rate and coefficient of heterogeneity are 0.6098 and 0.8041 in horizontal and vertical directions, respectively. R2 of correlation between stable infiltration rate and coefficient of curvature are 0.5000 and 0.6327 in two directions. This reflects that the stable infiltration rate is more related with coefficient of heterogeneity than coefficient of curvature. The vertical correlation is stronger than horizontal correlation. With respect to correlations with coefficient of heterogeneity and coefficient of curvature, stable infiltration rate is actually related with d60, d30 and d10.
5 Conclusions
(1) According to theoretical studies, when the leaching solution is fixed, permeability coefficient is closely related with shape factor of soil particles and calculated particle size during in-situ leaching of weathered crust elution-deposited rare earth ores. If soil particles are approximately spherical and the influence of shape factor is neglected, infiltration characteristics are determined by particle size and grain composition of soils.
(2) A two-dimensional infiltration test of weathered crust elution-deposited rare earth ores is carried out based on digital image technology. The wetted body is approximately oval according to visualized test results. Moreover, the evolution process of wetted body is depicted intuitively. When the infiltration time is fixed, the wetted body expands with the increase of content of coarse particles.
(3) There is an extremely significant power functional relationship between distance of wetting peak and time. Given the same infiltration time, the infiltration distance declines with the increase of content of fine particles and the infiltration curve becomes increasingly stable. As injection infiltration continues, the vertical distance of wetted body is increasingly close to the horizontal distance.
(4) Migration speed of wetting peak in the initial stage is the highest and then it drops from a high rate to a low rate. Finally, it becomes stable. A directional velocity ratio is defined. In the injection infiltration, the directional velocity ratio decreases and approaches to 1, indicating the high horizontal infiltration rate in the initial stage. Subsequently, the vertical infiltration rate approaches to and even exceeds the horizontal infiltration ate.
(5) The average infiltration rate reaches the maximum in the initial stage. Later, it drops at a changing rate from high to low. Finally, it tends to be stable. The empirical formulas of relations between characteristic parameters of grain composition and stable infiltration rate are constructed, finding that the linear correlation between d60 and stable infiltration rate is the highest. Research results provide theoretical references for inversion of stable infiltration rate of weathered crust elution-deposited rare earth ores and have certain application values.
References
[1] ZHANG Zhen-yue, HE Zheng-yan, YU Jun-xia, XU Zhi-gao, CHI Ru-an. Novel solution injection technology for in-situ leaching of weathered crust elution-deposited rare earth ores [J]. Hydrometallurgy, 2016, 164: 248-256.
[2] GUO Zhong-qun, LAI Yuan-ming, ZHAO Kui, JIN Jie-fang, WANG Guan-shi. Influence range of single hole injection of ionic rare earth for constant head [J]. The Chinese Journal of Nonferrous Metals, 2018, 28(9): 1918-1927. (in Chinese)
[3] TIAN Jun, YIN Jing-qun, CHEN Kai-hong, RAO Guo-hua, JIANG Min-tao, CHI Ru-an. Optimisation of mass transfer in column elution of rare earths from low grade weathered crust elution-deposited rare earth ore [J]. Hydrometallurgy, 2010, 103: 211-214.
[4] CHI Ru-an, TIAN Jun. Weathered crust elution-deposited rare earth ores [M]. New York: Nova Science Publishers, 2008.
[5] TIAN Jun, YIN Jing-qun, CHI Ru-an, RAO Guo-hua, JIANG Min-tao, OUYANG Ke-xian. Kinetics on leaching rare earth from the weathered crust elution-deposited rare earth ores with ammonium sulfate solution [J]. Hydrometallurgy, 2010, 101: 166-170.
[6] LONG Ping, WANG Guan-shi, TIAN Jun, HU Shi-li, LUO Si-hai. Simulation of one-dimensional column leaching of weathered crust elution-deposited rare earth ore [J]. Transactions of Nonferrous Metals Society of China, 2019, 29(3): 625-6336.
[7] ZHANG Zhen-yue, SUN Ning-jie, HE Zheng-yan, CHI Ru-an. Local concentration of middle and heavy rare earth elements in the col on the weathered crust elution-deposited rare earth ores [J]. Journal of Rare Earths, 2018, 36(5): 552-558.
[8] LIU Yi-fei, ZHENG Dong-sheng, YANG Bing, ZHU Bing, SUN Ming-xiang. Microscopic simulation of influence of particle size and gradation on permeability coefficient of soil [J]. Rock and Soil Mechanics, 2019, 40(1): 403-412. (in Chinese)
[9] CAI Yuan-qiang, ZHANG Zhi-xiang, CAO Zhi-gang, YAN Shu-hao. Mesoscopic numerical simulation for suffusion process of gap-graded sandy soil [J]. Journal of Central South University (Science and Technology), 2019, 50(5): 1144-1153. (in Chinese)
[10] REN Yu-bin, WANG Yin, YANG Qing. Effects of particle size distribution and shape on permeability of calcareous sand [J]. Rock and Soil Mechanics, 2018, 39(2): 491-497. (in Chinese)
[11] SHEN P, ZHANG L M, ZHU H. Rainfall infiltration in a landslide soil deposit: Importance of inverse particle segregation [J]. Engineering Geology, 2016, 205: 116-132.
[12] SEKSAN S, PHADUNGSAK R, PREMPREEYA M. Comparison of Stefan model with single-phase model of water infiltration process in unsaturated porous media (theory and experiment) [J]. Journal of Hydrology, 2013, 497: 145-151.
[13] YIN Sheng-hua, CHEN Xun, JIANG Li-chun. Effect of ore particle size on solution capillary seepage in ore heaps [J]. Chinese Journal of Engineering, 2015, 37(5): 561-567. (in Chinese)
[14] LIU Xin-ping, ZHANG Tong-hui, HE Yu-hui, ZHAO Ha-lin, ZHAO Xue-yong, ZHAO Wei, LUAN Tian-xin, SHAN Li. Water diffusivity of sandy soils of different particle sizes [J]. Arid Land Geography, 2008, 31(2): 249-253. (in Chinese)
[15] ZHANG Nai-yu, YAN Shuang-dui, REN Qian, WANG Chun-mei, LIU Li-jun. Water movement in soil amended with perlite particles of different sizes [J]. Journal of Irrigation and Drainage, 2019, 38(2): 22-28. (in Chinese)
[16] WANG Jun-jie, LU Xiao-zhi, QIU Zhen-feng, LIANG Yue. Experimental studies on influence factors of permeability coefficients of coarse-grained soil [J]. Hydro-Science and Engineering, 2013(6): 16-20. (in Chinese)
[17] GUO Zhong-qun, JIN Jie-fang, QIN Yan-hua, WANG Xiao-jun, ZHONG Wen, ZHAO Kui. Experimental research on one-dimensional horizontal infiltration rules of ion-adsorption rare earth [J]. Nonferrous Metals Science and Engineering, 2017, 8(2): 102-106. (in Chinese)
[18] LI Shu-cai, LIU Hong-liang, LI Li-ping, SHI Shao-shuai, ZHANG Qian-qing, SUN Shang-qu, HU Jie. A quantitative method for rock structure at working faces of tunnels based on digital images and its application [J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(1): 1-9. (in Chinese)
[19] LIU Chun, SHI Bin, ZHOU Jian, TANG Chao-sheng. Quantification and characterization of microporosity by image processing, geometric measurement and statistical methods: Application on SEM images of clay materials [J]. Applied Clay Science, 2011, 54(1): 97-106.
[20] PHILIPPE G, FRANCOISE G, LYESSE L, LAURENT V. Automated digital image processing for volume change measurement in triaxial cells [J]. Geotechnical Testing Journal, 2006, 30(2): 98-103.
[21] LI Yuan-hai, JIA Ran-xu, YANG Su. Optimized method for DSCM based on progressive displacement characteristics of geotechnical materials [J]. Chinese Journal of Geotechnical Engineering, 2015, 37(8): 1490-1496. (in Chinese)
[22] LIU Chun, XU Qiang, SHI Bin, GU Ying-fan. Digital image recognition method of rock particle and pore system and its application [J]. Chinese Journal of Geotechnical Engineering, 2018, 40(5): 925-931. (in Chinese)
[23] ZHANG Wen-jie, YAO De-sheng, SHENG Jin-chang, ZHAN Mei-li, ZHOU Zhi-rong. Application of digital image processing technology in seepage analysis [J]. Journal of Hohai University (Natural Sciences), 2009, 37(6): 731-735. (in Chinese).
郭钟群1,赖远明2,金解放1,周尖荣1,赵 奎3,孙 政1
1. 江西理工大学 建筑与测绘工程学院,赣州 341000;
2. 中国科学院 西北生态环境资源研究院,兰州 730000;
3. 江西理工大学 江西省矿业工程重点实验室,赣州 341000
摘 要:借助于数字图像技术开展离子型稀土二维入渗试验,通过可视化的数字图像刻画湿润体演化过程。湿润锋距离与注液时间呈现极显著的幂函数关系,随着细颗粒含量的增加,湿润锋距离逐渐减小,入渗曲线变平缓;在注液初期,水平方向湿润锋距离比垂直方向湿润锋距离大,随着注液时间推移,垂直方向湿润锋距离逐渐接近水平方向湿润锋距离。湿润锋运移速率呈现出三阶段的变化规律,在相同历时,湿润锋运移速率随着粗颗粒含量的增加而增大。定义向速比表征不同方向湿润锋运移速率的比值。在注液初期,水平方向湿润锋运移速率快,随着时间的推进,垂直方向湿润锋运移速率逐渐接近水平方向。建立稳定入渗率与特征粒径、不均匀系数和曲率系数的线性经验关系,为反演原地浸矿时的稳定入渗率提供理论依据。
关键词:离子型稀土矿;粒径;颗粒级配;二维入渗;湿润锋
(Edited by Bing YANG)
Foundation item: Projects (51764014, 11902127) supported by the National Natural Science Foundation of China; Project (201810407004) supported by the National Undergraduate Innovation Training Program of China; Project (GJJ180457) supported by Jiangxi Education Department, China
Corresponding author: Zhong-qun GUO; Tel: +86-15216173840; E-mail: guozhongqun_jxust@163.com
DOI: 10.1016/S1003-6326(20)65327-4

