J. Cent. South Univ. (2020) 27: 3025-3039

DOI: https://doi.org/10.1007/s11771-020-4526-4

True triaxial hydraulic fracturing test and numerical simulation of limestone

YANG Wei-min(杨为民)^{1, 2}, GENG Yang(耿阳)¹, ZHOU Zong-qing(周宗青)^{1, 2}, LI Lian-chong(李连崇)³, DING Ruo-song(丁若松)¹, WU Zhong-hu(邬忠虎)⁴, ZHAI Ming-yang(翟明洋)³

1. School of Qilu Transportation, Shandong University, Ji’nan 250061, China;

2. Geotechnical and Structural Engineering Research Center, Shandong University, Ji’nan 250061, China;

3. School of Resources and Civil Engineering, Northeastern University, Shenyang 110006, China;

4. College of Civil Engineering, Guizhou University, Guiyang 550025, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: Hydraulic fracturing, as a key technology of deep energy exploitation, accelerates the rapid development of the modern petroleum industry. To study the mechanisms of hydraulic fracture propagation and rock failure mode of the vertical well hydraulic fracturing, the true triaxial hydraulic fracturing test and numerical simulation are carried out, and the influence of the principal stress difference, water injection displacement, perforation angle and natural fracture on fracture propagation is analyzed. The results show that the fracture propagation mode of limestone is mainly divided into two types: the single vertical fracture and the transverse-longitudinal crossed complex fracture. Under high displacement, the fracturing pressure is larger, and the secondary fracture is more likely to occur, while variable displacement loading is more likely to induce fracture network. Meanwhile, the amplitude of acoustic emission (AE) waveform of limestone during fracturing is between 0.01 and 0.02 mV, and the main frequency is maintained in the range of 230-300 kHz. When perforation angle θ=45°, it is easy to produce the T-type fracture that connects with the natural fracture, while X-type cracks are generated when θ=30°. The results can be used as a reference for further study on the mechanism of limestone hydraulic fracturing.

Key words: true triaxial; hydraulic fracturing; acoustic emission; particle flow code (PFC); perforation angle; natural fracture

Cite this article as: YANG Wei-min, GENG Yang, ZHOU Zong-qing, LI Lian-chong, DING Ruo-song, WU Zhong-hu, ZHAI Ming-yang. True triaxial hydraulic fracturing test and numerical simulation of limestone [J]. Journal of Central South University, 2020, 27(10): 3025-3039. DOI: https://doi.org/10.1007/s11771-020-4526-4.

1 Introduction

Hydraulic fracturing, as a key technology of deep energy exploitation, greatly improves the permeability of deep low-permeability reservoir rock and accelerates the rapid development of the modern petroleum industry, energy extraction and other fields, showing a wide range of industrial applications [1-3]. Besides, hydraulic fracturing can lead to the phenomenon of cracking, damage expansion, and even overall instability of surrounding rocks in tunnel engineering, which brings great challenges to tunnel construction and operation [4, 5]. Therefore, it is particularly important to fully understand the law of crack growth and the failure mechanism of rock mass in the process of hydraulic fracturing.

In recent years, scientists have done a lot of research on the traditional hydraulic fracturing mechanism in terms of experiments and numerical simulations. In laboratory tests, the application of acoustic emission (AE) and CT scanning equipment has further promoted research on the formation mechanism of the 3D fracture network [6-8]. Based on the AE monitoring system and CT scanning technology, scholars further studied the spatial distribution of the hydraulic fracture networks and the optimization of fracture network structures in the fractured rock mass, and finally revealed the main controlling factors affecting the formation of complex fracture networks [9-11]. Besides, a large number of scholars have studied the relationship between fracture morphology and main control factors (the difference of principal stress, the displacement and viscosity of fracturing fluid, the perforation angle, etc), and have studied the propagation law of hydraulic fracture and rock fracture mode under different factors based on AE and other equipment [12-15]. Finally, the directional control of hydraulic fracture and the formation mechanism of fracture net are put forward.

In terms of numerical simulation, the initial research is mainly based on the assumption of a continuous medium. LIN et al [16] studied the influence of viscosity and displacement of fracturing fluid on the law of hydraulic fracture growth, and concluded that high displacement and fracturing fluid viscosity are more conducive to fracture initiation and extension. PAKZAD et al [17] investigated the influence of heterogeneity on the failure response and the absolute permeability based on ABAQUS. It was found that the post-peak permeability was to decrease with the heterogeneity level, and the scattered damage elements appeared in the models with higher degree of heterogeneity. However, there are some defects in the simulation of large deformation characteristics such as crack propagation intersection and rock failure. TANG et al [18] developed the rock failure process analysis (RFPA) method and proposed a flow-stress-damage (FSD) coupling model for heterogeneous rocks, which solved the solution of discontinuity problems such as rock fracture process. Based on the RFPA method, LI et al [19] studied the influence of natural fracture on complex hydraulic fracture network, and concluded that hydraulic fracture is easier to propagate between the brittle minerals. In the later period, SHI [20] put forward the numerical simulation analysis method of discontinuous medium for the first time, which mainly includes the extended finite element method (X-FEM), 3D distinct element code (3DEC), peridynamics (PD) and particle flow code (PFC) [21-24]. The PFC method can not only simulate the heterogeneity and anisotropy of materials, but can also intuitively track the crack initiation and propagation process. Some scholars have studied the induction of hydraulic fractures by natural fractures based on PFC, and revealed the main control factors of the formation of complex fracture network and the fracture mode of the rock mass, which provides certain theoretical guidances for the on-site permeability enhancement technology of reservoir rock mass [25, 26].

In general, there are more researches on the hydraulic fracturing test and numerical simulation for coal and shale, but less for limestone. Besides, the hydraulic fracturing process of fractured rock mass under the comprehensive action of many factors is seldom considered by the previous researchers. In this paper, the limestone is taken as the fracturing object, and the fracturing results are analyzed in detail combined with the pump pressure curve, AE positioning, and fracture expansion. Further research is carried out based on PFC, and the fracture mode and hydraulic fracture propagation law of the rock mass under the comprehensive action of multiple factors are clarified, which has certain reference value for the further study of the hydraulic fracture mechanism of limestone.

2 Design and implementation of hydraulic fracturing test scheme

2.1 Test scheme design

To explore the influence mechanism of the principal stress difference and the water injection displacement on the crack growth pattern and fracturing pressure of limestone, the vertical well hydraulic fracturing test of limestone with the saturated sample triaxial fracturing device of Northeastern University of China was carried out. The device adopts true triaxial loading mode with the range of three-way pressure of 0-10 MPa, and the water pressure is loaded with a constant flow rate in the range of flow rate of 0-10 mL/min. The change curve of water pressure in the injection hole with time can be recorded accurately in realtime through the computer control system, and thus the information of fracturing pressure and fracture time can be obtained. The schematic diagram is shown in Figure 1.

The orthogonal test method is adopted for the design scheme, and the specific test scheme parameter settings are shown in Table 1. Among them, the working condition 5 adopts a variable displacement hydraulic pressure loading method. In this table, σ_v is the vertical stress; σ_H is the maximum horizontal stress; σ_h is the minimum horizontal stress; and σ_H-σ_h is the principal stress difference.

To accurately locate the three-dimensional space of the hydraulic fracture, the 16-channel AE monitoring system produced by the American Physical Acoustic Corporation (PAC) is used. In order to realize the three-dimensional spatial positioning of hydraulic fractures, 8 acoustic emission sensors are used in this test, which are arranged in such a way that two probes are installed along the diagonal of each side surface. The resonance frequency is 300 kHz, and the highest sampling rate is 10 MSPS, which greatly reduces the difference between the collected waveform and the real waveform. The specific monitoring parameters are shown in Table 2.

2.2 Preparation of hydraulic fracturing sample

The limestone block for fracturing is taken out from the ground and cut into a cube with a side length of 300 mm. A circular hole with a depth of 165 mm and a diameter of 25 mm is drilled vertically in the center of the rock upper surface. A steel pipe with an inner diameter of 15 mm, an outer diameter of 20 mm and a length of 140 mm is used to simulate the wellbore. The wellbore and the hole wall are bonded with the epoxy resin glue, and a 25 mm open-hole section is reserved at the bottom as the fracturing section. The prepared rock sample and geometric structure are shown in Figure 2.

First of all, the sealed rock sample is put into the triaxial fracturing chamber and the Vaseline is applied to make the AE probes closely adhere to the sample. Before the test, small displacement liquid injection shall be conducted before the test. When the pump pressure curve rises, it shows that the sealing effect is good. According to the test scheme, the triaxial confining pressure and the flow parameters of the advection pump are loaded to the specified value. Next, the pump pressure loading system is started to inject water into the central hole at a constant flow rate, and the water pressure information and the AE data are monitored and collected in realtime. Finally, when the water pressure drops suddenly and does not rise again in a few minutes, and the red fracturing fluid flows out at the bottom of the device, indicating that the hydraulic fracture has penetrated the whole sample. At this time, the fracturing is finished, experimenters stop the pump and discharge the fracturing fluid.

3 Test results and analysis

3.1 Hydraulic fracturing curve and AE energy analysis

Figure 3 shows the hydraulic pressure change curve and AE energy change histogram of the limestone during fracturing (Conditions 4 and 1 are only different in fracture pressure and fracture time, which have been shown in Table 3 and will not be shown in Figure 3). It can be seen from the figure that the entire fracturing process can be roughly divided into three stages: In the water injection stage (stage I), the change range of water pressure is very small, and there is almost no AE energy. After the water injection hole is filled with the fracturing fluid, the water pressure increases rapidly with the continuous injection of water, which is the pressure holding stage (stage II), and the sample has not yet cracked in this stage. Subsequently, the water pressure continues to increase and reach a peak value, which is the fracturing pressure of the rock mass. At this time (stage III), the open-hole section starts to crack. Due to the brittleness of the rock mass, the hydraulic fracture expands rapidly, and the water pressure drops sharply due to stress release.

Figure 1 Schematic diagram of saturated sample triaxial fracturing device (the black area is the pump pressure loading system, the blue area is the AE monitoring device, and the red area is the confining pressure loading system)

Table 1 Hydraulic fracturing test scheme

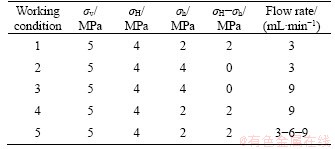
Table 2 AE monitoring parameters

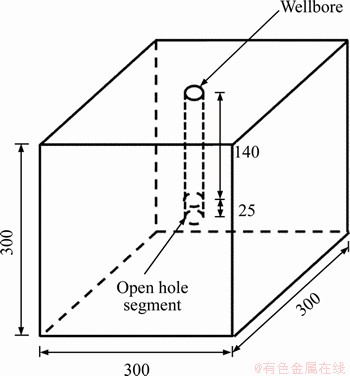
Figure 2 Hydraulic fracturing sample and geometric diagram (unit: mm)

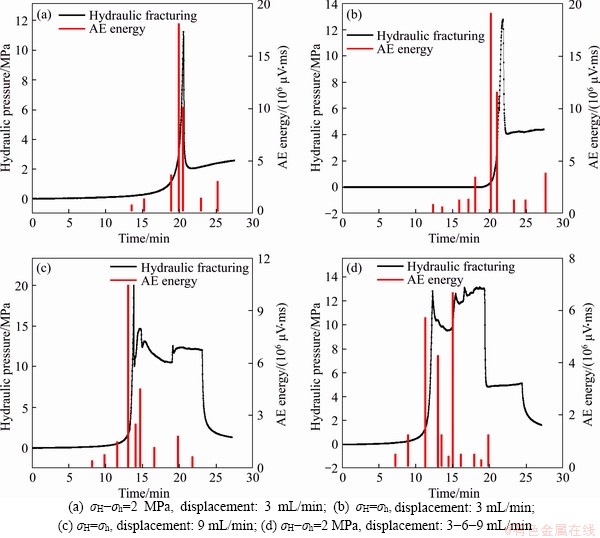
Figure 3 Water pressure curve and AE energy histogram:

Table 3 Fracture pressure and fracture time statistics of limestone hydraulic fracturing

Besides, the water injection displacement has a large effect on the change of water pressure in the crack propagation stage (stage III). Under the condition of low displacement, the principal stress difference has little effect on the propagation of hydraulic fracture, and the fracture mode of rock mass is splitting failure with a single fracture. After fracturing, the pumped water pressure and the filtered water pressure reach a dynamic equilibrium and the water pressure remains constant (Figures 3(a) and (b)). Under the high displacement, the water pressure has a secondary peak value, but it is less than the first fracturing pressure (Figure 3(c)), indicating that the main fracture is easier to communicate with the natural joint fracture to form a secondary fracture under the high displacement. After the second fracturing, the pump pressure jumps up and down in a zigzag shape near 11 MPa with an amplitude of about 1 MPa. This is mainly due to the formation and expansion of secondary fractures, which caused the internal frictional resistance of the fracture change.

Variable displacement water injection is used in condition 4, where 3 mL/min constant flow water injection is used in stage I, and then the displacement is increased to 6 mL/min until the rock mass breaks (stage III). At this time, the displacement increases to 9 mL/min, and the water pressure increases rapidly again. After several small fluctuations, it reaches the second peak value, and the peak stress is slightly greater than the first fracturing pressure, as shown in Figure 3(d). Therefore, when the variable displacement is loaded, it is easier to connect the natural fractures to form a complex fracture network, so the variable displacement fracturing is more conducive to improve the effect of deep reservoir fracturing.

It can also be seen from Figure 3 that the AE energy value has a good correspondence with the change of water pressure. When the water pressure reaches the peak value, the AE energy value reaches the maximum value correspondingly, and the energy change is the strongest during the crack growth stage. After reaching the fracturing pressure, the energy value drops rapidly, and the AE energy will fluctuate slightly, which is mainly due to the micro signal generated by the change of friction resistance between the fractures. Besides, for limestone samples, the AE energy is generally about 1.7-2 μV·ms at low displacement and 7-10 μV·ms at high displacement.

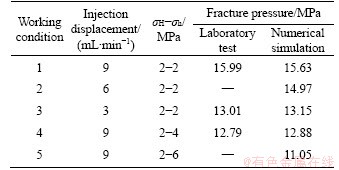
It can be seen from Table 3 that under the same water injection displacement, when σ_v, σ_H remain unchanged, with the increase of σ_h, the principal stress difference decreases, but the fracturing pressure increases, indicating that greater water pressure is needed to achieve fracturing under the condition of low principal stress difference. However, in the case of the same principal stress difference, with the increase of water injection displacement, the fracture time is shortened, which indicates that the fracture of limestone is easier to be realized under the condition of high displacement. Meanwhile, the fracturing pressures increase from 13.01 to 15.99 MPa, meaning that the fracturing pressure has a positive correlation with water injection displacement. Besides, when the variable displacement loading is used, the fracturing pressure is greater than that of single injection displacement, indicating that variable displacement loading is more likely to induce multi-point initiation and form a complex fracture network.

3.2 Analysis of fracture propagation law in limestone hydraulic fracturing

Through the surface observation and sectioning of the samples after fracturing, the hydraulic fractures can be roughly divided into two types: the single vertical fractures along the wellbore direction and the transverse-longitudinal crossed fractures. The following describes the two types of fractures in combination with the crack propagation patterns of rock samples under different conditions.

3.2.1 Single vertical fracture

Taking sample 1 as an example, as shown in Figure 4, the selected original rock is dense and brittle failure occurred after fracturing the sample. Only a vertical main fracture that has not yet penetrated the upper, and the lower bottom surfaces is generated on the right side. The fracture is relatively straight, and the fracturing fluid flows out of it. After sectioning, it can be observed that the fracturing of the sample is only completed in the right half of the wellbore, and the red fracturing fluid only covers the dotted line area in Figure 4. The fracture surface is relatively flat and extends along the direction of the maximum principal stress, which is consistent with the law of hydraulic fracture propagation under high principal stress difference.

Figure 5 shows the AE event location map and spectrum analysis of AE waveform. It can be seen from Figure 5(a) that the events monitored by AE are mainly concentrated in the open hole section when the pump pressure reaches the fracturing pressure, and the event points monitored during the fracturing process are mainly distributed in an elliptical area perpendicular to the wellbore, which is in good agreement with the fracture propagation mode observed after sectioning. The serial numbers represent the position of AE probes. As shown in Figure 5(b), in the initial stage of fracturing, the amplitude of AE waveform is very small. At the moment of sample fracturing, the amplitude rises abruptly, and the peak value is about 0.018 mV. After fracturing, the amplitude recovers to calm again. Based on the short-time Fourier transform, the spectrum analysis of AE waveform in the fracture stage is carried out, as shown in Figure 5(c). The frequency range of 250-300 kHz is highlighted, indicating that the energy in this area is very concentrated, which is the approximate distribution range of the main frequency of the limestone block.

Figure 4 Single vertical crack pattern of sample 1 (the red dotted line is the main fracture surface)

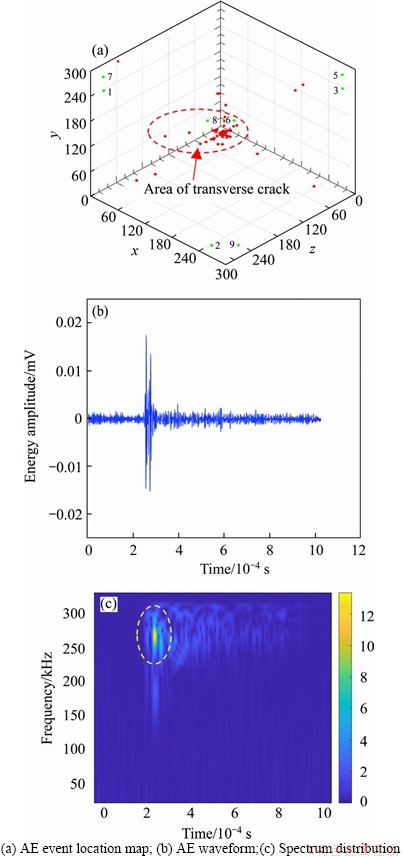
Figure 5 AE event location and spectrum analysis of AE waveform:

3.2.2 Transverse-longitudinal crossed fractures

Taking sample 3 as an example. As shown in Figure 6, after fracturing, there are several hydraulic fractures on the surface of the sample. σ_v is the vertical direction; σ_H and σ_h are the two main horizontal directions. The main fractures 1 and 3 are the longitudinal fractures, which expand along the axis of the wellbore but do not penetrate the upper and lower surfaces. The main fractures 2 is located near the wellbore and perpendicular to it, which is a transverse fracture. The distribution of hydraulic fracture after sectioning is shown in Figure 6. The hydraulic fractures cracked and extended from the open-hole section of the wellbore and finally penetrated the bottom and right boundary of the rock sample. In the process of expansion, the main fracture surface expands in a three-dimensional curved surface and the hydraulic fractures break and penetrate the natural joint, thereby forming a relatively complex fracture shape. Therefore, when the principal stress difference is small, it is easier to connect the natural fractures to form complex transverse-longitudinal crossed fractures by using high displacement fracturing.

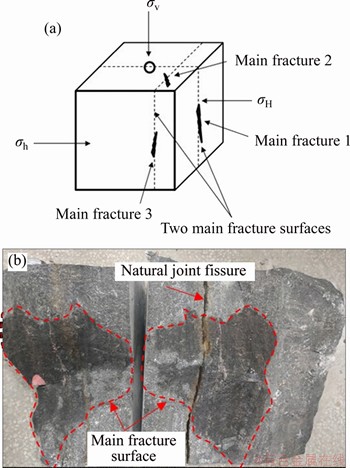
Figure 6 Distribution and expansion form of main fracture surface

From the AE positioning information in Figure 7(a), it can be seen that the AE events are concentrated in two nearly vertical elliptical areas, which is in good agreement with the shape of the fracture propagation surface. Besides, the amplitude of AE waveform is about 0.02 mV, which is greater than that when a single vertical fracture is generated, as shown in Figure 7(b). Meanwhile, it can be seen from Figure 7(c) that the spectrum is highlighted in the range of 230-280 kHz. Combined with Figure 5(c), the main frequency of limestone is maintained in the range of 230-300 kHz.

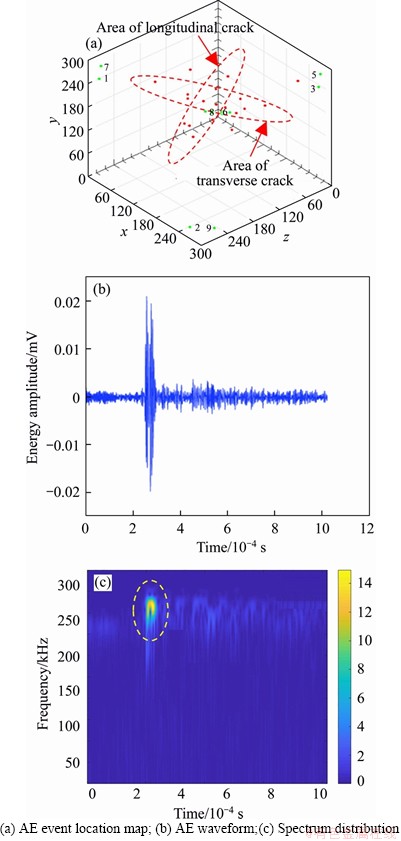
Figure 7 AE event location and spectrum analysis of AE waveform:

4 Discrete element simulation of hydraulic fracturing of limestone

4.1 Selection of micromechanical parameters

The correct selection of micro-parameters is the key to numerical analysis. To ensure the accuracy of the numerical model, the Brazilian splitting test, uniaxial and triaxial compression tests are first carried out for the original limestone, and the conventional mechanical parameters of the limestone are obtained, as shown in Table 4. Based on PFC2D software, the numerical models of 50 mm×100 mm and Φ50 mm is established, and the minimum radius R_min is 0.8 mm and the maximum radius R_max is 1.2 mm, and the flat-jointed model is used to simulate the bond between particles. The basic mechanical tests such as uniaxial compression and Brazilian splitting are carried out. Through constant parameter debugging, the final model failure mode and stress-strain curve are shown in Figure 8. It can be seen that the numerical simulation results of the model are in good agreement with the test results. Finally, the micromechanical parameters are shown in Table 5.

4.2 Establishment and verification of hydraulic fracturing model

4.2.1 Establishment of hydraulic fracturing model

The dimensions of the model are 300 mm× 300 mm. The uniform distribution is adopted for the filling of particles, and the minimum radius R_min is 0.8 mm and the maximum radius R_max is 1.2 mm. The pore diameter of water injection is 25 mm, and 18164 particles are generated in the end. The micro- parameters of the particles and contact bonding are shown in Table 5. The vertical and horizontal stresses are applied to the model through the servo control of the walls. Finally, the numerical calculation model is shown in Figure 9(a). To realize the simulation of hydraulic fracturing, this paper realizes the two-way coupling of fluid and solid based on the “pipe-domain” model in PFC [27], as shown in Figure 9(b).

4.2.2 Calibration of fluid parameters

The selection of reasonable fluid parameters is the key to the correctness of the hydraulic fracturing model. To ensure the accuracy of the model, the flow parameters are calibrated based on the test results of condition 1. Through the servo walls, 4 and 2 MPa stresses are applied to the vertical and horizontal boundaries of the model, respectively. And the water is injected at a constant rate of 3 mL/min until the cracks penetrate the entire model.

The crack propagation mode and the stress around the hole are shown in Figure 10. As shown in Figure 10(a), the hydraulic fractures propagate along the direction of the maximum principal stress and pass through the model boundary under the high principal stress difference. Figure 10(b) shows the horizontal, vertical, and tangential stress of the particles around the water injection hole. At 15600 steps, the hydraulic fracture penetrates the model; at this time, σ_x=11.2 MPa, σ_y=10.6 MPa, τ_xy=-0.7 MPa. According to the stress state at one point, the stress around the injection hole is 11.66 MPa, while the rock fracturing pressure obtained from the laboratory test is 11.48 MPa, indicating that the numerical simulation results are in good agreement with the test results. Finally, the model flow parameters are shown in Table 6.

Table 6 Fluid parameters of model

Table 4 Conventional physical and mechanical parameters of limestone

Figure 8 Comparison of indoor test and numerical simulation results:

Table 5 Micro contact parameters of particles

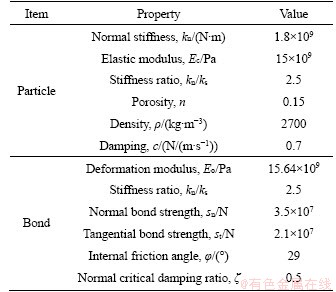
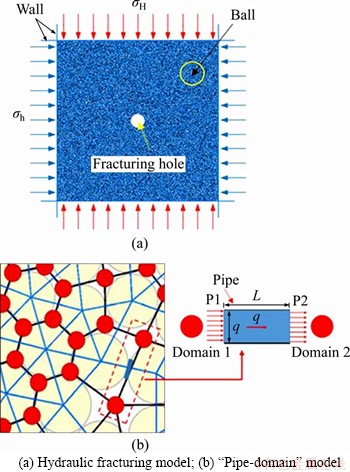
Figure 9 Numerical model of hydraulic fracturing:(red circle represents “domain”; black solid line represents “pipe”; blue solid line represents parallel bonding; and yellow circle represents particles)

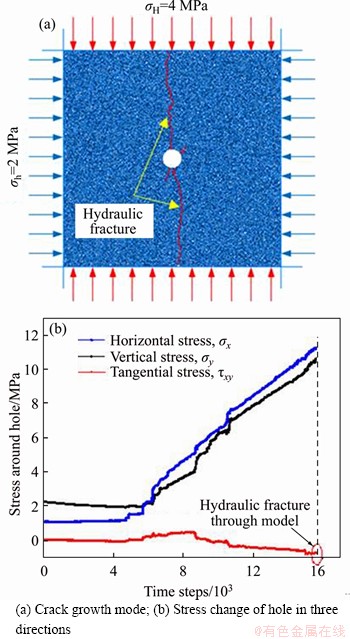
Figure 10 Numerical simulation results of condition 1:

4.2.3 Numerical simulation verification

Based on the micromechanical parameters and seepage parameters obtained above, the hydraulic fracturing simulation of rock mass under different water injection displacement and principal stress difference is carried out. Figure 11(a) shows the fracturing stress curve of rock mass under different water injection displacements when the principal stress difference is 0. Figure 11(b) shows the fracturing stress curve under different principal stress difference when the water injection displacement is 9 mL/min. It can be seen from Figure 11 that the fracturing pressure increases with the increase of the injection displacement and decreases with the increase of the maximum horizontal principal stress, and the larger the displacement and the principal stress difference are, the shorter the fracture time is, which is consistent with the conclusion of the test. The comparison between the simulation and the test results of fracturing stress is shown in Table 7. It can be seen from Table 7 that the fracturing pressure obtained from the simulation is in good agreement with the test results, which indicates that the numerical model built in this paper can well simulate the hydraulic fracturing of limestone.

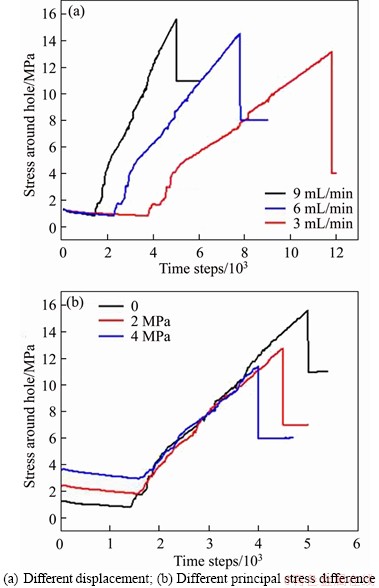
Figure 11 Stress change curve around hole:

Table 7 Comparison of numerical simulation and laboratory test results

4.3 Hydraulic fracturing simulation of fractured limestone

Due to the existence of bedding, cleavage, and other joint fissures in the limestone under the geological action, and to improve the energy production rate in the field hydraulic fracturing construction, directional perforation fracturing is often used [28, 29]. Therefore, based on the mesoscopic contact parameters and fluid parameters obtained above, a limestone model with a single horizontal joint fracture is established, as shown in Figure 12. The failure mode of joint rock mass and the propagation law of hydraulic fracture under the combined action of different perforation angles and principal stress difference are studied.

The perforations angles (θ) of 0, 30°, 45° and 60° are prefabricated at the injection hole, respectively, and the principal stress difference is set as 0, 2 and 6 through the walls. A total of 12 sets of numerical simulations are carried out. The specific design scheme is shown in Table 8, and the crack growth modes of each condition are shown in Figure 13.

Figure 12 Hydraulic fracturing model of fractured limestone with perforating

It can be seen from the crack propagation mode that when the principal stress difference is 0, the hydraulic crack propagates along the perforation direction at a low injection angle (0°≤θ≤30°), and the natural fracture has little influence on it; when θ=45°, a branch fracture perpendicular to the perforation direction is produced and captured by the natural fracture in the end; when θ=60°, the hydraulic fracture propagates along the perforation direction and is captured by the natural fracture subsequently, but finally passes through the model from the end of the natural fracture.

Table 8 Design scheme of numerical simulation

When the principal stress difference is 2 MPa and the injection angle θ≤45°, the main fracture expands along the perforation direction and a branch fracture perpendicular to the perforation direction is produced, forming a T-type fracture. According to Figures 13(a) and (b), when θ=60°, it can be seen that with the increase of the principal stress difference, the hydraulic fracture passes through the natural fracture and continues to expand along the direction of the maximum principal stress, indicating that the capture effect of the natural fracture on the hydraulic fracture is less than the induction effect of the principal stress difference.

Under high principal stress difference, the failure mode of the rock mass is tensile failure along the direction of the maximum principal stress. Under the low injection angle (0°≤θ≤30°), the main fracture propagates perpendicular to the perforation direction and passes through the natural fracture, while the branch fracture propagates along the direction of perforation and is finally captured by the natural fracture, and finally a X-type fracture is formed. However, the main crack propagates along the perforation angle at high injection angles (θ>45°). Due to the stress difference, the crack shifts to the direction of the maximum principal stress. In addition, compared with Figures 13(a)-(c), it can be seen that when the injection angle θ is 45°, the natural crack is more likely to induce branch crack and eventually be captured by it, and the T-shaped crack is formed in the end.

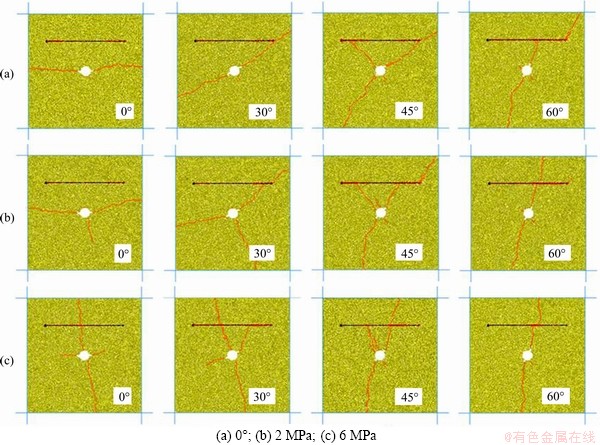
Figure 13 Crack propagation modes under different perforation angles with pricipal stress differences:(black horizontal line is natural fracture, and red curve represents hydraulic fracture)

Figure 14 shows the change curves of fracturing stress and the cumulative number of the cracks when fracturing with different perforation angles under the same principle stress difference. It can be seen from Figure 14(a) that when the principal stress difference is 0, the fracturing stress of rock mass increases first and then decreases with the increase of perforation angle; and when θ=45°,the fracturing stress reaches the peak value. Therefore, a low perforation angle is more conducive to fracture when the principal stress is 0. On the other hand, when σ_H-σ_h>0, the fracturing stress of rock mass increases significantly and decreases with the increase of perforation angle. When θ=0°, the fracturing stress is the largest, indicating that the fracturing is the most difficult when the perforation angle is perpendicular to the direction of the maximum principal stress under the high principal stress difference. Besides, when θ=60°, the principal stress difference has little effect on the fracture stress, which indicates that when the perforation angle is inclined to the direction of the maximum principal stress, the difference of principal stress has little effect on the fracture pressure.

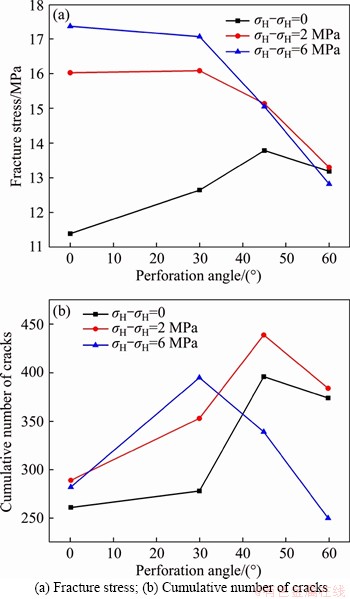
Figure 14 Fracture stress and cumulative number of cracks in rock with different perforation angles:

The cumulative number of cracks can represent the degree of fracture of the rock mass and the complexity of the cracks. From Figure 14(b), it can be seen that the cumulative number of cracks generally increases first and then decreases. At low principal stress difference, the number of cracks reaches the peak value when θ=45°, while the perforation angle is 30° under high principal stress difference. This is mainly because the perforation angle plays a decisive role in the propagation of the main fracture under the low principal stress difference. When θ=45°, it is easy to produce the T-type fracture that connects with the natural fracture. However, the propagation mode of hydraulic cracks under high principal stress difference is controlled by the direction of maximum principal stress and perforation angle. When θ=30°, the principal stress control is dominant and X-type cracks are generated.

5 Conclusions

In this paper, based on true triaxial hydraulic fracturing test and discrete element method (DEM) numerical simulation, the crack propagation mode and fracture pressure variation law of limestone under different working conditions are studied. The following conclusions are drawn:

1) The displacement has the greatest influence on the fracture propagation stage. A single through fracture is easy to form at low displacement, and the fracturing pressure is small. However, the fracturing pressure is higher at high displacement, and it is easier to induce branch fractures expansion to form secondary fracturing. Complex network fracture is easy to form during variable displacement fracturing, which is more conducive to improving the fracturing effect of the reservoir.

2) The AE event location map and energy amplitude can directly reflect the propagation mode of hydraulic fractures and the process of rock fracture. From the energy amplitude map and the main fracture surface after sectioning, there are two main types of fracture propagation modes of limestone during fracturing: the single vertical fracture and the transverse-longitudinal crossed complex fractures. When the principal stress difference is 0, it is easy to produce multi-point crack, and then transverse-longitudinal crossed complex fractures are generated, and the main fracture surface is a three-dimensional curved surface. Under the high principal stress difference, a single vertical crack is easy to form and expands along the direction of the maximum principal stress.

3) When the principal stress difference is 0, a low perforation angle is more conducive for fracturing. Meanwhile, under the high principal stress difference, when the perforation direction is inclined to the direction of the maximum principal stress, it is more conducive to realize the fracturing of rock mass. In addition, when the perforation angle θ>45°, the principal stress difference has little effect on the fracture pressure.

4) From the view of hydraulic fracture propagation morphology, the perforation angle plays a decisive role in the propagation of the main fracture under low principal stress difference. When θ=45°, the natural crack is more likely to induce branch crack and eventually be captured by it, and the T-shaped crack is formed in the end. However, the propagation mode of hydraulic cracks under high principal stress difference is controlled by the direction of the maximum principal stress and perforation angle. When θ≤30°, the principal stress control is dominant and X-type cracks are generated.

Contributors

The overarching research goals were developed by YANG Wei-min, ZHOU Zong-qing. LI Lian-chong, DING Ruo-song, GENG Yang and ZHAI Ming-yang carried out true triaxial hydraulic fracturing test. YANG Wei-min, DING Ruo-song and ZHAI Ming-yang analyzed the test results. GENG Yang and WU Zhong-hu established a numerical model. ZHOU Zong-qing and GENG Yang analyzed the calculated results. The initial draft of the manuscript was written by ZHOU Zong-qing and GENG Yang. All authors replied to reviewers’ comments and revised the final version.

Conflict of interest

YANG Wei-min, GENG Yang, ZHOU Zong-qing, LI Lian-chong, DING Ruo-song, WU Zhong-hu, and ZHAI Ming-yang declare that they have no conflict of interest.

References

[1] HU Wen-rui, WEI Yi, BAO Jing-wei. Development of the theory and technology for low permeability reservoirs in China [J]. Petroleum Exploration and Development (English version), 2018, 45(4): 685-697. DOI: 10.1016/S1876- 3804(18)30072-7.

[2] VANDENHOEK P J, VANDENBERG J T M, SHLYAPOBERSKY J. Theoretical and experimental investigation of rock dilatancy near the tip of a propagating hydraulic fracture [J]. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstracts, 1993, 30(7): 1261-1264. DOI: 10.1016/0148-9062(93) 90105-M.

[3] ZHANG De-cheng, RANJITH P G, PERERA M S A. The brittleness indices used in rock mechanics and their application in shale hydraulic fracturing: A review [J]. Journal of Petroleum Science & Engineering, 2016, 143: 158-170. DOI: 10.1016/j.petrol. 2016.02.011.

[4] PAN Dong-dong, LI Shu-cai, XU Zhen-hao, LI Li-ping, LU Wei, LIN Peng, HUANG Xin, SUN Shang-qu, GAO Cheng-lu. Model tests and numerical analysis for water inrush caused by karst caves filled with confined water in tunnels [J]. Chinese Journal of Geotechnical Engineering, 2018, 40(5): 828-836. DOI: 10.11779/CJGE201805007.

[5] LIU Hong-lei, YANG Tian-hong, CHEN Shi-kuo, YU Qing-lei, WANG Pei-tao. The mechanism of hydraulic fracturing and the engineering meaning of water outburst during rockmass failure [J]. Journal of Mining & Safety Engineering, 2010, 27(3): 356-362.

[6] NAOI M, CHEN You-qing, NISHIHARA K, YAMAMOTO K, YANO S, WATANABE S. Monitoring hydraulically- induced fractures in the laboratory using acoustic emissions and the fluorescent method [J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 104: 53-63. DOI: 10.1016/j.ijrmms.2018.02.015.

[7] WU Chen, GONG Feng-qiang, LUO Yong. A new quantitative method to identify the crack damage stress of rock using AE detection parameters [J]. Bulletin of Engineering Geology and Environment, 2020. DOI: 10.1007/s10064-020-01932-6.

[8] LI Zhi, JIA Chang-gui, YANG Chun-he, ZENG Yi-jin, GUO Yin-tong, HENG Shuai, WANG Lei, HOU Zhen-kun. Propagation of hydraulic fissures and bedding planes in hydraulic fracturing of shale [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(1): 12-20. DOI: 10.13722/j.cnki.jrme.2015.01.002. (in Chinese)

[9] WANG Han-yi. Hydraulic fracture propagation in naturally fractured reservoirs: Complex fracture or fracture networks [J]. Journal of Natural Gas Science and Engineering, 2019, 68: 102911. DOI: 10.1016/j.jngse.2019.102911.

[10] ZHAO Yu, HE Peng-fei, ZHANG Yong-fa, WANG Chao-lin. A new criterion for a toughness-dominated hydraulic fracture crossing a natural frictional interface [J]. Rock Mechanics & Rock Engineering, 2018. 52(8): 2617-2229. DOI: 10.1007/s00603-018-1683-y.

[11] GUO Tian-kui, ZHANG Shi-cheng, QU Zhan-qing, ZHOU Tong, XIAO Yong-shun, GAO Jun. Experimental study of hydraulic fracturing for shale by stimulated reservoir volume [J]. Fuel, 2014, 128: 373-380. DOI: 10.1016/j.fuel.2014.03. 029.

[12] MA Geng, ZHANG Fan, LIU Xiao, FENG Dan, ZHANG Peng-wei. Experimental study of impact of crustal stress on fracturing pressure and hydraulic fracture [J]. Rock and Soil Mechanics, 2016, 37(S2): 216-222. DOI: 10.16285/j.rsm. 2016.S2.026.

[13] WU Jing-jing, ZHANG Shao-he, SUN Ping-he, CAO Han, CHEN Jiang-zhan. Experimental study on acoustic emission characteristics in coal seam pulse hydraulic fracturing [J]. Journal of Central South University (Science and Technology), 2017, 48(7): 1866-1874. DOI: 10.11817/j.issn. 1672-7207.2017.07.025. (in Chinese)

[14] FAN Yong, ZHAO Yan-lin, ZHU Zhe-ming, ZHOU Chang-lin, ZHANG Xian-shang. Theoretical study of break down pressures and fracture initiation angles based on model containing wellbore and perforations [J]. Journal of Central South University (Science and Technology), 2019, 50(3): 669-678. DOI: 10.11817/j.issn.1672-7207.2019.03.021. (in Chinese)

[15] RUEDA C J A, MEJIA S E C, ROEHL D, PEREIRA L C. Hydro-mechanical modeling of hydraulic fracture propagation and its interactions with frictional natural fractures [J]. Computers and Geotechnics, 2019, 111: 290-300. DOI: 10.1016/ j.compgeo.2019.03.020.

[16] LIN Hai, DENG Jin-gen, LIU Wei, XIE Tao, XU Jie, LIU Hai-long. Numerical simulation of hydraulic fracture propagation in weakly consolidated sandstone reservoirs [J]. Journal of Central South University, 2018, 25(12): 2944-2952. DOI: 10.1007/s11771-018-3964-8.

[17] PAKZAD R, WANG S Y, SLOAN S W. Numerical simulation of hydraulic fracturing in low-/high-permeability, quasi-brittle and heterogeneous rocks [J]. Rock Mechanics & Rock Engineering, 2018, 51(4): 1153-1171. DOI: 10.1007/ s00603-017-1386-9.

[18] TANG Chen-an, THAM L G, LEE P K K, YANG Tian-hong. Coupled analysis of flow, stress and damage (FSD) in rock failure [J]. International Journal of Rock Mechanics & Mining Sciences, 2002, 39(4): 477-489. DOI: 10.1016/ S1365-1609 (02)00023-0.

[19] LI Zhi-chao, LI Lian-chong, LI Ming, ZHANG Liao-yuan, TANG Chun-an. A numerical investigation on the effects of rock brittleness on the hydraulic fractures in the shale reservoir [J]. Journal of Natural Gas Science & Engineering, 2017, 50: 22-32. DOI: 10.1016/j.jngse.2017.09.013.

[20] SHI Gen-hua. Discontinuous deformation analysis: A new numerical model for the statics and dynamics of deformable block structures [J]. Engineering Computations, 1992, 9(2): 157-168. DOI: 10.1108 /eb023855.

[21] VAHAB M, KHALILI N. Numerical investigation of the flow regimes through hydraulic fractures using the X-FEM technique [J]. Engineering Fracture Mechanics, 2016, 169: 146-162. DOI: 10.1016/j.engfracmech.2016.11.017.

[22] FARZIN H, ALI M. A new three dimensional approach to numerically model hydraulic fracturing process [J]. Journal of Petroleum Science and Engineering, 2014, 124: 451-467. DOI: 10.1016/ j.petrol.2013.12.006.

[23] GAO Cheng-lu, ZHOU Zong-qing, LI Zhuo-hui, LI Li-ping, CHENG Shuai. Peridynamics simulation of surrounding rock damage characteristics during tunnel excavation [J]. Tunnelling and Underground Space Technology, 2020, 97. DOI: 10.1016/j.tust. 2020.103289.

[24] ZHOU Zong-qing, RANJITH P G, YANG Wei-min, SHI Shao-shuai, WEI Che-che, LI Zhuo-hui. A new set of scaling relationships for DEM-CFD simulations of fluid–solid coupling problems in saturated and cohesiveless granular soils [J]. Computational Particle Mechanics, 2019, 6(4): 657-669. DOI: 10.1007/s40571-019-00246-z.

[25] WANG Tao, HU Wan-rui, ELSWORTH D, ZHOU Wei, ZHOU Wei-bo, ZHAO Xian-yu. The effect of natural fractures on hydraulic fracturing propagation in coal seams [J]. Journal of Petroleum Science & Engineering, 2017, 150: 180-190. DOI: 10.1016/j.petrol.2016.12.009.

[26] YOON J S, ZANG A, STEPHANSSON O, HOFMANN H, ZIMMERMANN G. Discrete element modelling of hydraulic fracture propagation and dynamic interaction with natural fractures in hard rock [J]. Procedia Engineering, 2017, 191: 1023-1031. DOI: 10.1016/j.proeng.2017. 05.275.

[27] Itasca Consulting Group Inc. PFC2D-particle flow code in two dimensions [M]. Ver. 4.0 User’s Manual. ICG, Minneapolis.

[28] GUO Tian-kui, QU Zhan-qing, GONG Di-guang, LEI Xin, LIU Ming. Numerical simulation of directional propagation of hydraulic fracture guided by vertical multi-radial boreholes [J]. Journal of Natural Gas Science and Engineering, 2016, 35: 175-188. DOI: 10.1016/j.jngse.2016. 08.056.

[29] CHENG Yu-gang, LU Yi-yu, GE Zhao-long, CHENG Liang, ZHENG Jing-wei, ZHANG Wen-feng. Experimental study on crack propagation control and mechanism analysis of directional hydraulic fracturing [J]. Fuel, 2018, 218: 316-324. DOI: 10.1016/j.fuel.2018.01.034.

(Edited by ZHENG Yu-tong)

中文导读

灰岩真三轴水力压裂试验和数值模拟

摘要：水力压裂作为深部能源开发的关键技术，促进了现代石油工业的快速发展。为研究垂直井水力压裂裂缝扩展机制和岩石破坏模式，开展了真三轴水力压裂试验和数值模拟研究，分析了主应力差、注水排量、射孔角度和天然裂缝对水力裂缝扩展的影响。结果表明，灰岩裂缝扩展模式主要分为两类：单一垂直裂缝和纵横向交叉复杂裂缝。高排量下岩体的破裂压力更大，且易诱发二次压裂；而变排量加载更容易诱发形成裂缝网络。同时，灰岩在压裂过程中的声发射波形幅值在0.01～0.02 mV范围内，主频保持在230～300 kHz范围内。当射孔角度θ=45°时，易产生与天然裂缝交汇的“T”型水力裂缝，而当θ=30°时，易产生X型裂缝。研究结果可为进一步研究灰岩水力压裂机理提供参考。

关键词：真三轴；水力压裂；声发射(AE)；PFC；射孔角度；天然裂缝

Foundation item: Projects(51879148, 51709159, 51911530214) supported by the National Natural Science Foundation of China; Project(2019GSF111030) supported by Shandong Provincial Key R&D Program of China; Project(KT201804) supported by the Project of Special Fund for Science and Technology of Water Resources Department of Guizhou Province, China

Received date: 2020-06-09; Accepted date: 2020-08-31

Corresponding author: ZHOU Zong-qing, PhD, Associate Professor; Tel: +86-18363077928; E-mail: Zongqing.Zhou@sdu.edu.cn; ORCID: https://orcid.org/0000-0003-4418-1264