
ARTICLE
J. Cent. South Univ. (2019) 26: 1250-1259
DOI: https://doi.org/10.1007/s11771-019-4084-9
Numerical simulation for Darcy-Forchheimer 3D rotating flow subject to binary chemical reaction and Arrhenius activation energy
Tasawar HAYAT1, 2, Arsalan AZIZ1, Taseer MUHAMMAD3, Ahmed ALSAEDI2
1. Department of Mathematics, Quaid-I-Azam University, Islamabad 44000, Pakistan;
2. Nonlinear Analysis and Applied Mathematics (NAAM) Research Group, Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia;
3. Department of Mathematics, Government College Women University, Sialkot 51310, Pakistan
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: Three-dimensional Darcy-Forchheimer nanoliquid flow in the presence of rotating frame and activation energy is inspected. Flow is developed through linearly stretching of the surface. Convection of heat and mass exchange is given due consideration. The novel characteristics in regards to Brownian dispersion and thermophoresis are retained. The variation in partial differential framework (PDEs) to nonlinear ordinary differential framework (ODEs) is done through reasonable transformations. Governing differential frameworks have been computed in edge of NDSolve. Discussion regarding thermal field and concentration distribution for several involved parameters is pivotal part. Physical amounts like surface drag coefficients, transfer of heat and mass rates are portrayed by numeric esteems. It is noticed that impacts of porosity parameter and Forchheimer number on the thermal and concentration fields are quite similar. Both temperature and associated thermal layer thickness are enhanced for larger porosity parameter and Forchheimer number. Temperature and concentration fields exhibit similar trend for the higher values of rotational parameter. Effects of thermal and concentration Biot numbers on the temperature and concentration fields are qualitatively similar. Higher Prandtl and Schmidt numbers correspond to stronger temperature and concentration fields. Larger nondimensional activation energy, temperature difference parameter and fitted rate constant yield weaker concentration field. Brownian motion parameter for temperature and concentration has reverse effects while similar trend is observed via thermophoresis parameter.
Key words: nanoparticles; rotating frame; Arrhenius activation energy; Darcy-Forchheimer porous space; numerical solution
Cite this article as: Tasawar HAYAT, Arsalan AZIZ, Taseer MUHAMMAD, Ahmed ALSAEDI. Numerical simulation for Darcy-Forchheimer 3D rotating flow subject to binary chemical reaction and Arrhenius activation energy [J]. Journal of Central South University, 2019, 26(5): 1250–1259. DOI: https://doi.org/10.1007/s11771-019-4084-9.
1 Introduction
Nanofluid is a colloidal blend acquired by nanoparticles of size under 100 nm out of a working fluid. Fundamentally working fluids accommodate lower thermal exchange highlights on account of their weak warm proficiency. In this way, the expansion of nanoparticles in such sort of working liquids known as nanofluids is very appealing strategy to upgrade heat productivity of such fluids. Advance nanofluid has an essential job for cooling rate prerequisites with high warm proficiency. Directly nanofluid elements have increased astounding consideration of researchers because of their bewitching warm transport in a few down to earth zones. Today the nanofluids applications are effectively experienced in the enterprises. The utilization of nanofluids incorporates however no restricted to warm exchangers, impingement planes, car, sustainable power sources, warming and treating process, atomic reactors, electronic chips cooling, grease, ignition and drug and so forth. CHOI et al [1] discussed the structure of nanomaterials. They deduced that addition of nanoparticles in the basic working fluids is exceedingly helpful to increase cooling capacity of normal fluids. BUONGIORNO [2] created two-part connection for heat vitality transport in nanoliquids. Connection depends on two-critical slips to be specific Brownian development and thermophoresis. Some ongoing looks into on nanofluid stream can be seen through attempts [3–15].
Concentration contrast of species exists in blend with mass exchange wonder changing convergence of species in blend move from higher concentration locale to lower concentration district. The minimum mandatory vitality that is needed by reactants previously occurring synthetic response is characterized as enactment vitality. Mass exchange process alongside synthetic response with initiation vitality by and large discovers applications in mechanics of oil and water emulsions, compound designing, nourishment handling and so on. Right off the bat the normal convection stream of parallel blend in a permeable space with activation energy is studied by BESTMAN [16]. Temperamental regular convection stream with nth-arrange reaction and activation energy was explored by MAKINDE et al [17]. Further recent attempts on activation energy can be seen through the studies [18–23].
Enthusiasm of recent specialists in warmth exchange through permeable space is helpful for applications in innovative, compound and assembling forms. Unequivocal procedures toward this path may incorporate unrefined petroleum creation, the plan of atomic reactors, atomic based archives, use of geothermal essentialness, development of dampness in sinewy protection, substance synergist reactors, sun based power, units of the vitality stockpiling and a few others. Darcy’s law expresses that there exists an immediate connection between volumetric motion of liquid through medium and weight slope. Essentially, articulation of DARCY [24] is utilized generally in the writing for issues related to demonstrating and investigation of stream soaking permeable space. Customary Darcy's law is appropriate just for low velocity and littler porosity. Such law dismisses idleness and limit impacts. Changed type of traditional Darcy’s hypothesis results in non- Darcian permeable medium which joins boundary and inertial impacts. Uniqueness in porosity and high stream rates occur in numerous pragmatic conditions. Idea of such state can't be imagined because of insuitability of Darcy's law. For high velocity, flow enters a nonlinear flow locale and therefore inactivity can’t be overlooked. Subsequently FORCHHEIMER [25] employed latency through consideration of square speed term in energy articulation. MUSKAT [26] named this commitment as Forchheimer factor. The examinations on Darcy-Forchheimer stream can be cited through the investigations [27–33] and different endeavors in that.
Heat move in rotating streams is very alluring. It is a result of their tremendous applications in assembling of precious stone development, PC stockpiling gadget, warm power age and gas turbine rotors and so on. WANG [34] figured out explanatory answers for gooey liquid stream by an extended sheet in turning outline. TAKHAR et al [35] tended to be magnetohydrodynamic in pivoting extended stream. JAVED et al [36] built nearby comparative answers for pivoting stream by exponential twisting surface. ZAIMI et al [37] examined visco-elastic liquid stream in turning outline. ROSALI et al [38] investigated turning stream by exponential porous surface. MUSTAFA et al [39] talked about Maxwell liquid stream subject to variable warm conductivity and pivoting outline. Three-dimensional turning Maxwell nanoliquid stream was broke down by HAYAT et al [40]. MUSTAFA et al [41] registered diagnostic answers for pivoting stream of Oldroyd-B fluid.
HAYAT et al [42] discussed Darcy- Forchheimer flow of nanofluid subject to rotating frame. Very recently HAYAT et al [43] computed numerical solutions of Darcy-Forchheimer three- dimensional rotating flow of nanofluid with prescribed heat and mass flux conditions.
Fundamental point of current article is to address Darcy-Forchheimer 3D pivoting stream of nanoliquid initiated by straightly deformable sheet with concoction response and actuation vitality. Brownian development and thermophoresis instruments are investigated. Convective states of warmth and mass are examined. NDsolve system is actualized for arrangements. Charts portraying critical parts of present investigation are shown and dissected. In addition, surface drag coefficients and warmth and mass exchange rates are registered and examined.
2 Statement
Three-dimensional nanoliquid stretched flow in a rotating frame is analyzed. Chemical reaction subject to concept of activation energy is examined. Darcy-Forchheimer relation for porous medium is studied. Nanoliquid has qualities of Brownian development and thermophoresis. Sheet is warmed by hot fluid with temperature Tf and concentration Cf. Heat and mass transport coefficients are taken h1 and h2. Surface in Cartesian facilitate framework is agreed with xy-plane and fluid involves z≥0. Liquid rotates reliably about z-axis subject to constant angular velocity ω (see Figure 1). Governing boundary layer expressions are as follows:
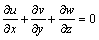 (1)
(1)
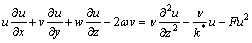 (2)
(2)
 (3)
(3)
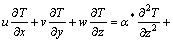
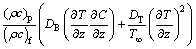 (4)
(4)

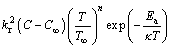 (5)
(5)
with the following conditions:
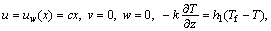
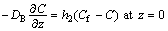 (6)
(6)
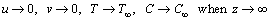 (7)
(7)
where (u, v, w) stand for velocities in x-, y- and z-directions, v(=μ/ρf) for kinematic viscosity, μ for dynamic viscosity, k for thermal conductivity, ρf for density, k* for permeability of porous space, F=Cb/(xk*1/2) for variable inertial coefficient of porous space, α*=k/(ρc)f for thermal diffusivity, (ρc)p for effective heat potential of nanomaterial, (ρc)f for heat potential of the liquid, T for temperature, DB for Brownian diffusivity, C for concentration, DT for thermophoretic diffusivity, Cb for drag coefficient, kr for reaction rate, n for fitted rate constant, Ea for activation energy, κ for Boltzmann constant, h1 for heat transfer coefficient, h2 for mass transfer coefficient, C∞ for ambient concentration and T∞ for ambient temperature. Setting
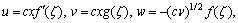
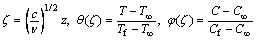 (8)
(8)
expression (1) is automatically verified and Eqs. (2)–(7) are reduced to
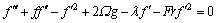 (9)
(9)
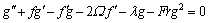 (10)
(10)
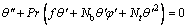 (11)
(11)
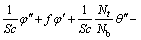
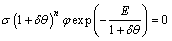 (12)
(12)

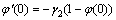 (13)
(13)
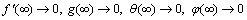 (14)
(14)
Here porosity parameter, Forchheimer number, rotation parameter, Schmidt number, Prandtl number, chemical reaction parameter, Brownian movement parameter, thermal Biot number, thermophoresis parameter, nondimensional activation energy, temperature difference parameter and concentration Biot number are symbolized by λ, Fr, Ω, Sc, Pr, σ, Nb, γ1, Nt, E, δ and γ2 respectively. These nondimensional parameters are expressed by
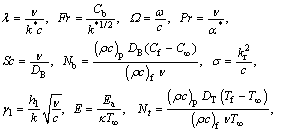
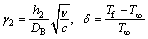 (15)
(15)
The physical quantities are given by [44]
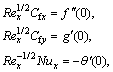
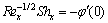 (16)
(16)
In above expressions 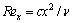 represents the local Reynolds number.
represents the local Reynolds number.

Figure 1 Flow configuration
3 Graphical outcomes and discussion
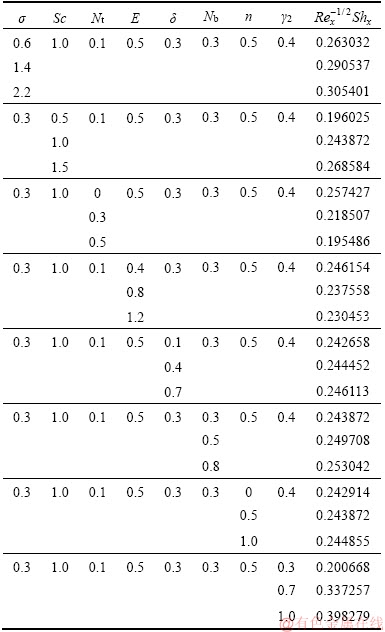
This segment investigates effects of couple of relevant physical flow variables like thermal Biot parameter γ1, Prandtl parameter Pr, temperature difference parameter δ, porosity parameter λ, concentration Biot parameter γ2, Brownian movement parameter Nb, nondimensional activation energy E, Forchheimer number Fr, nondimensional reaction rate σ, Schmidt parameter Sc, thermophoresis number Nt, fitted rate constant n and rotational parameter Ω on nondimensional temperature θ(ζ) and concentration φ(ζ). Figure 2 presents curves of temperature field θ(ζ) for higher λ. It has been seen that by expanding λ, entrance profundity of θ(ζ) lifts. Physically, the presence of permeable space creates opposition in smooth movement and extreme, indicating diminishing in liquid velocity. Consequently an addition is seen for temperature and relating layer thickness. Influence of Forchheimer number Fr on temperature θ has been shown in Figure 3. Temperature and layer thickness are expanding elements of Fr. Figure 4 shows temperature θ(ζ) for particular data of rotational parameter. Biggerm Ω prompts an improvement in temperature. Figure 5 shows effect of heat Biot parameter γ1 on temperature. Here an expansion in γ1 causes stronger temperature.Figure 6 presents estimations θ(ζ) as for Pr. Temperature is diminished through Pr. Prandtl number has turn around relationship with thermal diffusivity. Bigger Prandtl parameter incites poor thermal diffusivity. Varieties in temperature θ(ζ) for thermophoresis variable Nt are shown in Figure 7. Truth be told, bigger thermophoresis number prompts more temperature and related layer thickness. An extension in Nt causes update in thermophoresis diffusion. This keeps in expanding temperature. Figure 8 is depicted to consider variety in temperature θ(ζ) affected by Brownian development parameter Nb. An augmentation in Nb causes an improvement in θ(ζ). Physically, the unsystematic development of nanoparticles ascends by upgrading Nb because crash of particles happens. Subsequently active vitality is changed over into thermal vitality which prompts an augmentation in temperature and related layer. Figure 9 portrays that bigger porosity parameter λ displays an expansion in concentration φ(ζ). Figure 10 shows effect of Fr on concentration φ(ζ). Both concentration and related layer are expanded by means of Fr.Figure 11 displays variety in φ(ζ) for changing Ω. It is seen that by growing turn parameter, an enhancement is seen in concentration φ and its relating layer. Figure 12 depicts effect of concentration Biot parameter γ2 on concentration φ. Concentration and related layer are more for γ2. Figure 13 presents impact of nondimensional activation energy E on concentration φ(ζ). Here an augmentation in E rots adjusted Arrhenius work. This in the end builds up the generative synthetic response because concentration φ(ζ) upgrades. Figure 14 displays that an improvement in nondimensional reaction rate σ shows a rot in concentration. Figure 15 illustrates impact of temperature difference parameter δ on φ(ζ). Here φ(ζ) is noted diminishing capacity of δ. Figure 16 presents concentration φ(ζ) for evolving n. It is seen that by enhancing n, entrance profundity of φ(ζ) finishes to more slender. Figure 17 shows impact of Sc on concentration φ. This figure demonstrates that bigger Sc rots concentration φ(ζ). Schmidt number includes Brownian development. An extension in Sc prompts poor Brownian development, which shows a reduction in concentration and layer thickness. Figure 18 displays concentration φ(ζ) for specific estimations of thermophoresis number Nt. Plainly higher Nt offers ascent to more concentration φ(ζ) and layer thickness. Figure 19 illustrates that concentration φ(ζ) lessens for Nb. Table 1 shows surface drag coefficients for a few estimations of λ, Fr and Ω. Drag coefficients delineate expanding pattern for higher Ω while reverse effect is watched for bigger λ and Fr. Table 2 is prepared to validate present data with previously published data by JAVED et al [36]. Here we analyzed that the present solutions have good agreement with previous solutions by JAVED et al [36]. Table 3 lists local Nusselt number by means of λ, Fr, Ω, Nt, γ1, Nb and Pr. Heat exchange rate decays via λ, Fr, Ω, Nt and Nb. Effects of γ1 and Pr on heat transfer rate are very comparable. Table 4 indicates numerical data of mass exchange rate by means of σ, Sc, Nt, E, δ, Nb, n and γ2. Here we saw that mass transfer rate is higher and brings down qualities for bigger (Sc, δ, σ, Nb, n, γ2) and (E, Nt) respectively.
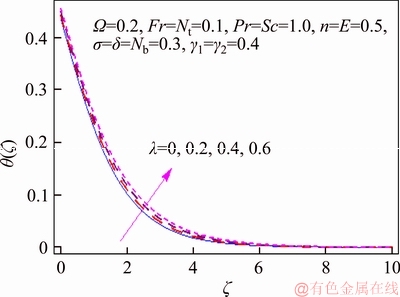
Figure 2 θ(ζ) variation for λ
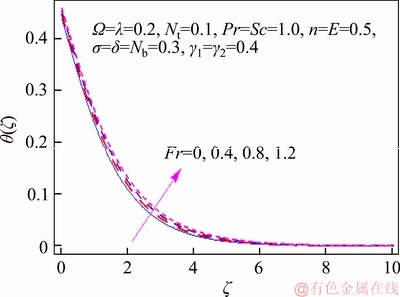
Figure 3 θ(ζ) variation for Fr
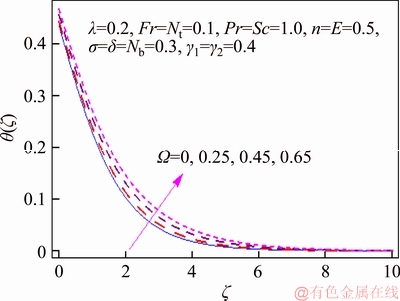
Figure 4 θ(ζ) variation for Ω
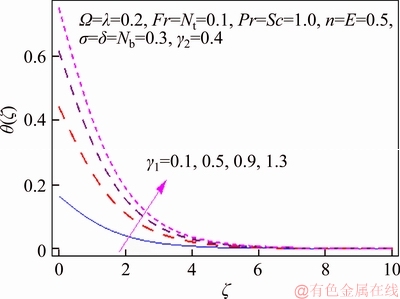
Figure 5 θ(ζ) variation for γ1
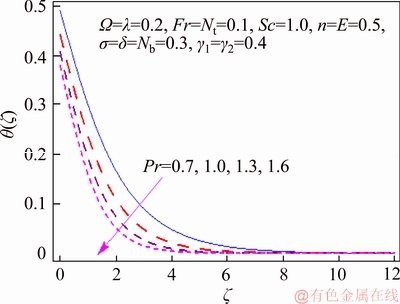
Figure 6 Plots of θ(ζ) for Pr

Figure 7 θ(ζ) variation for Nt
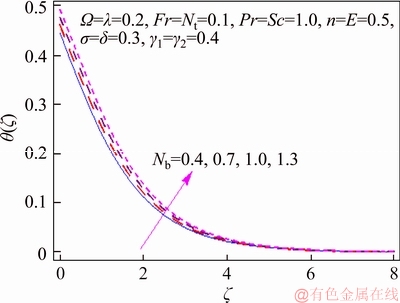
Figure 8 θ(ζ) variation for Nb
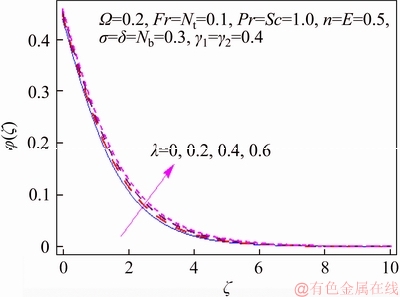
Figure 9 φ(ζ) variation for λ
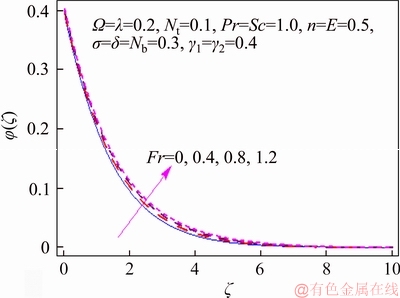
Figure 10 φ(ζ) variation for Fr
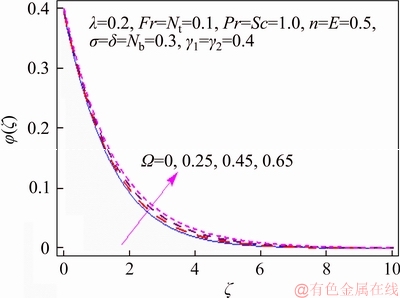
Figure 11 φ(ζ) variation for Ω
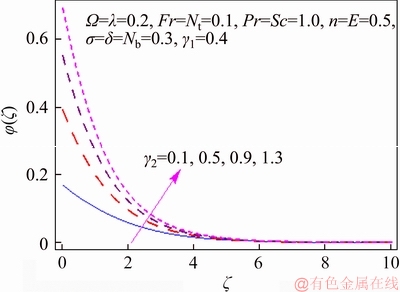
Figure 12 φ(ζ) variation for γ2
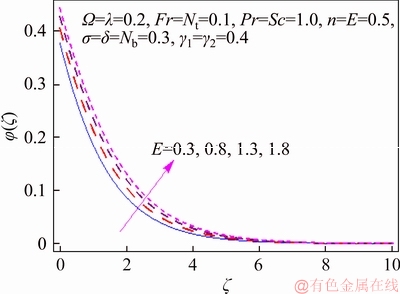
Figure 13 φ(ζ) variation for E

Figure 14 φ(ζ) variation for σ
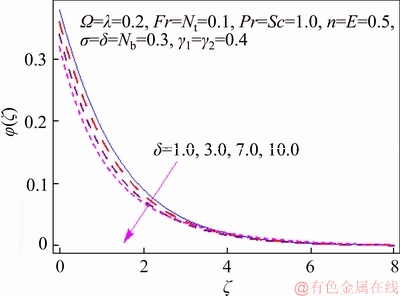
Figure 15 φ(ζ) variation for δ
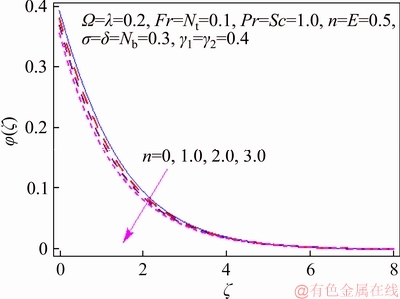
Figure 16 φ(ζ) variation for n
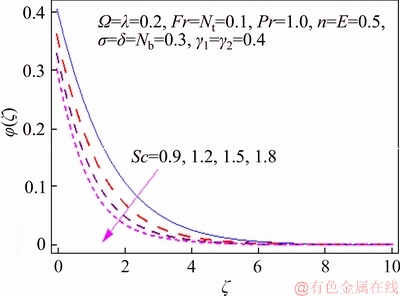
Figure 17 φ(ζ) variation for Sc
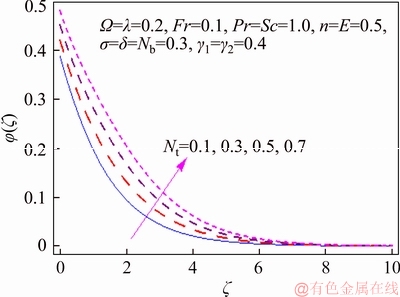
Figure 18 φ(ζ) variation for Nt
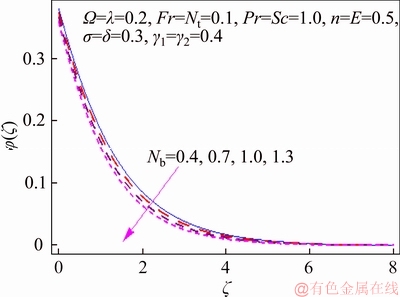
Figure 19 φ(ζ) variation for Nb
Table 1 Surface drag coefficients 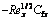 and
and 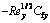 for varying Fr, λ and Ω
for varying Fr, λ and Ω
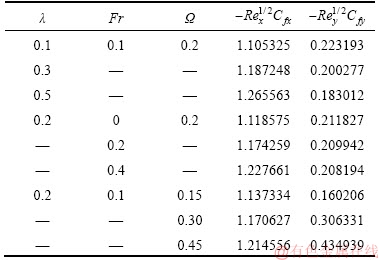
Table 2 Comparative data of –f ″(0) and –g′(0) for varying Ω when λ=Fr=0
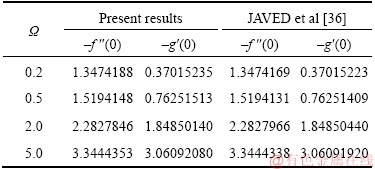
Table 3 Heat transfer rate 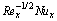 for varying λ, Fr, Ω, Nt, γ1, Nb and Pr
for varying λ, Fr, Ω, Nt, γ1, Nb and Pr
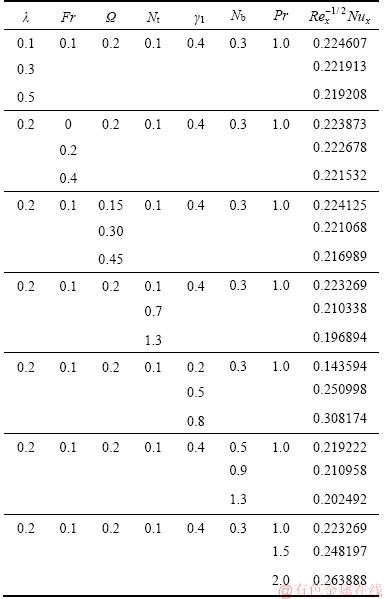
Table 4 Mass transfer rate 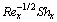 for varying σ, Sc, Nt, E, δ, Nb, n and γ2
for varying σ, Sc, Nt, E, δ, Nb, n and γ2
4 Conclusions
Effect of activation energy in convective Darcy-Forchheimer flow is studied. Major results of present study can be noted below:
1) Temperature and concentration have similar qualitative effects for λ and Fr.
2) Through rotation Ω, there is an enhancement of temperature θ(ζ) and concentration φ(ζ).
3) Heat and mass Biot numbers give rise to temperature and concentration.
4) Larger activation energy E shows higher concentration field φ(ζ).
5) Bigger Prandtl Pr and Schmidt Sc numbers lead to weaker temperature θ(ζ) and concentration φ(ζ).
6) Effects of δ and σ on concentration are qualitatively similar.
7) Brownian parameter Nb for temperature and concentration has reverse effects.
8) Temperature and concentration have similar trend for Nt.
References
[1] CHOI S U S, EASTMAN J A. Enhancing thermal conductivity of fluids with nanoparticles [C]// ASME International Mechanical Engineering Congress & Exposition. San Francisco: American Society of Mechanical Engineers, 1995.
[2] BUONGIORNO J. Convective transport in nanofluids [J]. ASME Journal of Heat Transfer, 2006, 128: 240–250.
[3] ZAIB A, BHATTACHARYY K, SHAFIE S. Unsteady boundary layer flow and heat transfer over an exponentially shrinking sheet with suction in a copper-water nanofluid [J]. Journal of Central South University, 2015, 22: 4856–4863.
[4] ASHRAF M B, HAYAT T, ALSAEDI A, SHEHZAD S A. Convective heat and mass transfer in MHD mixed convection flow of Jeffrey nanofluid over a radially stretching surface with thermal radiation [J]. Journal of Central South University, 2015, 22: 1114–1123.
[5] SHEHZAD S A, HUSSAIN T, HAYAT T, RAMZAN M, ALSAEDI A. Boundary layer flow of third grade nanofluid with Newtonian heating and viscous dissipation [J]. Journal of Central South University, 2015, 22: 360–367.
[6] HAYAT T, AZIZ A, MUHAMMAD T, AHMAD B. Influence of magnetic field in three-dimensional flow of couple stress nanofluid over a nonlinearly stretching surface with convective condition [J]. PloS One, 2015, 10: e0145332.
[7] SHEHZAD N, ZEESHAN A, ELLAHI R, VAFAI K. Convective heat transfer of nanofluid in a wavy channel: Buongiorno's mathematical model [J]. Journal of Molecular Liquids, 2016, 222: 446–455.
[8] HAYAT T, AZIZ A, MUHAMMAD T, ALSAEDI A. On magnetohydrodynamic three-dimensional flow of nanofluid over a convectively heated nonlinear stretching surface [J]. International Journal of Heat and Mass Transfer, 2016, 100: 566–572.
[9] HAYAT T, AZIZ A, MUHAMMAD T, ALSAEDI A. Numerical study for nanofluid flow due to a nonlinear curved stretching surface with convective heat and mass conditions [J]. Results in Physics, 2017, 7: 3100–3106.
[10] HSIAO K L. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature [J]. International Journal of Heat and Mass Transfer, 2017, 112: 983–990.
[11] HAYAT T, AZIZ A, MUHAMMAD T, ALSAEDI A. A revised model for Jeffrey nanofluid subject to convective condition and heat generation/absorption [J]. PloS One, 2017, 12: e0172518.
[12] SHEIKHOLESLAMI M. Influence of magnetic field on Al2O3–H2O nanofluid forced convection heat transfer in a porous lid driven cavity with hot sphere obstacle by means of LBM [J]. Journal of Molecular Liquids, 2018, 263: 472–488.
[13] AZIZ A, ALSAEDI A, MUHAMMAD T, HAYAT T. Numerical study for heat generation/absorption in flow of nanofluid by a rotating disk [J]. Results in Physics, 2018, 8: 785–792.
[14] SHEIKHOLESLAMI M, JAFARYAR M, LI Z. Second law analysis for nanofluid turbulent flow inside a circular duct in presence of twisted tape turbulators [J]. Journal of Molecular Liquids, 2018, 263: 489–500.
[15] HAYAT T, AZIZ A, MUHAMMAD T, ALSAEDI A. Numerical simulation for three-dimensional flow of Carreau nanofluid over a nonlinear stretching surface with convective heat and mass conditions [J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2019, 41: 55.
[16] BESTMAN A R. Natural convection boundary layer with suction and mass transfer in a porous medium [J]. International Journal of Energy Research, 1990, 14: 389–396.
[17] MAKINDE O D, OLANREWAJU P O, CHARLES W M. Unsteady convection with chemical reaction and radiative heat transfer past a flat porous plate moving through a binary mixture [J]. Africka Matematika, 2011, 22: 65–78.
[18] MALEQUE K A. Effects of exothermic/endothermic chemical reactions with Arrhenius activation energy on MHD free convection and mass transfer flow in presence of thermal radiation [J]. Journal of Thermodynamics, 2013, 2013: 692516.
[19] AWAD F G, MOTSA S, KHUMALO M. Heat and mass transfer in unsteady rotating fluid flow with binary chemical reaction and activation energy [J]. PloS One, 2014, 9: e107622.
[20] ABBAS Z, SHEIKH M, MOTSA S S. Numerical solution of binary chemical reaction on stagnation point flow of Casson fluid over a stretching/shrinking sheet with thermal radiation [J]. Energy, 2016, 95: 12–20.
[21] SHAFIQUE Z, MUSTAFA M, MUSHTAQ A. Boundary layer flow of Maxwell fluid in rotating frame with binary chemical reaction and activation energy [J]. Results in Physics, 2016, 6: 627–633.
[22] ANURADHA S, YEGAMMAI M. MHD radiative boundary layer flow of nanofluid past a vertical plate with effects of binary chemical reaction and activation energy [J]. Global Journal of Pure and Applied Mathematics, 2017, 13: 6377–6392.
[23] KHAN M I, QAYYUM S, HAYAT T, WAQAS M, KHAN M I, ALSAEDI A. Entropy generation minimization and binary chemical reaction with Arrhenius activation energy in MHD radiative flow of nanomaterial [J]. Journal of Molecular Liquids, 2018, 259: 274–283.
[24] DARCY H. Les Fontaines Publiques De La Ville De Dijon [M]. Paris: Victor Dalmont, 1856. (in French)
[25] FORCHHEIMER P. Wasserbewegung durch boden [J]. Zeitschrift des Vereins deutscher Ingenieure, 1901, 45: 1782–1788.
[26] MUSKAT M. The flow of homogeneous fluids through porous media[M]. Edwards, MI, 1946.
[27] PAL D, MONDAL H. Hydromagnetic convective diffusion of species in Darcy-Forchheimer porous medium with non-uniform heat source/sink and variable viscosity [J]. International Communications in Heat and Mass Transfer, 2012, 39: 913–917.
[28] BAKAR S A, ARIFIN N M, NAZAR R, ALI F M, POP I. Forced convection boundary layer stagnation-point flow in Darcy-Forchheimer porous medium past a shrinking sheet [J]. Frontiers in Heat Mass Transfer, 2016, 7: 38.
[29] UMAVATHI J C, OJJELA O, VAJRAVELU K. Numerical analysis of natural convective flow and heat transfer of nanofluids in a vertical rectangular duct using Darcy- Forchheimer-Brinkman model [J]. International Journal of Thermal Sciences, 2017, 111: 511–524.
[30] SHEIKHOLESLAMI M. Influence of Lorentz forces on nanofluid flow in a porous cavity by means of non-Darcy model [J]. Engineering Computations, 2017, 34: 2651–2667.
[31] HAYAT T, AZIZ A, MUHAMMAD T, ALSAEDI A. Darcy-Forchheimer three-dimensional flow of Williamson nanofluid over a convectively heated nonlinear stretching surface [J]. Communications in Theoretical Physics, 2017, 68: 387–394.
[32] HAYAT T, HAIDER F, MUHAMMAD T, ALSAEDI A. Darcy-Forchheimer squeezed flow of carbon nanotubes with thermal radiation [J]. Journal of Physics and Chemistry of Solids, 2018, 120: 79–86.
[33] HAYAT T, AZIZ A, MUHAMMAD T, ALSAEDI A. An optimal analysis for Darcy-Forchheimer 3D flow of Carreau nanofluid with convectively heated surface [J]. Results in Physics, 2018, 9: 598–608.
[34] WANG C Y. Stretching a surface in a rotating fluid [J]. Journal of Applied Mathematics and Physics, 1988, 39: 177–185.
[35] TAKHAR H S, CHAMKHA A J, NATH G. Flow and heat transfer on a stretching surface in a rotating fluid with a magnetic field [J]. International Journal of Thermal Sciences, 2003, 42: 23–31.
[36] JAVED T, SAJID M, ABBAS Z, ALI N. Non-similar solution for rotating flow over an exponentially stretching surface [J]. International Journal of Numerical Methods for Heat and Fluid Flow, 2011, 21: 903–908.
[37] ZAIMI K, ISHAK A, POP I. Stretching surface in rotating viscoelastic fluid [J]. Applied Mathematics and Mechanics (English Edition), 2013, 34: 945–952.
[38] ROSALI H, ISHAK A, NAZAR R, POP I. Rotating flow over an exponentially shrinking sheet with suction [J]. Journal of Molecular Liquids, 2015, 211: 965–969.
[39] MUSTAFA M, HAYAT T, ALSAEDI A. Rotating flow of Maxwell fluid with variable thermal conductivity: An application to non-Fourier heat flux theory [J]. International Journal of Heat and Mass Transfer, 2017, 106: 142–148.
[40] HAYAT T, MUHAMMAD T, MUSTAFA M, ALSAEDI A. An optimal study for three dimensional flow of Maxwell nanofluid subject to rotating frame [J]. Journal of Molecular Liquids, 2017, 229: 541–547.
[41] MUSTAFA M, HAYAT T, ALSAEDI A. Rotating flow of Oldroyd-B fluid over stretchable surface with Cattaneo- Christov heat flux: Analytic solutions [J]. International Journal of Numerical Methods for Heat and Fluid Flow, 2017, 27: 2207–2222.
[42] HAYAT T, AZIZ A, MUHAMMAD T, ALSAEDI A. Darcy-Forchheimer flow of nanofluid in a rotating frame [J]. International Journal of Numerical Methods for Heat and Fluid Flow, 2018, https://doi.org/10.1108/HFF-01-2018- 0021.
[43] HAYAT T, AZIZ A, MUHAMMAD T, ALSAEDI A. Numerical simulation for Darcy-Forchheimer three- dimensional rotating flow of nanofluid with prescribed heat and mass flux conditions [J]. Journal of Thermal Analysis and Calorometry, 2018, DOI: https://doi.org/10.1007/ s10973-018-7847-x.
[44] JAVED M, FAROOQ M, AHMAD S, ANJUM A. Melting heat transfer with radiative effects and homogeneous- heterogeneous reaction in thermally stratified stagnation flow embedded in porous medium [J]. Journal of Central South University, 2018, 25(11): 2701–2711. DOI: https://doi.org/ 10.1007/s11771-018-3947-9.
(Edited by YANG Hua)
中文导读
基于二元化学反应和Arrhenius活化能的Darcy-Forchheimer流体三维旋转数值模拟
摘要:研究了旋转框架和活化能存在下的三维Darcy-Forchheimer纳米流动。考虑了热对流和质量交换,保留了布朗色散和热泳的新特征。通过合理的变换实现了偏微分系统(PDES)向非线性常微分系统(ODES)的转换。选择NDSolve的边界条件,计算了控制差分方程。重点讨论了几个相关参数下的热场和浓度分布。用数值来描述表面阻力系数、热量传递和质量交换率等物理量。结果表明,孔隙度和Forchheimer数对热场和浓度场的影响是相似的。随着孔隙度的增大和Forchheimer数的增加,温度升高和相应的热层厚度增大。温度场和浓度场随着旋转角的增大而呈现相似的变化趋势。热和浓度Biot数对温度场和浓度场的影响在本质上是相似的。较高的Prandtl和Schmidt数对应较强的温度场和浓度场。较大的无量纲活化能、温差和拟合速率常数对应较弱的浓度场。布朗运动参数对温度和浓度的作用是相反的,而热泳参数的作用是相似的。
关键词:纳米粒子;旋转框架;Arrhenius活化能;Darcy-Forchheimer 多孔空间;数值解
Received date: 2018-09-03; Accepted date: 2018-11-29
Corresponding author: Arsalan AZIZ, PhD Candidate; Tel: +92-332-0332048; E-mail: arsalan_qau@yahoo.com; ORCID: 0000-0002- 1985-7392