J. Cent. South Univ. Technol. (2011) 18: 1554-1562

DOI: 10.1007/s11771-011-0872-6

Synchronous tracking control of 6-DOF hydraulic parallel manipulator using cascade control method

PI Yang-jun(皮阳军)^{1, 2}, WANG Xuan-yin(王宣银)¹, GU Xi(顾曦)¹

1. State Key Laboratory of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027, China;

2. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: The synchronous tracking control problem of a hydraulic parallel manipulator with six degrees of freedom (DOF) is complicated since the inclusion of hydraulic elements increases the order of the system. To solve this problem, cascade control method with an inner/outer-loop control structure is used, which masks the hydraulic dynamics with the inner-loop so that the designed controller takes into account of both the mechanical dynamics and the hydraulic dynamics of the manipulator. Furthermore, a cross-coupling control approach is introduced to the synchronous tracking control of the manipulator. The position synchronization error is developed by considering motion synchronization between each actuator joint and its adjacent ones based on the synchronous goal. Then, with the feedback of both position error and synchronization error, the tracking is proven to guarantee that both the position errors and synchronization errors asymptotically converge to zero. Moreover, the effectiveness of the proposed approach is verified by the experimental results performed with a 6-DOF hydraulic parallel manipulator.

Key words: synchronization error; cross-coupling; cascade control; hydraulic dynamics; parallel manipulator; degree of freedom

1 Introduction

Parallel manipulator is a closed-loop kinematic chain mechanism whose end-effector is linked to the base by several independent kinematic chains [1]. It has been widely used in various industrial applications, such as construction and mining industries, as well as motion simulators, due to its distinct advantages of fast response speed, high system stiffness, and high specific force [2-3]. The kinematics and dynamics of parallel manipulator have been extensively studied, while high performance controllers of parallel manipulator need further investigations, as higher tracking precision has been increasingly demanded in various industrial applications [4-5].

In general, the control strategies for parallel manipulator can be largely divided into two schemes: task space control and joint space control [6]. The task space control scheme is based on the dynamics described by the task space. However, this control scheme needs the information from a 6-DOF sensor to obtain the pose and the displacement of the moving platform. Otherwise, it requires direct kinematics or other methods to estimate the pose and displacement of the moving platform [7].  The joint space control scheme is designed to make the actual actuator lengths conform to the desired lengths which are obtained by using the inverse kinematics. The joint space control scheme is much simpler for the control design, as it can be implemented as a collection of multiple, independent single-input single-output (SISO) control systems [6]. However, the control loop of an individual joint receives only the local feedback information, but no feedback from other joints. The most of existed control approaches of parallel manipulator did not consider the synchronization among control loops [8]. If one joint encounters disturbances, the others do not respond. The lack of synchronization will lead to large coupling errors which degrade the tracking performance of parallel manipulator.

In fact, parallel manipulator can be treated as a multiple-axe system with kinematical constraints [9]. It has been observed that axes must be synchronized with high-accuracy and high-speed motion tracking control of parallel manipulators. Crossing-coupling control provides a unique advantage and opportunity to solve the synchronized control problem posed by parallel manipulators [10]. Recently, crossing-coupling control is introduced to solve the position synchronization of multiple motion axes. SUN et al [5, 11] presented a method that utilizes the cross-coupling concept to solve the synchronous tracing control of planer parallel robot. ZHAO et al [8-9] developed a robust adaptive terminal sliding mode position synchronized control approach for the operation of multiple motion axe systems. However, the above controllers are designed for electrically driven systems. It cannot be directly used here as the parallel manipulator driven by hydraulic actuators in this study.

Hydraulic actuators have many distinct advantages, such as the ability to produce large forces at high speeds, high durability and stiffness, and rapid response [12-13]. However, hydraulic systems also have a number of characteristics which complicate the development of high-performance controllers. The dynamics of hydraulic systems is highly nonlinear due to the phenomena such as fluid compressibility, nonlinear servo valve flow-pressure characteristics, and dead band due to the internal leakage and hysteresis [13]. Unlike the electrical actuators that resemble force sources, hydraulic actuators resemble velocity sources [3-4]. Therefore, controllers that have been designed for manipulator control, assuming the capability of setting actuator force, cannot be used here. To solve this problem, cascade control method has been presented by SEPEHRI et al [14] and HEINTZE and VAN DER WEIDEN [15]. GUO et al [7] also presented a cascade position tracking controller to control a hydraulic parallel manipulator. However, it does not consider the synchronization among control loops. Cascade controller consists of two parts, namely the inner loop and the outer loop. Hydraulic dynamics is masked with the inner loop, and then the outer loop does not concern the hydraulic dynamics.

In this work, cascade control and crossing-coupling control methodology are integrated to solve the synchronous tracking control of a 6-DOF hydraulic parallel manipulator. Cascade control consists of an inner loop and an outer loop. Feedback linearization is adopted to compensate the hydraulic nonlinearity in the inner loop. It gives the hydraulic actuator the characteristic of force generator. The outer loop is designed to reject the external disturbances and make the moving platform track in a synchronous manner. The position synchronization errors are defined as differential position errors of all possible pairs of two neighbor joints. Joint position error and synchronization error are combined to construct the so-called coupled position error. The outer loop controller is developed with the feedback of this coupled position error. It is proved that both position and synchronization errors guarantee asymptotic convergence to zero by the outer loop controller.

The main differences between this work and Ref.[5] are: 1) Cascade control methodology is used here, so that this controller can be directly used in hydraulic parallel manipulator. 2) This controller does not have a sign function or saturation function. The forms of the control laws are different from those of Ref.[5].

2 Modeling

The 6-DOF hydraulic parallel manipulator consists of a base platform, a moving platform, six hydraulic actuators, and twelve universal joints. The moving platform and base platform are connected by the six hydraulic actuators, each of which has two universal joints. B_i and A_i (i=1, …, 6) are the coordinates of the universal joints of each platform. The base inertia coordinate is O_g-X_gY_gZ_g, and the moving coordinate is O_p-X_pY_pZ_p. The main structure parameters of the platform are: the radius of the base platform of R₀, the radius of the moving platform of R₁, the angles of two neighbor universal joints of each platform of θ₀ and θ₁, the length of the actuators of q and the initial height between the two center points of the platform of h₀ (see Fig.1). The detailed parameters of this parallel manipulator are given in Table 1.

2.1 Kinematics

The generalized coordinate vector, which describes the position and orientation of the moving platform, can be defined as  in the Cartesian space. The length vector of six actuators is given by q=

The direct position kinematics problem

is to determine the generalized coordinate vector of the platform, given the six actuator lengths. It is well known that the direct position kinematics of the 6-DOF parallel manipulator does not have a closed-form solution. However, it can be solved in a few milliseconds due to the development of digital technology development, though it relies on numerical methods. Inverse kinematics concerns the determination of the length vector of six actuators corresponding to a given generalized coordinate vector of moving platform. Considering the i-th actuator of the parallel manipulator (see Fig.1), the length vector of the i-th actuators can be denoted as

                                                            (1)

where 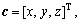 describes the position of the point O_p with respect to the base inertia coordinate. Vector b_i describes the position of the point B_i with respect to the moving coordinate. Vector a_i denotes the position of the point A_i with respect to the base inertia coordinate. R represents the rotation matrix. The detailed expressions for the rotation matrix can be found in Ref.[16].

Fig.1 Schematic diagram of 6-DOF parallel manipulator

Table 1 Parameters of hydraulic parallel manipulator

The length of an actuator can be computed by the Euclidean norm as

                                                                       (2)

2.2 Dynamics

The rigid body dynamics of 6-DOF parallel robot manipulator can be described as a second-order nonlinear differential equation, which is given by

                                                   (3)

where X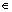R⁶, is a vector of the platform generalized coordinates, and F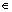R⁶, is the vector of the generalized applied force of the actuators. M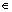R^6×6, is the robot mass matrix, V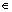R^6×6, contains Coriolis and centripetal terms, and G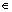R⁶, represents gravitational effects. J_f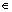R^6×6, is the force Jacobian matrix of the system. The detailed expressions for the above matrices can be found in Ref.[16].

3 Cascade control design

In general, the control of hydraulic manipulators is more challenging than that of their electrical counterparts. Hydraulic actuators cannot be modeled as a force or torque sources. Cascade controller consists of two parts, namely the inner loop and the outer loop. It masks the hydraulic dynamics with the inner loop, and then the outer loop does not concern the hydraulic dynamics. The control scheme is shown in Fig.2.

3.1 Inner loop design

The aim of the inner loop is to mask the hydraulic dynamics. In other words, it gives the hydraulic actuator the characteristic of a force generator. In the hydraulic parallel manipulator, hydraulic actuator is a typically valve-controlled single rod hydraulic system, as shown in Fig.3.

Taking leakage and compressibility into consideration, the dynamics of cylinder oil flow can be written as follows [17]:

                      (4)

                      (5)

where x_L is the displacement of the piston; β_e is the bulk modulus of the fluid; A₁ and A₂ are the areas of the two sides of the piston; P₁ and P₂ are the pressures inside the two chambers of the cylinder; C_t is the internal leakage coefficient; V₁ and V₂ are the total fluid volumes of the two sides of the cylinder, and given as

                                                       (6)

                                            (7)

L is the piston stroke; V₁₀ and V₂₀ are the initial fluid volumes of the two sides of the cylinder.

Q₁ and Q₂ are the fluid flow rates of the two chambers of the cylinder. They are related to the spool valve displacement of the servo valve x_v and given as

                       (8)

                     (9)

where P_s is the supply pressure, P_r is the pressure of oil tank, which is always zero, and k_q is the flow gain coefficient of the servo valve and given as

                                                           (10)

w is the servo valve area gradient, C_d is the discharge coefficient of cylinder and ρ is the oil density.

Fig.2 Controller implementation block diagram

Fig.3 Single-rod hydraulic servo system

In some literatures, the dynamics of servo valve has been incorporated in the controller design. Here, the valve dynamics is neglected and the servo valve opening x_v is proportional to the control input, since a high- response servo valve is used. Then x_v=k_au, where k_a is the servo amplifier gain and u is the servo valve control input signal.

Equations (4)-(10) depict the dynamics of the valve-controlled single-rod hydraulic servo system. The aim of inner loop control is to make the net force of the hydraulic fluid on the piston track the desired force.

The net force of the hydraulic fluid on the piston is given by

                                                           (11)

Differentiating the fluid force on the piston yields

                                                           (12)

After considering Eqs.(4)-(10), we have

                                                                 (13)

where

                                                (14)

                                (15)

Choose u as

                                                               (16)

where

                                                      (17)

and k is a positive force error gain.

Combining Eqs.(13) and (16) yields the following equation

                                                                 (18)

where

It shows that the force error e_F→0 with time constant λ=1/k:

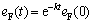                                                         (19)

Remark 1: The hydraulic actuator dynamics is masked in the inner loop. This inner loop controller gives the hydraulic actuator the characteristic of a force generator, where the net force of the hydraulic fluid on the piston F tracks the desired force F_d with first order dynamics.

Remark 2: In the inner loop, the length of hydraulic actuator x_L, the pressures of two chambers of hydraulic actuator, P₁ and P₂, can be measured by integrated transducers of parallel manipulator. The derivatives of above measured parameters are estimated by using the Matlab Simulink^TM.

3.2 Outer loop design

However, the expression of the desired force F_d in Eq.(17) is still unknown. The modeling error of hydraulic actuator which is used in inner loop control exists. Hence, the outer loop controller must be robust to handle the modeling error and other uncertainties. The outer loop controller is concerned with the tracking control of the moving platform and rejecting external disturbance of the system. There have been remarkable efforts using crossing-coupling control to improve the synchronization performance. Firstly, a synchronization error is defined to represent the coupling effects of the active actuators in the manipulator. Then, the controller is designed by combining the position error and the synchronization error.

3.2.1 Synchronization error

The essential feature that differentiates synchronized control from conventional control is the employment of an additional feedback signal termed as the synchronization error. The synchronization goal is motivated by the fact: if the ratio of the actual position/rotation of each actuator at each sampling time is equal to that of all other actuators, the 6-DOF hydraulic parallel manipulator moves in a synchronous manner [5, 18]. Thus, the synchronization goal is defined as

                      (20)

where q_i denotes the length of the i-th actuator, q_id denotes the desired length of the i-th actuator. To achieve this goal, the motion of each actuator and its two adjacent actuators must synchronize. A series of synchronization functions are given as

    (21)

The following equation can be derived from Eq.(21) by using Taylor expansion:

                              (22)

where   denotes higher order term, 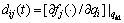 denotes a diagonal coupling parameter regarding the first-order error e_i(t). Note that d_ij(t) is bounded.

Base on Eqs.(20)-(22), the synchronization errors are defined as

               (23)

Rewrite the synchronization errors as

                                                           (24)

where

T is a constant gain matrix, and can be expressed as

                           (25)

where a_i=1/q_id.

Then, the control objective is to design the actuator control inputs to make e(t)→0 and ε(t)→0 as t→∞.

3.2.2 Outer loop control design

The coupled position error including the position error and the synchronization error of actuators is defined as

                                    (26)

where β is a positive constant. When the coupled position error  both position error and synchronization error converge to zero [5, 19].

According to the coupled position errors, the slide mode is defined as

                   (27)

where

and Λ is a positive constant.

Differentiating both sides of Eq.(27) with respect to time yields

                           (28)

Define the control law of outer loop controller (the desired force for inner loop controller) as

                            (29)

where K₁ is a positive constant, F_ip is the actuating force exerting on the platform by the i-th actuator, which can be calculated by Eq.(3).

To prove the stability of the proposed controller, a Lyapunov function V_i is defined as

                    (30)

where m_i denotes the mass of the piston of the i-th actuator. K₂ is a positive constant.

Differentiating both sides of Eq.(30) with respect to time yields

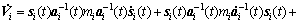
                (31)

Considering the forces balance equation for the asymmetric piston, there is

                                                           (32)

Substituting Eq.(29) into system dynamics Eq.(32) and using Eq.(28) yields the following equation:

                         (33)

Multiplying both sides of Eq.(33) with 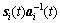 yields the following equation:

                                                (34)

Substituting Eq.(34) into Eq.(30) yields the following equation:

                                             (35)

From Eqs.(26) and (27), the following equations can be deduced:

                                                  (36)

Then, Eq.(35) can be written as

     (37)

From Eq.(37), we know that s_i(t) and ε_i(t) are bounded in terms of L₂ norm. Then,  and  are bounded from Eq.(27). Hence,  is bounded from differentiating Eq.(26).  is bounded from differentiating Eq.(24). From Eq.(33), we know that  is bounded. Therefore,  and  are uniformly continuous. From Barbalat’s lemma [18], s_i(t)→0 and ε_i(t)→0 as time t→∞.

Also, the Lyapunov function candidate satisfies

                                                              (38)

Therefore, the controller is proposed to guarantee the asymptotical convergence to zero of both the position errors and synchronization errors [19], i.e.  and  as time t→∞.

4 Experiments

The proposed controller was experimentally evaluated using a 6-DOF hydraulic parallel manipulator (see Fig.4). The parallel manipulator is driven by six single-rod hydraulic actuators from Moog Industrial Corporate. The integrated position transducer measures the position of the piston. Pressure sensors are installed in each chamber of the cylinders. Each cylinder is controlled by one servo valve (Moog J661-301) manufactured by Moog Industrial Corporate. The dynamics of the valve is ignored. The actual values of system parameters are given in Table 1.

The hardware configuration of the control system consists of two PC-compatible computers: a host and a target. The host and target PCs are directly connected using a cross-over unshielded twisted pair cable. All analog measurement signals (the cylinder position, the chamber pressures, the supplied pressure, and the load forces) are fed back to a target PC through four plugged-in DAQ cards. The four DAQ cards consist of two PCI1716Ls, a PCL812 and a PCL726 from the Advantech Company. To attenuate the influence of noise, all measured signals are processed through low-pass filters. The proposed controller is implemented on the target PC, which is independent of the host PC and must be booted using a special boot disc to load the Matlab xPC Target Real-time Kernel. The control frequency of 500 Hz is successfully achieved by using this setup.

To verify the effectiveness of the proposed control scheme, the comparative results of the experiments with the proposed synchronous controller and well-tuned PID controller are presented here. The control parameters of the proposed control scheme are given as β=diag{0.2}, Λ=diag{0.5}, K₁=diag{6}, K₂=diag{10}, and k=diag{20}.

The desired trajectory is defined as

                                               (39)

Figures 5 and 6 show the joint tracking errors of well-tuned PID controller and the proposed controller, respectively. Figures 7 and 8 show the task space tracking errors of well-tuned PID controller and the proposed controller, respectively. The maximum task space tracking errors are 6.6 mm and 2.2 mm for well- tuned PID controller and the proposed controller, respectively. The synchronization errors with the proposed controller are given in Fig.9. Figure 10 shows the force tracking errors of the inner loop controller of the proposed controller. From these experimental results,

Fig.4 Experimental setup

Fig.5 Joint tracking errors with well-tuned PID controller: (a) e₁; (b) e₂; (c) e₃; (d) e₄; (e) e₅; (f) e₆

Fig.6 Joint tracking errors with proposed controller: (a) e₁; (b) e₂; (c) e₃; (d) e₄; (e) e₅; (f) e₆

Fig.7 Task space tracking errors with well-tuned PID controller

Fig.8 Task space tracking errors with proposed controller

it is obviously shown that the proposed synchronous controller attains better tracking performances.

Fig.9 Synchronization errors with proposed controller: (a) ε₁;  (b) ε₂; (c) ε₃; (d) ε₄; (e) ε₅; (f) ε₆

Fig.10 Force tracking errors of the inner loop controller:     (a) Actuator 1; (b) Actuator 2; (c) Actuator 3; (d) Actuator 4;  (e) Actuator 5; (f) Actuator 6

5 Conclusions

1) The cross-coupling control approach and the cascade control approach are combined to address the synchronous tracking control problem of a 6-DOF hydraulic parallel manipulator.

2) The cascade control method is applied to separate the hydraulic dynamics from the mechanical part. The cross-coupling control approach utilizes the feedback of both the position error and the synchronization error, which are defined as differential position errors between two adjacent actuators. The proposed controller is proven to guarantee that both the position errors and the synchronization errors asymptotically converge to zero.

3) The experimental results performed with a hydraulic 6-DOF parallel manipulator demonstrate the effectiveness of the proposed approach.

References

[1] MERLET J P. Parallel robots [M]. Kluwer Academic Publishers, 2006: 9.

[2] DASGUPTA B, MRUTHYUNJAYA T S. The Stewart platform manipulator: A review [J]. Mechanism and Machine Theory, 2000, 35(1): 15-40.

[3] SIROUSPOUR M R, SALCUDEAN S E. Nonlinear control of hydraulic robots [J]. IEEE Transactions on Robotics and Automation, 2001, 17(2): 173-182.

[4] DAVLIAKOS I, PAPADOPOULOS E. Model-based control of a 6-dof electrohydraulic Stewart-Gough platform [J]. Mechanism and Machine Theory, 2008, 43(11): 1385-1400.

[5] SUN D, LU R, MILLS J K, WANG C. Synchronous tracking control of parallel manipulators using cross-coupling approach [J]. International Journal of Robotics Research, 2006, 25(11): 1137-1147.

[6] KIM H S, CHO Y M, LEE K I. Robust nonlinear task space control for 6 DOF parallel manipulator [J]. Automatica, 2005, 41(9): 1591-1600.

[7] GUO H B, LIU Y G, LIU G R, LI H R. Cascade control of a hydraulically driven 6-DOF parallel robot manipulator based on a sliding mode [J]. Control Engineering Practice, 2008, 16(9): 1055-1068.

[8] ZHAO D Y, LI S Y, GAO F. Fully adaptive feedforward feedback synchronized tracking control for Stewart Platform systems [J]. International Journal of Control Automation and Systems, 2008, 6(5): 689-701.

[9] ZHAO D, LI S, GAO F, ZHU Q. Robust adaptive terminal sliding mode-based synchronised position control for multiple motion axes systems [J]. IET Control Theory and Applications, 2009, 3(1): 136-150.

[10] KOREN Y. Cross-coupled biaxial computer control for manufacturing systems [J]. ASME Journal of Dynamic Systems, Measurement, and Control, 1980, 102(4): 265-272.

[11] SUN D. Position synchronization of multiple motion axes with adaptive coupling control [J]. Automatica, 2003, 39(6): 997-1005.

[12] GUAN C, PAN S X. Adaptive sliding mode control of electro-hydraulic system with nonlinear unknown parameters [J]. Control Engineering Practice, 2008, 16(11): 1275-1284.

[13] YAO B, BU F P, REEDY J, CHIU G T C. Adaptive robust motion control of single-rod hydraulic actuators: Theory and experiments [J]. IEEE/ASME Transactions on Mechatronics, 2000, 5(1): 79-91.

[14] SEPEHRI N, DUMONT G, LAWRENCE P, SASSANI F. Cascade Control of Hydraulically Actuated Manipulators [J]. Robotica, 1990, 8: 207-216.

[15] HEINTZE J, VAN DER WEIDEN A. Inner-loop design and analysis for hydraulic actuators, with an application to impedance control [J]. Control Engineering Practice, 1995, 3(9): 1323-1330.

[16] LI Q. Research on the low velocity movement of the electro-hydraulic 6DOF parallel platform [D]. Hangzhou: Zhejiang University, 2008. (in Chinese)

[17] MERRITT H. Hydraulic control systems [M]. Wiley, 1967.

[18] UN D, MILLS J. Adaptive synchronized control for coordination of multirobot assembly tasks [J]. IEEE Transactions on Robotics and Automation, 2002, 18(4): 498-510.

[19] SLOTINE J, LI W. Applied nonlinear control [M]. Prentice Hall, 1991: 40-154.

(Edited by YANG Bing)

Foundation item: Project(50375139) supported by the National Natural Science Foundation of China; Project(NCET-04-0545) supported by the New Century Excellent Talent Plan of the Ministry of Education of China

Received date: 2010-07-05; Accepted date: 2011-02-21

Corresponding author: PI Yang-jun, PhD; Tel: +86-571-87951271-6212; E-mail: zjuppbird@gmail.com