DOI: 10.11817/j.issn.1672-7207.2019.01.017
碾压混凝土的动态力学特性分析及损伤演化本构模型建立
张社荣1, 2,宋冉1, 2,王超1, 2,魏培勇1, 2
(1. 天津大学 水利工程仿真与安全国家重点实验室,天津,300350;
2. 天津大学 建筑工程学院,天津,300350)
摘要:为了深入认识碾压混凝土的动态力学特性,参考实际水工混凝土大坝工程制备试样,借助改进的分离式霍普金森压杆(SHPB)装置测定碾压混凝土的动态性能,得到不同级配碾压混凝土试样在动态冲击荷载下(应变率为25~80 s-1)的应力-应变曲线,分析其强度和变形特性、破坏形态和吸能特性,并建立基于Weibull分布的损伤演化本构模型。研究结果表明:碾压混凝土强度较低,加载过程中应力发展不充分,其应力-应变曲线呈现1个明显的平台阶段;碾压混凝土的峰值应力、峰值应变、单位体积吸能率均随加载应变率的提高而增大,并满足二次多项式关系;建立的统计损伤演化模型可以有效地描述碾压混凝土在动态冲击荷载下的力学行为,理论结果与实验结果吻合较好。
关键词:碾压混凝土;分离式霍普金森压杆实验;动态力学特性;统计损伤演化模型
中图分类号:TV41;TV431 文献标志码:A 文章编号:1672-7207(2019)01-0130-09
Dynamic mechanical property analysis of roller-compacted concrete and damage constitutive model establishment
ZHANG Sherong1, 2, SONG Ran1, 2, WANG Chao1, 2, WEI Peiyong1, 2
(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300350, China;
2. School of Civil Engineering, Tianjin University, Tianjin 300350, China)
Abstract: In order to explore the dynamic mechanical properties of roller-compacted concrete (RCC) comprehensively, actual hydraulic concrete dam project was referred to prepare specimen, and the dynamic mechanical properties of RCC were measured via improved split Hopkinson pressure bar (SHPB) technique. The stress-strain curves of two kinds of coarse grade specimens under dynamic loading (strain rate ranges from 20 s-1 to 80 s-1) were obtained. Then the strength and deformation characteristics, failure mode and energy absorption property were analyzed and a statistical damage constitutive model based on Weibull distribution was established. The results show that since RCC has low strength and the stress develops inadequately during experiment, the stress-strain curve shows an obvious plateau stage; the relationships between the peak stress, the peak strain, the energy absorption property and the loading strain rate are in accordance with two-polynomial relation, and all of them increase with the increment of the strain rate; the statistical damage constitutive model can well describe the mechanical behavior under dynamic impact loading. Theoretical results are in good agreement with experimental data.
Key words: roller-compacted concrete; split Hopkinson pressure bar experiment; dynamic mechanical properties; statistical damage evolution model
碾压混凝土在工程建设中的应用起源于美国,用于重负载路面,我国于20世纪80年代起开始研究该材料的性能并将其应用于水利工程建设中[1]。目前,一大批100~300 m级的高碾压混凝土坝正在建设或者将要兴建,大坝在服役期间可能遭受由地震、爆炸和恐怖袭击等灾害引起的高应变率荷载而失事,其后果将不堪设想,因此,碾压混凝土大坝抗爆安全问题亟需重视[2]。目前,对工程结构抗爆防爆的研究主要集中于工业和民用建筑[3-4],但大体积混凝土结构受爆炸冲击荷载作用的动态响应少有涉及。在常规的混凝土结构设计中,通常将材料在静力荷载下的力学参数(如强度和弹性模量)提高一定的比例作为其动态力学参数来计算结构在极限载荷下的响应[5-6],而混凝土大坝不同部位的应力状态在承受高应变率载荷时往往差异明显,上述确定动态力学参数的方法并不合理。随着碾压混凝土坝在水利工程建设中越来越多的采用,如我国的江垭水电站、龙滩水利枢纽工程、官地水电站和黄登水电站的拦河大坝均为碾压混凝土重力坝,其中官地和黄登水电站在设计过程中均进行了专门的防爆研究,为了更好地支撑大体积混凝土结构的抗爆设计,有必要进一步研究碾压混凝土材料的动态力学性能[7]。近几十年来已有很多学者对爆炸和冲击荷载作用下混凝土结构的力学行为进行了研究,尤其是大量的单轴实验被用于测定混凝土材料的动态力学特性[8-11]。混凝土材料的抗压强度和抗拉强度均表现出应变率增强效应,且骨料的含量、性质以及级配均对其有一定程度的影响[12-14]。由于混凝土类材料自身的复杂性及其在高应变率荷载下应力状态的不确定性,目前常见的动态力学本构模型如HJC模型、RHT模型、CSC模型和K&C模型等均涉及大量的参数,而其确定往往需要各种类型的力学实验数据[15-16],并难以直接用于工程结构的设计中。基于损伤理论的统计分布模型因参数较少、表达精简更有利于方便地描述材料的本构关系,目前对混凝土类材料损伤本构模型方面已有较多研究成果[17-18]。而对于高应变率加载的情况尤其涉及碾压混凝土这一具备特有的组分配比、成层特性和碾压振动施工工艺等特点的材料研究很少,为了探求能够合理描述碾压混凝土在高应变率下的损伤本构关系并用于实际工程设计中,需要开展动态力学实验并对其进行专门的研究。基于上述原因,本文作者依托实际碾压混凝土大坝工程的材料配比和施工方式制备碾压混凝土试样,采用改进的分离式霍普金森压杆装置对碾压混凝土试样的动态压缩特性进行测定,分析材料的动态力学参数,并基于连续介质的损伤理论建立碾压混凝土Weibull损伤本构模型[19]。
1 碾压混凝土SHPB实验
目前,分离式霍普金森压杆(SHPB)实验主要用于研究高应变率下混凝土材料的动态力学性能,并进一步确定各种动态本构模型的参数。
1.1 试样制备
实验用试样的制备参考黄登水电站碾压混凝土的配比和浇注方式。主供材料如下:水泥(祥云中热42.5号硅酸盐水泥)、粉煤灰(贵州火焰Ⅱ级)、河砂、人造粗骨料、减水剂(江苏博特JM-IIRCC)和引气剂(云南晨磊HLAE)。使用DC-25C手持式压路机对混凝土拌合料分层摊铺碾压,层厚为10 cm。共制备了2种级配的碾压混凝土试样,在温度为33 ℃和相对湿度为95%的条件下养护90 d,之后钻取、切割、打磨得到直径×长度为100 mm×200 mm和100 mm×50 mm的圆柱体试样,其中100 mm×200 mm的试样为测定碾压混凝土静态抗压强度的标准试件,100 mm×50 mm的试样用于测定碾压混凝土的动态压缩特性。表1所示为2种级配碾压混凝土试样的配合比。
表1 2种级配碾压混凝土试样的配合比
Table 1 Mix proportion of RCC with two kinds of gradation aggregates

1.2 SHPB实验原理及改进
此次实验使用的100mm直径SHPB装置能够满足如下假定:1) 压杆中应力波为一维状态;2) 试样中应力均匀;3) 波导杆中应力波为平面应力波;4) 波导杆在实验过程中为线弹性状态。碾压混凝土实验的应力、应变、应变速率和时间之间的关系可以由“三波法”[20]求得,如下式所示:
 (1)
(1)
式中: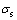 ,
, 和
和 分别为混凝土试样的应力、应变和应变率;
分别为混凝土试样的应力、应变和应变率; 为入射波应变;
为入射波应变; 为反射波应变;
为反射波应变; 为透射波应变;
为透射波应变; 为压杆横截面积;Ec为压杆弹性模量,试验中压杆为高强弹簧钢,弹性模量为200 GPa;c0为压杆中的弹性波速;As为试样横截面积;ls为试样高度。
为压杆横截面积;Ec为压杆弹性模量,试验中压杆为高强弹簧钢,弹性模量为200 GPa;c0为压杆中的弹性波速;As为试样横截面积;ls为试样高度。
实验测试前,在入射杆和透射杆上距离试件2.5 m和1.0 m位置黏贴应变片,通过惠更斯电桥接入超动态应变仪,得到加载过程中的应变信号。在SHPB实验中往往存在横向惯性效应引起的应力波形弥散,使用脉冲整形方法,即在入射杆受冲击端面安装一圆形的硬纸片使得入射波形由矩形波变为半正弦波,从而实现高频滤波。图1所示为是否使用脉冲整形器2种情况下的空打波形。由图1可见:整形后入射波上升沿减缓,波形弥散显著降低,目前对于脆性材料大直径SHPB实验加载技术的研究表明,波形整形技术已实现了近似恒应变率加载[21-22]。
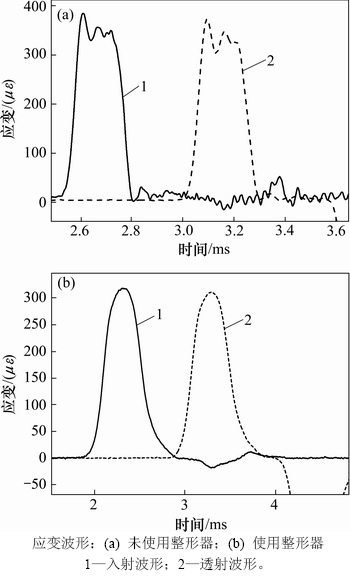
图1 入射杆和透射杆中的应变波形
Fig. 1 Strain waveform in incident and transmitted bars
1.3 实验过程
将碾压混凝土试样置于入射杆和透射杆间,在试样两端涂抹凡士林以保证其和压杆紧密接触,同时消除摩擦的影响。调整加载气压可以实现不同应变率的加载,打击杆以一定速度撞击入射杆,在入射杆中产生一个压缩波(入射波),入射波沿入射杆传播到试件与入射杆接触面,由于试件与压杆的波阻抗不同,会产生波的反射与透射,反射波沿入射杆往回传播;同时,透射波沿透射杆向前方传播。
考虑到碾压混凝土强度相对较低,为了保证实验的有效性,选取加载应变率30,50和70 s-1(相应的加载压力分别为0.15,0.22和0.30 MPa)分别对2种级配的试样进行冲击实验。选取3种应变率下二级配碾压混凝土试样分别为6,8和6个进行实验;三级配试样分别为6,5和7个,共计38个试样。
2 基本动态力学参数分析
2.1 SHPB实验结果
表2所示为2种级配碾压混凝土的准静态压缩实验和SHPB实验的结果。其中SEA(specific energy absorption)代表单位体积碾压混凝土在破坏过程中吸收的能量。由表2可以看出:对于大部分试样,峰值应力、峰值应变(峰值应力对应的应变)以及SEA随着平均加载应变率的增加而增加,但因碾压混凝土材料离散性较大,个别试样的结果存在例外。
2.2 试样破坏形态
图2和图3所示分别为2种级配碾压混凝土在不同应变率加载下试样的最终破坏形态。由图2和图3可见:在高速冲击荷载下,碾压混凝土试样因侧向约束作用由单轴应力状态转变为单轴应变状态,在加载过程中试样中应力来不及释放从而产生了拉伸破坏。在应变率为30 s-1和50 s-1左右时,试样的最终破坏形态表现出一定的成核现象,在加载过程中应变速率逐渐增加,破坏从试样表面发展到中心;当平均加载应变率达到70 s-1时,试样呈现出更加严重的破坏趋势,直至全部碎裂而丧失承载能力。2种级配的碾压混凝土试样在相近应变率下的破坏模式基本一致。
表2 2种级配碾压混凝土试样的SHPB实验结果
Table 2 SHPB experimental results of RCC specimens with two kinds of aggregate grading
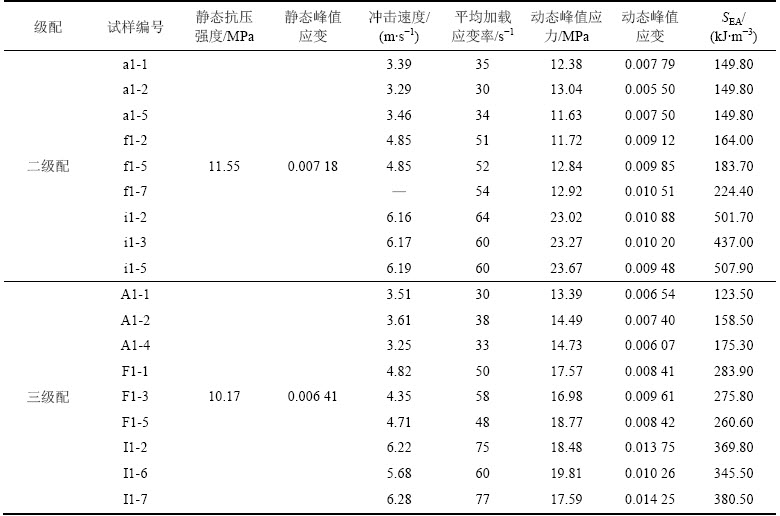

图2 二级配碾压混凝土试样破坏形态
Fig. 2 Failure patterns of RCC specimens of two grading

图3 三级配碾压混凝土试样破坏形态
Fig. 3 Failure patterns of RCC specimens of three grading
2.3 强度和变形特性
图4和图5所示分别为2种级配碾压混凝土试样在不同加载应变率下的应力-应变关系曲线。从图4和图5可见:应力-应变关系在初始阶段接近线性,应力缓慢增加直至峰值, 随后应力随着应变的继续增加而缓慢下降,下降过程近似与上升过程对称;当入射波到达试样时,其应力瞬间上升而应变几乎不受影响;碾压混凝土的应力-应变曲线存在一应力几乎恒定的平台阶段,这主要是碾压混凝土材料中的水泥砂浆与粗骨料凝聚性较弱,裂缝的形成和发展并非由应力的增长造成,而主要是由随应变逐渐累积的损伤引起;当应力达到峰值时,应变急剧增大且试样中的裂纹急速发展,并伴随着大量能量的消散直到试样完全失效。
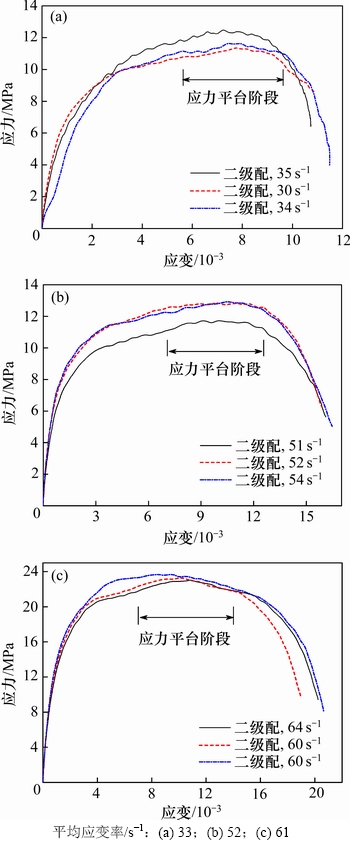
图4 二级配碾压混凝土试样的应力-应变曲线
Fig. 4 Stress-strain curves of RCC specimens of two grading

图5 三级配碾压混凝土试样的应力-应变曲线
Fig. 5 Stress-strain curves of RCC specimens of three grading
混凝土类材料在高应变率荷载作用下的抗压强度会表现出不同程度的增强现象,图6所示为2种级配碾压混凝土试样的峰值应力和应变率的关系,由于材料离散性较大,拟合曲线时剔除了个别数据点。在加载应变率为20~80 s-1范围内,峰值应力在7.30~28.83 MPa之间变化。拟合得到的峰值应力与应变率的关系为
 (2)
(2)
碾压混凝土是一种分布有初始裂纹和孔洞的不连续性异质材料,随着加载过程中应力波的传播,这些缺陷会逐渐发展并最终导致试样断裂。由于高应变率加载过程迅速,微裂纹来不及发展,且在快速压缩下因压杆/试样接触作用及惯性效应产生横向约束,材料的应力会急剧增加,这也反映了试样由单轴应力状态转变为单轴应变状态。三级配的试样粗骨料级配连续,砂浆和粗骨料更加密实,因此,整体强度较二级配的高。

图6 碾压混凝土峰值应力与应变率关系
Fig. 6 Dynamic compressive strength of RCC at different strain rates
碾压混凝土试样的变形特性主要考虑其峰值应变,图7所示为应变率在20~80 s-1范围内2种级配碾压混凝土的峰值应变。峰值应变具有明显的应变率依赖性,其变化范围在4.0×10-3~16.0×10-3之间。峰值应变与加载应变率的关系如下:
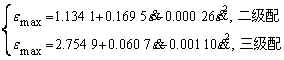 (3)
(3)
2种级配的碾压混凝土峰值应力与应变率关系大致相同。在较大的加载应变率下试样的抗压强度增加,试样内部更加密实,需要更大的变形以吸收足够的能量。图7所示碾压混凝土试样的峰值应变均大于5×10-3,超过了其在静态压缩实验下的值(3×10-3),表明了高应变率加载下峰值应变增加。
2.4 吸能特性
采用单位体积试样吸收的能量(SEA,单位为J/m3)来描述碾压混凝土在破坏过程中的能量吸收特性,根据下式对应变波形进行积分计算可求得SEA:
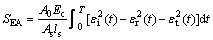 (4)
(4)
式中:T为入射应变波形、反射应变波形和透射应变波形经对齐后,波头至波尾的长度,SEA可由入射波形、透射波形和反射波形积分求得。
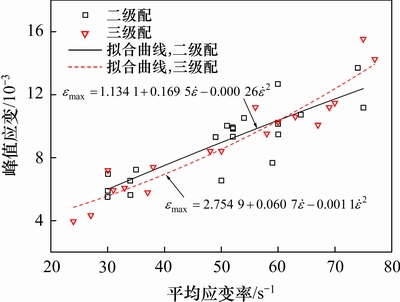
图7 碾压混凝土峰值应变与应变率关系
Fig. 7 Critical strain of RCC at different strain rates
图8所示为碾压混凝土试样的单位体积吸能率。从图8可知:当应变速率从20 s-1变化到110 s-1时,碾压混凝土试样的SEA为123.5 ~507.9 kJ/m3。SEA与平均加载应变率之间的拟合关系如下:
 (5)
(5)
图8中的SEA表示单位体积试样在相应应变率下能够吸收的最大能量,综合反映了碾压混凝土试样的强度和变形特性,超过该值则发生破坏;当平均加载应变率较大时,试样在破坏过程中吸收的能量也随之增多,说明产生了更多的微裂纹和孔洞,试样表现出更大的强度和变形。
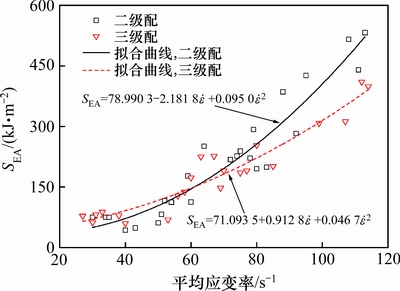
图8 碾压混凝土试样的单位体积吸能率
Fig. 8 SEA of RCC at different strain rates
3 基于统计理论的损伤演化本构模型
3.1 连续介质的损伤理论
碾压混凝土是一种各向异性的脆性材料,初始缺陷的存在及其在荷载作用下的发展导致了裂纹的产生直至破坏。损伤力学理论可以有效地描述材料的非线性渐进破坏过程[23],因此,采用各向同性损伤表达式来评估碾压混凝土在冲击荷载下的力学行为:
 (6)
(6)
式中:D为累积损伤率,可与应变张量共同反映材料的受力状态;Vc为破坏区域所占的体积;V0为总体积。当试样中某处的应变达到临界应变时认为发生破坏,剩余未破坏的区域( )将承受全部冲击荷载,此时,应力-应变关系可表述如下:
)将承受全部冲击荷载,此时,应力-应变关系可表述如下:
 (7)
(7)
式中: 和
和 分别为未破坏区域的应力和应变;E为弹性模量,取SHPB实验得到的应力-应变曲线对应20%峰值应变和40%峰值应变处2点的斜率。
分别为未破坏区域的应力和应变;E为弹性模量,取SHPB实验得到的应力-应变曲线对应20%峰值应变和40%峰值应变处2点的斜率。
3.2 Weibull统计分布
碾压混凝土材料的强度分布可由Weibull分布方程表述如下:
 (8)
(8)
式中:F0和m分别为双参数Weibull分布中的尺度参数和形状参数。将式(8)代入式(7)可得
 (9)
(9)
对式(9)两边取两次对数得到
 (10)
(10)
式(10)可以看作是关于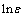 和
和 的线性函数,由SHPB实验所得的应力和应变采用最小二乘法对式(10)进行拟合,参数F0和m可根据截距和斜率求得[24]。
的线性函数,由SHPB实验所得的应力和应变采用最小二乘法对式(10)进行拟合,参数F0和m可根据截距和斜率求得[24]。
3.3 碾压混凝土损伤本构模型
由于组成成分的复杂性和初始孔洞等缺陷的存在,碾压混凝土材料的力学行为分布表现出较大的随机性,可以认为碾压混凝土的强度是1个多因素联合导致的随机变量并符合统计规律。WANG等[25]对钢纤维混凝土的Weibull参数研究结果表明其与加载应变率的对数呈线性关系,根据2.1中2种级配碾压混凝土在不同应变率下的应力-应变曲线,将已知的实验应力 和应变
和应变 代入式(10),得到1条斜率为m、截距为
代入式(10),得到1条斜率为m、截距为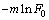 的曲线,采用线性回归分析法进行拟合求得m和
的曲线,采用线性回归分析法进行拟合求得m和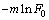 ,即可求得相应的F0和m,二者和应变率的关系如下。
,即可求得相应的F0和m,二者和应变率的关系如下。
 (11)
(11)
根据式(11)计算2种级配碾压混凝土在不同加载应变率下的Weibull参数,代入式(10)后可得到理论计算的应力-应变曲线,如图9所示。基于上述损伤模型得到的关系曲线与实验值(相近应变率下3组实验数据的平均结果)吻合较好,说明Weibull统计分布可以有效地描述碾压混凝土的强度分布。图9中应力-应变曲线末端已处于结构破坏阶段,由于并非是材料自身性质的反映,因此,理论计算值与实验值存在差异。

图9 理论曲线与实验曲线的对比
Fig. 9 Comparison between experimental and theoretical curves
4 结论
1) 建立了适用于测定碾压混凝土动态压缩特性的改进SHPB实验技术,水工上使用的碾压混凝土强度较一般的常态混凝土低(2种级配碾压混凝土的静态压缩强度分别为11.55 MPa和10.17 MPa),且在加载过程中应力发展不充分,因此,碾压混凝土的动态应力-应变曲线呈现1个明显的平台阶段。
2) 碾压混凝土试样在冲击荷载下的破坏从边缘向中心发展,并呈现出留核现象,峰值应力、峰值应变、单位体积吸能率均表现出明显的率相关性,其与加载应变率均为近似的二次多项式关系。
3) 依据统计损伤理论建立的理论模型可以较好地描述碾压混凝土的基本动态压缩特性,理论应力-应变关系与实验结果吻合较好,说明Weibull统计分布可以有效地描述碾压混凝土的强度分布,由于模型涉及的参数较少,可以方便地利用该模型评估碾压混凝土的动态压缩特性。模型中的参数F0和m是对特定级配碾压混凝土和应变率条件下回归所得,未考虑试样初始缺陷和骨料分布的影响,要全面地描述碾压混凝土本构关系还需进一步从细观角度进行研究。
参考文献:
[1] 席浩. 碾压混凝土研究与工程实践[M]. 北京: 中国水利水电出版社, 2015: 8-15.
XI Hao. Research and engineering practice of roller-compacted concrete[M]. Beijing: China Water & Power Press, 2015: 8-15.
[2] 陆遐龄. 三峡工程防护问题研究的回顾[J]. 中国三峡建设, 1995(2): 23-24.
LU Xialing. Review on the protection of Three Gorges Project[J]. China Three Gorges Construction, 1995(2): 23-24.
[3] GEORGIN J F, REYNOUARD J M. Modeling of structures subjected to impact: concrete behavior under high strain rate[J]. Cement and Concrete Composites, 2003, 25(1): 131-143.
[4] NGO T, MENDIS P, GUPTA A, et al. Blast loading and blast effects on structures–an overview[J]. Electronic Journal of Structural Engineering, 2007, 7(S1): 76-91.
[5] United States Army Corps of Engineers. Structures to resist the effects of accidental explosions[M]. Washington DC: US Government Printing Office, 1969: 45-47.
[6] 中国电力出版社. 水工建筑物抗震设计规范[M]. 北京: 中国电力出版社, 2001: 16-17.
China Electric Power Press. Code for seismic design of hydraulic structures[M]. Beijing: China Electric Power Press, 2001: 16-17.
[7] BISCHOFF P H, PERRY S H. Compressive behavior of concrete at high strain rates[J]. Materials and structures, 1991, 24(6): 425-450.
[8] PETERS J, ANDERSON W F, WASTON A J. Use of large diameter Hopkinson bar to investigate the stress pulse generated during high velocity projectile penetration into construction materials[C]// Proceedings of the 6th International Symposium on Interaction of Nonnuclear Munitions with Structures. Florida, USA, 1993: 188-193.
[9] 王怀亮, 闻伟. 碾压混凝土单轴动态力学性能研究[J]. 水力发电学报, 2011, 30(4): 155-167.
WANG Huailiang, WEN Wei. Dynamic mechanical properties of RCC under uniaxial stress[J]. Journal of Hydroelectric Engineering, 2011, 30(4): 155-167.
[10] 张志刚, 孔大庆, 宫光明, 等. 高应变率下混凝土动态力学性能SHPB实验[J]. 解放军理工大学学报(自然科学版), 2007, 8(6): 611-618.
ZHANG Zhigang, KONG Daqing, GONG Guangming, et al. Dynamic mechanical behavior of concrete under high strain rate using SHPB[J]. Journal o f PLA University of Science and Technology, 2007, 8(6): 611-618.
[11] 王政, 倪玉山, 曹菊珍, 等. 冲击载荷下混凝土动态力学性能研究进展[J]. 爆炸与冲击, 2005, 25(6): 519-527.
WANG Zheng, NI Yushan, CAO Juzhen, et al. Recent advances of dynamic mechanical behavior of concrete under impact loading[J]. Explosion and Shock Waves, 2005, 25(6): 519-527.
[12] MALVAR L J, ROSS C A. Review of strain rate effects for concrete in tension[J]. Materials Journal, 1998, 95(6): 735-739.
[13] GROTE D L, PARK S W, ZHOU M. Dynamic behavior of concrete at high strain rates and pressures: I. experimental characterization[J]. International Journal of Impact Engineering, 2001, 25(9): 869-886.
[14] HAO H, ZHOU X Q. Concrete material model for high rate dynamic analysis[C]// Proceedings of the 7th International Conference on Shock and Impact Loads on Structures. Perth, Australia, 2007: 753-768.
[15] 余志武, 吴玲玉, 单智. 混凝土确定性及随机性损伤本构模型研究进展[J]. 工程力学, 2017, 34(9): 1-12.
YU Zhiwu, WU Lingyu, SHAN Zhi. Models for deterministic and stochastic damage constitutions of concrete: a short review[J]. Engineering Mechanics, 2017, 34(9): 1-12.
[16] CUI Jian, HAO Hong, SHI Yanchao. Discussion on the suitability of concrete constitutive models for high-rate response predictions of RC structures[J]. International Journal of Impact Engineering, 2017, 106: 202-216.
[17] 彭向和, 杨春和. 复杂加载史下混凝土的损伤及其描述[J]. 岩石力学与工程学报, 2000, 19(2): 157-164.
PENG Xianghe, YANG Chunhe. The damage and its description of concrete under complex loading history[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(2): 157-164.
[18] 邹笃建, 刘铁军, 滕军, 等. 混凝土柱单轴动态抗压特性的应变率效应研究[J]. 振动与冲击, 2012, 31(2): 145-150.
ZOU Dujian, LIU Tiejun, TENG Jun, et la. Strain rate effect on uniaxial compressive behavior of concrete columns[J]. Journal of Vibration and Shock, 2012, 31(2): 145-150.
[19] TSU T C, MUGELE R A, MCCLINTOCK F A. A statistical distribution function of wide applicability[J]. Journal of Applied Mechanics-Transactions of the Asme, 1952, 19(2): 233-234.
[20] 宋力, 胡时胜. SHPB数据处理中的二波法与三波法[J]. 爆炸与冲击, 2005, 25(4): 368-373.
SONG Li, HU Shisheng. Two-wave and three-wave method in SHPB data processing[J]. Explosion and Shock Waves, 2005, 25(4): 368-373.
[21] 卢玉斌, 武海军, 李庆明, 等. 脆性材料SHPB实验中脉冲整形技术实现近似恒应变率加载功能的进一步研究[J]. 爆炸与冲击, 2013(s1): 47-53.
LU Yu-bin, WU Hai-jun, Li Qing-ming, et al. Further investigation on nearly constant strain-rate loading in SHPB tests for brittle materials using a pulse-shaping technique[J]. Explosion and Shock Waves, 2013(s1): 47-53.
[22] 李为民, 许金余, 沈刘军, 等. Φ100 mm SHPB应力均匀及恒应变率加载试验技术研究[J]. 振动与冲击, 2008, 27(2): 129-132.
LI Weimin, XU Jinyu, SHEN Liujun, et al. Study on 100-mm-diameter SHPB techniques of dynamic stress equilibrium and nearly constant strain rate loading[J]. Journal of Vibration and Shock, 2008, 27(2): 129-132.
[23] MAZARS J, PIJAUDIER-CABOT G. Continuum damage theory-application to concrete[J]. Journal of Engineering Mechanics, 1989, 115(2): 345-365.
[24] 李晓雨. 三参数Weibull分布参数估计方法研究[D]. 北京: 北京交通大学理学院, 2012: 3-12.
LI Xiaoyu. Research on estimation for the three-parameter Weibull distribution[D]. Beijing: Beijing Jiaotong University. School of Science, 2012: 3-12.
[25] WANG Z L, LIU Y S, SHEN R F. Stress–strain relationship of steel fiber-reinforced concrete under dynamic compression[J]. Construction and Building Materials, 2008, 22(5): 811-819.
(编辑 杨幼平)
收稿日期:2018-01-23;修回日期:2018-03-29
基金项目(Foundation item):国家自然科学基金资助项目(51779168,51509182) (Projects(51779168, 51509182) supported by the National Natural Science Foundation of China)
通信作者:宋冉,博士研究生,从事水工结构静动力分析计算、混凝土材料动态力学特性研究;E-mail: songraneterno@tju.edu.cn