J. Cent. South Univ. (2021) 28: 1402-1411

DOI: https://doi.org/10.1007/s11771-021-4701-2

Tooth surface error correction of hypoid gears machined by duplex helical method

WU Shun-xing(吴顺兴)^{1, 2}, YAN Hong-zhi(严宏志)¹, WANG Zhi-yong(王志永)³,BI Ren-gui(毕仁贵)², CHEN Zhi(陈志)¹, ZHU Peng-fei(朱鹏飞)¹

1. State Key Laboratory for High Performance Complex Manufacturing, Central South University,Changsha 410083, China;

2. College of Physics and Electromechanical Engineering, Jishou University, Jishou 416000, China;

3. College of Mechanical and Electrical Engineering, Central South University of Forestry and Technology, Changsha 410004, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021

Abstract: In this work, synchronous cutting of concave and convex surfaces was achieved using the duplex helical method for the hypoid gear, and the problem of tooth surface error correction was studied. First, the mathematical model of the hypoid gears machined by the duplex helical method was established. Second, the coordinates of discrete points on the tooth surface were obtained by measurement center, and the normal errors of the discrete points were calculated. Third, a tooth surface error correction model is established, and the tooth surface error was corrected using the Levenberg–Marquard algorithm with trust region strategy and least square method. Finally, grinding experiments were carried out on the machining parameters obtained by Levenberg–Marquard algorithm with trust region strategy, which had a better effect on tooth surface error correction than the least square method. After the tooth surface error is corrected, the maximum absolute error is reduced from 30.9 μm before correction to 6.8 μm, the root mean square of the concave error is reduced from 15.1 to 2.1 μm, the root mean square of the convex error is reduced from 10.8 to 1.8 μm, and the sum of squared errors of the concave and convex surfaces was reduced from 15471 to 358 μm². It is verified that the Levenberg–Marquard algorithm with trust region strategy has a good accuracy for the tooth surface error correction of hypoid gear machined by duplex helical method.

Key words: duplex helical method; hypoid gear; error measurement; Levenberg–Marquard algorithm with trust region strategy; correction of tooth surface error

Cite this article as: WU Shun-xing, YAN Hong-zhi, WANG Zhi-yong, BI Ren-gui, CHEN Zhi, ZHU Peng-fei. Tooth surface error correction of hypoid gears machined by duplex helical method [J]. Journal of Central South University, 2021, 28(5): 1402-1411. DOI: https://doi.org/10.1007/s11771-021-4701-2.

1 Introduction

Owing to the influence of factors such as machining error, deformation caused by force and heat, the tooth surface of hypoid gear deviates from the designed tooth surface, which affects the transmission quality of the gear pair, and ultimately reduces the stability and durability of the car. In order to obtain a high precision tooth surface, the coordinate of discrete points on the tooth surface is obtained using three-coordinate measurement, and an error correction model is established to correct the machining parameters, which is an effective method to achieve compensation of tooth surface error [1-5]. At present, some scholars have done some research on tooth surface error correction. LITVIN et al [6] established an error sensitive matrix of machining parameters increments, and minimized tooth surface errors by modifying the machining parameters. WANG et al [7] established a tooth shape error correction method based on proportional correction parameters to correct the tooth surface error, avoiding the solution of complex equations. TIAN et al [8] selected correction variables by analyzing the linear correlation between each machining parameter and the measured error, so that fewer machining parameters were selected to correct the tooth surface error. SU et al [9] established a tooth surface error correction model based on numerical control, machining tool. Through multiple optimizations and changing the weighting coefficients, it is possible to obtain higher precision correction requirements for tooth surfaces. LI et al [10] established a mapping relationship between machine tool motion parameters and tooth surface errors, and minimized tooth surface errors through automatic correction of machine tool motion parameters. SHIH et al [11, 12] and JIANG et al [13] used numerical control machine tools to make high-order corrections to the tooth surface error. In terms of the algorithm used to correct the tooth surface error, the least square method was first used [6]. Subsequently, in order to improve the stability and accuracy of the solution, singular value decomposition singular value decomposition [14, 15] and sequential quadratic program [16] methods were proposed. But for excessive morbidity problems, Levenberg–Marquard [17-19] has a better effect.

The above literatures on the tooth surface error correction of spiral bevel gears are mainly aimed at the spiral bevel gears cut by the five-cut method, and limited research has been conducted on the duplex helical method. When using the five-cut method, the concave and convex surfaces are cut separately, so the error correction of the tooth surface is easy relatively. However, the duplex helical method has the characteristics of concave and convex surfaces simultaneous cutting, it is more difficult to obtain accurate tooth surfaces compared with the five-cut method. Moreover, due to the characteristics of high processing efficiency and good quality consistency, the duplex helical method is replacing the five-cut method as the mainstream machining method of hypoid gears [20]. Therefore, it is the main purpose of this paper to study the tooth surface error correction method of hypoid gears machining by duplex helical method.

2 Mathematical model of hypoid gear machining by duplex helical method

The concave and convex cutting cones of pinion are shown in Figure 1. The coordinate systems applied for the pinion generation are shown in Figure 2, where S_p is a coordinate system rigidly fixed to the head cutter; S_a is the auxiliary coordinate system; S_m1, S_c and S_d are fixed coordinate systems rigidly fixed to the cutting machine; S_b and S₁ are the movable coordinate systems rigidly fixed to the cradle and pinion, respectively; q₁, s_r1, i, and j represent the center roll position, radial distance, tilt angle, and swivel angle, respectively; e₁, x_b1, m₁, x_g1, m_b1 and hl represent the work offset, sliding base, machine root angle, the machine center to the cross point, ratio of roll and the velocity coefficient of helical motion, respectively; φ is the rotation angle of the pinion. When the pinion is cut by the duplex helical method, the cradle rotates around the axis z_m1 while moving as a helix along the axis z_m1.

Figure 1 Concave and convex cutting cone of pinion:

Figure 2 Coordinate systems applied for pinion generation

Simultaneously, the pinion makes a rotary motion around the axis x_d. The mathematical model of the tooth surface of pinion machined by the duplex helical method is derived as follows:

First, the vector function r_p and its unit normal n_p of the cutting point on the cutting cone for the pinion cutter are established. As shown in Figure 1, in the s_p coordinate system, r_p and n_p can be expressed as [21-23]:

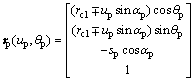             (1)

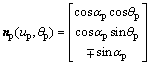                   (2)

where s_p and θ_p are the Gaussian coordinates of the pinion tooth surface, α_p and r_c1 are the blade angle and cutter point radius, respectively. The upper and lower signs in Eqs. (1) and (2) correspond to the convex and tooth surface error correction concave surfaces of the pinion.

Then, the r_p and n_p are converted into the coordinate system S₁ according to the coordinate systems applied for the pinion generation shown in Figure 2. As a result, the tooth surface equation r and its unit normal vector n of the pinion in the coordinate system S₁ can be obtained by the following equation:

                  (3)

where matrix M_1p represents the transformation matrix from the coordinate system S_p to S₁, and matrix L_1p is the third-order submatrix of matrix M_1p. M_1p and L_1p can be expressed as:

                    (4)

                        (5)

where q=q₁+φ·m_b1, x_b=x_b0-hl·φ·m_b1.

In addition, the meshing equation should be satisfied when forming a pinion [24, 25]:

         (6)

Combine Eqs. (2) and (6) to eliminate the variable up, and the tooth surface equation of pinion can be expressed as [26]:

                          (7)

where ξ_l (l=1, 2, …, 10) represents the machining parameters of the machine tool q₁, s_r1, m_b1, γ_m1, x_b1, x_g1, e₁, hl, m_b1 and i.

3 Tooth surface dispersion and tooth surface error calculation

The tooth surface error is defined as the deviation of the actual tooth surface and the theoretical tooth surface in the normal vector direction of the theoretical tooth surface. And the tooth surface error needs to be compared at the same position of the actual tooth surface and the theoretical tooth surface. Therefore, the tooth surface needs to be discretized, that is, the tooth surface is divided into uniform grid points. Figure 3 shows the schematic diagram of tooth surface dispersion.

Figure 3 Schematic diagram of tooth surface dispersion

According to the Gleason technical standard, after shrinking the tooth surface, a total of 45 points in 5 rows and 9 columns are taken in the direction of tooth length and tooth height. The relationship between the coordinate (L, R) of the discrete point on the rotating projection surface and the tooth surface equation can be expressed as:

                              (8)

where p is the unit vector of the axis direction of the pinion. According to the geometric parameters of the pinion blank, the discrete point coordinates (L, R) on the rotation projection surface can be obtained, and then the simultaneous Eqs. (7) and (8) can obtain the radial vector r_t (x, y, z) and normal vector n_t (x,y,z) of the spatial coordinates for the discrete points. The coordinate r_t^* (x, y, z) of the discrete points can be obtained using the coordinate measuring system. Therefore, the calculation formula of the normal error for the tooth surface can be expressed as:

  (9)

where t=1, 2, …, 90.

It is worth noting that the normal error of the tooth surface is calculated in the measurement coordinate system. Therefore, it is necessary to convert the discrete point coordinates of the theoretical tooth surface into the coordinate system of the three-coordinate measuring system. When the pinion is machined by the duplex helical method, the concave and convex surfaces are cut simultaneously. Therefore, t in Eq. (9) is 90 discrete points, and ε_t is expressed as the normal error of the 90 discrete points on the tooth surface.

4 Influence of machining parameters on tooth surface error

In order to analyze the influence of machining parameters on the tooth surface error. Let the angle change to 0.05°, the linear parameter change to 0.05 mm, and the roll ratio parameter to 0.005. Figures 4-13 show the corresponding tooth surface error ease-off diagrams when 10 machining parameters change.

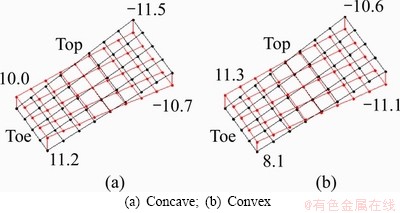
Figure 4 Radial distance s_r1:(Unit: μm)

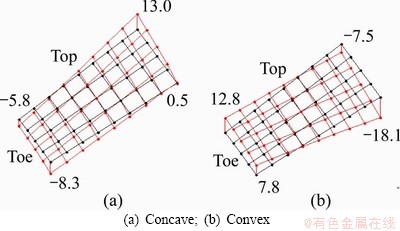
Figure 5 Tilt angle i:(Unit: μm)

Figure 6 Swivel angle j:(Unit: μm)

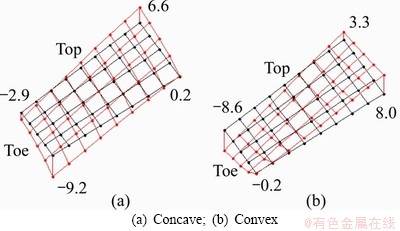
Figure 7 Work offset e₁:(Unit: μm)

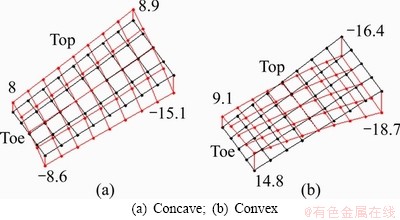
Figure 8 Machine root angle γ_m1:(Unit: μm)

Figure 9 Machine center to back x_g1:(Unit: μm)

Figure 10 Sliding base x_b1:(Unit: μm)

It can be seen from Figures 4-13 that the machining parameters that have an influence on the helix angle error include radial distance, sliding base and center roll position, of which the radial distance has the greatest influence on the helix angle error. The machining parameters that have influence on the diagonal error are tilt angle, swivel angle, work offset, ratio of roll and velocity coefficient of helical motion, of which the ratio of roll has the greatest influence on the diagonal error. The machine root angle and the machine center to back have different effects on the error shape of the concave and convex surfaces. And the concave and convex surfaces of the machine center to back have an effect on the pressure angle error and the diagonal error, respectively. In the subsequent tooth surface error correction process, the influence of machining parameters on the tooth surface error can provide a theoretical reference for parameter selection and initial value selection.

Figure 11 Ratio of roll m_b1:(Unit: μm)

Figure 12 Center roll position q₁:(Unit: μm)

Figure 13 Velocity coefficient of helical motion hl:(Unit: μm)

5 Tooth surface error correction model

When machining parameters have errors, the tooth surface will also produce errors. Therefore, the tooth surface error can be minimized by modifying the machining parameters of theoretical tooth surface. The tooth surface error of each discrete point of the theoretical tooth surface is the superposition of the tooth surface error caused by small changes in various machining parameters, that is, the total differentiation of Eq. (7):

   (10)

Multiply both sides of Eq. (10) by unit normal vector n, and the coordinate parameters θ and φ are located in the tangent plane of the tooth surface, so the normal error of the tooth surface can be obtained as:

                    (11)

Simultaneous Eqs. (9) and (11) establish the minimum optimization model of tooth surface error:

                   (12)

where Δξ_l is the correction amount of the machining parameters after the tooth surface error correction. The implementation of the Levenberg–Marquard algorithm with trust region strategy is to introduce the damping coefficient to control the size and direction of the iteration step within the radius of the trust region, thereby ensuring that each iteration step is accurate and efficient. Therefore, in this paper, the Levenberg–Marquard algorithm with trust region strategy [27] is used to solve Eq. (12), among them, when updating the radius of the trust region, tangent single dogleg method is selected [28].

6 Numerical examples and verification

Take the hypoid gear pair as an example, in which the gear is machined by the forming method, and the pinion is machined by the duplex helical method, and the tooth surface error of the pinion is corrected. It is worth noting that in order to ensure that the cutter head and the set of machine parameters can synchronously control the meshing characteristics of concave and convex when the duplex helical method is used to machine the pinion, the design and cutting of the pinion need to meet the following two conditions. First, the tooth blank of the pinion should be designed for duplex tapered tooth depth. Second, the machine tool for machining pinion must have the functions of tilt and spiral motion, and the tilt and spiral motion can be obtained by using the five-axis linkage CNC spiral bevel gear machine tool. The main geometric parameters of the pinion are listed in Table 1. The initial values of machining parameters for the pinion are shown in Table 2. The discrete point measurement of tooth surface is shown in Figure 14. The initial tooth surface error diagram measured and calculated by the three-coordinate measuring system is shown in Figure 15. The Levenberg–Marquard algorithm with trust region strategy is used to correct the tooth surface error shown in Figure 15 and compared with the least square method used in Ref. [29]. When selecting the machining parameters that need to be corrected, it is better to select 10 machining parameters to correct the tooth surface error compared to selecting fewer machining parameters. The corrected values of the machining parameters after tooth surface error correction are listed in Table 3.

Table 1 Main geometric parameters of pinion

Table 2 Initial value of machining parameters for pinion

Figure 14 Discrete point measurement of tooth surface

Based on the corrected values of the machining parameters shown in Table 3, the theoretical tooth surface errors corrected by Levenberg–Marquard algorithm with trust region strategy and least square method are calculated respectively. After the tooth surface error is corrected, the maximum absolute value of normal errors corresponding to the Levenberg–Marquard algorithm with trust region strategy and the least square method are 5.0 and 6.7 μm, respectively. The sums of squared errors of the concave and convex surfaces corresponding to the Levenberg–Marquard algorithm with trust region strategy and the least square method are 251 and 626 μm², respectively. Therefore, the Levenberg–Marquard algorithm with trust region strategy has a better correction effect on the tooth surface error. In order to further check the actual effect of the Levenberg–Marquard algorithm with trust region strategy on the tooth surface error correction, the corrected machining parameters are used to grind the tooth surface on the eight-axis five-link CNC spiral bevel gear grinding machine H650GA. Figure 16 shows the actual tooth surface error diagram after grinding. Table 4 lists the initial and corrected tooth surface error data.

It can be seen from Table 4 that the corrected tooth surface error is greatly reduced, the maximum absolute error is reduced from 30.9 μm before correction to 6.8 μm, the root mean square of the concave error is reduced from 15.1 to 2.1 μm, the root mean square of the convex error is reduced from 10.8 to 1.8 μm, and the sum of squared errors of the concave and convex surfaces is reduced from 15471 to 358 μm². Correction effect fully meets engineering application requirements.

Figure 15 Initial tooth surface error diagram (Unit: μm)

Table 3 Correction value of machining parameters for pinion

Figure 16 Actual tooth surface error after grinding (Unit: μm)

Table 4 Initial and corrected tooth surface error data

7 Conclusions

In this work, the tooth surface error of hypoid gears cutting machined by the duplex helical method is corrected, and the tooth surface grinding experiment is carried out using the modified machining parameters. The conclusions are summarized as follows:

1) The mathematical model of the hypoid gears machined by the duplex helical method is established;

2) A tooth surface error correction model is established. The Levenberg–Marquard algorithm with trust region strategy and the least square method are used to correct the error tooth surface. Comparison shows that the Levenberg–Marquard algorithm with trust region strategy has a better effect on the tooth surface error correction.

3) The machining parameters obtained by the Levenberg–Marquard algorithm with trust region strategy are used to grind the tooth surface, and the following results are obtained. The corrected tooth surface error is greatly reduced. The maximum absolute error is reduced from 30.9 μm before correction to 6.8 μm, the root mean square of the concave error is reduced from 15.1 to 2.1 μm, the root mean square of the convex error is reduced from 10.8 to 1.8 μm, and the sum of squared errors of the concave and convex surfaces is reduced from 15471 to 358 μm². It is verified that the Levenberg–Marquard algorithm with trust region strategy has a good accuracy for the tooth surface error correction of hypoid gear processed by double helix method.

Contributors

The overarching research goals were developed by WU Shun-xing and YAN Hong-zhi. WU Shun-xing, WANG Zhi-yong and BI Ren-gui established the mathematical model of hypoid gear machining by duplex helical method and corrected the error of the tooth surface. CHEN Zhi and ZHU Peng-fei analyzed the calculated results. All the authors replied to reviewers’ comments and revised the final version.

Conflict of interest

WU Shun-xing, YAN Hong-zhi, WANG Zhi-yong, BI Ren-gui, CHEN Zhi and ZHU Peng-fei declare that they have no conflict of interest.

References

[1] DENG Xiao-zhong, LI Geng-geng, WEI Bing-yang. Face-milling spiral bevel gear tooth surfaces by application of 5-axis CNC machine tool [J]. International Journal of Advanced Manufacturing Technology, 2014, 71(8): 1049-1057. DOI: 10.1007/s00170-013-5499-3.

[2] LI Ju-bo, XU Ai-jun, XU Kai, ZHANG Hua, LI Tian-xing, YANG Jian-jun. Digital closed-loop manufacturing technology of spiral bevel gear based on networked integration [J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(16): 94-103. DOI: 10.11975/ j.issn.1002-6819.2015.16.013. (in Chinese)

[3] WANG Hui-liang, LI Ju-bo, YANG Gao, YANG Jian-jun. Closed-loop feedback flank errors correction of topographic modification of helical gears based on form grinding [J]. Mathematical Problems in Engineering, 2015: 635156. DOI: 10.1155/2015/635156.

[4] LI Tian-xing, LI Ju-bo, DENG Xiao-zhong, YANG Jian-jun, LI Geng-geng, MA Wen-suo. A new digitized reverse correction method for hypoid gears based on a one-dimensional probe [J]. Measurement Science and Technology, 2017, 28(7): 125004. DOI: 10.1088/1361-6501/aa8dd7.

[5] LI Ju-bo, MA Hui-jie, DENG Xiao-zhong, ZHANG Hua, YANG Jiang-Jun. An approach to realize the networked closed-loop manufacturing of spiral bevel gears [J]. International Journal of Advanced Manufacturing Technology, 2017, 89(8): 1469-1483. DOI: 10.1007/s00170-016-9200-5.

[6] LITVIN F L, KUAN C, WANG J C, HANDSCHUH R F. Minimization of deviation of gear real tooth surface determined by coordinate measurements [J]. Journal of Mechanical Design, 1993, 155(4): 955-1001. DOI: 10.1115/ 1.2919298.

[7] WANG Zhi-yong, ZENG Tao. Correction of tooth flank errors of spiral bevel gear based on proportional change parameters [J]. Journal of Mechanical Engineering, 2010, 46(1): 43-47. DOI: 10.3901/JME.2010.01.043.

[8] TIAN Cheng, DING Wei-qi, GUI Liang-jing, FAN Zhi-jie. Flank error correction of hypoid gears based on regression analyses [J]. Journal of Tsinghua University(Science and Technology), 2017, 57(2): 32-37. DOI: 10.16511/ j.cnki.qhdxxb.2017.22.005. (in Chinese)

[9] SU Jin-zhan, FANG Zong-de, GU Jian-gong. Tooth surface correction for spiral bevel gears [J]. Transactions of the Chinese Society of Agricultural Engineering, 2010, 41(3): 200-204. DOI: 10.3969/j.issn.1000-1298.2010.03.041.

[10] LI Tian-xing, DENG Xiao-zhong, LI Ju-bo, YANG Jian-jun. Automatic feedback correction and deviation analysis for tooth surface of spiral bevel and hypoid gear [J]. Journal of Aerospace Power, 2011, 26(5): 1194-1200. DOI: 10.13224/ j.cnki .jasp.2011.05.011. (in Chinese)

[11] SHIH Y P, SUN Z H, LAI K L. A flank correction face-milling method for bevel gears using a five-axis CNC machine [J]. The International Journal of Advanced Manufacturing Technology, 2017, 91(9): 3635-3652. DOI: 10.1007/ s00170-017-0032-8.

[12] SHIH Y P, FONG Z H. Flank correction for spiral bevel and hypoid gears on a six-axis CNC hypoid generator [J]. Journal of Mechanical Design, 2008, 130(6): 062604. DOI: 10.1115/1.2890112.

[13] JIANG Jin-ke, FANG Zong-de. High-order tooth flank correction for a helical gear on a six-axis CNC hob machine [J]. Mechanism and Machine Theory, 2015, 91(9): 227-237. DOI: 10.1016/j.mechmachtheory.2015.04.012.

[14] LIN C Y, TSAY C B, FONG Z H. Computer-aided manufacturing of spiral bevel and hypoid gears with minimum surface-deviation [J]. Mechanism and Machine Theory, 1998, 33(6): 785-803. DOI: 10.1016/s0094-114x(97)00101-8.

[15] CHEN Shu-han, YAN Hong-zhi. Research on tooth surface deviation correction algorithm of spiral bevel gear based on tilting method [J]. Chinese Mechanical Engineering, 2011, 22(9): 1080-1084. DOI: 10.1631/jzus.A1000257. (in Chinese)

[16] MING Xing-zu, FANG Shu-guang, WANG Hong-yang. Tooth surface form correction for face gear grinding [J]. China Mechanical Engineering, 2018, 29(17): 2031-2037. DOI: 10.3969/j.issn.1004-132X.2018.17.003. (in Chinese)

[17] ARTONI A, GABICCINI M, KOLIVAND M. Ease-off based compensation of tooth surface deviations for spiral bevel and hypoid gears: Only the pinion needs corrections [J]. Mechanism and Machine Theory, 2013, 61(3): 84-101. DOI: 10.1016/j.mechmachtheory.2012.10.005.

[18] DING Hang, TANG Jin-yuan, ZHONG J. An accurate model of high-performance manufacturing spiral bevel and hypoid gears based on machine setting modification [J]. Journal of Manufacturing Systems, 2016, 41: 111-119. DOI: 10.1016/j.jmsy.2016.08.004.

[19] DING Han, WAN Guo-xin, ZHOU Yuan-sheng, TANG Jin-yuan, ZHOU Zhen-yu. Nonlinearity analysis based algorithm for indentifying machine settings in the tooth flank topography correction for hypoid gears [J]. Mechanism and Machine Theory, 2017, 113: 1-21. DOI: 10.1016/ j.mechmachtheory.2017.02.007.

[20] ZHANG Yu, YAN Hong-zhi, ZENG Tao, ZENG Yi-yu. Tooth surface geometry optimization of spiral bevel and hypoid gears generated by duplex helical method with circular profile blade [J]. Journal of Central South University, 2016, 23(3): 544-554. DOI: 10.1007/s11771-016-3101-5.

[21] LITVIN F L, FUENTES A, HAYASAKA K. Design, manufacture, stress analysis, and experimental tests of low-noise high endurance spiral bevel gears [J]. Mechanism and Machine Theory, 2006, 41(1): 83-118. DOI: 10.1016/ j.mechmachtheory.2005.03.001.

[22] DENG Jing, JIANG Chuang, DENG Xiao-zhong, ZHANG Ming-zhu, NIE Shao-wu. The optimal calculation and machining of the spiral bevel gear pinion based on the same cutter head [J]. Journal of Advanced Mechanical Design Systems and Manufacturing, 2020, 14(4): 1-16. DOI: 10.1299/jamdsm.2020jamdsm0045.

[23] MU Yan-ming, LI Wen-li, FANG Zong-de, ZHANG Xi-jin. A novel tooth surface modification method for spiral bevel gears with higher-order transmission error [J]. Mechanism and Machine Theory, 2018, 126(8): 49-60. DOI: 10.1016/ j.mechmachtheory.2018.04.001.

[24] PENG Shan-dong, DING Han, TANG Jin-yuan, ZHOU Yuan-sheng. Collaborative machine tool settings compensation considering both tooth flank geometrical and physical performances for spiral bevel and hypoid gears [J]. Journal of Manufacturing Processes, 2020, 54(6): 169-179. DOI: 10.1016/j.jmapro.2020.02.035.

[25] VIVET M, TAMAROZZI T, DESMET W, MUNDO D. On the modelling of gear alignment errors in the tooth contact analysis of spiral bevel gears [J]. Mechanism and Machine Theory, 2021, 155(1): 104065. DOI: 10.1016/ j.mechmachtheory.2020.104065.

[26] MU Yan-ming, LI Wen-li, FANG Zong-de. Tooth surface modification method of face-milling spiral bevel gears with high contact ratio based on cutter blade profile correction [J]. International Journal of Advanced Manufacturing Technology 2020, 106(7): 3229-3237. DOI: 10.1007/s00170-019-04738-3.

[27] ARTONI A, GABICCINI M, GUIGGIANI M. Nonlinear identification of machine settings for flank form modifications in hypoid gears [J]. Journal of Mechanical Design, 2008, 130(11): 112602. DOI: 10.1115/1.2976454.

[28] ZHAO Ying-liang, XU Cheng-xian. Tangent single dogleg method for trust region subproblems [J]. Journal on Numerical Methods and Computer Applications, 2000, 21(1): 77-80. (in Chinese)

[29] ZHANG Yu, YAN Hong-zhi. Tooth surface error correction methodologies for spiral bevel and hypoid gears generated by duplex helical method [C]// 2019 International Conference on Advances in Construction Machinery and Vehicle Engineering (ICACMVE). Changsha, China, 2019: 362-368. DOI: 10.1109/ICACMVE.2019.0007.

(Edited by FANG Jing-hua)

中文导读

双螺旋法切削准双曲面齿轮的齿面误差修正

摘要：本文研究了双重螺旋法同步切削准双曲面齿轮凹凸两面的齿面误差修正问题。首先，建立了双重螺旋法切削准双曲面齿轮的数学模型；其次，通过测量中心得到齿面离散点的坐标，计算离散点的法向误差；第三，建立了齿面误差修正模型，并采用含信赖域策略的Levenberg-Marquard算法和最小二乘法对齿面误差进行修正；最后，利用对齿面误差的修正效果更好的含信赖域策略的Levenberg-Marquard算法得到的加工参数对齿面进行磨削实验。实验结果表明，对齿面误差进行修正后，最大绝对误差从初始的30.9 μm降低为6.8 μm，凹面误差均方根从初始的15.1 μm降低为2.1 μm，凸面误差均方根从10.8 μm降低为1.8 μm，凹凸两面误差平方和从初始的15471 μm²降低为358 μm²。验证了含信赖域策略的Levenberg-Marquard算法对双螺旋法切削准双曲面齿轮的齿面误差修正具有良好的精度。

关键词：双重螺旋法；准双曲面齿轮；误差测量；含信赖域策略的Levenberg-Marquard算法；齿面误差修正

Foundation item: Projects(52075552, 51575533, 51805555, 11662004) supported by the National Natural Science Foundation of China

Received date: 2020-06-16; Accepted date: 2020-11-27

Corresponding author: YAN Hong-zhi, PhD, Professor; Tel: +86-13637315291; E-mail: yhzcsu@csu.edu.cn; ORCID: https://orcid.org/ 0000-0003-4144-5279