DOI: 10.11817/j.issn.1672-7207.2019.05.025
高应力泥质粉砂岩黏弹塑性蠕变模型
刘新喜1,2,李盛南1,2,徐泽佩1,2,李玉1,2,高学文1,王玮玮1
(1. 长沙理工大学 土木工程学院,湖南 长沙,410114;
2. 桥梁结构安全控制湖南省工程实验室,湖南 长沙,410114)
摘要:为揭示高应力作用下深埋硐室围岩的流变特性,采用分级增量加载方式对泥质粉砂岩进行三轴压缩蠕变实验,根据稳态蠕变速率与应力的关系,利用给定蠕变速率阈值确定岩石的长期强度;结合蠕变曲线特征,将瞬弹性、黏弹性、黏塑性应变分离,建立模型各参数与应力和时间的函数关系;根据损伤定义确定瞬弹性、黏弹性元件的损伤变量,并引入瞬弹性、黏弹性损伤变量和黏塑性修正系数对西原模型进行优化,提出一种可以描述高应力作用下岩石蠕变全过程的变参数模型。研究结果表明:稳态蠕变速率随应力增大呈指数增大,采用给定蠕变速率阈值求得岩石的长期强度为68.82 MPa,为单轴抗压强度的74.80%;基于黏弹塑性应变分离建立的蠕变模型能够很好地描述岩石蠕变全过程的非线性特征,且优化模型与实验数据拟合较好,证明了该蠕变模型的合理性。
关键词:岩石力学;泥质粉砂岩;蠕变实验;蠕变模型;非线性
中图分类号:U416 文献标志码:A 文章编号:1672-7207(2019)05-1210-11
Viscoelastic-plastic creep model of high stress argillaceous siltstone
LIU Xinxi1, 2, LI Shengnan1, 2, XU Zepei1, 2, LI Yu1, 2, GAO Xuewen1, WANG Weiwei1
(1. School of Civil Engineering Changsha University of Science and Technology, Changsha 410114, China;
2. Hunan Province Engineering Laboratory of Bridge Structure Changsha University of Science & Technology,Changsha 410114, China)
Abstract: In order to reveal the rheological characteristics of deep buried underground chamber surrounding rock under high stress, triaxial compression creep test was carried out on argillaceous siltstone by incremental loading method. According to the relationship between steady-state creep rate and stress, the long-term strength of rock was determined by using a given creep rate threshold. Considering the characteristics of creep curve, the function relationship among the parameters of model, stress level and time was established based on separation of instantaneous elasticity viscoelastic, and viscoplastic strain from creep curves. According to the damage definition, the damage variables of instantaneous elastic element and viscoelastic element were determined, and the Nishihara model was optimized by introducing instantaneous elasticity, viscoelastic damage variable and viscoplastic correction coefficient, which could describe the whole process of rock creep under high stress. The results show that the steady creep rate increases exponentially with the increase of stress. The long-term strength of rock obtained by the given creep rate threshold is 68.82 MPa, which is 74.80% of the uniaxial compressive strength. The creep model established based on strain viscoelastic-plastic separation can well describe the nonlinear characteristics of the whole process of rock creep, and the fitting between the optimized model and the experimental data is good, which proves the rationality of the creep model.
Key words: rock mechanics; argillaceous siltstone; creep test; creep model; nonlinear
在高应力作用下,深埋硐室流变破坏问题已严重影响我国地下工程的建设[1-2]。在深埋硐室二次衬砌施工完成后,由于衬砌刚度较大,围岩和支护结构处于暂时稳定状态。但在高地应力长期作用下,围岩内部结构不断调整重组,使得围岩蠕变持续发展,承载能力下降,进而导致围岩破坏和支护结构失效[3]。研究高应力作用下岩石的蠕变特性对深埋硐室支护设计和长期稳定性评价具有重要意义。岩石在高应力作用下的蠕变具有明显非线特征[4-6],而以往的研究大多基于元件理论,通过线性元件Hooke体、St.Venant体、Newton体串联或并联组合模型来描述岩石蠕变的弹性、黏弹性、黏塑性等特性,该方法建立的模型具有严格的理论意义,但模型均由线性元件组合,得到的本构关系不能反映岩石蠕变的非线性特征[7]。近年来,许多学者在元件理论的基础上,通过引入非线性元件来改进模型,使得模型在加速蠕变过程具有非线性特征,并通过数值拟合对模型参数进行识别,建立了岩石蠕变的变参数模型。如王军保等[8]采用一种黏滞系数随应力和时间变化的非线性黏滞元件,将之与经典的弹性、黏性元件组合,建立了可以反映岩石蠕变非线性特征的模型。张治亮等[9]提出了能够反映不同围压下岩石加速启动时间的非线性元件,并与Burgers模型组合,建立了岩石在不同围岩下的非线性黏弹塑性蠕变模型。高赛红等[10]针对高应力作用下岩石蠕变的非线性特征,提出将瞬时Hooke体、瞬时塑性、村山体和非线性黏塑体组合,建立了能够描述岩石蠕变全过程特征的非线性模型。康永刚等[11]将Burgers模型中的牛顿黏壶元件改进为与应力水平和时间相关的变量,改进的模型能描述岩石蠕变的全过程。齐亚静等[12]针对传统的西原模型难以描述岩石非线性流变特性的问题,提出了一个带应变触发的非线性塑性元件与西原模型串联,改进的模型能很好地反映岩石加速蠕变的非线性特征。LI等[13]通过将Burgers模型与塑性元件串联,提出一种能描述层状复合岩石蠕变特性的新模型。蒋海飞等[14]在Burgers模型上串联1个非线性黏性元件,所建立的模型能够描述高围压高水压条件下岩石的加速蠕变。赵宝云等[15]通过Kelvin体与非线性黏塑性元件串联,提出了一种描述短时蠕变的非线性蠕变模型。上述对岩石蠕变模型非线性特征的研究大多集中在加速蠕变阶段,只考虑了模型中黏滞系数随时间和应力的变化影响,而已有研究表明高应力作用下岩石的非线性特征贯穿岩石整个蠕变过程,模型中各参数均应视为变量。对此,刘新喜等[16]在Burgers模型的基础上,基于损伤理论建立了模型各参数随时间和应力变化的损伤方程,提出了高应力作用下岩石非线性蠕变损伤模型,并具有较好的拟合效果。但模型中各参数仅通过蠕变曲线整体拟合自动识别,得到的模型参数变化规律很难客观反映蠕变各阶段弹性和塑性蠕变的真实变化规律。针对上述研究的不足,本文作者在对泥质粉砂岩进行三轴压缩蠕变实验的基础上,根据稳定蠕变速率与应力的关系,采用给定蠕变速率阈值确定岩石的长期强度;结合岩石蠕变曲线特征,以长期强度为黏塑性蠕变的应力阈值,分别对瞬弹性、黏弹性、黏塑性应变进行分析,并通过数值拟合建立各个蠕变参数与应力和时间的函数关系,引入损伤方程和黏塑性修正系数对模型进行优化,提出一种可以描述高应力作用下岩石蠕变的变参数模型,可望为深埋硐室围岩支护设计和长期稳定性评价提供参考。
1 蠕变实验
1.1 试样制备及实验过程
在某深埋硐室施工现场选取新开挖的泥质粉砂完整岩块,利用ZS-100岩石钻芯取样机垂直岩块层理进行取芯,取芯方法采用水钻法;利用SHM-200双端面打磨机对切割完好芯样进行打磨,制备成直径×高为50 mm×100 mm的圆柱体标准试件,控制径向误差不大于0.5 mm。制备好的试样见图1(a)。采用RLW-2000三轴流变实验仪器进行三轴流变实验,实验装置见图1(b)。为模拟岩石的高地应力,设定围压为20 MPa。实验加载方式为分级增量加载,根据泥质粉砂岩单轴抗压强度92.0 MPa,从30~100 MPa分为8级加载,应力加载速率为0.1~0.3 MPa/s,每一级加载应力持续48 h以上。当轴向应变小于0.001 d-1时,可认为岩石蠕变速率不再发生改变,即岩石处于稳定状态,然后进行下一级加载,直至岩石试样被破坏为止。
1.2 实验结果
泥质粉砂岩在各级应力作用下的蠕变曲线见图2。从图2可见:岩石蠕变曲线具有明显非线性特征,在各级应力作用下,岩石均出现瞬弹应变和衰减蠕变;在较低应力(小于60 MPa)作用下,岩石蠕变速率逐渐减小,并趋近于0 h-1,岩石只出现衰减蠕变;在较高应力时(70~90 MPa),岩石蠕变速率随时间减小,最终保持稳定,进入定常蠕变阶段;当应力大于单轴抗压强度(大于92.0 MPa时),岩石经历短暂的稳定蠕变,很快就发生加速蠕变破坏。

图1 实验试样及仪器
Fig. 1 Test sample and apparatus
高应力作用下岩石的蠕变全过程曲线见图3。由图3可知:
 (1)
(1)
 (2)
(2)
其中: ,
, 和
和 分别为总应变、瞬时应变和阶段蠕变;
分别为总应变、瞬时应变和阶段蠕变; ,
, 和
和 分别为衰减蠕变阶段、定常蠕变阶段和加速蠕变阶段的蠕变。
分别为衰减蠕变阶段、定常蠕变阶段和加速蠕变阶段的蠕变。

图2 各级应力作用下泥质粉砂岩的蠕变曲线
Fig. 2 Creep curves of argillaceous siltstone under different grading stresses

图3 高应力作用下岩石的全蠕变曲线
Fig. 3 Full creep curve of rock under high stress
根据全蠕变曲线得到蠕变各阶段的应变见表1。从表1可见:总应变、瞬时应变和总蠕变均随应力增大而增大;瞬时应变占总应变量的70%以上,说明岩石变形绝大部分在加载瞬时产生;岩石蠕变破坏前(应力≤90 MPa),衰减蠕变阶段和定常蠕变阶段的蠕变均随应力增加而增大,蠕变主要在衰减蠕变阶段产生,但蠕变仅为单轴破坏时极限应变( =3.51×10-3)的3.77%~12.03%;当应力为100 MPa时,岩石蠕变主要在加速蠕变阶段产生,蠕变随着时间迅速增大,直至岩石被破坏。因此,在高应力作用下,岩石加速蠕变是导致深埋硐室围岩失稳破坏的主要原因。
=3.51×10-3)的3.77%~12.03%;当应力为100 MPa时,岩石蠕变主要在加速蠕变阶段产生,蠕变随着时间迅速增大,直至岩石被破坏。因此,在高应力作用下,岩石加速蠕变是导致深埋硐室围岩失稳破坏的主要原因。
表1 蠕变各阶段的应变
Table 1 Strain of creep under different grading stages

2 长期强度
长期强度是岩石进入加速蠕变的应力阈值,即为蠕变由稳定状态向加速状态发展的拐点。确定岩石长期强度的方法主要有直接法和间接法。由于采用直接法需要进行大量实验,持续时间较长,目前多采用间接法,其包括等时曲线法和过渡蠕变法等[17]。等时曲线的拐点具有多变性,该方法用于确定岩石长期强度的准确性还需进一步探讨[18];过渡蠕变法需要确定蠕变速率为零的最大荷载,在实验过程中受实验装置及外界环境影响,一般很难得到[19]。采用给定蠕变速率阈值作为岩石蠕变拐点,能降低确定岩石长期强度的难度,往往能取得较好的效果。为消除衰减蠕变阶段的影响,准确求得稳态蠕变阶段的蠕变速率,取各级应力蠕变20 h后的稳态蠕变曲线进行拟合,得到各级应力作用下的稳态蠕变速率见表2。
表2 各应力状态下稳态蠕变速率
Table 2 Steady state creep rate under grading stress states

稳态蠕变速率与应力的关系曲线见图4。各级应力作用下岩石稳态蠕变速率并不为0 h-1,岩石稳定蠕变速率随应力呈指数增加;当应力小于60 MPa时,岩石的稳态蠕变速率变化较小((5.052~19.329)×10-8 h-1);当应力大于60 MPa时,岩石的稳态蠕变速率迅速增大。稳定蠕变速率v与加载应力σ的拟合关系式为

图4 各级应力作用下稳定蠕变阶段的蠕变速率
Fig. 4 Creep rate of stable creep stage under different grading stresses
v=5.147 2×10-8+1.078 6×10-9×exp(0.096 8σ), R2=0.985 (3)
岩石的蠕变速率可反映岩石的损伤状态,岩石在较低应力作用下,岩石硬化效应强于损伤效应,岩石颗粒体间的裂隙随颗粒结构调整重组而发生闭合,岩石蠕变速率逐渐减小;当应力超过某一阈值时,损伤效应强于硬化效应,岩石颗粒体胶结状态不断发生破坏,导致裂隙开展,内部损伤不断积累,岩石蠕变速率保持稳定;随着应力进一步加大,岩石局部发生破坏,导致岩石有效承载面积减小,损伤从局部向周边发展,岩石加速蠕变破坏,蠕变速率快速增大。可见,岩石蠕变速率保持稳定阶段,虽然岩石损伤积累,但能保持较长时间的稳定状态。岩石裂隙开展及颗粒体流动均具有随机性,只要岩石能保持较长时间的稳定即可认为岩石不发生蠕变破坏,可取岩石蠕变破坏前平均累计损伤效应为岩石局部破坏限值;当岩石有效承载面积大于破坏前平均有效承载承载面积时可保持相对稳定。从稳态蠕变速率考虑,可取岩石破坏前的平均稳态蠕变速率为岩石破坏的速率阈值。稳态蠕变速率小于岩石破坏的速率阈值即岩石保持相对稳定,破坏前的平均稳态蠕变速率 可表示为
可表示为
 (4)
(4)
式中: 为第i级加载作用下的稳态蠕变速率;n为破坏前总的加载级数。求得破坏前的平均稳态蠕变速率
为第i级加载作用下的稳态蠕变速率;n为破坏前总的加载级数。求得破坏前的平均稳态蠕变速率 =1.023×10-6 h-1,将其作为速率阈值代入式(3)可求得其对应的应力阈值即岩石的长期强度为68.82 MPa,为单轴抗压强度的74.80%,这与SZCZEPANIK等[20]得出的岩石长期强度为单轴抗压强度的70%~80%的结论相符。
=1.023×10-6 h-1,将其作为速率阈值代入式(3)可求得其对应的应力阈值即岩石的长期强度为68.82 MPa,为单轴抗压强度的74.80%,这与SZCZEPANIK等[20]得出的岩石长期强度为单轴抗压强度的70%~80%的结论相符。
3 蠕变模型
在高应力作用下,泥质粉砂岩蠕变具有明显应力阈值即岩石的长期强度。当应力小于阈值时,岩石硬化效应强于损伤效应,颗粒间胶结物受外力作用产生的裂隙随岩石颗粒体流动逐渐闭合;外力撤销后,颗粒体的变形可立即恢复,颗粒间相对位移随时间缓慢恢复,在宏观上表现出岩石蠕变的瞬弹和黏弹性特征。当应力大于阈值时,岩石损伤效应强于硬化效应,在外力作用下岩石颗粒体间裂隙逐渐开展,进而导致岩石颗粒体局部破坏。当外力撤销时,颗粒体的变形可立即恢复,而颗粒间胶结物未破坏部分随时间逐渐恢复,破坏部分不能恢复,在宏观上表现出岩石蠕变的瞬弹性、黏弹性和黏塑性特征[21-22]。结合蠕变曲线特征分析,岩石的蠕变模型可由Hooke体、Kelvin体和Bingham体组成。传统的西原模型能很好描述岩石黏弹塑性特征,且能反映岩石加速蠕变时的应力阈值,其模型组成元件如图5所示,模型方程见式(5)。

图5 西原模型
Fig. 5 Nishihara model
 (5)
(5)
式中:E0为瞬时变形模量;Ece为黏弹性变形模量;ηce为黏弹性黏滞系数;ηdc为黏塑性黏滞系数;σs为长期强度。该模型均由线性元件组成,当应力超过应力阈值时,颗粒体的胶结状态发生破坏,颗粒体间的黏滞流动并非线性。为此,本文在西原模型的基础上,以长期强度为黏塑性应变的应力阈值,将岩石蠕变的瞬弹性、黏弹性和黏塑性蠕变分离,通过数值拟合工具分别对其蠕变参数进行识别,建立瞬弹性、黏弹性和黏塑性蠕变参数与应力和时间的函数关系,并引入参数修正变量对西原模型进行优化,即可得到高应力泥质粉砂岩蠕变全过程的变参数模型。
3.1 瞬时变形模量
瞬时变形模量是指荷载作用时间t趋于0时,应力增量 与应变增量
与应变增量 的比值。岩石蠕变的瞬时变形模量E0可表示为:
的比值。岩石蠕变的瞬时变形模量E0可表示为:
 (6)
(6)
 (7)
(7)
式中: 和
和 分别为第i级加载下时间t趋于0时蠕变应力增量和应变增量;i为大于1的整数。
分别为第i级加载下时间t趋于0时蠕变应力增量和应变增量;i为大于1的整数。
求得各级应力作用下岩石的瞬时变形模量见图6。从图6可见,岩石瞬时变形模量随应力增加而减小。通过数值拟合得到各级应力作用的瞬时变形模量表达式:
 (8)
(8)
其中:E(0,i)为第i级加载的瞬时变形模量;σi为加载应力。

图6 瞬时变形模量与应力的关系
Fig. 6 Relationship between instantaneous deformation modulus and stress
岩石是多相复合结构材料,在成岩过程中,因长期的地质运动,内部存在大量的节理裂隙。由于深埋硐室围岩长期在高应力作用下内部裂隙被挤密压实,当围岩被开挖出来时,应力突然释放使得岩石裂隙开展造成岩体损伤。进行岩石蠕变实验时,瞬时加载过程使得岩石损伤进一步加剧。根据损伤定义可得岩石初始损伤变量D(0,i)为
 (9)
(9)
式中: 39.385 6 GPa;a0=9.972×10-5;b0=7.587×10-2;R2= 0.986。
39.385 6 GPa;a0=9.972×10-5;b0=7.587×10-2;R2= 0.986。
3.2 黏弹变形模量
当应力小于长期强度时,岩石衰减蠕变见图7,可见岩石蠕变速率逐渐减小趋于0 h-1,蠕变主要由瞬弹性、黏弹性蠕变组成。岩石黏弹蠕变εce可由下式进行计算:
 (10)
(10)
当应力小于长期强度时,各级应力的黏弹性应变 见图8。
见图8。

图7 应力小于长期强度的衰减阶段应变
Fig. 7 Attenuation stage strain when stress is smaller than long-term strength

图8 应力小于长期强度的黏弹性应变
Fig. 8 Attenuation stage viscoelastic strain when stress is less than long-term strength
岩石蠕变可用Kelvin体来拟合黏弹性应变,通过拟合参数见表3。
 (11)
(11)
其中: 为t→∞的黏弹性应变。
为t→∞的黏弹性应变。
表3中, 和
和 是与应力有关的函数,通过最小二乘法拟合得到:
是与应力有关的函数,通过最小二乘法拟合得到:
 ×
× ×
× (12)
(12)
 (13)
(13)
根据Kelvin体本构方程
 (14)
(14)
蠕变速率 可由下式计算:
可由下式计算:
 (15)
(15)
通过计算得到岩石蠕变速率见图9。
表3 黏弹性蠕变拟合参数
Table 3 Viscoelastic creep fitting parameters


图9 应力小于长期强度的黏弹性应变速率
Fig. 9 Viscoelastic strain rate when stress is less than long-term strength
将 代入式(14)可得
代入式(14)可得
 (16)
(16)
求得黏弹性变形模量如图10所示。
利用最小二乘法对黏弹性变形模量进行拟合可得
 (17)
(17)
各级应力岩石黏弹性变形模量的参数见表4。
岩石黏弹性变形模量拟合参数是与应力有关的参数,通过拟合得到拟合参数与应力的关系:

图10 应力小于长期强度时的黏弹性变形模量
Fig. 10 Viscoelastic deformation modulus when stress is less than long-term strength
表4 应力小于长期强度时黏弹性变形模量拟合参数
Table 4 Fitting parameters of viscoelastic deformation modulus when stress is less than long-term strength

 ×
× (18)
(18)
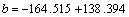 ×
× (19)
(19)
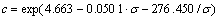 (20)
(20)
根据式(18),(19)和(20)计算当应力大于长期强度时黏弹性变形模量的相关参数见表5。将表5中各参数代入式(17)即可得当应力大于长期强度时各级应力的黏弹性变形模量,见图11。
将式(13)和式(16)代入式 ,可求得黏弹黏性滞系数
,可求得黏弹黏性滞系数 ,见图12。
,见图12。
表5 应力大于长期强度时黏弹性变形模量拟合参数
Table 5 Fitting parameters of viscoelastic deformation modulus when stress is larger than long-term strength


图11 应力大于长期强度时的黏弹性变形模量
Fig.11 Viscoelastic deformation modulus when stress is greater than long-term strength

图12 各级应力的黏弹性黏滞系数
Fig. 12 Viscoelastic viscosity coefficient under different stress levels
从图10~12可知:岩石黏弹性变形模量和黏弹性黏滞系数均随时间增加而减小,最终趋于稳定,应力越大,保持稳定需要的时间越长。从岩石损伤角度看,岩石在外力作用下岩石颗粒体间产生细小裂隙,但随着颗粒体定向流动,微裂隙逐渐发生闭合,使得岩石损伤得到抑制,表现出岩石应变速率随时间逐渐减小;当颗粒体定向排列稳定时,岩石应变速率趋近于0;应力越大,颗粒体硬化流动时间越长,蠕变稳定需要的时间就越长。
根据损伤定义,岩石黏弹性变形模量损伤因子W和黏弹性黏滞系数损伤因子ξ可表示为:
 (21)
(21)
 (22)
(22)
岩石的黏弹性变形模量和黏弹性黏滞系数的损伤因子与时间的关系分别见图13和图14。

图13 黏弹性变形模量损伤因子与时间的关系
Fig. 13 Relationship between damage factor of viscoelastic deformation modulus and time
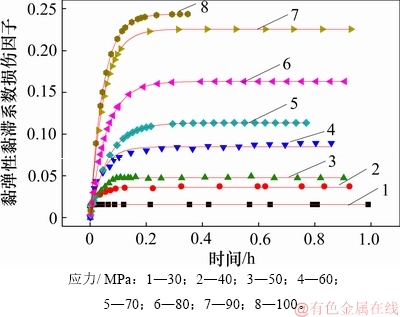
图14 黏弹性黏滞系数损伤因子与时间的关系
Fig. 14 Relationship between damage factor of viscoelastic viscosity coefficient and time
黏弹性变形模量和黏滞系数的损伤因子可由下式进行拟合:
 (23)
(23)
 (24)
(24)
式(23)和式(24)的拟合参数aw,bw, ,
, 见表6。
见表6。
3.3 黏塑性黏滞系数
当应力大于长期强度时,岩石颗粒体间的胶结状态发生破坏,颗粒体定向流动并不能完全使裂隙闭 合;随着时间增加,颗粒体间的裂隙持续发展,岩石蠕变速率保持稳定,岩石损伤不断积累,颗粒体破坏状态从局部向周边发展,使得岩石黏塑性变形积累;随着裂隙开展,岩石有效承载面积减小,最终岩石发生破坏。黏塑性变形εdc可由下式进行计算:
 (25)
(25)
计算得到的应力大于长期强度的黏塑性应变见图15。
表6 黏弹性变形模量和黏滞系数损伤因子拟合参数
Table 6 Fitting parameters of viscoelastic deformation modulus and viscoelastic damage factor

从图15可知:在高应力作用下,岩石的黏塑性应变在整个蠕变过程均存在,并不仅仅存在于加速蠕变阶段,高赛红等[10]认为岩石蠕变过程实质是硬化效应和损伤效应相互作用的结果,损伤效应积累导致岩石塑性蠕变发展,从而塑性蠕变贯穿整个蠕变过程;若仅仅在加速蠕变阶段考虑岩石的塑性蠕变,而在衰减阶段则直接利用低应力作用下黏弹性模型,势必会导致岩石衰减阶段的蠕变误差较大;同时,通过参数整体拟合得到的加速蠕变模型参数与实际参数存在差异。因此,本文将瞬弹性、黏弹性、黏塑性应变分开进行拟合,不仅能充分考虑衰减蠕变阶段的黏塑性应变,而且可得到加速蠕变阶段更为真实参数变化规律,由此建立的蠕变模型能更好地反映岩石蠕变的非线性特征。
岩石黏塑性蠕变可以采用幂律型函数式(26)进行拟合,拟合的相关参数见表7。
 (26)
(26)
由于岩石在加速蠕变阶段,颗粒体间的联结强度减弱,岩石软化效应增强,导致颗粒体大量定向排列和面-面接触使得黏结能力减弱,颗粒流变速率的规律性减弱[22]。所以,黏塑性应变拟合相关性相对于黏弹性阶段较差。
由此可得岩石黏塑性黏滞系数ηdc(σ, t)计算式为
 (27)
(27)

图15 各级应力作用下的黏塑性应变
Fig. 15 Viscoplastic strain under different stresses
表7 黏塑性应变拟合参数
Table 7 Fitting parameters of viscoplastic strain

4 优化模型及验证
分别对高应力作用下岩石蠕变瞬弹、黏弹、黏塑性应变进行分析,建立瞬弹、黏弹性变形模量的损伤因子和黏塑性黏滞系数函数,引入修正变量对模型进行优化。改进的模型见图16,模型方程为

图16 改进的模型
Fig. 16 Improved model
 (28)
(28)
其中:E0为瞬时变形模量;D0为瞬时变形模量损伤因子, ×
× ;Ece为黏弹性变形模量;w为黏弹性变形模量损伤因子,w=aw×[1-exp(bw·t)];ηce为黏弹性黏滞系数;ξ为黏弹性黏滞系数损伤因 子,
;Ece为黏弹性变形模量;w为黏弹性变形模量损伤因子,w=aw×[1-exp(bw·t)];ηce为黏弹性黏滞系数;ξ为黏弹性黏滞系数损伤因 子,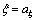 ×
× ;ηdc为黏塑性黏滞函数,
;ηdc为黏塑性黏滞函数, 。
。
通过式(28)对各级应力的蠕变实验结果进行拟合,部分拟合曲线见图17,从图17可知:各级应力作用下优化模型与实验结果拟合较好,优化的模型能很好地反映岩石蠕变全过程的非线性特征,可为深埋硐室设计和施工提供参考。

图17 蠕变模型拟合曲线
Fig. 17 Fitting curve of creep model
5 结论
1) 采用岩石蠕变破坏前的稳态蠕变速率平均值作为速率阈值,并结合稳态蠕变速率与应力水平的函数关系,得到岩石的长期强度为68.82 MPa,为单轴抗压强度的74.80%;由该方法推测岩石长期强度比较简单,可为确定岩石长期强度提供参考。
2) 通过将蠕变曲线中黏弹性、黏塑性应变进行分析,发现高应力作用下泥质粉砂的衰减蠕变阶段具有黏弹塑性特征,黏塑性应变随时间和应力非线性增大,故研究高应力作用下岩石蠕变非线性特征应考虑衰减阶段塑性变形的影响。
3) 根据损伤定义,建立了岩石瞬弹性、黏弹性参数的损伤方程和黏塑性黏滞系数函数,引入修正变量的蠕变模型能很好反映高应力作用下岩石蠕变全过程的非线性特征。
参考文献:
[1] 王路军, 周宏伟, 荣腾龙, 等. 深部煤体非线性蠕变本构模型及实验研究[J]. 煤炭学报, 2018, 43(8): 2196-2203.
WANG Lujun, ZHOU Hongwei, RONG Tenglong, et al. Research on Experimental and nonlinear creep constitutive model of coal at depth[J]. Journal of China Coal Society, 2018, 43(8): 2196-2203.
[2] 王更峰. 炭质板岩蠕变特性研究及其在隧道变形控制中的应用[D]. 重庆: 重庆大学土木工程学院, 2012: 6-8.
WANG Gengfeng. Creep characteristics of carbonaceous slate and its application in tunnel deformation control[D]. Chongqing: Chongqing University. School of Civil Engineering, 2012: 6-8.
[3] 汪斌, 朱杰兵, 邬爱清, 等. 高应力下岩石非线性强度特性的实验验证[J]. 岩石力学与工程学报, 2010, 29(3): 542-548.
WANG Bin, ZHU Jiebing, WU Aiqing, et al. Experimental verification of rock nonlinear strength characteristics under high stress[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(3): 542-548.
[4] 朱杰兵. 高应力下岩石卸荷及其流变特性研究[D]. 武汉: 中国科学院研究生院(武汉岩土力学研究所), 2009: 84-88.
ZHU Jiebing. Study on unloading and rheological properties of rock under high stress[D]. Wuhan: Graduate School of Chinese Academy of Sciences(Wuhan Institute of Geotechnical Mechanics), 2009: 84-88.
[5] 昝月稳, 俞茂宏, 赵坚, 等. 高应力状态下岩石非线性统一强度理论[J]. 岩石力学与工程学报, 2004, 23(13): 2143-2148.
ZAN Yuewen, YU Maohong, ZHAO Jian, et al. Rock nonlinear unified strength theory under high stress state[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(13): 2143-2148.
[6] 杨文东, 张强勇, 陈芳, 等. 辉绿岩非线性流变模型及蠕变加载历史的处理方法研究[J]. 岩石力学与工程学报, 2011, 30(7): 1405-1413.
YANG Wendong, ZHANG Qiangyong, CHEN Fang, et al. Research on nonlinear rheological model of diabase and treatment for creep loading history[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(7): 1405-1413.
[7] 宋勇军, 雷胜友, 韩铁林. 一种新的岩石非线性黏弹塑性流变模型[J]. 岩土力学, 2012, 33(7): 2076-2080.
SONG Yongjun, LEI Shengyou, HAN Tielin. A new nonlinear viscoelasto-plastic rheological model for rocks[J]. Rock and Soil Mechanics, 2012, 33(7): 2076-2080.
[8] 王军保, 刘新荣, 王铁行. 基于改进分数阶黏滞体的岩石非线性蠕变模型[J]. 中南大学学报(自然科学版), 2015, 46(4): 1461-1467.
WANG Junbao, LIU Xinrong, WANG Tiehang. A nonlinear creep model for rocks based on modified fractional viscous body[J]. Journal of Central South University(Science and Technology), 2015, 46(4): 1461-1467.
[9] 张治亮, 徐卫亚, 王伟. 向家坝水电站坝基挤压带岩石三轴蠕变实验及非线性黏弹塑性蠕变模型研究[J]. 岩石力学与工程学报, 2011, 30(1): 132-140.
ZHANG Zhiliang, XU Weiya, WANG Wei. Triaxial creep test and nonlinear viscoelastic-plastic creep model of rock in compression zone of Xiangjiaba Hydropower Station[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(1): 132-140.
[10] 高赛红, 曹平, 汪胜莲, 等. 改进的岩石非线性黏弹塑性蠕变模型及其硬化黏滞系数的修正[J]. 煤炭学报, 2012, 37(6): 936-943.
GAO Saihong, CAO Ping, WANG Shenglian, et al. Improved rock nonlinear viscoelastic plastic creep model and correction of hardening viscosity coefficient[J]. Journal of China Coal Society, 2012, 37(6): 936-943.
[11] 康永刚, 张秀娥. 一种改进的岩石蠕变本构模型[J]. 岩土力学, 2014, 35(4): 1049-1055.
KANG Yonggang, ZHANG Xiue. An improved constitutive model of rock creep[J]. Rock and Soil Mechanical, 2014, 35(4): 1049-1055.
[12] 齐亚静, 姜清辉, 王志俭, 等. 改进西原模型的三维蠕变本构方程及其参数辨识[J]. 岩石力学与工程学报, 2012, 31(2): 347-355.
QI Yajing, JIANG Qinghui, WANG Zhijian, et al. The improvement of the three-dimensional creep constitutive equation and its parameter identification of the Xiyuan model[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 347-355.
[13] LI Wenquan, LI Xiangdong, HAN Bing, et al. Recognition of creep model of layer composite rock mass and its application[J]. Journal of Central South University of Technology, 2007, 14(1): 329-331.
[14] 蒋海飞, 刘东燕, 赵宝云, 等. 高围压高水压条件下岩石非线性蠕变本构模型[J]. 采矿与安全工程学报, 2014, 31(2): 284-291.
JIANG Haifei, LIU Dongyan, ZHAO Baoyun, et al. Nonlinear creep constitutive model of rock under high confining pressure and high water pressure[J]. Journal of Mining & Safety Engineering, 2014, 31(2): 284-291.
[15] 赵宝云, 刘东燕, 郑志明, 等. 基于短时三轴蠕变实验的岩石非线性黏弹塑性蠕变模型研究[J]. 采矿与安全工程学报, 2011, 28(3): 446-451.
ZHAO Baoyun, LIU Dongyan, ZHENG Zhiming, et al. Study on nonlinear viscoelastic-plastic creep model of rock based on short time triaxial creep test[J]. Proceedings of Mining & Safety Engineering, 2011, 28(3): 446-451.
[16] 刘新喜, 童庆闯, 侯勇, 等. 高应力泥质粉砂岩非线性蠕变损伤模型研究[J]. 中国公路学报, 2018, 31(2): 280-288.
LIU Xinxi, TONG Qingchuang, HOU Yong, et al. Research on nonlinear creep damage model of high stress argillaceous siltstone[J]. Acta Sinica Sinica de Highway, 2018, 31(2): 280-288.
[17] 沈明荣, 谌洪菊. 红砂岩长期强度特性的实验研究[J]. 岩土力学, 2011, 32(11): 3301-3305.
SHEN Mingrong, CHEN Hongju. Testing study of long-term strength characteristics of red sandstone[J]. Rock and Soil Mechanics, 2011, 32 (11): 3301-3305.
[18] 崔旋, 佘成学. 推断岩石长期强度的黏塑性应变率法研究[J]. 岩石力学与工程学报, 2011, 30(S2): 3899-3904.
CUI Xuan, SHE Chengxue. Study of viscoplastic strain rate method to quickly determine long-term strength of rock. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S2): 3899-3904.
[19] 李良权, 徐卫亚, 王伟, 等. 基于流变实验的向家坝砂岩长期强度评价[J]. 工程力学, 2010, 27(11): 127-136, 143.
LI Liangquan, XU Weiya, WANG Wei, et al. Estimation of long term strength of Xiangjiaba sandstone based on rheological test[J]. Engineering Mechanics, 2010, 27(11): 127-136, 143.
[20] SZCZEPANIK Z, MILNE D, KOSTAKIS K, et al. Long term laboratory strength tests in hard rock[C]// ISRM 2003- Technology Roadmap for Rock Mechanics. Johannesburg: South African Institute of Mining and Metallurgy, 2003: 1179-1184.
[21] 范秋雁, 阳克青, 王渭明. 泥质软岩蠕变机制研究[J]. 岩石力学与工程学报, 2010, 29(8): 1555-1561.
FAN Qiuyan, YANG Keqing, WANG Weiming. Study on creep mechanism of muddy soft rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(8): 1555-1561.
[22] 赵延林,曹平,文有道,等. 岩石弹黏塑性流变实验和非线性流变模型研究[J]. 岩石力学与工程学报, 2008, 27(3): 477-486.
ZHAO Yanlin, CAO Ping, WEN Youdao, et al. Study on elasto-viscoplastic rheological test and nonlinear rheological model of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3): 477-486.
(编辑 陈灿华)
收稿日期:2018-08-30;修回日期:2018-10-22
基金项目(Foundation item):国家自然科学基金资助项目(51378082,51674041);长沙理工大学桥梁结构安全控制湖南省工程实验室基金资助项目(18KD04);湖南省研究生科研创新项目(CX2018B532) (Projects(51378082, 51674041) supported by the National Natural Science Foundation of China; Project(18KD04) supported by Open Fund of Engineering Laboratory of Bridge Structure Changsha University of Science & Technology of Hunan Province; Project(X2018B532) supported by Innovation Foundation of Postgraduate of Hunan Province)
通信作者:李盛南,博士研究生,从事岩土工程研究,E-mail:2561720910@qq.com