DOI: 10.11817/j.issn.1672-7207.2016.11.022

低渗致密气藏压裂水平井产能分析与完井优化

李波^{1, 2}，贾爱林¹，东博¹，甯波¹，王军磊¹

(1. 中国石油勘探开发研究院 鄂尔多斯分院，北京，100083；

2. 华能国际电力开发公司 燃气资源开发部，北京，100031)

摘要：基于压裂水平井产能影响因素较多，基于常规产能评价方法的单因素敏感性分析法不能对各因素的影响程度做出综合定量评价，在建立并求解考虑裂缝干扰、裂缝污染表皮系数、裂缝不同分布形式、裂缝与井筒有限导流的压裂水平井产能预测模型基础上，通过正交试验分析得到压裂水平井产能影响因素的主次顺序。研究结果表明：压裂水平井产能影响因素的主次顺序依次为地层渗透率、裂缝污染表皮系数、地层有效厚度、裂缝半长、裂缝条数、裂缝导流能力、水平段长度、井筒半径和裂缝分布形式，其中地层渗透率、裂缝污染表皮和有效厚度对产能的影响尤为显著，而井筒半径和裂缝分布形式对产能无明显影响。对于实际水平井，在储层渗透率、有效厚度和储层规模等因素均无法改变的条件下，应尽量降低作业对储层的伤害，并根据实际地质参数进一步优化裂缝参数，这对提高水平井产量和开发经济效益具有重要意义。

关键词：压裂水平井；裂缝；井筒；产能；正交试验；优化

中图分类号：TE37      文献标志码：A         文章编号：1672-7207(2016)11-3775-09

Productivity analysis and completion optimization of fractured horizontal wells in low-permeability tight gas reservoir

LI Bo^{1, 2}, JIA Ailin¹, HE Dongbo¹, NING Bo¹, WANG Junlei¹

(1. Ordos Basin Branch Institute, PetroChina Research Institute of Petroleum Exploration & Development,

Beijing 100083, China;

2. Gas Resources Development Department, Huaneng International Power Development Corporation,

Beijing 100031, China)

Abstract: Since there are many factors affecting the productivity of fractured horizontal wells, sensitivity analysis method based on conventional productivity evaluation method can not evaluate the impact of each factor comprehensively and quantitatively, a productivity prediction model was established considering interactive disturbance among fractures, skin factor of polluted fracture, fracture distribution form, finite flow in fracture and wellbore. A numerical iterative method to the model was also derived. Based on the prediction method, the sequence of the factors affecting the productivity of fractured horizontal wells was determined by orthogonal tests. The results show that the sequence of the factors affecting the productivity of fractured horizontal wells is as follows: formation permeability, pollution skin factor of fracture, net pay thickness, fracture half-length, number of fracture, fracture conductivity, effective length of horizontal wellbore, wellbore radius and fracture distribution form. It is worth pointing out that the effect of formation permeability, pollution skin of fracture and net pay thickness is significant, while the effect of wellbore radius and fracture distribution form is weaker. For a practical horizontal well, there remains precondition that formation permeability, reservoir permeability and reservoir scale are limited. Eliminating the formation damage due to stimulation and further optimizing fracture parameters based on geological data will be of great importance in improving productivity of individual well and increasing economic benefit.

Key words: fractured horizontal wells; fracture; wellbore; productivity; orthogonal test; optimization

压裂水平井作为提高气井产量和单井控制储量有效方式，在低渗致密气藏开发中得到广泛的应用^[1-3]。由于地层中形成多条压裂裂缝，压裂水平井流动由地层渗流、裂缝与井筒流动构成，准确评价其产能和分析其产能影响因素均有较大难度。关于压裂水平井产能评价方法，国内外有许多学者进行了研究^[4-10]，但这些预测模型均未全面考虑裂缝干扰、裂缝污染、裂缝非均匀分布、裂缝与井筒有限导流(存在流动压降)等客观物理现象，因此，不能客观地预测压裂水平井真实产能。关于压裂水平井产能影响因素的研究，目前普遍采用单因素敏感性分析法^[11-13]，少见对压裂水平井各因素的影响程度进行综合客观评价。为此，本文作者将通过位势理论和叠加原理，建立考虑裂缝干扰、裂缝污染表皮、裂缝非均匀分布、裂缝与井筒有限导流，以及包括裂缝-井筒汇聚流等客观物理现象的压裂水平井产能预测模型，并通过数值迭代法对模型进行求解；通过正交试验分析各因素对压裂水平井产能的影响程度、主次顺序，指出主控因素，再通过单因素敏感性分析法对完井参数进一步优化，为提高压裂水平井产量和开发经济效益提供指导。

1  压裂水平井产能评价方法

图1所示为压裂水平井示意图。为了优选压裂水平井参数，本文首先建立包含地层、裂缝和井筒耦合的流动数学模型(如图1所示)，并对模型进行以下假设：1) 微可压缩、均质等厚，顶底界面封闭地层；2) 气藏温度恒定，流体为可压缩干气，无特殊物理现象发生，不考虑重力作用的影响；3) 水平井水平段长度为L，压裂N条横向垂直裂缝，裂缝纵向上贯穿整个气层；4) 有限导流裂缝和井筒，即流体在裂缝和井筒内流动存在压降。

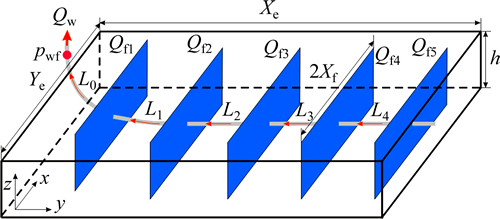
图1  压裂水平井示意图

Fig. 1  Sketch of fractured horizontal well

1.1  气层渗流模型

根据复势理论和叠加原理^[5-6]，水平井多段压裂情况下第i条裂缝的地层流入能力(产能)方程为

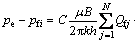
     (1)

式中：N为裂缝条数；R_e为供给半径，m；B为流体体积系数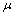；为流体黏度，mPa.s；h为储层有效厚度，m；k为气层渗透率，10^-3 μm²；X_fi为第i条裂缝半长，m；Q_fi为第i条裂缝产量，10⁴ m³/d；p_e为供给边界压力，MPa；p_fi为第i条裂缝压力，MPa；y_0i为第i条裂缝与x轴的距离，m；C为单位转换常数，1.157×10^-5。

对于在水平井压裂过程中，由压裂液与地层不配伍造成的裂缝表面污染的情况，则需要考虑流体沿裂缝表面流入裂缝产生的附加压力降，因此，其产能方程为

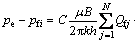
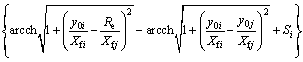       (2)

对于气井，根据真实气体状态方程，可得到裂缝地面标准条件下的产能方程为

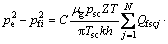
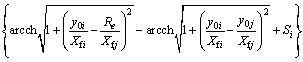   (3)

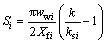              (4)

式中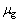：为天然气黏度，mPa.s；Z为天然气压缩因子；p_sc为地面标准条件下压力，MPa；T_sc为地面标准条件下压力，K；Q_fsci为地面标准条件下第i条裂缝产量，10⁴ m³/d；T为气藏热力学温度，K；k_si为裂缝污染带渗透率，10^-3 μm²；w_si为污染带宽度，m；S_i为裂缝污染表皮系数。

1.2  裂缝流动模型

对低渗致密油气藏，一般压裂导流能力相对较低的长裂缝，裂缝内流动存在压降。本文在假设裂缝为均匀流入裂缝，裂缝内的流动包括远井筒处的水平线性流和近井筒带的径向汇聚流情况下，得到有限导流裂缝内流动方程为

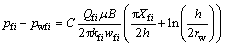       (5)

对于气井，则根据真实气体状态方程将裂缝地下产量转化为地面标准条件下的产量方程，得到裂缝内流动压降表达式为

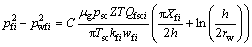   (6)

式中：k_fi为裂缝渗透率，10^-3 μm²；w_fi为裂缝宽度，m；r_w为水平井筒半径，m；Q_fsci为地面标准条件下第i条裂缝产量，10⁴ m³/d；p _wfi为第i条裂缝处井筒压力，MPa。

1.3  井筒流动模型

取压裂水平井井筒流动段元(见图2所示)，根据流体力学基本定理，可得到水平井井筒压力梯度方程为

     (7)

式中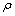：为流体密度，kg/m³；L为井筒段长度，m；D为井筒直径，m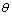；为井筒倾斜角，(°)；g为重力加速度，m/s²；v为流动速度，m/s；p为压力，MPa；f为摩擦阻力系数。

式(7)中第1项为重力压降，第2项为摩阻压降，第3项为加速度压降。对于水平井水平段，垂向位移较小，重力压降可以忽略不计。

对于气井，根据真实气体状态方程，压裂水平井井筒摩擦压降梯度为

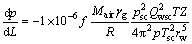         (8)

对式(8)在第(i-1)条裂缝右端到第i条裂缝左端之间的井筒段进行积分，可得

(i=1, 2, …, N)               (9)

通过式(9)可以计算出第(i-1)条裂缝右端到第i条裂缝左端之间的摩阻压降。

由于不考虑地层流体直接流入井筒，因此，第(i-1)条裂缝右端到第i条裂缝左端之间加速压降为零。对于有压裂裂缝的井筒处，会由于裂缝中流体的径向汇聚流入引起加速度压降，如图2中的第i条裂缝，其左右两端的加速度压降可表示为

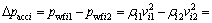
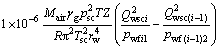     (10)

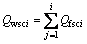 (i=1, 2, …, N)         (11)

取第i条裂缝左右两端处压力的平均值为第i条井筒裂缝处压力，即

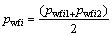             (12)

式中：M_air为空气摩尔质量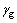；为天然气相对密度；R为摩尔气体常数；Q_wsci为第i井筒段内地面条件下的流量，m³/s；Q_fsci为第i条裂缝地面条件下的产量，10⁴ m³/d；v_i1和v_i2分别为第i条裂缝右端、左端处的流体流速，m/s；p_wfi1和p_wfi2分别为第i条裂缝右端、左端处的流体压力，MPa。

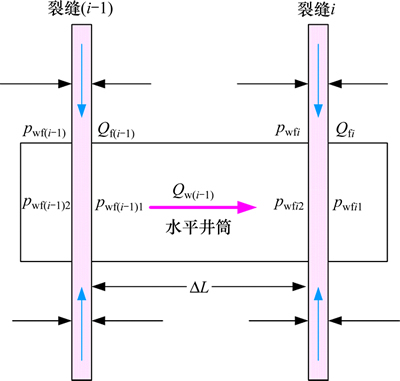
图2  水平井井筒流动示意图

Fig. 2  Flow pattern in the horizontal wellbore

1.4  模型求解与验证

由计算井筒摩阻压降的式(9)与加速度压降的式(10)、式(3)与式(6)联立可组成3N个线性方程组，其中共有3N个未知变量，分别为Q_fsci，p_wfi1和p_wfi2 (i=1, 2, …, N)，方程个数与未知量个数相等，因此，可以进行封闭求解。由于方程组中的变量间具有复杂的线性关系，采用迭代法进行求解，具体算法是先假定裂缝和井筒不存在压降，通过计算裂缝初始产量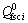，然后从第1条压裂裂缝起根据式(9)~(11)依次计算各条裂缝两端的压力p_wfi1和p_wfi2，利用式(12)计算裂缝处井筒压力p_wfi，然后将p_wfi代入式(3)和式(6)计算有限导流裂缝和井筒下裂缝产量Q_fsci。如此反复循环计算，直到满足收敛条件为止。最后计算压裂水平井总产量Q_sc：

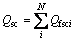              (13)

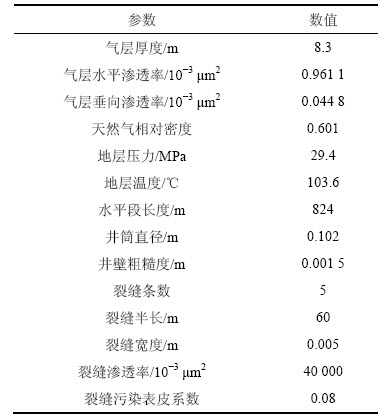
X1井为某致密砂岩气田一口压裂水平井，完钻井深4 319 m，水平段长度为824 m，采用裸眼封隔器分段压裂5段完井，从水平井筒的趾端到根端，压裂裂缝间距不等，依次为115，100，120和160 m。投产后对X1井进行了修正，气层基本参数与压力恢复曲线分析结果如表1所示，修正等时试井结果表明X1井无阻流量为55.04×10⁴ m³/d。

表1  X1井基本参数

Table 1  Basic data of well X1

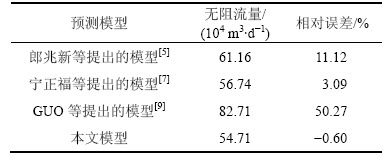
根据X1井的基本参数(表1)，分别利用郎兆新等^{[5, 7, 9]}提出的模型和本文模型计算X1井的无阻流量，结果如表2中所示。由表2可知：GUO等^[9]提出模型计算结果较测试结果明显偏大，相对误差达50.27%；其次为郎兆新模型^[5]，相对误差为11.12%；而本文模型的误差最小，为-0.60%，宁正福模型^[5]的相对误差介于郎兆新模型与本文模型之间。Guo模型计算结果误差较大的一方面原因是假设流体从地层到裂缝和裂缝内的流动均为线性渗流，这与压裂水平井稳态或拟稳态流动状态下为椭圆流动的实际有一定的差异；另一方面是Guo模型没有考虑裂缝间相互干扰造成裂缝产量的差异性，以及井筒中存在压降的客观事实。此外，对比各种模型的计算结果可知：在X1井气层和完井参数组合条件下，考虑裂缝干扰和裂缝·井筒聚流效应的宁正福模型具有较高的预测精度，相对误差小于5%，但同时考虑裂缝干扰、裂缝污染表皮系数、裂缝与井筒有限导流、裂缝内高速非达西流动的本文模型计算精度更高。

表2  不同水平井产能预测模型预测结果对比

Table 2  Predicting results comparison between different models

2  正交试验法分析压裂水平井产能影响因素

2.1  正交试验设计基本原理

在多因素、多水平试验中，如果对每个因素的每个水平都互相搭配进行全面试验，需要进行的试验次数就会很多。由田口玄一提出的正交试验方法是在多因素优化试验中利用数理统计学与正交性原理，从大量的试验点中挑选有代表性和典型性的试验点，应用“正交表”科学合理地安排试验，从而用尽量少的试验得到最优试验结果的一种方法^[14-16]。

正交试验具有2条重要性质，即水平的均匀性和搭配的均匀性。水平的均匀性是指在所有试验方案中，每个因素及因素的水平值都是均匀分配的；搭配的均匀性是指每个因素的每个水平值在所有试验方案中出现的次数均等，而且任意2个因素组合出现的次数也相等。正交试验是通过正交表(确定试验点)来安排试验，正交表的符号表示为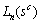。式中：L为正交表的代号；n为正交表的横行数，即试验方案数；c为正交表的列数，表示因素的个数；s为因素的水平数。

正交试验结果的分析方法有直观分析法(极差分析法)和方差分析法。直观分析法具有简单方便、易于掌握的特点，就是将各参数每个水平值对试验指标影响的大小，通过直观分析图或极差来表示，然后综合对比分析确定最优试验参数组合。方差分析法是利用数理统计法将数据的总偏差分解成因素引起的偏差和误差引起的偏差2部分，构造F统计量，进行F检验，从而判断各参数对试验指标影响的显著程度和可信程度。

2.2  正交试验设计

利用前文所建立的压裂水平井产能评价方法，分析不同因素对产能的影响，具体包括：气层渗透率(A)、有效厚度(B)、井筒半径(C)、水井段长度(D)、裂缝条数系数(E)、裂缝半长(F)、裂缝导流能力(G)、裂缝污染表皮系数(H)和裂缝分布形式(I)。

苏里格气田为典型低孔、低渗、低丰度气藏，储层孔隙度为5%~12%，平均孔隙度为8.9%，常压空气渗透率为0.1×10^-3~1.0×10^-3 μm²，平均渗透率为0.54×10^-3 μm²，含气饱和度为55%~65%，平均有效储层厚度为10.2 m。根据苏里格气田150口压裂水平井实钻资料统计结果，设计各因素的水平如表3所示，并通过正交试验表L₃₂(4⁹)完成试验设计，各因素组合及试验结果如表4所示(压裂水平井的生产压差均为5.0 MPa)。

2.3  试验结果分析

1) 极差分析。利用前文介绍的方差分析法对试验结果进行分析，结果如表5所示。由表5中极差可知影响压裂水平井产能因素的主次顺序为：A，H，B，F，G，E，C，I，C，即地层渗透率影响最大，污染表皮系数次之，再其次为地层有效厚度、裂缝半长、裂缝条数、裂缝导流能力、水平段长度，而井筒半径和裂缝分布形式对产量影响不明显。

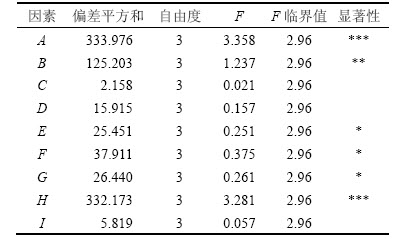
2) 方差分析。根据方差分析法正交试验结果进行分析，结果如表6所示。由表6可知：地层渗透率(A)和裂缝污染表皮系数(H)对产能的影响最为显著，其次是地层有效厚度(B)的影响较为显著，裂缝半长(F)、裂缝条数(E)、裂缝导流能力(G)和水平段长度(D)对产量有影响，但相对不明显，而井筒半径和裂缝分布形式对产能影响不显著。方差分析结果与极差分析结果一致。

表3  试验因素及其水平值

Table 3  Testing factors and levels

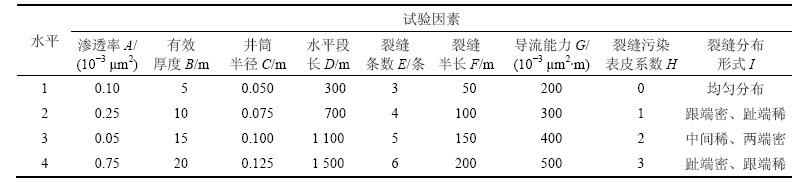
表4  正交试验设计表(9因素4水平)

Table 4  Orthogonal tale of 9 factors and 4 levels

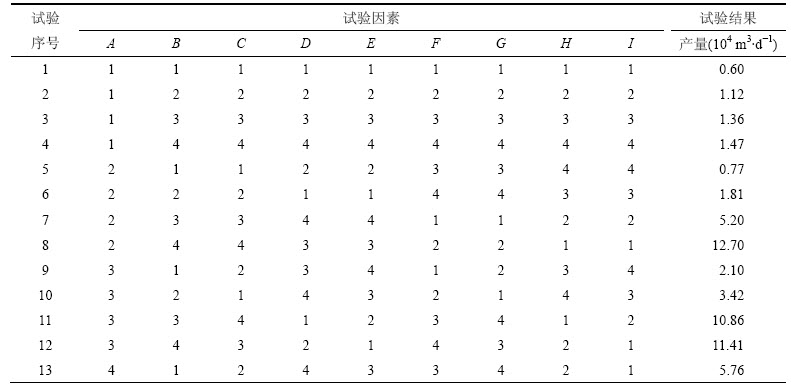
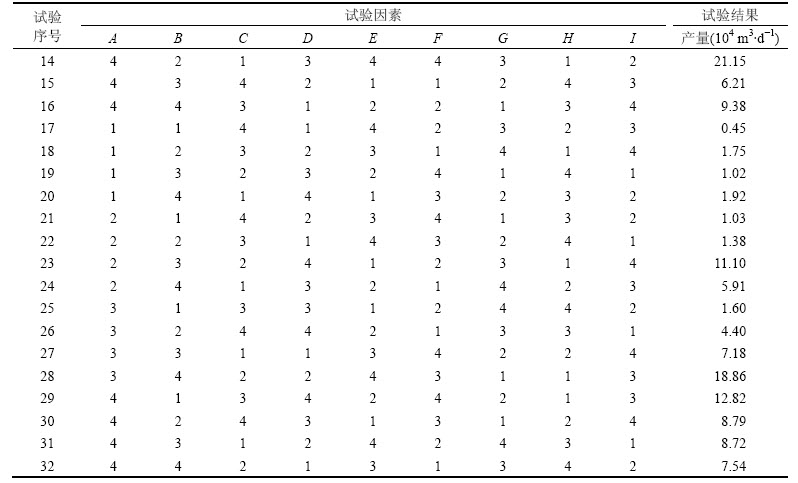
表5  极差分析结果

Table 5  Results of range analysis

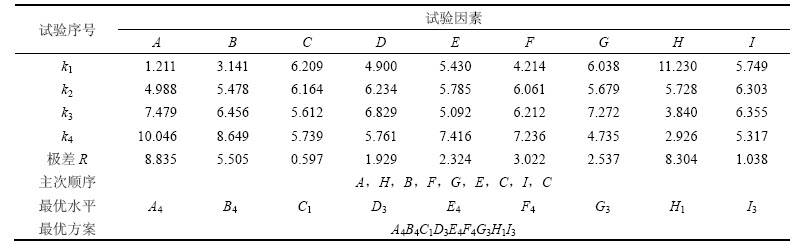
表6  方差分析结果表

Table 6  Results of variance analysis

通过上述研究可知各因素对致密气藏压裂水平井产能大小的影响顺序依次为地层渗透率、裂缝污染表皮系数、地层有效厚度、裂缝半长、裂缝条数、裂缝导流能力、水平段长度、井筒半径和裂缝分布形式，其中地层渗透率、裂缝污染表皮系数和地层有效厚度对产能的影响尤为显著。

3  实际井完井优化

在实际油气田开发过程中，压裂水平井的部署一方面需考虑地层渗透率、有限厚度和储层规模(限制水平段钻进长度)等客观地质因素，另一方面需考虑投资成本的问题，特别是对压裂改造成本的考虑。苏里格气田压裂水平井平均单井总投资约3 100万元，其中钻井成本约2 000万元，压裂改造成本约1 100万元，压裂改造占水平井总投资成本的1/3。因此，在实际油气田水平井开发过程中，根据实际地质参数进一步优化裂缝参数对提高水平井产量和开发经济效益具有重要意义。

X2井为苏里格气田一口压裂水平井，钻遇气层原始地层压力为29.01 MPa，孔隙度为8.81%，渗透率为0.55×10^-3 μm²，有效厚度为14.5 m，完钻井深为4 514 m，水平段长度为1 104 m，井筒半径为0.05 m。根据压裂水平井产能影响因素分析结果，结合X2井的实钻地质资料，开展裂缝参数和井筒半径优化研究，结果如图3和图4所示。

由图3可知：压裂水平井产气指数随裂缝条数、裂缝半长、裂缝导流能力的增大而增大，随裂缝污染表皮系数的增加而急剧下降；裂缝条数、裂缝半长、裂缝导流能力存在最优值；当参数取值大于最优值时，压裂水平井的产气指数随参数增大而增大的趋势明显变缓。为了在有效投资成本范围内使水平井获得较高产能，确定X2井裂缝参数的最优值如下：裂缝条数为5条，裂缝半长为60 m、裂缝导流能力为40×10^-3 μm²·m，裂缝污染表皮系数0。根据参数优化结果，利用本文模型预测X2井产气指数为2.898×10⁴  m³/ (d·MPa)，X2井实际压裂投产后初期产量为 17.86×10⁴ m³/d，生产稳定后产量为21.34×10⁴ m³/d，井口压力为17.62 MPa，折算井底流压为21.45 MPa，产气指数为2.827×10⁴ m³/(d·MPa)，与预测产气指数的相对误差为2.53%，说明本文产能预测模型具有较高的预测精度，满足工程计算精度要求。

由图4可知：水平井井筒半径对井筒压降有影响，当井筒半径小于0.044 3 m时，水平井井筒压降随半径的增大而减小，但当井筒半径大于0.044 3 m后，井筒半径对井筒压降影响不明显。因此，X2井水平优化井筒段半径为0.044 3 m。

根据上述完井参数优化结果，利用本文模型计算X2井各条裂缝产量和井筒压力分布，结果如图5所示。由图5可知：压裂水平井各条裂缝的产量不等，并且差异较大，水平段两端裂缝产量高，中间裂缝产量低，这是由于压裂水平井裂缝干扰造成的结果，水平两端裂缝的泄流面积相对较大，产量也相对较高。压裂水平井井筒内存在压降，从水平井的趾端到跟端，裂缝处井筒压力逐渐降低，特别是在靠近水平井跟端的井筒部位，压降较大，因为越靠近跟端，水平井筒的流量越大，压降也越大。由于水平井筒内流动存在压降，水平井筒对称位置上的裂缝(如裂缝1与裂缝5、裂缝2与裂缝4)产量略有差异，靠近水平井筒跟端的裂缝产能略高于靠近趾端的对称裂缝产能，如裂缝1的产量为5.33×10⁴ m³/d，而裂缝5的产量为5.30×10⁴ m³/d。

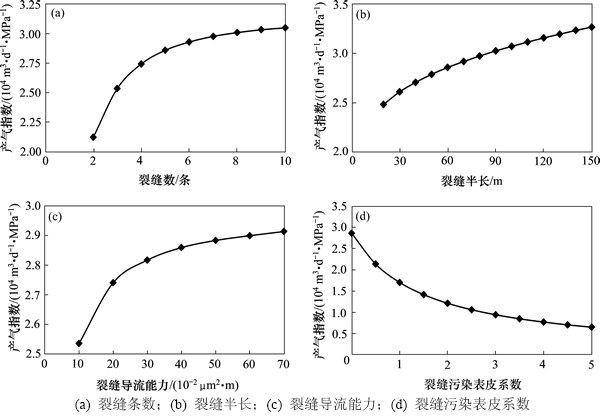
图3  裂缝参数对压裂水平井产能的影响

Fig. 3  Effect of fracture parameters on productivity of fractured horizontal well

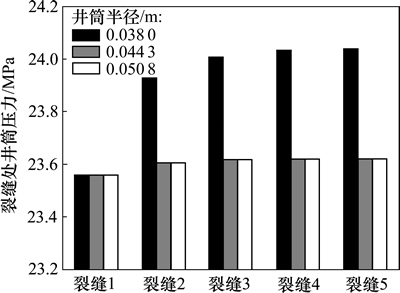
图4 不同井筒半径下水平井井筒压力分布

Fig. 4  Pressure profile in horizontal wellbore under different wellbore radius

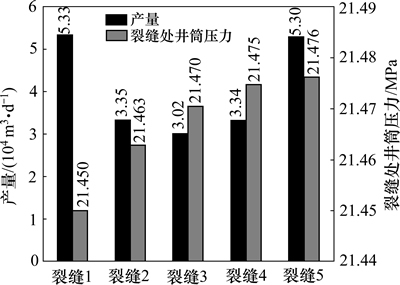
图5  优化参数组合下裂缝产量与井底流压分布

Fig. 5  Gas rate and wellbore pressure of different fractures under optimal design

4  结论

1) 应用位势理论、叠加原理和流体力学的相关原理，建立了考虑裂缝干扰、裂缝污染表皮系数、裂缝非均匀分布、裂缝与井筒有限导流的压裂水平井产能预测模型，并给出了模型的数值求解方法。

2) 通过正交试验分析得出了压裂水平井产能影响因素的主次顺序为地层渗透率、裂缝污染表皮系数、地层有效厚度、裂缝半长、裂缝条数、裂缝导流能力、水平段长度、井筒半径和裂缝分布形式，其中地层渗透率、裂缝污染表皮系数和地层有效厚度对产能的影响尤为显著，而井筒半径和裂缝分布形式对产能影响不明显。

3) 正交试验分析结果从理论上给出了压裂水平井获得高产的重要前提条件，这对于压裂水平井部署和完井优化具有重要指导意义；对于油气田开发中实际水平井，在储层渗透率、厚度和储层规模等因素均无法改变条件下，应尽可能降低作业(钻井和压裂)对储层的伤害，并根据实际地质参数进一步优化裂缝参数，这对提高水平井产量和开发经济效益具有重要意义。

参考文献：

[1] 马新华, 贾爱林, 谭健, 等. 中国致密砂岩气开发工程技术与实践[J]. 石油勘探与开发, 2012, 39(5): 572-579.

MA Xinhua, JIA Ailin, TAN Jian. Tight sand gas development technologies and practices in China[J]. Petroleum Exploration and Development, 2012, 39(5): 572-579.

[2] 何东博, 贾爱林, 冀光, 等. 苏里格大型致密砂岩气田开发井型井网技术[J]. 石油勘探与开发, 2013, 40(1): 79-89.

HE Dongbo, JIA Ailin, JI Guang. Well type and pattern optimization technology for large scale tight sand gas, Sulige gas field[J]. Petroleum Exploration and Development, 2013, 40(1): 79-89.

[3] 卢涛, 张吉, 李跃刚, 等. 苏里格气田致密砂岩气藏水平井开发技术及展望[J]. 天然气工业, 2013, 33(8): 38-43.

LU Tao, ZHANG Ji, LI Yuegang, et al. Horizontal well development technology for tight sand stone gas reservoirs in the Sulige Gas Field, Ordos Basin[J]. Nature Gas Industry, 2013, 33(8): 38-43.

[4] JOSHI S D. Augmentation of well productivity using slant and horizontal wells[J]. JPT, 1988, 40(6): 729-739.

[5] 郎兆新, 张丽华, 程林松. 压裂水平井产能研究[J].石油大学学报, 1994, 18(2): 43-46.

LANG Zhaoxing, ZHANG Lihua, CHENG Linsong. Investigation on productivity of fractured horizontal well[J]. Journal of the University of Petroleum, China, 1994, 18(2): 43-46.

[6] 韩树刚, 程林松, 宁正福. 气藏压裂水平井产能预测新方法[J]. 石油大学学报(自然科学版), 2002, 26(4): 36-39.

HAN Shugang, CHENG Linsong, NING Zhengfu. A new method for predicting productivity of fractured horizontal wells in gas reservoir[J]. Journal of the University of Petroleum, China, 2002, 26(4): 36-39.

[7] 宁正福, 韩树刚, 程林松, 等. 低渗透油气藏压裂水平井产能计算方法[J]. 石油学报, 2002, 23(2): 68-72.

NING Zhengfu, HAN Shugang, CHENG Linsong, et al. Productivity calculation method of fractured horizontal wells in low permeability oil or gas field[J]. Acta Petroleum Sinica, 2002, 23(2): 68-72.

[8] 范子菲, 方宏长, 牛新年. 裂缝性油藏水平井稳态解产能公式研究[J]. 石油勘探与开发, 1996, 23(3): 52-57.

FAN Zifei, FANG Hongchang, NIU Xinnian. A steady solution formula of horizontal well productivity in a fractured reservoir[J]. Petroleum Exploration and Development, 1996, 23(3): 52-57.

[9] GUO B, YU X, KHOSHGAHDAM M. A simple analytical model for predicting productivity of multi-fractured horizontal wells[J]. SPE Reservoir Evaluation & Engineering, 2009, 12(6): 879-885.

[10] 王志平, 朱维耀, 岳明, 等. 低、特低渗透油藏压裂水平井产能计算方法[J]. 北京科技大学学报, 2012, 34(7): 750-754.

WANG Zhiping, ZHU Weiyao, YUE Ming, et al. A method to predict the production of fractured horizontal wells in low/ultra-low permeability reservoirs[J]. Journal of University of Science and Technology Beijing, 2012, 34(7): 750-754.

[11] 张学文, 方宏长, 裘怿楠, 等. 低渗透率油藏压裂水平井产能影响因素[J]. 石油学报, 1999, 20(4): 51-56.

ZHANG Xuewen, FANG Hongchang, QIU Yinan, et al. A study on factors affecting the performance of hydraulically fractured horizontal well in low permeability reservoirs[J]. Acta Petroleum Sinica, 1999, 20(4): 51-56.

[12] 曾凡辉, 郭建春, 徐严波, 等. 压裂水平井产能影响因素[J]. 石油勘探与开发, 2007, 34(4): 474-478.

ZENG Fanhui, GUO Jianchun, XU Yanbo, et al. Factors affecting production capacity of fractured horizontal wells[J]. Petroleum Exploration and Development, 2007, 34(4): 474-478.

[13] 王军磊, 贾爱林, 何东博, 等. 致密气藏分段压裂水平井产量递减规律及影响因素[J]. 天然气地球科学, 2014, 25(2): 278-285.

WANG Junlei, JIA Ailin, HE Dongbo, et al. Rate decline of multiple fractured horizontal well and influence factors on productivity in tight gas reservoirs[J]. Natural Gas Geoscience, 2014, 25(2): 278-285.

[14] 刘应红, 李宗田, 赵碧华. 利用正交试验设计方法优选低渗油藏整体压裂方案[J]. 断块油气田, 2000, 7(3): 46-50.

LIU Yinghong, LI Zongtian, ZHAO Bihua. Optimization of fracturing project for low permeable reservoir with orthogonal and analysis experiments[J]. Fault-Block Oil & Gas Field, 2000, 7(3): 46-50.

[15] 韩兴刚, 徐文, 刘海锋. “正交试验法”在油气田开发方案优化设计中的应用[J]. 天然气工业2005, 25(4): 116-118.

HAN Xingang, XU Wen, LIU Haifeng. Application of “cross experimental method” in optimized design of development program for oil/gas fields[J]. Nature Gas Industry, 2005, 25(4): 116-118

[16] 董家辛, 童敏, 张金, 等. 基于正交试验方法的气藏水平井参数优选[J]. 天然气地球科学, 2012, 23(3): 584-589.

DONG Jiaxin, TONG Min, ZHANG Jin, et al. Optimization of horizontal well parameter based on orthogonal test method[J]. Natural Gas Geoscience, 2012, 23(3): 584-589.

(编辑  陈爱华)

收稿日期：2016-01-20；修回日期：2016-03-25

基金项目(Foundation item)：国家科技重大专项(2011ZX05015) (Project(2011ZX05015) supported by the National Science and Technology Major Project

通信作者：李波，博士，工程师，从事气藏工程方面的研究；E-mail: libosonova@163.com