Simulation of bulk metal forming processes using one-step finite element approach based on deformation theory of plasticity
来源期刊:中国有色金属学报(英文版)2010年第2期
论文作者:WANG Peng 董湘怀 傅立军
文章页码:276 - 282
Key words:bulk metal forming; plastic deformation theory; finite element method; one-step forward simulation; rigid-plastic materials
Abstract: The bulk metal forming processes were simulated by using a one-step finite element (FE) approach based on deformation theory of plasticity, which enables rapid prediction of final workpiece configurations and stress/strain distributions. This approach was implemented to minimize the approximated plastic potential energy derived from the total plastic work and the equivalent external work in static equilibrium, for incompressibly rigid-plastic materials, by FE calculation based on the extremum work principle. The one-step forward simulations of compression and rolling processes were presented as examples, and the results were compared with those obtained by classical incremental FE simulation to verify the feasibility and validity of the proposed method.
基金信息:the National Natural Science Foundation of China
the Specialized Research Fund for the Doctoral Program of Higher Education of China

WANG Peng(王 鹏), DONG Xiang-huai(董湘怀), FU Li-jun(傅立军)
Department of Plasticity Technology, Shanghai Jiao Tong University, Shanghai 200030, China
Received 7 November 2008; accepted 14 January 2009
Abstract: The bulk metal forming processes were simulated by using a one-step finite element (FE) approach based on deformation theory of plasticity, which enables rapid prediction of final workpiece configurations and stress/strain distributions. This approach was implemented to minimize the approximated plastic potential energy derived from the total plastic work and the equivalent external work in static equilibrium, for incompressibly rigid-plastic materials, by FE calculation based on the extremum work principle. The one-step forward simulations of compression and rolling processes were presented as examples, and the results were compared with those obtained by classical incremental FE simulation to verify the feasibility and validity of the proposed method.
Key words: bulk metal forming; plastic deformation theory; finite element method; one-step forward simulation; rigid-plastic materials
1 Introduction
In 1970s, LEVY et al[1] applied plastic deformation theory to the finite element(FE) simulation of sheet metal forming processes and developed one-step inverse approach. In this method, the final part shapes are prescribed and the initial blank sheet configurations are solved, satisfying the external force conditions based on the finite element formulation taking account of deformation theory as well as static equilibrium condition. The one-step calculation is capable of efficiently handling complicated sheet forming problems and providing that the results are in close agreement with incremental FE predictions.
Bulk metal forming processes are nonlinear and large deformation problems, which are solved by incremental FE simulation in general[2-3]. Compared with sheet forming processes, the deformation path and the contact history between workpiece and tool in bulk forming processes are more complicated. It is much difficult to apply the deformation theory to bulk forming simulation[4-5]. Consequently, despite the remarkable progresses that have been achieved in one-step approach for sheet metal forming simulation[6-8], the applications in bulk metal forming are seldom studied.
In recent years, only a limited number of researchers devoted to the solution of bulk metal forming processes by means of deformation theory. The ideal flow theory based on deformation theory has been already applied for plane strain and axisymmetric bulk forming problems[9-11]. This approach involves strict assumption for the minimum plastic work path, so that it may not be feasible for conventional forming processes and tools. A large time increment (LATIN) method was put forward for non-linear mechanical behaviour, adopting an iterative procedure that takes the whole loading process into account in one step by internal variables[12]. This method has already been applied to the metal forming processes simulation[13-15]. But, it is difficult to understand the principle and implementation procedure of the algorithm. SIMO and ORTIZ[16] and BRUNIG[17] built a framework of nonlinear FE procedure for finite deformation elastoplastic problems based on deformation theory of plasticity. In this method, a hyperelastic constitutive law based on a free energy potential function was used, in which stress measurements were related to Green strain. This procedure has been applied to bulk forming permitting large increment size. However, it has not been investigated to solve practical problems involving contact condition by this method.
In the present work, the bulk metal forming problems were analyzed by a one-step FE approach based on deformation theory of plasticity[18-19].
2 One-step FE simulation scheme
One-step FE approach for bulk metal forming has some different features from the incremental FE approach. It is based on the plastic potential energy, relating the initial configuration to the final configuration in one step. The solution was obtained by minimization of the function, which is an approximated plastic potential energy derived from the total plastic work and the equivalent external work.
2.1 Kinematics
Due to the large computing step size between the initial and the final configurations, it is inevitable to consider the geometrical non-linearity. In the Cartesian coordinate system, by adopting Lagrangian description, Green strain tensor related to the displacement is defined as
![]() (1)
(1)
The strain field can be defined over the elements by the nodal displacement vector as
{ε}![]() (2)
(2)
where {ε} is the strain vector, ![]() for axisymmetric problem,
for axisymmetric problem, ![]() for plain problem; and the geometric matrix [B] is decomposed as
for plain problem; and the geometric matrix [B] is decomposed as
![]() (3)
(3)
where [BL] and [BN] are linear and nonlinear items of geometric matrix, respectively, which are given explicitly as follows:
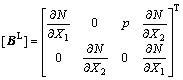 (4)
(4)
![]() (5)
(5)
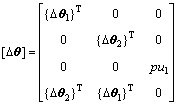 (6)
(6)
![]() (7)
(7)
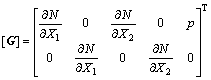 (8)
(8)
where p=N/X1 for axisymmetric problem; and p=0 for plain problem.
2.2 Constitutive equation
Constitutive equation for one-step FE approach is based on Ilyushin deformation theory, which is suitable for the work hardening material, ignoring elasticity. Adopting Mises yield condition, the constitutive relationship between stress and total strain is defined as
![]() (9)
(9)
where ![]()
![]() σ′ij and
σ′ij and ![]() are the equivalent stress, the equivalent strain, the components of stress deviator and plastic strain, respectively. The strain is a function of current stress state, independent of stress history.
are the equivalent stress, the equivalent strain, the components of stress deviator and plastic strain, respectively. The strain is a function of current stress state, independent of stress history.
The equivalent strain is defined by
![]() (10)
(10)
Through estimation of total strain {ε}, we can compute ![]() by Eq.(10), then estimate the stress by Eq.(9). This operation is performed for each numerical integration point by iterations.
by Eq.(10), then estimate the stress by Eq.(9). This operation is performed for each numerical integration point by iterations.
2.3 Plastic deformation energy
Based on the constraint variational principle and deformation theory, by taking the deforming body and specified surface tractions as a system, energy function is expressed in current configuration in static equilibrium by the principle of extremum work. The incompressibility is enforced by penalty function. Then, we can establish the functional as
![]()
(11)
where α is the penalty factor; εV is the volumetric strain; f is the surface traction; and u is the displacement of the traction surface.
Among admissible displacement fields satisfying the condition of compatibility and incompressibility, as well as the displacement boundary conditions, the actual solution minimizes the function. After finite-element discretization, a nonlinear equation system is established by minimizing ![]() :
:
![]()
![]() (12)
(12)
where
![]() (13)
(13)
The geometrical nonlinear items containing BN are transposed as fictitious load directly, and geometrical nonlinearity is omitted in penalty function item.
Eq.(12) is solved iteratively by using the Newton-Raphson method
![]() (14)
(14)
where
![]()
![]()
![]() (15)
(15)
where b=(BL)TBLue; [Kf] is the item by frictional work. Eq.(14) can be written in following form
![]() (16)
(16)
where K is the stiffness matrix and P is the residual of the nodal point force vector.
2.4 Boundary conditions
Since the large time step is involved, the contact boundary conditions between the workpiece and the tool are simply treated. A fictitious sliding constraint surface is introduced to replace the geometry of tool and to guide the movement of boundary nodes only on it during Newton-Raphson iterations, dispensing with treatment of contact. Moreover, it is inevitable to estimate the work of the external force through considering the history of contact by means of equivalent method. As for some bulk forming processes, the equivalent work of external force can be estimated by recording the relative tangential displacements of boundary nodes on the sliding constraint surface between the initial and final configurations. The shear friction model is adopted. Because this model is velocity-dependent, the displacement is converted into pseudo-velocity by introducing the virtual loading time. The friction force model is expressed by
![]() (17)
(17)
where f is the friction coefficient; k is the shear strength, ![]() ; u0 is a constant, u0=10-5; and Δus is the relative node velocity, which is the pseudo velocity by means of dividing displacement by virtual loading time.
; u0 is a constant, u0=10-5; and Δus is the relative node velocity, which is the pseudo velocity by means of dividing displacement by virtual loading time.
The fictional work item in the function is
![]() (18)
(18)
The local coordinates are employed to define the sliding constraint surface for each boundary nodal point. The stiffness matrix K and the residual force vector P should be transformed into the local coordinates using the transformation matrix T
![]() (19)
(19)
where
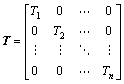 (20)
(20)
![]() (21)
(21)
where the subscript i designates the node number; and θi is the angle from the global coordinate to the local coordinate in counterclockwise direction.
2.5 Initial guess of displacement field
Because of large step length between adjacent configurations, the deformed history is considered approximately, which results in high nonlinearity in the computation. It is prerequisite to get a reasonable initial solution of displacement to start calculation. Compared with sheet forming, the shapes of billet and workpiece in bulk forming are more complicated. As far as forward simulation of bulk forming using deformation theory, it is necessary to preset the final configuration according to incompressible condition, forming processing and tools etc, before getting the initial solution. Then, we can obtain two sets of FE meshes with the same topological relationship on the initial and the finial configurations by means of mapping.
For example, in compression of square rod, the final workpiece configuration could quite easily be preset by satisfying the volume constancy and guessing the barrel profile. Then, meshes are generated by mapping. The procedure of mesh mapping is described as follows. Firstly, the initial meshes of billet are projected to the workpiece along the height direction, namely, the boundary nodes on the top and bottom surfaces of the billet are projected on the top and bottom surfaces of the workpiece respectively. Then, all inside nodes are distributed uniformly along the height direction, without changing width coordinates of all nodes. At last, the width projection of meshes is performed by the same method.
3 Numerical examples
Based on the above formulations, the one-step simulation program for bulk metal forming using deformation theory of plasticity is developed. For comparison, ABAQUS/Standard is used to provide simulation results of incremental FE approach.
3.1 Compression of square rod
The compression of square rod is studied as an example due to its relevance in bulk metal forming application. Width and height of billet are 20 mm and 15 mm, respectively. Material hardening behaviour is assumed to be ![]() f=0.1. The one-step forward simulation is performed under plain strain assumptions, and symmetry FE models are accomplished by discretizing only half the cross section of the geometry by means of 150 four-node quadrilateral elements and 176 nodes.
f=0.1. The one-step forward simulation is performed under plain strain assumptions, and symmetry FE models are accomplished by discretizing only half the cross section of the geometry by means of 150 four-node quadrilateral elements and 176 nodes.
From Fig.1, it can be seen that similar barrel profiles are obtained by both one-step and incremental simulations. By taking the contact histories of workpiece and tool into account equivalently, the effect of frictional work on deformation is realized. It seems to indicate that the one-step FE approach has a tendency to underestimate the barreling effect. These discrepancies maybe mainly result from the employment of simplified method to deal with frictional work.
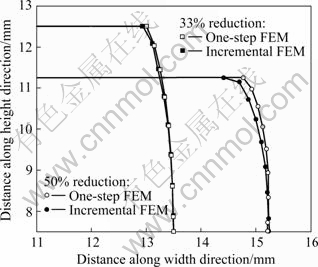
Fig.1 Comparison of barrel profiles obtained by one-step and incremental FE simulation
Fig.2 presents the comparison of equivalent stress from the center to the outside of the billet along the width and height directions by one-step and incremental FE simulations. The average errors along the width and height directions are 0.57% and 2.21%, respectively. These discrepancies maybe mainly derive from the employment of deformation theory, large step kinematic description and simple method to deal with boundary condition. However, the result of one-step FE approach is still acceptable.
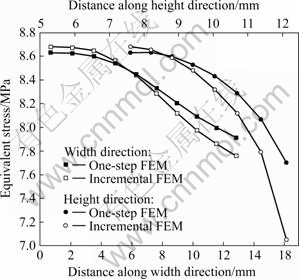
Fig.2 Comparison of equivalent stress distributions obtained by one-step and incremental FE simulations at height reduction of 33%
Fig.3 presents the comparison of equivalent plastic strain contours by one-step and incremental FE simulations. It can be seen that the strain distributions by both methods are in good agreement on the whole.
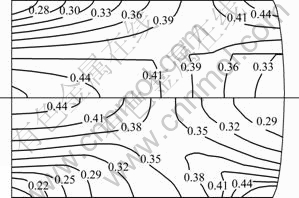
Fig.3 Comparison of equivalent plastic strain contours by one-step (upper) and incremental (lower) FE simulations at height reduction of 33%
The computing step number and the computing time at height reduction of 33% by the two methods are compared in Table 1. All the one-step computations adopt one increment step, and the iteration number is less. The calculation is executed on a personal computer with Pentium(R) 4 CPU 3.0 GHz and 1 GB memory. Apparently, one-step FEM is more efficient than incremental FEM. The average time saving is up to about 72%.
Table 1 Comparison of computing step number and computing time between one-step and incremental FE approaches

One-step FE approach deals with the total amount of deformation between two configurations by the principle of extremum work, whereas the effect of deformation history is only implicit. The calculated results of one-step simulation for compression are quite accurate, which may be attributed to the approximation of linear strain path in the process. From Fig.4, we can see that the ratio of the principal true strain for compression of square rod is almost constant during deformation.
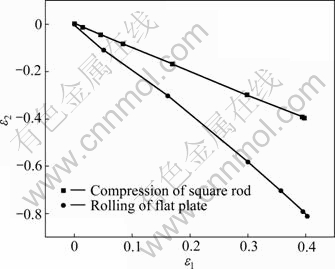
Fig.4 Deformation paths of compression of square rod and rolling of flat plate
3.2 Rolling of flat plate
Rolling of flat plate is a basic metal manufacturing technique, in which the deformation path is almost linear (Fig.4) and friction plays an important role as it is the only mechanism by which the plate is pulled through the roll stand. Thus, it encounters both opportunity and challenge to perform one-step calculation.
There are discontinuous effects of friction on deformation during the plate rolling. The contact situation of metal in the deformation zone is shown in Fig.5. Initially, the plate is drawn by the roller. When the plate contacts with the roller, the plate moves slower than the roller surface. The plate presents a relative slip in the backward direction in this zone. It is called backward slip zone. As the plate is drawn into the zone under the roller, it is pushed out of the backward slip zone and moves faster than the roller surface. This causes the relative slip of plate in the forward direction. This region is called forward slip zone.

Fig.5 Metal contact situation in zone of deformation
In order to handle such friction condition, an equivalent treatment of friction in plate rolling is presented, which is suitable for one-step forward calculation. As we know, when friction is in the opposite direction of displacement, the frictional work makes potential energy of the system increase, which results in the positive frictional work item in ![]() Contrarily, when friction is in the same direction of displacement, the frictional work item in
Contrarily, when friction is in the same direction of displacement, the frictional work item in ![]() is negative. Accordingly, for this case, the frictional work items in
is negative. Accordingly, for this case, the frictional work items in ![]() of the backward and forward slip zone are negative and positive, respectively. Then, the total frictional work of the whole process can be estimated by taking the contact history into account in terms of the position of boundary nodes in the final configuration.
of the backward and forward slip zone are negative and positive, respectively. Then, the total frictional work of the whole process can be estimated by taking the contact history into account in terms of the position of boundary nodes in the final configuration.
As shown in Fig.5, the zone between x0 and x2 is the deformation zone. Also, it is the frictional zone. The demarcation point of backward and forward slip zone is assumed to be the geometrical center of the frictional zone. As for nodal points of the final configuration in different zones, each equivalent frictional work is defined as follows.
1) x0≤x<x1,
![]() (22)
(22)
2) x1≤x<x2,
![]() (23)
(23)
3) x≥x2,
![]() (24)
(24)
where ![]() ,
, ![]() and
and ![]() represent actual frictional displacement, backward slip and forward slip displacement of contacted boundary nodal point respectively;
represent actual frictional displacement, backward slip and forward slip displacement of contacted boundary nodal point respectively; ![]() ,
, ![]() and
and ![]() represent actual contact boundary surface, backward slip and forward slip boundary surface, respectively.
represent actual contact boundary surface, backward slip and forward slip boundary surface, respectively.
By means of above simplified method, the frictional work considering the contact history is calculated reasonably, which is important in successful one-step simulation of plate rolling.
The rolling of flat plate is analyzed by one-step FE forward simulation. The width is negligible and such deformation problems can be considered to be in plain strain. The length and thickness of plate are 224 mm and 20 mm, respectively. It is reduced to a 10 mm in height by rolling through one roll stand. The radius of the roller is 175 mm. The material hardening behaviour is assumed to be ![]() The shear friction with a friction factor of f=0.3 is assumed between the roller and the plate. The cross section of the geometry is discretized by the four-node quadrilateral elements. There are 246 elements and 294 nodes in the FE models.
The shear friction with a friction factor of f=0.3 is assumed between the roller and the plate. The cross section of the geometry is discretized by the four-node quadrilateral elements. There are 246 elements and 294 nodes in the FE models.
Fig.6 presents the comparison of deformed meshes and equivalent stress distributions by one-step and incremental FE simulation, respectively. It can be seen that the deformed meshes and equivalent stress contours by one-step simulation are similar compared with those by incremental simulation. The error of equivalent stress extremum is 7.65%.
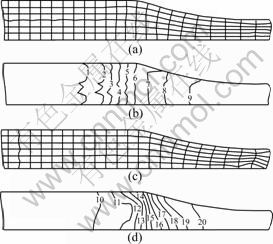
Fig.6 Comparison of deformed meshes and equivalent stress (MPa) contours obtained by one-step (a, b) and incremental (c, d) FE simulation for rolling of flat plate: 1—1.10; 2—1.92; 3—2.81; 4—3.74; 5—4.55; 6—5.48; 7—6.26; 8—7.19; 9—8.07; 10—0.92; 11—1.69; 12—2.46; 13—3.23; 14—4.01; 15—4.79; 16—5.55; 17—6.32; 18—7.09; 19—7.87; 20—8.64
For this plate rolling process, one-step computation also adopts one time step, whereas the incremental FE simulation involves 46 time steps under the static implicit FE software environment of ABAQUS/Standard. The time saving is considerable.
4 Conclusions
1) The bulk metal forming processes are simulated by using a one-step FE approach based on deformation theory of plasticity. This approach can give a reasonably accurate answer with less computational efforts compared with incremental FE approach.
2) One-step forward simulations for square rod compression and flat plate rolling processes are performed. Numerical simulation results by both one-step and incremental FE approach are compared, which verify the feasibility and validity of the proposed method.
References
[1] LEVY S, SHIN C F, WILKINSON J P D, STINE P, MCWILSON R C. Analysis of sheet metal forming to axisymmetric shapes [J]. Formability Topics—Metallic Materials, ASTM, 1978, 647: 238- 260.
[2] LEE C H, KOBAYASHI S. New solutions to rigid-plastic deformation problems using a matrix method [J]. Journal of Engineering for Industry, 1973, 95: 865-873.
[3] LIU Fang, SHAN De-bin, LU Yan. Experimental study and numerical simulation of isothermal closed die forging for aluminium alloy rotor [J]. Transactions of Nonferrous Metals Society of China, 2005, 15(4): 136-141.
[4] HODGE P G, WHITE G N. A quantitative comparison of flow and deformation theories of plasticity [J]. Journal of Applied Mechanics, 1950, 17(2): 180-184.
[5] CHUNG K, ALEXANDROV S. Ideal flow in plasticity [J]. Applied Mechanics Reviews, 2007, 60(11): 316-335.
[6] GUO Y Q, BSTOZ J L, DETRAUX P. Finite element procedures for strain estimations of sheet metal forming parts [J]. International Journal for Numerical Methods in Engineering, 1990, 30(8): 1385- 1401.
[7] MAJLESSI S A, LEE D. Deep drawing of square shaped sheet metal parts [J]. Journal of Engineering for Industry-Transactions of the ASME, 1993, 115:102-117.
[8] KIM S H, HUH H. Finite element inverse analysis for the design intermediate dies in multi-stage deep drawing processes with large aspect ratio [J]. Journal of Materials Processing Technology, 2001, 113: 779-785.
[9] CHUNG K, RICHMOND O. A deformation theory of plasticity based on minimum work paths [J]. International Journal of Plasticity, 1993, 9: 907-920.
[10] RICHMOND O, ALEXANDROV S. Nonsteady planar ideal plastic flow: General and special analytical solutions [J]. Journal of the Mechanics and Physics of Solids, 2000, 48: 1735-1759.
[11] CHUNG K, LEE W, RICHMOND O, ALEXANDROV S. Non-steady plane-strain ideal plastic flow [J]. International Journal of Plasticity, 2005, 21: 1322-1345.
[12] BOISSE P, BUSSY P, LADEVEZE P. A new approach in non linear mechanics: The large time increment method [J]. International Journal for Numerical Methods in Engineering, 1990, 29(3): 647- 663.
[13] ABDALI A, BENKRID K, BUSSY P. Simulation of sheet cutting by the large time increment method [J]. Journal of Materials Processing Technology, 1996, 60: 255-260.
[14] JOURDAN F, BUSSY P. Large time increment method in dynamic regularization: sheet cutting simulations [J]. Computer Methods in Applied Mechanics and Engineering, 2000, 190: 1245-1259.
[15] LIU Bao-sheng, LIU Yu. An preditermination method of tensorial time function in non-increment algorithm for forming process simulation [J]. Journal of Plasticity Engineering, 1999, 6(2): 17-25. (in Chinese)
[16] SIMO J C, ORTIZ M. A unified approach to finite deformation elastoplastic analysis based on the use of hyperelastic constitutive equations [J]. Computer Methods in Applied Mechanics and Engineering, 1985, 49: 221-245.
[17] BRUNIG M. Nonlinear finite element analysis based on a large strain deformation theory of plasticity [J]. Computers and Structures, 1998, 69: 117-128.
[18] WANG P, DONG X H, FU L J. One-step finite element simulation of upsetting processes based on deformation theory [C]// The 9th International Conference on Technology of Plasticity. Gyeongju, 2008: 1759-1764.
[19] WANG P, DONG X H, FU L J. Research on rapid simulation algorithm for bulk forming based on deformation theory [J]. Journal of Plasticity Engineering, 2008, 15(4): 72-76. (in Chinese)
Foundation item: Project(50575143) supported by the National Natural Science Foundation of China; Project(20040248005) supported by the Specialized Research Fund for the Doctoral Program of Higher Education of China
Corresponding author: WANG Peng; Tel: +86-21-62813435; E-mail: wpengw123@sjtu.edu.cn
DOI: 10.1016/S1003-6326(09)60134-5
(Edited by YANG Hua)

