文章编号:1004-0609(2014)06-1428-06
单斜晶体FeZn13、CoZn13和MnZn13弹性性质的第一性原理研究
米传同1, 2,刘国平1, 2,王家佳1, 2,郭新立1, 2,吴三械3,于 金1, 2
(1. 东南大学 材料科学与工程学院,南京 211189;
2. 东南大学 江苏省先进金属材料高技术研究重点实验室,南京 211189;
3. 南京大学 化学化工学院,南京 210093)
摘 要:采用基于密度泛函理论(DFT)的投影缀加波方法研究单斜晶体FeZn13、CoZn13和MnZn13的弹性性质和电子结构。利用应力-应变法结合广义梯度近似(GGA)和局域密度近似(LDA)计算3种单斜晶体的13个独立弹性常数;采用Voigt-Reuss-Hill模型计算得到多晶体的体积模量、切变模量和弹性模量。结果表明:采用GGA所得晶格参数与实验值吻合;基于GGA计算出FeZn13、CoZn13和MnZn13的弹性常数,并求得相应的体积模量、切变模量和弹性模量;计算所得FeZn13的弹性模量为103.7 GPa,与实验值基本吻合;同时,FeZn13与Zn两相之间弹性模量具有良好匹配性;FeZn13、CoZn13和MnZn13三者具有相近的弹性常数、弹性模量和相似的电子结构,且三者均满足单斜晶体的稳定性判据。
关键词:FeZn13;CoZn13;MnZn13;单斜晶体;第一性原理;弹性性能;电子结构
中图分类号:TG178 文献标志码:A
First-principle study on elastic properties of monoclinic FeZn13, CoZn13 and MnZn13
MI Chuan-tong1, 2, LIU Guo-ping1, 2, WANG Jia-jia1, 2, GUO Xin-li1, 2, WU San-xie3, YU Jin1, 2
(1. School of Materials Science and Engineering, Southeast University, Nanjing 211189, China;
2. Jiangsu Key Laboratory of Advanced Metallic Materials, Southeast University, Nanjing 211189, China;
3. School of Chemistry and Chemical Engineering, Nanjing University, Nanjing 210093, China)
Abstract: The elastic properties and electronic structures of FeZn13, CoZn13 and MnZn13 were studied by using first-principle based on the density functional theory (DFT). Stress-strain approach with the generalized gradient approximation (GGA) and local density approximation (LDA) was used to calculate the 13 independent elastic constants. The bulk modulus, shear modulus and elastic modulus were assessed through the Voigt-Reuss-Hill approximations. The results show that lattice constants calculated by GGA fit for the experimental values. The elastic constants of FeZn13, CoZn13 and MnZn13 were calculated by GGA, and the bulk modulus, shear modulus and elastic modulus were assessed from results through the Voigt-Reuss-Hill approximations. The calculated elastic modulus of FeZn13 is 103.7 GPa, which is identical with the experimental values. The elastic properties of FeZn13 can match well with that of Zn. The elastic constants, elasticity moduli and electronic structures of FeZn13, MnZn13 and CoZn13 are very close, and the elastic constants of them all satisfy stability conditions.
Key words: FeZn13; CoZn13; MnZn13; monoclinic crystal; first-principle; elastic property; electronic structure
热镀锌是目前应用最为广泛的钢铁防腐蚀技术,全世界生产的锌约50%用于热镀锌。热镀锌层中由外到内出现的中间相依次有η(Zn)、ζ(FeZn13)、δ(FeZn10)、Γ1(Fe5Zn21)、Γ(Fe3Zn10)相。这些相有不同的化学组 分、晶体结构和力学性能,对热镀锌层质量有较大影响。其中,ζ(FeZn13)相是热镀锌过程中一个非常重要的相[1-3]:1) 它是初生相,多生长为粗大的柱状结晶;2) 会影响与它临近的η相和δ相;3) 它属于单斜晶系,一般认为抗变形能力差,脆性较大。FeZn13相会在较大程度上影响整个热镀锌钢材的力学性能。弹性性质是结构材料重要的力学性能,第一性原理计算方法,能够在原子尺度上计算并揭示材料的弹性性能,且计算结果与实验值具有良好的一致性,目前已成为研究材料弹性性质的重要手段[4-5]。
目前,对FeZn13的研究报道不多,弹性性质仅REUMONT等[1]通过实验测得其弹性模量为117 GPa,而对其弹性常数、体弹性模量、剪切弹性模量等弹性性质,未见相关实验研究和计算研究。本文作者采用第一性原理计算方法研究单斜晶体FeZn13相的弹性性能,目前,仅见对单斜晶系α-Pu[6]和HfO2[7]的弹性性质研究报道。考虑Mn与Co在元素周期表中与Fe近邻,MnZn13、CoZn13和FeZn13都属于单斜晶系,在物理、化学性质上有很大的相似性[8-10],故还对MnZn13和CoZn13的弹性性质进行研究;利用计算出的弹性常数,采用稳定性判据对晶体结构进行稳定性分析;最后从电子结构对MnZn13、CoZn13和FeZn13弹性性质进行分析。
1 模型与计算方法
BROWN[11]、OSWALD等[12]、BELIN等[13]和LIU等[14]测得了FeZn13相的晶体结构。FeZn13相实验研究的困难在于难以制备出满足实验测试要求的样品。BROWN[11]利用从Zn含量超过99%(质量分数)的铸锭中电解提取的方法制备出FeZn13针状小晶体,并采用X射线衍射仪分析其晶体结构;OSWALD等[12]利用SPEX-8000 高能量球磨机,将一定比例的Fe和Zn粉末在氩气气氛中研磨,制备出FeZn13的机械合金粉末,并采用高分辨率中子粉末衍射仪测定其晶体结构;BELIN等[13]利用助溶剂法制备出FeZn13小单晶,并采用X射线衍射仪分析其晶体结构;LIU等[14]将满足FeZn13化学成分组成的Fe和Zn纯金属置于密封的石英管中,经高温液化后在水中进行淬火处理得到不足8 g的FeZn13多晶颗粒粉,然后利用X射线衍射技术结合Rietveld结构精修方法分析晶体结构,并利用陈氏晶格反演方法进行验证,两者吻合很好。比较发现, 他们的制样和测试方法在不断进步,晶体结构数据的测定越来越精确,如表1所列。
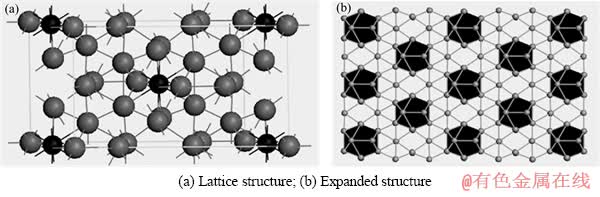
FeZn13属于单斜结构,其空间群为C2/m。本文作者利用LIU等[14]测得的结构构建模型,见图1(a)。 晶胞中含有28个原子,每个Fe原子和周围12个Zn原子相连,组成一个FeZn12正20面体,另一个Zn原子作为连接原子与另一个FeZn12成正20面体相连,构成FeZn13拓展结构,如图1(b)所示。根据BROWN[11]的实验结果,MnZn13和CoZn13的晶体结构与FeZn13的基本一致,只是晶格参数有所差异。
表1 FeZn13晶体结构测定的发展历程
Table 1 Development history of crystal structure determination of FeZn13

 —Fe
—Fe —Zn
—Zn
图1 FeZn13的晶体结构
Fig. 1 Crystal structures of FeZn13
本文作者利用基于DFT的VASP软件[15-16],采用经相对论校正的投影缀加波(PAW)[17-18]方法,并分别利用广义梯度近似(GGA)和局域密度近似(LDA)来处理交换关联能,弹性常数和电子结构均采用自旋极化方式。截断能选取500 eV,K点网格为5×5×7,收敛精度为1.0×10-6 eV。
弹性常数可以用6×6矩阵表示。由于晶体结构的对称性,单斜晶系独立的弹性常数减少为13个,如式(1)所示:
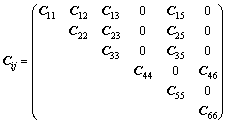 (1)
(1)
采用基于广义胡克定理的应力-应变法计算各晶体的弹性常数[19],弹性常数Cijkl与应力张量σij和应变张量δkl之间的关系可表示为
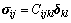 (2)
(2)
采用Hill模型通过弹性常数进一步得出晶体的体积模量(B)、切变模量(G)和弹性模量(E)。Hill模型考虑了Voigt模型和Reuss模型的计算结果分别会偏高和偏低的情况,将Voigt模型和Reuss模型的数值取算术平均值[20]。采用Voigt模型和Reuss模型计算单斜晶体体积模量(B)和切变模量(G)的公式[21]为
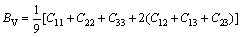 (3)
(3)
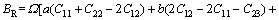

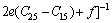 (4)
(4)
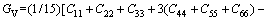
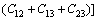 (5)
(5)
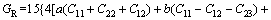


 (6)
(6)
其中:
 (7)
(7)
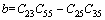 (8)
(8)
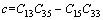 (9)
(9)
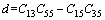 (10)
(10)
 (11)
(11)
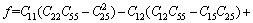
 (12)
(12)
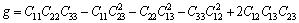 (13)
(13)
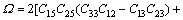


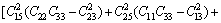
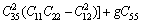 (14)
(14)
采用Hill模型计算单斜晶体体积模量(B)、切变模量(G)和弹性模量(E)的公式为
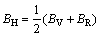 (15)
(15)
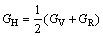 (16)
(16)
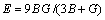 (17)
(17)
2 结果与讨论
2.1 晶体结构
表2 单斜FeZn13、CoZn13和MnZn13晶胞的平衡晶格常数
Table 2 Equilibrium lattice constants of monoclinic FeZn13, CoZn13 and MnZn13

利用GGA和LDA两种交换关联能近似方法对FeZn13、CoZn13和MnZn13进行几何优化,优化后的平衡晶格常数见表2。由表2可见,对于FeZn13,利用GGA方法优化后的结果与LIU等[14]所得实验值最大误差小于1%,而用LDA方法优化后的结果与LIU等[14]测得的实验值最大误差达到3.4%;对于CoZn13和MnZn13,利用GGA方法优化得到的结果与BROWN[11]的实验结果更为近似,所以,GGA方法更适用于FeZn13、CoZn13和MnZn13体系,优化晶格参数的结果更为准确。
2.2 弹性常数
利用结构充分弛豫的FeZn13、CoZn13和MnZn13的晶体结构计算弹性常数。采用GGA和LDA两种处理方法计算FeZn13、CoZn13和MnZn13的弹性常数,计算结果如表3所列;基于表3的弹性常数采用Hill模型计算出多晶体的体积模量(BH)、切变模量(GH)和弹性模量(EH),计算结果如表4所列。
计算所得FeZn13弹性常数(Cij)、体积模量(BH)、切变模量(GH)和弹性模量EH分别如表3和4所列。由表3和4可见,利用GGA和LDA两种方法得到的计算结果存在差异,利用GGA计算得到的FeZn13相弹性常数中的C11、C22和C33相比LDA方法的小40 GPa左右。对于不同类型的材料,处理交换关联能的方法对计算精度有一定影响。根据2.1节中GGA方法所得晶格参数与实验值吻合更好的事实,可以认为GGA方法所得弹性性质也较为准确。与实验值比较发现,FeZn13的弹性模量和实验值基本吻合。本文作者还利用GGA方法计算了Zn的弹性性质,计算结果以及文献实验报道见表4。由表4可见,FeZn13和Zn两相之间的弹性性质较为接近。
由此可知,热镀锌层中η相(Zn)与紧邻的次外层ζ相(FeZn13)构成的复合组织,其两相之间的弹性模量具有良好的匹配性。热镀锌之所以能够历经177 a的工业应用历史,且其应用如此广泛,是因为FeZn13与Zn两相之间弹性模量具有良好匹配性,是热镀锌构件持久耐用的重要保障之一。
FeZn13、CoZn13和MnZn13的弹性常数计算结果对比如表3所列。结果表明,这3种化合物的弹性常数非常接近;比较表4中3个相的多晶体体积模量(BH)、切变模量(GH)和弹性模量(EH)可知,其弹性模量也非常接近。这是由于同为单斜晶体的MnZn13、CoZn13和FeZn13在物理化学性质上具有相似性。这种相似性除了来源于3种化合物的结构相同外,还由于Fe、Mn和Co 3种过渡元素具有相邻的原子序数、相近的原子半径和电子数。
表3 采用GGA和LDA法计算的FeZn13、MnZn13和CoZn13的弹性常数
Table 3 Elastic constants of FeZn13, CoZn13 and MnZn13 calculated by GGA and LDA methods
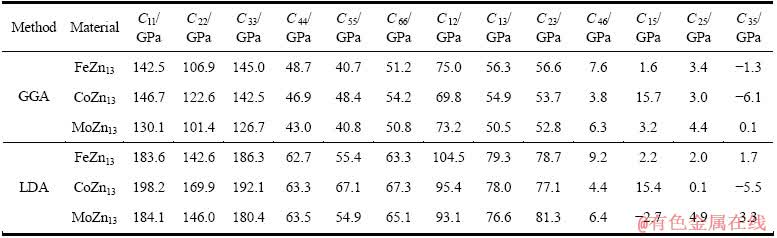
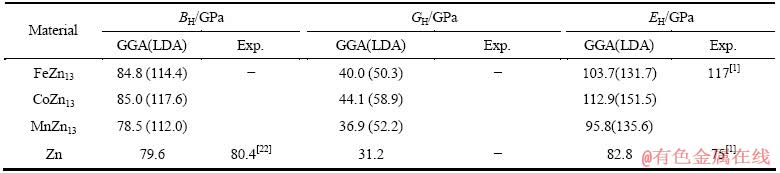
表4 采用Hill模型计算的FeZn13、CoZn13、MnZn13和Zn的体积模量(BH)、切变模量(GH)和弹性模量(EH)
Table 4 Bulk modulus (BH), shear modulus (GH) and elastic modulus (EH) of FeZn13, CoZn13, MnZn13 and Zn calculated by Hill model
2.3 稳定性分析
对于单斜晶体,其稳定性判据[23]为
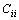 >0 (i=1, 2, 3, 4, 5, 6) (18)
>0 (i=1, 2, 3, 4, 5, 6) (18)
C11+C12+C33+2(C12+C13+C23)>0 (19)
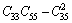 >0 (20)
>0 (20)
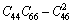 >0 (21)
>0 (21)
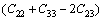 >0 (22)
>0 (22)
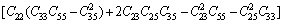 >0(23)
>0(23)
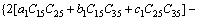
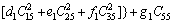 >0 (24)
>0 (24)
式中:
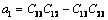 (25)
(25)
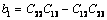 (26)
(26)
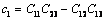 (27)
(27)
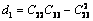 (28)
(28)
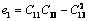 (29)
(29)
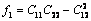 (30)
(30)
 (31)
(31)
经验证,FeZn13、CoZn13、MnZn13这3种化合物弹性常数均满足单斜晶体的稳定性判据。
2.4 电子结构
本文作者计算FeZn13、CoZn13和MnZn13的总态密度及Fe、Co、Mn和Zn的分波态密度,其结果如图2所示。由图2中可以看出,3种单斜晶体价带主要集中在-8.5~-6.5 eV低能段和-4~0 eV高能段。其中,低能段的贡献主要来源于Zn的3d电子,而高能段的贡献主要来源于Fe、Co和Mn的3d电子。3种化合物导带也主要是Fe、Co和Mn的3d电子的贡献。由于Zn本身没有磁性,所以,这3种化合物的磁性分别由Fe、Co和Mn提供。其中,CoZn13的总态密度和分波态密度都十分对称,说明它基本没有磁性;FeZn13和MnZn13的总态密度对称性稍差,呈现微弱的磁性,这主要来源于Fe和Mn的3d电子的作用。总体上此3种化合物在电子结构上具有很大的相似性。
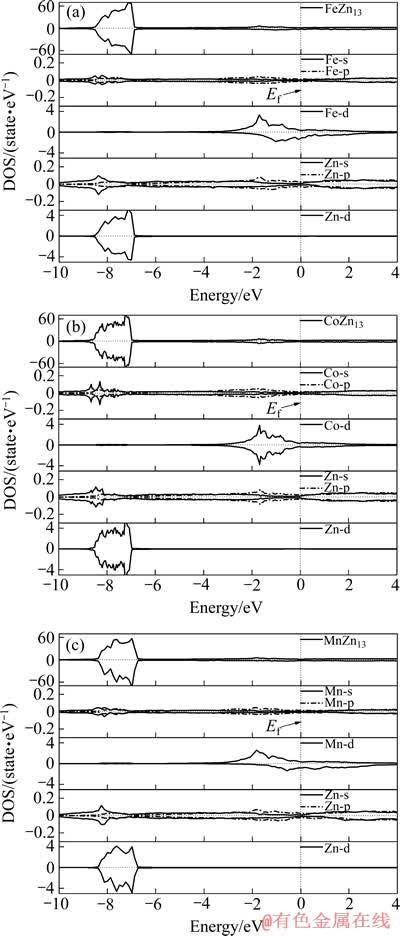
图2 FeZn13、CoZn13和MnZn13的总态密度和分波态密度
Fig. 2 Total and partial density of states of FeZn13(a), CoZn13(b) and MnZn13(c)
3 结论
1) 采用基于密度泛函理论的第一性原理,研究FeZn13和CoZn13、MnZn13的晶体结构、弹性性质和电子结构。
2) 采用GGA所得晶格参数与实验值吻合更好。
3) 基于GGA计算出FeZn13、CoZn13和MnZn13的弹性常数、体积模量、切变模量和弹性模量;计算所得FeZn13的弹性模量与实验值基本吻合;同时,FeZn13与Zn两相之间弹性模量具有良好的匹配性。
4) FeZn13、CoZn13和MnZn13三者具有相近的弹性常数、弹性模量和相似的电子结构,且三者均满足单斜晶体的稳定性判据。
REFERENCES
[1] REUMONT G, VOIGT J B, IOST A, FOCT J. The effects of an Fe-Zn intermetallic-containing coating on the stress corrosion cracking behavior of a hot-dip galvanized steel[J]. J Surf Coat Technol, 2001, 139(2/3): 265-271.
[2] MARDER A R. The metallurgy of zinc-coated steel[J]. Prog Mater Sci, 2000, 45(3): 191-271.
[3] ZHU W H, JIN H M, WU P, LIU H L. Periodic density functional theory study of the crystal morphology of FeZn13[J]. Phys Rev B, 2004, 70(16): 165419-1-5.
[4] 陈捷狮, 曾 含, 王 路, 蓝志强, 郭 进. 过渡金属对Mg2Ni氢化物电子结构和热力学稳定性影响: 第一性原理研究[J]. 中国有色金属学报, 2012, 22(1): 216-223.
CHEN Jie-shi, ZENG Han, WANG Lu, LAN Zhi-qiang, GUO Jing. Effects of transitional metal on electronic structure and thermodynamic stability of Mg2Ni hydride: A first principle investigation[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(1): 216-223.
[5] PAN L X, XIA Q L, YE S L, DING N, LIU Z R. First principles study of electronic structure, chemical bonding and elastic properties of BiOCuS[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(5): 1197-1202.
[6] SODERLIND P, KLEPEIS J E. First-principles elastic properties of α-Pu[J]. Phys Rev B, 2009, 79(10): 104110-1-6.
[7] WU R, ZHOU B, LI Q, JIANG Z Y, WANG W B, MA W Y, ZHANG X D. Elastic and vibrational properties of monoclinic HfO2from first-principles study[J]. J Phys D: Appl Phys, 2012, 45(12): 125304-1-7.
[8] SYLLA D, CREUS J, SAVALL C, ROGGY O, GADOULEAU M, REFAIT P. Electrodeposition of Zn-Mn alloys on steel from acidic Zn-Mn chloride solutions[J]. Thin Solid Films, 2003, 424(2): 171-178.
[9] RAGHAVAN V. Cr-Fe-Zn (chromium-iron-zinc)[J]. J Phase Equilib Diffus, 2008, 29(5): 442-443.
[10] RAGHAVAN V. Al-Fe-Mn-Zn (aluminum-iron-manganese- zinc)[J]. J Phase Equilib Diffus, 2011, 32(4): 384-385.
[11] BROWN P J. The structure of the ζ-phase in the transition metal-zinc alloy systems[J]. Acta Cryst, 1962, 15(6): 608-612.
[12] OSWALD N C, UWAKWEH, LIU Z T, JORDAN A, BRYAN C, STEPHEN S, PHILIP M. Nentron diffraction and phase evolution of the mechanically alloyed intermetallic compound ζ-FeZn13[J].. Metall Mater Trans A, 1996, 31(11): 2739-2745.
[13] BELIN R, TILLARD M, MONCONDUIT L. Redetermination of the iron-zinc phase FeZn13[J]. Acta Cryst C, 2000, 56(3): 267-268.
[14] LIU Y, SU X P, YIN F C, LI Z, LIU Y H. Experimental determination and atomistic simulation on the structure of FeZn13[J]. J Phase Equilib Diffus, 2008, 29(6): 488-492.
[15] HAFNER J. Ab-initiosimulations of materials using VASP: Density-functional theory and beyond[J]. J Comput Chem, 2008, 29(13): 2044-2078.
[16] KRESSE G. Efficient iterative schemes for ab initio total—Energy calculations using a plane-wave basis set[J]. J Phys Rev B, 1996, 54(16): 11169-11186.
[17] TORRENT M, JOLLET F, BOTTIN F. Implementation of the projector augmented-wave method in the ABINIT code: Application to the study of iron under pressure[J]. Computational Materials Science, 2008, 42(2): 337-351.
[18] KRESSE G, JOUBERT D. From ultrasoft pseudopotentials to the projector augmented-wave method[J]. Physical Review B, 1999, 59(3): 1758-1775.
[19] MEHL M J, OSBURN J E, PAPACONSTANTOPOULOS D A, KLEIN B M. Structural properties of ordered high-melting- temperature intermetallic alloys from first-principles total-energy calculations[J]. Phys Rev B, 1990, 41(15): 10311-1-3.
[20] PANDA K B, RAVI CHANDRAN K S. Determination of elastic constants of titanium diboride (TiB2) from first principles using FLAPW implementation of the density functional theory[J]. Comput Mater Sci, 2006, 35(2): 134-150.
[21] WU Z J, ZHAO E J, XIANG H P, HAO X F, LIU X J, MENG J. Crystal structures and elastic properties of superhard IrN2and IrN3from first principles[J]. Phys Rev B, 2007, 76(5): 054115-1-5.
[22] SIMMONS G, WANG H. Single crystal elastic constant and calculated aggregate properties: A handbook[M]. Cambridge: MIT Press, 1971: 134-135.
[23] GRIMVALL G, BLANKA M K, VIDVUDS O, KRISTIN A P. Lattice instabilities in metallic elements[J]. Rev Mod Phys, 2012, 84(2): 945-986.
(编辑 陈卫萍)
基金项目:国家自然科学基金资助项目( 21173041)
收稿日期:2013-09-13;修订日期:2014-02-25
通信作者:于 金,教授,博士;电话:025-82089129;E-mail: yujin@seu.edu.cn