DOI: 10.11817/j.issn.1672-7207.2016.07.041
大跨屋盖结构多目标等效静力风荷载精细化分析
李玉学1, 2,杨庆山3,田玉基3,朱英磊1, 2
(1. 石家庄铁道大学 土木工程学院,河北 石家庄,050043;
2. 石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室,河北 石家庄,050043;
3. 北京交通大学 土木建筑工程学院结构风工程与城市风环境北京市重点实验室,北京,100044)
摘要:基于已建立的大跨屋盖结构多目标等效静力风荷载理论框架,对其中存在的关键问题进行精细化分析。首先,根据结构风振响应特性,分别推导构造多目标等效静力风荷载的背景分量、共振分量及其二者耦合项分量,解决基本分量应与风振响应分析结果相对应且能再现风振响应特性的问题。其次,根据各基本分量作用下结构静力响应分布的相似程度对基本分量进行归并精简,从而保证所选基本分量的高效性,实现用较少的基本分量完成尽可能多的目标响应等效。最后,针对基于数值方法求解多目标等效方程造成的计算结果离散性大、不便于工程应用、精度不高等问题,补充求解的边界条件方程,并提出对计算结果的修正方法。利用提出的精细化分析方法,对国家网球中心“莲花”球场屋盖结构多目标等效静力风荷载进行分析。研究结果表明:所得多目标等效静力风荷载分布合理,静力响应与多目标响应较吻合,验证了所提出的方法的有效性和工程实用性。
关键词:大跨屋盖;等效静力风荷载;多目标;基本荷载分量;精细化分析
中图分类号:TU393.3;TU312 文献标志码:A 文章编号:1672-7207(2016)07-2485-10
Refinement analysis of multi-target equivalent static wind loads for large-span roofs
LI Yuxue1, 2, YANG Qingshan3, TIAN Yuji3, ZHU Yinglei1, 2
(1. School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;
2. Key Laboratory of Roads and Railway Engineering Safety Control of Ministry of Education,
Shijiazhuang 050043, China;
3. Beijing’s Key Laboratory of Structural Wind Engineering and Urban Wind Environment,
School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China)
Abstract: According to the critical problems existing in the theoretical framework for multi-target equivalent static wind loads (ESWLs) analysis, a refinement method was proposed to obtain the multi-target ESWLs of large-span roofs. Firstly, considering the characteristics of wind-induced response, the background, resonant and their coupling fundamental load vectors used to establish the multi-target ESWLs were derived, which well solved the problems that the fundamental load
vectors should be corresponded to the wind-induced response results and the multi-target ESWLs should reexhibit the characteristics of wind-induced response. Then, based on the distribution similarity of the static responses excited by the fundamental load vectors, a merging method for the fundamental load vectors was proposed, which can well ensure the efficiency of the selected fundamental load vectors, and thus using less fundamental load vectors accomplished more targets equivalence. At last, a boundary condition equation and a modified equation were introduced, which well solved the problems of the calculation results including high discreteness, low accuracy and inconvenient engineering application induced by numerical calculation. The proposed refinement method was applied in the National Tennis Center Stadium roof. The results show that the obtained multi-target ESWLs distribution is reasonable and the static responses excited by the multi-target ESWLs agrees well with the target responses.
Key words: large-span roof; equivalent static wind loads; multi-target; fundamental load vectors; refinement analysis
等效静力风荷载的概念自DAVENPORT[1]提出以来便得到人们的广泛关注并不断发展。目前,针对单个目标响应的等效静力风荷载分析方法已经趋于成熟,形成了阵风荷载因子法、惯性力法以及荷载响应相关法等多种分析方法[2-4],较好地解决了高层、高耸这类形式简单、风振响应控制模态单一的结构等效静力风荷载计算问题[5-7]。对于大跨屋盖结构,其结构形式和表面风荷载均非常复杂,且风振响应需要考虑多阶模态参与,使得不同位置的响应不再在同一时刻达到极值,上述针对单目标(某一位置)响应得到的等效静力风荷载,不能保证其他位置响应极值等效。针对这一问题,国内外许多学者进行了研究,如:KATSUMURA等[8]将脉动风荷载的本征模态作为等效静力风荷载的基本分布模式,采用最小二乘法计算其最优组合系数,从而满足多个目标响应等效;TAMURA等[9-10]根据不同等效目标得到的多组等效静力风荷载取平均值和取包络线作为多目标等效静力风荷载;杨庆山等[11]将等效静力风荷载分为背景分量和共振分量,分别以脉动风荷载主要本征模态和主导振型惯性力作为其基本分量,从而构造并求解满足多个响应目标的等效静力风荷载方程;ZHOU等[12]通过修正LRC(load response correlation)法同时考虑等效静力风荷载背景分量和共振分量,并利用响应分组通过数值求解得到多目标等效静力风荷载;罗楠等[13]以广义恢复力的本征模态作为基本向量,基于最小二乘原理计算得到了时域内多目标等效静力风荷载。上述研究在一定程度上解决了大跨屋盖结构风振响应多目标静力等效问题,并逐步形成了完整的分析理论框架,即首先选取构造多目标等效静力风荷载的基本分量,然后采用数学方法寻求其统计意义上最优的组合系数,据此组合得到能够最大限度地兼顾多个目标响应的等效静力风荷载。这一理论框架为大跨屋盖结构等效静力风荷载的计算提供了清晰思路,但在实际操作过程中还有一些关键问题需要进行深入研究,主要包括:1) 等效静力风荷载的计算需要基于风振响应分析结果,如何使得所选基本分量与风振响应分析结果相对应,这是保证所求多目标等效静力风荷载能够再现风振响应特性且具有明确物理意义的关键;2) 力争选取较少的基本分量实现尽可能多的目标响应等效,这对于提高多目标等效静力风荷载计算效率非常关键;3) 多目标等效方程的求解需要借助数值方法,如何保证其计算精度并方便工程应用需要深入研究。本文作者将针对上述关键问题进行精细化分析,以提出相应的解决思路。
1 多目标等效静力风荷载理论框架
大跨屋盖结构多目标等效静力风荷载理论框架主要分析步骤如下。
1) 首先选定构造多目标等效静力风荷载的基本分量,并对其进行组合:
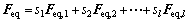 (1)
(1)
式中:Feq为构造的多目标等效静力风荷载;元素Feq,j和sj分别为选定的第j个荷载基本分量与其组合系数;l为基本分量的数量。
2) 从等效静力风荷载的基本概念出发,建立多目标等效静力风荷载作用下结构静力响应与目标响应间的等效方程组。
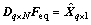 (2)
(2)
式中: ,为结构响应影响系数矩阵;元素Dj为第j个目标响应的影响系数N维列向量;N为结构节点数量;q为结构目标响应数量;
,为结构响应影响系数矩阵;元素Dj为第j个目标响应的影响系数N维列向量;N为结构节点数量;q为结构目标响应数量; 为结构q个目标响应组成的列向量,其中元素
为结构q个目标响应组成的列向量,其中元素 为第j个目标响应。
为第j个目标响应。
3)采用数值方法对等效方程组(2)进行求解,由于式(2)是1个以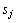 为未知数的非齐次方程组,未知数的个数为l,即所选定的基本分量的数量,而方程的个数为q,即结构目标响应的数量。如前所述,对于大跨屋盖结构,所关心的目标响应常常很多,在大多数情况下,q>l。由线性代数中线性方程组的求解原理可知,此时一般只能得到
为未知数的非齐次方程组,未知数的个数为l,即所选定的基本分量的数量,而方程的个数为q,即结构目标响应的数量。如前所述,对于大跨屋盖结构,所关心的目标响应常常很多,在大多数情况下,q>l。由线性代数中线性方程组的求解原理可知,此时一般只能得到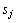 的最小二乘解
的最小二乘解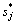 ,将其代入式(1)便得到多目标等效静力风荷载:
,将其代入式(1)便得到多目标等效静力风荷载:
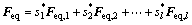 (3)
(3)
至此,得到的等效静力风荷载Feq能够保证结构静力响应与等效目标的实际动力响应极值间误差 最小。
要据此理论框架求解大跨屋盖结构的多目标等效静力风荷载,需要合理选定基本分量Feq, j及其数量l,同时还需保证式(3)得到的Feq能够与结构自重、其他活载等方便组合,并满足工程精度要求。
2 多目标等效静力风荷载基本分量选取
按照等效静力风荷载基本分量应与风振响应分析结果相对应,并能够反映和再现风振响应特性的原则,本文针对构成总风振响应的背景分量、共振分量及二者的耦合项分别给出其相对应的等效静力风荷载,作为构造多目标等效静力风荷载的基本分量。
大跨屋盖结构在脉动风荷载作用下的运动方程为
 (4)
(4)
式中:M,C和K分别为结构的质量、阻尼和刚度矩阵;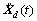 ,
,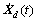 和
和 分别为加速度、速度和位移向量;
分别为加速度、速度和位移向量;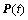 为测压点处的脉动风荷载列向量;L为测压点与节点间等效力转换矩阵。根据模态分解理论,并按照文献[14]选取m阶主导模态参与计算。为提高计算精度,利用模态加速度法基本原理[15],将剩余的
为测压点处的脉动风荷载列向量;L为测压点与节点间等效力转换矩阵。根据模态分解理论,并按照文献[14]选取m阶主导模态参与计算。为提高计算精度,利用模态加速度法基本原理[15],将剩余的 阶非主导模态对结构响应的贡献进行补偿(n为总模态阶数),则式(4)中的位移响应可表示为
阶非主导模态对结构响应的贡献进行补偿(n为总模态阶数),则式(4)中的位移响应可表示为
 (5)
(5)
式中: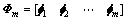 ,为m阶主导模态组成的模态矩阵,元素
,为m阶主导模态组成的模态矩阵,元素 为第j阶模态的模态向量;
为第j阶模态的模态向量;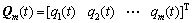 ,为m阶主导模态坐标组成的列向量,元素
,为m阶主导模态坐标组成的列向量,元素 为结构第j阶模态坐标;
为结构第j阶模态坐标; ,元素
,元素 为结构第j阶模态的圆频率;
为结构第j阶模态的圆频率; 表示对角矩阵;
表示对角矩阵; 表示补偿的
表示补偿的 阶非主导模态对结构响应的贡献(不同于模态加速法补偿被截断高阶模态对结构响应的贡献[15])。
阶非主导模态对结构响应的贡献(不同于模态加速法补偿被截断高阶模态对结构响应的贡献[15])。
将式(5)进一步变形表示为

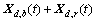 (6)
(6)
由背景响应和共振响应的概念[16],式(6)右边第1项和第2项(中括号部分)分别为t时刻位移响应的瞬时背景分量和瞬时共振分量。
按照随机振动理论,由式(6)可以得到结构某一自由度i上的总响应方差:
 (7)
(7)
式中: 和
和 分别为由
分别为由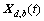 和
和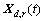 得到的结构第i自由度上背景响应方差和共振响应方差;
得到的结构第i自由度上背景响应方差和共振响应方差; 为二者的相关系数,表征其耦合效应。
为二者的相关系数,表征其耦合效应。
基于式(7)风振响应分析结果,可以分别得到风振响应背景、共振及其二者耦合项对应的等效静力风荷载基本分量。
2.1 等效静力风荷载背景分量
将式(6)中的瞬时背景分量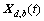 变形为
变形为

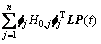 (8)
(8)
式中: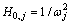 ,为矩阵
,为矩阵 中元素。由式(8)可得背景分量
中元素。由式(8)可得背景分量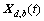 的自相关函数矩阵:
的自相关函数矩阵:

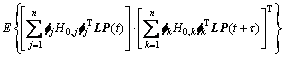
(9)
式中: 表示数学期望;
表示数学期望;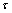 为虚时间变量。
为虚时间变量。
根据式(9),由方差与谱密度的关系及维纳-辛钦关系可得背景响应方差矩阵:
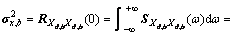
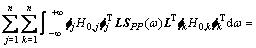
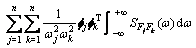 (10)
(10)
式中: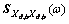 和
和 分别为背景响应功率谱矩阵和脉动风荷载功率谱矩阵;
分别为背景响应功率谱矩阵和脉动风荷载功率谱矩阵;
 为第j和第k阶模态力互谱。
为第j和第k阶模态力互谱。
取式(10)中对角线元素可以得到结构某一自由度i上背景响应均方差:
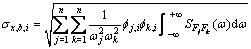 (11)
(11)
式中: 和
和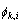 分别为第j和第k阶模态在结构第i自由度上的值。
分别为第j和第k阶模态在结构第i自由度上的值。
由式(6)及荷载与响应关系,可得结构响应瞬时等效静力风荷载背景分量 的方差矩阵:
的方差矩阵:
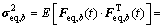

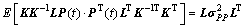 (12)
(12)
式由式(11)和(12)中得到的 和
和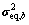 ,根据LRC法原理[4],可得与式(7)相对应,保证结构第i自由度上背景响应极值相等的等效静力风荷载:
,根据LRC法原理[4],可得与式(7)相对应,保证结构第i自由度上背景响应极值相等的等效静力风荷载:
 (13)
(13)
式中:Di为结构第i自由度上位移响应的影响系数向量;gb为背景响应的峰值因子,可以根据极值穿越理论求得[3]。
2.2 等效静力风荷载共振分量
将式(6)中瞬时共振分量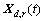 变形表示为
变形表示为

 (14)
(14)
由式(14)可得共振分量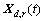 的自相关函数矩阵:
的自相关函数矩阵:

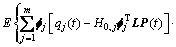
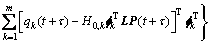 (15)
(15)
根据式(15),由方差与谱密度的关系及维纳 -辛钦关系可得共振响应方差矩阵:

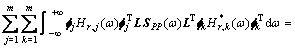
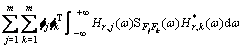 (16)
(16)
式中: 为共振响应功率谱矩阵;
为共振响应功率谱矩阵;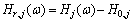 为第j阶模态共振响应频响函数;
为第j阶模态共振响应频响函数; 为第j阶模态频响函数;
为第j阶模态频响函数;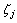 为第j阶模态阻尼比;i为虚数单位;“
为第j阶模态阻尼比;i为虚数单位;“ ”表示复数取共轭。
”表示复数取共轭。
取式(16)中对角线元素可以得到结构某一自由度i上共振响应均方差:
 (17)
(17)
由式(6)及荷载与响应的关系,可得结构响应瞬时等效静力风荷载共振分量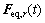 的方差矩阵:
的方差矩阵:




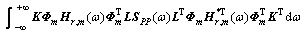 (18)
(18)
式中: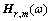 为由元素
为由元素 组成的对角矩阵,
组成的对角矩阵, 。
。
由式(17)和(18)中得到的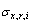 和
和 ,根据LRC法原理[4],可得与式(7)相对应、保证结构第i自由度上共振响应极值相等的等效静力风荷载:
,根据LRC法原理[4],可得与式(7)相对应、保证结构第i自由度上共振响应极值相等的等效静力风荷载:
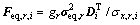 (19)
(19)
式中:gr为共振响应的峰值因子,可以根据极值穿越理论求得[3]。
2.3 等效静力风荷载背景和共振耦合项分量
为了与式(14)中的共振分量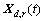 相对应,对式(8)表示的背景分量
相对应,对式(8)表示的背景分量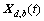 只考虑主导模态,则可得二者耦合项互相关函数矩阵:
只考虑主导模态,则可得二者耦合项互相关函数矩阵:

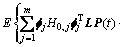
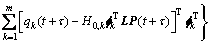 (20)
(20)
由式(20),根据方差与谱密度的关系及维纳-辛钦关系可得背景、共振耦合项方差矩阵:


 (21)
(21)
取式(21)中对角线元素可以得到结构某一自由度i上的背景、共振响应耦合项均方差:

(22)
由式(6)及荷载与响应的关系,可得结构响应瞬时背景、共振耦合项等效静力风荷载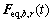 的协方差矩阵:
的协方差矩阵:
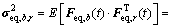


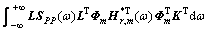 (23)
(23)
由式(22)和(23)中得到的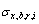 和
和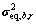 ,根据LRC法原理[4],可得与式(7)相对应、保证结构第i自由度上背景、共振响应耦合项极值相等的等效静力风荷载:
,根据LRC法原理[4],可得与式(7)相对应、保证结构第i自由度上背景、共振响应耦合项极值相等的等效静力风荷载:
 (24)
(24)
式中: 为背景、共振响应耦合项的峰值因子,可以根据极值穿越理论求得[3]。
为背景、共振响应耦合项的峰值因子,可以根据极值穿越理论求得[3]。
2.4 等效静力风荷载基本分量归并精简
保证所选荷载基本分量的有效性是提高多目标等效静力风荷载计算效率的关键。根据前面求得的等效静力风荷载基本分量作用下结构静力响应分布相似程度,分别对其进行归并精简,使得所选基本分量更加高效,以实现用较少的基本分量完成尽可能多的目标响应等效,提高计算效率。
以背景响应等效静力风荷载基本分量 (i=1, 2, 3, …, l ,l 为2.1节按初选得到的背景响应等效静力风荷载基本分量数量)为例,其具体处理过程如下。
(i=1, 2, 3, …, l ,l 为2.1节按初选得到的背景响应等效静力风荷载基本分量数量)为例,其具体处理过程如下。
1) 计算在背景响应等效静力风荷载基本分量 作用下的结构静力响应
作用下的结构静力响应 :
:
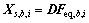 (25)
(25)
式中:D为结构响应的影响系数矩阵。
2) 根据静力响应向量
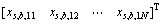 (N为结构节点数量)归并精简与
(N为结构节点数量)归并精简与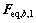 特性近似的背景响应等效静力风荷载基本分量:
特性近似的背景响应等效静力风荷载基本分量:
(ⅰ)将静力响应向量
 在静力响应向量
在静力响应向量
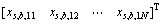 上投影,得向量
上投影,得向量 :
:
 (26)
(26)
根据向量的几何特性,向量 与向量
与向量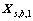 正交,即
正交,即
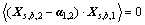 (27)
(27)
式中:符号 表示向量做内积。将式(26)代入式(27)得
表示向量做内积。将式(26)代入式(27)得
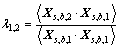 (28)
(28)
式中: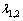 定义为
定义为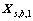 和
和 的相关系数,且有
的相关系数,且有 ,其值可反映
,其值可反映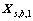 和
和 分布相似程度,其相似度越高,说明所对应的荷载基本分量
分布相似程度,其相似度越高,说明所对应的荷载基本分量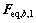 与
与 特性越接近,据此可将其归并。
特性越接近,据此可将其归并。
(ⅱ) 按照(ⅰ)中方法分别求得 ,
, ,…,
,…,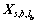 对应的相关系数
对应的相关系数 ,
,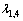 ,…,
,…, 。
。
(ⅲ) 将 ,
,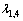 ,…,
,…, 从小到大依次排序,其中
从小到大依次排序,其中 (i≥2)越大的静力响应向量
(i≥2)越大的静力响应向量 与
与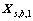 相似度越高。根据需要,如限定
相似度越高。根据需要,如限定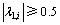 ,将与
,将与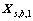 相似度高的静力响应向量所对应的背景响应等效静力风荷载基本分量与
相似度高的静力响应向量所对应的背景响应等效静力风荷载基本分量与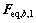 归并。
归并。
为方便编程计算,将特性接近的荷载基本分量归并精简后,剩余的荷载基本分量编号仍保持不变。
3) 根据静力响应向量
 (N为结构节点数目)归并精简成与
(N为结构节点数目)归并精简成与 特性接近的背景响应等效静力风荷载基本分量(需要说明的是,若
特性接近的背景响应等效静力风荷载基本分量(需要说明的是,若 对应的
对应的 已经被归并,则自动跳过该编号)。
已经被归并,则自动跳过该编号)。
按照2)中方法分别计算 与后面剩余向量
与后面剩余向量 (i≥3)的相关系数
(i≥3)的相关系数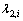 ( i≥3),并对其从小到大依次排序,其中
( i≥3),并对其从小到大依次排序,其中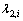 ( i≥3)越大的向量
( i≥3)越大的向量 与
与 相似度越高。根据需要,如限定
相似度越高。根据需要,如限定 ,将与
,将与 相似度高的静力响应向量所对应的背景响应等效静力风荷载基本分量与
相似度高的静力响应向量所对应的背景响应等效静力风荷载基本分量与 进行归并。
进行归并。
4) 分别根据静力响应向量 ,
, ,…,
,…,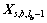 归并成与
归并成与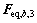 ,
, ,…,
,…,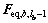 特性接近的背景响应等效静力风荷载基本分量(同样,若其中某个基本分量已经被归并,则自动跳过该编号)。
特性接近的背景响应等效静力风荷载基本分量(同样,若其中某个基本分量已经被归并,则自动跳过该编号)。
5) 将步骤2)~4)中归并后剩余的基本分量进行整理,作为最终选定的背景响应等效静力风荷载基本分量,记为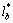 。
。
将以上过程程序化,可以方便实现背景响应等效静力风荷载基本分量的归并精简,按照同样的思路分别对共振响应等效静力风荷载基本分量以及背景、共振耦合项等效静力风荷载基本分量进行归并精简。
3 多目标等效静力风荷载的修正
按照前面方法选定构造多目标等效静力风荷载的各基本分量后,就可以由式(2)计算其组合系数。
实际计算表明,按照式(2)求得的多目标等效静力风荷载虽然能够保证结构静力响应与目标响应间误差最小,但由于式(2)求解基于纯粹的数值方法,使得所求等效静力风荷载往往离散性较大,会出现部分节点处等效静力风荷载达到数十甚至数千帕,以至于在结构设计时无法与自重、其他活载等进行组合,给工程应用带来不便。为此,本文结合大跨屋盖结构表面风荷载特性,增加式(2)求解的边界条件方程:
 (29)
(29)
式中: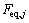 为荷载向量
为荷载向量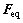 中与结构第j个节点对应的元素;
中与结构第j个节点对应的元素; 为结构第j个节点上脉动风荷载的均方差;
为结构第j个节点上脉动风荷载的均方差;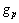 为脉动风荷载的峰值因子,可以根据极值穿越理论求得[3]。
为脉动风荷载的峰值因子,可以根据极值穿越理论求得[3]。
式(29)是根据结构实际作用的脉动风荷载极值对所求多目标等效静力风荷载数值进行限制,因此,对式(2)增加求解的边界条件式(29)后,所得多目标等效静力风荷载数值离散性降低,实现了与结构自重、其他活载等方便组合,但相比直接由式(2)求得的多目标等效静力风荷载,其对应的静力响应计算精度降低。为了提高精度,本文将对所求得的多目标等效静力风荷载进行修正。
由式(2)和(29)求得的多目标等效静力风荷载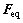 作用下结构静力响应为
作用下结构静力响应为
 (30)
(30)
目标响应与静力响应间的误差为
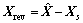 (31)
(31)
式中: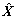 为目标响应向量。
为目标响应向量。
由结构静力响应与等效静力风荷载间的关系得
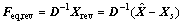 (32)
(32)
式中: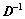 为矩阵D的广义逆。由式(32)可得多目标等效静力风荷载
为矩阵D的广义逆。由式(32)可得多目标等效静力风荷载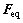 中第j个元素的修正系数:
中第j个元素的修正系数:
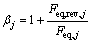 (33)
(33)
式中: 和
和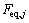 分别为向量
分别为向量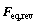 和
和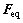 中第j个元素。
中第j个元素。
至此,经修正后的多目标等效静力风荷载可以表示为
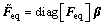 (34)
(34)
式中: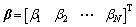 ,为由修正系数
,为由修正系数 组成的等效静力风荷载修正系数向量。
组成的等效静力风荷载修正系数向量。
4 多目标等效静力风荷载精细化求解步骤
基于已经建立的理论框架,按照本文提出的精细化分析方法,大跨屋盖结构多目标等效静力风荷载计算主要步骤如下。
1) 分别按照式(13),(19)和(24)计算构造多目标等效静力风荷载的基本分量 ,
, 和
和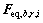 ,并按照2.4节中的方法对其进行归并精简,最终确定各荷载基本分量及其数量
,并按照2.4节中的方法对其进行归并精简,最终确定各荷载基本分量及其数量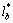 ,
, 和
和 。
。
2) 将归并精简后最终选定的等效静力风荷载基本分量按照式(1)进行组合:


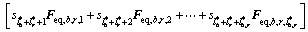 (35)
(35)
3) 将式(35)代入式(2),并结合边界条件方程式(29)对其进行求解,求得最优组合系数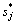 。据此系数
。据此系数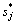 ,按照式(3)组合得到多目标等效静力风荷载
,按照式(3)组合得到多目标等效静力风荷载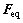 。
。
4)为提高计算精度,根据式(33)计算多目标等效静力风荷载的修正系数 ,最终由式(34)得到修正后的多目标等效静力风荷载
,最终由式(34)得到修正后的多目标等效静力风荷载 。
。
5 算例分析
根据大跨屋盖结构多目标等效静力风荷载精细化求解方法,采用FORTRAN语言编制计算程序,以国家网球中心“莲花”球场屋盖结构为例,采用本文方法计算其多目标等效静力风荷载,并对所得多目标等效静力风荷载作用下结构静力响应与目标响应进行对比分析,以检验所提方法的适用性。
国家网球中心“莲花”球场为12个“Z”形花瓣单元组成的环形结构,底部直径为79.7 m,并坐落在高6.0 m的平台上,平台、看台结构和21.6 m长的看台挑棚共同组成1个“Z”字形,各“Z”字形单元之间开有较大洞口,整体形成“莲花”的特殊造型,如图1所示。为了排水需要,挑棚设有大约3°的倾角,挑棚前檐最高点标高23.0 m。挑棚结构形状特殊,钝体绕流特征明显,属于风敏感结构。现行风荷载规范没有提供其抗风设计所需的风荷载,需借助风洞试验获取。

图1 国家网球中心“莲花”球场
Fig. 1 “Lianhua” stadium of national tennis center
5.1 结构风洞试验与风振响应分析
国家网球中心“莲花”球场屋盖模型风洞试验在北京大学力学与工程科学系直径为2.25 m的大型低速风洞中完成,用ABS材料和有机玻璃制作屋盖刚性测压模型,模型缩尺比为1:120,地面粗糙度取B类,采用的名义风速为15 m/s。考虑结构的对称性,仅在模型的第3和第4单元上、下表面各布置78个测压点,每个测压点采样点数为3 900,采样频率为400 Hz,并将上、下表面测得风荷载进行叠加,其中试验模型、单元编号及测点布置如图2所示。为了获得特定风向角下整个模型(12个单元)的风荷载,共进行18个风向角的测压试验,本算例分析选取0°风向角时的测压,主要风向角定义如图3所示。

图2 风洞试验模型及测点布置
Fig. 2 Model for wind tunnel test and pressure taps arrangement

图3 典型控制节点位置编号及风洞试验中风向角
Fig. 3 Key nodes number and wind angle of experimental model
为了得到结构动力特性参数进行风振响应计算,在SAP2000中建立结构有限元分析模型,对其进行自振特性分析,提取前100阶模态的自振频率、振型等模态信息,其中前100阶模态的自振频率分布如图4所示。从图4可见,结构相邻模态间频率相差不大,属于频率分布密集型结构,因此,其模态响应耦合效应不能忽略。
按照文献[14]选取主要参振模态的方法,从自振特性分析提取的前100阶模态中选取对结构响应贡献较大的第1,2,4,3,6等共17阶(按照贡献程度排序)作为风振响应主要参振模态,利用风洞试验0°风向角时的风荷载测压值,基于随机振动理论,在频域内由背景响应、共振响应及其二者耦合项组合得到了脉动风荷载作用下结构位移极值响应[17],如图5所示。
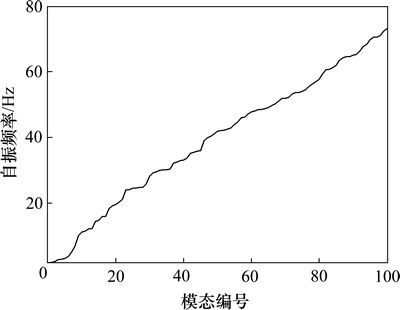
图4 结构前100阶自振频率分布
Fig. 4 Natural frequency distribution of the first 100 modes
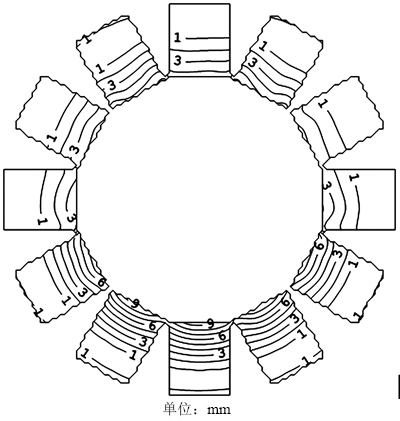
图5 脉动风荷载作用下结构位移极值响应
Fig. 5 Peak displacement response of structure induced by fluctuating winds
结合图3所示单元及风向角定度,由图5可以看出:屋盖结构挑棚悬挑端(内环位置)位移极值响应较大,尤其是沿着来流方向,处于尾流区域的6,7和8号单元挑棚悬挑端,其最大值达到9 mm,屋盖边缘区域响应值较小。据此,可以选取屋盖结构内环位置挑棚悬挑端位移响应较大的节点为响应控制节点。
5.2 多目标等效静力风荷载分析
根据脉动风荷载作用下结构风振响应分析结果,选取屋盖结构挑棚悬挑端(内环位置)响应较大的48个典型节点为目标响应控制节点(节点位置及编号如图3所示),采用本文所提精细化求解方法,计算其多目标等效静力风荷载。
根据所选48个典型节点响应求解结果,构造多目标等效静力风荷载的各基本分量Feq,b,i,Feq,r,i和Feq,b,r,i (i=1, 2, …, 48),并按照2.4节中的方法对其进行归并精简,归并精简后剩余的背景分量为Feq,b,1,Feq,b,2,Feq,b,5和Feq,b,6等共18组;剩余的共振分量为Feq,r,1,Feq,r,2,Feq,r,5和Feq,r,6等共21组;剩余的耦合项分量为Feq,b,r,1,Feq,b,r,2,Feq,b,r,4和Feq,b,r,5等共23组。将上述基本分量代入式(35)和(2),并结合边界条件方程式(29)计算其组合系数,由此组合得到多目标等效静力风荷载,同时按照第3节中方法对其进行修正,最终得到精细化多目标等效静力风荷载求解结果,如图6所示。图7所示为该精细化多目标等效静力风荷载作用下结构静力响应与频域分析所得极值响应对比结果(选取结构内环位置响应较大的48个典型节点)。
从图6可以看出:所得精细化多目标等效静力风荷载无奇异值出现,数值均在0.5 kN/m2以内,且分布较均匀,方便结构设计时与自重、其他活载等进行荷载组合。由图7可以看出:该精细化多目标等效静力风荷载作用下结构静力响应与目标响应也总体上较吻合,虽有个别响应较小的节点出现偏差,但误差不大,满足工程精度要求。
为了比较,图8分别给出了未引入边界条件方程且未修正(以下简称为第1类)以及引入边界条件方程未修正(以下简称为第2类)多目标等效静力风荷载计算结果。图9所示为该2类多目标等效静力风荷载作用下结构静力响应与频域分析所得极值响应对比结果(选取结构内环位置响应较大的48个典型节点)。
图6 精细化分析得到的脉动风产生的多目标等效静力风荷载
Fig. 6 Multi-target equivalent static wind loads induced by fluctuating winds through refinement analysis
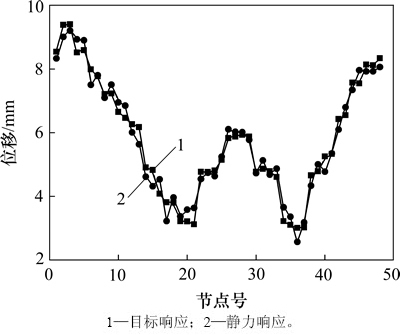
图7 精细化多目标等效静力风荷载下静力响应与目标响应对比
Fig. 7 Comparison between static response and target response for multi-target equivalent static wind loads through refinement analysis
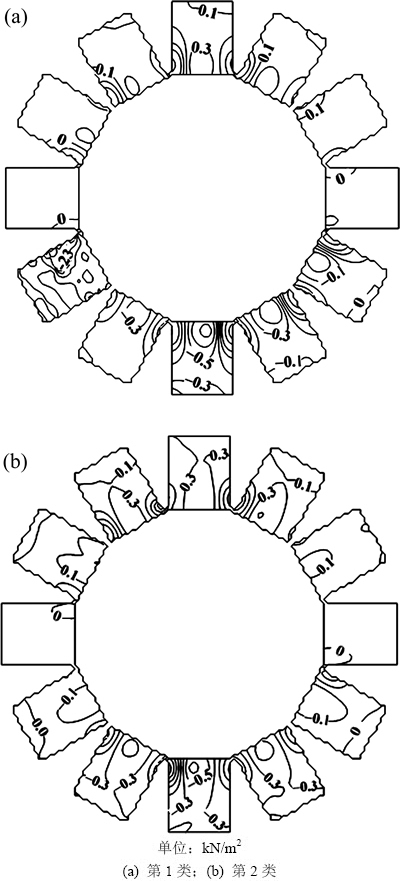
图8 脉动风产生的多目标等效静力风荷载
Fig. 8 Multi-target equivalent static wind loads induced by fluctuating winds
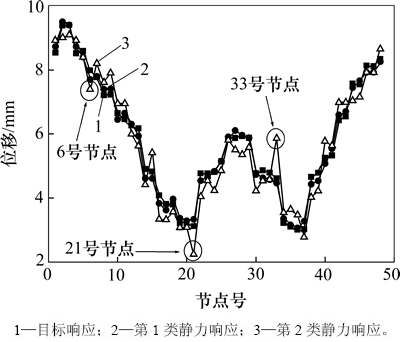
图9 多目标等效静力风荷载下静力响应与目标响应对比
Fig. 9 Comparison between static response and target response for multi-target equivalent static wind loads
从图9可以看出:第1类多目标等效静力风荷载作用下结构静力响应与目标响应较吻合,但从图8(a)发现其分布并不合理,4号、10号单元上荷载几乎为0 kN/m2,9号单元上出现了奇异值,达到-23 kN/m2,无法与结构自重、其他活载等进行荷载组合;图8(b)中,引入边界条件方程后的第2类多目标等效静力风荷载没有出现奇异值,均在0.5 kN/m2以内,且分布比较均匀。但从图9可以发现:该等效静力风荷载作用下结构静力响应与目标响应在部分节点上出现较大偏差,如第6,21和33号等节点,第1类静力响应和第2类静力响应的计算结果与目标响应间的计算结果相对误差均超过6%。可见:此2类多目标等效静力风荷载均没有图6、图7所示的精细化方法求解结果较理想。
6 结论
1) 根据大跨屋盖结构风振响应特性,基于LRC法基本原理推导得到多目标等效静力风荷载基本分量,与风振响应分析结果完全对应,且物理意义明确,据此构造的多目标等效静力风荷载能够再现风振响应特性。
2) 根据多目标等效静力风荷载基本分量作用下结构静力响应分布相似程度,对其进行归并精简,能够保证所选基本分量更加高效,实现了用较少的基本分量完成尽可能多的目标响应等效。
3) 引入求解多目标等效静力风荷载的边界条件方程与修正方程,可以较好地解决基于数值方法求解多目标等效静力风荷载所造成的计算结果离散性大、不便于工程应用、精度低的问题。
4) 采用本文方法对国家网球中心“莲花”球场屋盖结构多目标等效静力风荷载进行分析,所得多目标等效静力风荷载分布合理,且该多目标等效静力风荷载作用下结构静力响应与频域分析所得极值响应吻合较好,满足工程应用要求。
参考文献:
[1] DAVENPORT A G. Gust loading factors[J]. Journal of Structural Division, 1967, 93(3): 11-34.
[2] SOLARI G. Gust buffeting Ⅱ: dynamic along wind response[J]. Journal of Structural Engineering, 1993, 119(2): 383-398.
[3] 张相庭. 结构风工程理论·规范·实践[M]. 北京: 建筑工业出版社, 2006: 99-118.
ZHANG Xiangting. Wind engineering theory, code and practice[M]. Beijing: China Architecture and Building Press, 2006: 99-118.
[4] KASPERSKI M, NIEMANN H J. The LRC method: a general method of estimation unfavorable wind load distributions for linear and non-linear structures[J]. Journal of wind Engineering and Industrial Aerodynamics, 1992, 41(44): 1753-1763.
[5] 李毅, 李秋胜. 基于风振响应的高层建筑等效静力风荷载优化设计研究[J]. 湖南大学学报(自然科学版), 2013, 40(4): 26-31.
LI Yi, LI Qiusheng. Wind-induced response based equivalent static wind load optimum design for tall building[J]. Journal of Hunan University (Natural Science), 2013, 40(4): 26-31.
[6] HOLMES J D. Effective static load distributions in wind engineering[J]. Journal of wind Engineering and Industrial Aerodynamics, 2002, 90(2): 91-109.
[7] 邹云峰, 李寿英, 牛华伟, 等. 双曲冷塔等效静力风荷载规范适应性研究[J]. 振动与冲击, 2013, 32(11): 100-105.
ZOU Yunfeng, LI Shouying, NIU Huawei, et al. Adaptability study on a China’s code for equivalent static wind load of hyperbolic cooling towers[J]. Journal of Vibration and Shock, 2013, 32(11): 100-105.
[8] KATSUMURA A, TAMURA Y, NAKAMURA O. Universal wind load distribution simultaneously reproducing largest load effects in all subject members on large-span cantilevered roof[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(9): 1145-1165.
[9] TAMURA Y, KIKUCHI H, HIBI K. Actual extreme pressure distributions and LRC formula[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(12): 1959-1971.
[10] 段旻, 倪振华, 谢壮宁. 大跨屋盖的包络等效静风荷载[J]. 振动与冲击, 2008, 27(9): 6-10.
DUAN Min, NI Zhenhua, XIE Zhuangning. Envelope equivalent static wind load distribution on large roofs[J]. Journal of Vibration and Shock, 2008, 27(9): 6-10.
[11] 杨庆山, 陈波, 武岳. 基于Ritz-POD的大跨屋盖结构风振响应分析和风效应静力等效方法[J]. 建筑结构学报, 2011, 32(12): 127-136.
YANG Qingshan, CHEN Bo, WU Yue. Wind-induced response and equivalent static wind loads of long span roofs based on Ritz-POD method[J]. Journal of Building Structures, 2011, 32(12): 127-136.
[12] ZHOU Xuanyi, GU Ming. An approximation method for computing the dynamic responses and equivalent static wind loads of large-span structures[J]. International Journal of Structural Stability and Dynamics, 2010, 10(5): 1141-1165.
[13] 罗楠, 廖海黎, 李明水. 大跨屋盖时域多目标等效静力风荷载计算方法[J]. 工程力学, 2013, 30(4): 316-321.
LUO Nan, LIAO Haili, LI Mingshui. Universal equivalent static wind loads for long-span roofs in time domain[J]. Engineering Mechanics, 2013, 30(4): 316-321.
[14] 李玉学, 杨庆山, 田玉基. 大跨屋盖结构风致动力响应高阶主导模态的识别[J]. 北京交通大学学报, 2010, 34(1): 89-94.
LI Yuxue, YANG Qingshan, TIAN Yuji. Identification of high frequency modes with significant contributions to wind-induced vibration of large-span roofs[J]. Journal of Beijing Jiaotong University, 2010, 34(1): 89-94.
[15] CLOUGH R W, PENZIEN J. Dynamics of structures[M]. Berkeley: Computer & Structures Inc, 2003: 539-541.
[16] DAVENPORT A G. How can we simplify and generalize wind loads[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 54/55: 657-669.
[17] 李玉学, 杨庆山, 田玉基, 等. 大跨屋盖结构风致背景响应和共振响应实用组合方法[J]. 振动与冲击, 2014, 33(19): 199-206.
LI Yuxue, YANG Qingshan, TIAN Yuji, et al. Practical combination method for wind-induced background response and resonant response of large-span roofs[J]. Journal of Vibration and Shock, 2014, 33(19): 199-206.
(编辑 陈灿华)
收稿日期:2015-07-18;修回日期:2015-09-22
基金项目(Foundation item):国家自然科学基金资助项目(51278314,51378061);河北省自然科学基金资助项目(E2012210002);河北省大型基础设施防灾减灾创新中心基金资助项目(Z994001);河北省高等学校科学技术研究优秀青年基金资助项目(YQ2013028);石家庄铁道大学优秀青年基金资助项目(Z9901503);上海市工程结构安全重点实验室基金资助项目(2015-KF09) (Projects(51278314, 51378061) supported by the National Natural Science Foundation of China; Project(E2012210002) supported by the Natural Science Foundation of Hebei Province; Project(Z994001) supported by the Research Foundation of Hebei Collaborative Innovation Center of Large Infrastructure Disaster Prevention; Project(YQ2013028) supported by the Research Foundation of Hebei Higher Education Institutions; Project(Z9901503) supported by the Research Foundation of Shijiazhuang Tiedao University; Project(2015-KF09) supported by the Research Foundation of Shanghai Key Laboratory of Engineering Structure Safety)
通信作者:李玉学,博士,副教授,从事大跨空间结构抗风研究;E-mail: liyuxue2000@163.com