中外混凝土规范裂缝控制标准的可靠度分析与比较

李扬，侯建国

(武汉大学 土木建筑工程学院，湖北 武汉，430072)

摘要：通过引入模糊示性函数的蒙特卡洛方法，对我国规范GB 50010—2002，GB 50010—2010以及欧洲规范EN 1992-1-1:2004和美国规范ACI 318—08裂缝控制标准基于耐久性要求的模糊可靠指标β_w进行计算分析和比较。分析结果表明：与GB 50010—2002 规范中的β_w 相比，GB 50010—2010规范中的β_w在潮湿大气环境下和氯离子侵蚀环境下均下降50%；与EN 1992-1-1:2004规范中的β_w相比，GB 50010—2010规范中的β_w在潮湿大气环境下和氯离子侵蚀环境下分别偏高305%和146%；与ACI 318—08规范中的β_w在潮湿大气环境下和氯离子侵蚀环境下相比，GB 50010—2010 规范中的β_w分别偏高462%和55%。从合理的安全度设置水平角度出发，建议针对GB 50010—2010规范，可将普通潮湿大气环境下的裂缝宽度限值从当前的0.2 mm提高至0.25 mm，或将裂缝宽度计算保证率从当前的95%降为90%。

关键词：混凝土裂缝控制；可靠度指标；安全度设置水平；保证率；裂缝宽度限值

中图分类号：TU375.1                 文献标志码：A         文章编号：1672-7207(2013)09-3786-07

Comparison analysis of reliability of crack control criteria for Chinese and foreign concrete design specifications

LI Yang, HOU Jianguo

(School of Civil Engineering, Wuhan University, Wuhan 430072, China)

Abstract: The fuzzy reliability indexes based on durability of concrete crack control criteria for both damp air environment and chloride environment given by GB 50010—2002, GB 50010—2010, EN 1992-1-1:2004 and ACI 318—08 were calculated and compared by applying the Monte Carlo method with fuzzy indicator function. The calculation results indicate that for damp air environment and chloride environment, the reliability indexes of GB 50010—2010 are 50% lower than that of GB 50010—2002; For damp air environment and chloride environment, the reliability indexes of GB 50010—2010 are respectively 305% and 146% higher than that of EN 1992-1-1:2004, as well as 462% and 55% higher than that of ACI 318—08. Considering the rational safety level, the crack width limit should be increased from present 0.2 mm to 0.25 mm or the crack width calculation guarantee rate should be lowered from present 95% to 90% for crack control criteria given by GB 50010—2010 for damp air environment.

Key words: concrete member crack width control; reliability index; safety level; guarantee rate; crack width limit value

当前国内外关于混凝土结构件的裂缝开展机理及裂缝宽度计算理论有很多，导致各国混凝土结构设计规范的裂缝控制设计方法差别较大。李春秋等^[1-2]从短期裂缝宽度计算公式的保证率、荷载效应组合、是否考虑长期作用效应的影响及裂缝宽度限值等多个角度出发，通过定性角度探求国内外相关规范裂缝控制标准安全度设置水平的差异。李志华等^[3-4]则在此基础上以试验数据为样本，将实测值与按照多个国家混凝土规范的裂缝宽度计算公式得到的计算值进行比较，由此反映不同规范裂缝控制标准安全度设置水平的差异。上述研究主要是比较裂缝宽度计算值，虽然在一定程度上反映出不同规范裂缝控制标准安全度设置水平的差异，但难以反映出究竟哪个规范的裂缝控制标准的安全度设置水平更为合理。使得目前有部分研究者给出的我国规范混凝土构件裂缝控制标准应借鉴国外规范混凝土构件裂缝控制标准的建议，缺乏合理而有效的依据。此外，新近颁布的GB 50010—2010(《混凝土结构设计规范》)^[5]针对混凝土构件裂缝控制标准的规定进行了较大幅度的调整^[6]，其安全度设置水平在现有国内外混凝土规范裂缝控制标准中究竟处于什么样的地位，是否有必要对我国现行规范裂缝控制标准规定进行进一步的修订以及如何修订，针对上述问题，本文作者通过引入模糊示性函数的蒙特卡洛方法，开展了基于耐久性要求的混凝土构件裂缝控制模糊可靠度指标计算，对我国原混凝土规范GB 50010—2002、现行规范GB 50010—2010、美国规范ACI318—08^[7]以及欧洲规范EN 1992-1-1: 2004^[8]裂缝控制标准的安全度设置水平进行定量分析和比较，并在此基础上对我国现行混凝土规范裂缝控制标准提出修订建议，以便为我国混凝土规范的修订以及相关领域人员从事研究提供参考。

1  国内外混凝土规范裂缝控制标准简介

1.1  GB 50010—2010规范以及GB 50010—2002规范

GB 50010—2010规范规定，矩形、T形、倒T形和Ⅰ形截面的钢筋混凝土受拉、受弯和偏心受压构件，按荷载准永久组合并考虑长期作用影响的最大裂缝宽度可按下式计算：

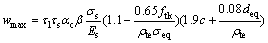  (1)

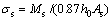               (2)

式中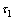：为长期裂缝宽度扩大系数；α_c为裂缝间混凝土自身伸长对裂缝宽度的影响系数；τ_s为短期裂缝扩大系数；σ_s为按荷载准永久组合计算的构件纵向受拉钢筋应力，N/mm²；E_s为钢筋弹性模量，N/mm²；β为反映受力类型差异的系数；f_tk为混凝土轴心抗拉强度标准值，N/mm²；c为最外层纵向受拉钢筋外边缘至受拉区底边的距离，mm，当c＜20 mm时，取c=20 mm；当c＞65 mm时，取c=65 mm；ρ_te为按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率，ρ_te=A_s/A_te，当ρ_te<0.01时，取ρ_te=0.01；A_s为受拉区纵向钢筋截面面积，mm²；d_eq为受拉区纵向钢筋的等效直径，mm；M_s为准永久荷载组合引起的构件截面弯矩，N·mm；h₀为混凝土构件截面有效高度，mm。关于上述各变量的取值原则和范围见GB 50010—2010。

GB 50010—2010规范裂缝计算公式与GB 50010—2002规范裂缝宽度计算公式基本相近，其主要的差别在于GB 50010—2002规范采用标准组合计算裂缝宽度。

1.2  ACI 318—08规范

ACI 318—08中的混凝土构件裂缝控制对象为标准荷载效应组合引起的混凝土构件受拉区表面短期裂缝宽度最大值。该规范通过限制受拉钢筋间距s来间接实现对裂缝宽度的限制。

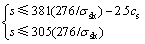          (3)

式中：σ_sk为受拉钢筋应力，N/mm²，可利用标准荷载组合根据弹性理论进行计算，见式(4)，或取受拉钢筋屈服强度的60%；s为相邻受拉钢筋间距，mm；c_s为受拉钢筋重心到受拉构件底面的距离，mm。关于上述各变量的取值原则和范围见ACI 318—08。

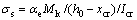           (4)

式中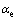：为钢筋与混凝土的弹性模量比；M_k为标准荷载引起的构件截面弯矩，N·mm；x_cr为开裂截面处混凝土受压区的高度，mm；I_cr为开裂截面的惯性矩，mm⁴。

式(3)主要参考了Frosch提出的裂缝宽度w_c计算公式并经线性化处理后得到^[8]。Frosch^[9]公式如下：

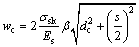            (5)

式中：d_c为从受拉区底面至最靠近该面的受拉钢筋截面形心的距离，mm；β为受拉区表面至中性轴的距离与钢筋重心至中性轴的距离之比。上述各变量的取值原则和范围见文献[9]。

1.3  EN 1992-1-1:2004规范

EN 1992-1-1:2004规范规定普通钢筋混凝土构件按准永久荷载效应组合并考虑长期作用影响计算裂缝宽度最大值w_k：

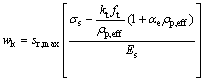        (6)

式中：s_{r, max}为裂缝间距，mm；ρ_{p, eff}为有效配筋率；k_t为与荷载作用时间长短相关的系数。关于上述各变量的取值原则和范围见EN 1992-1-1:2004。

2  混凝土构件裂缝控制标准模糊可靠指标的计算

考虑到我国规范给出的混凝土构件裂缝宽度计算公式较全面地反映了各个变量对裂缝宽度的影响^[3]，且参考文献[11]可以得到关于该公式的计算模式不定性系数的统计研究资料。因而本文将构件在荷载作用下考虑长期作用效应后的最大裂缝宽度随机值计算公式按下式取用：

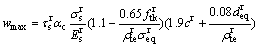   (7)

式(7)中，除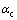外，其他变量均为随机变量，各变量意义见式(1)，这里对每个变量加上角标“r”以将其与式(1)中对应的各变量相区别。关于各变量的分布类型以及相应的变量均值和标准差取值均统一依据文献[11]给出。式(7)中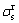为考虑长期作用对裂缝宽度的扩大效应后的等效受拉钢筋应力随机值(N/mm²)，本文将永久荷载效应以及可变荷载的准永久值效应视为长期作用，进而按下式计算：

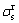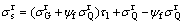        (8)

式中：τ_l为长期作用引起的裂缝宽度扩大系数，本文中近似取1.5；ψ_f为准永久值系数，近似按照GB 50009—2001规范取用；和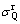分别为由于恒荷载以及活荷载引起的受拉钢筋应力随机值(N/mm²)。

国内外混凝土规范裂缝宽度计算公式中关于受拉钢筋应力的计算方法也存在差异，见式(2)与式(4)。将大量混凝土试件条件参数代入式(2)与式(4)发现两者的计算结果偏差整体不大。本文通过分别选用式(2)和式(4)计算受拉钢筋应力随机值，并在此基础上计算裂缝控制标准可靠指标，发现基于两式得到的裂缝控制标准可靠指标相差不大。为求统一，本文选用式(4)计算受拉钢筋应力随机值。

在计算式(7)中短期裂缝宽度扩大系数随机数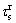时，需模拟生成单根构件上裂缝的总条数n，进而在n条裂缝宽度中模拟构件上产生的最大裂缝宽度，即依据τ_s的统计分布规律生成n个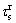，选择其中的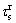最大值代入式(7)参与计算。裂缝条数n的计算见式(9)^[6]。τ_s的统计分布规律见文献[2]。

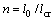                (9)

式中：l₀为构件出现正截面裂缝区段的长度(m)，它与正截面抗裂力有关，对拉杆可取全长，对钢筋混凝土梁式构件可近似取跨度的1/3；l_cr为平均裂缝间距(m)，理论上应为随作用效应增大而减小的变数，并趋向于某一稳定数值，本文近似按照GB 50010—2010规范的有关规定计算。

考虑到构件中混凝土裂缝宽度对构件耐久性影响的模糊性，本文采用引入模糊示性函数的蒙特卡洛法，在荷载作用下出现由于混凝土裂缝引起的构件耐久性失效的概率P_D，为

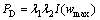            (10)

式中：λ₁为反映裂缝方向的综合影响系数；λ₂为裂缝密度影响系数；参考文献[12]，取λ₁=0.4；λ₂=1.0，I(w_max)为裂缝引起耐久性失效的模糊示性函数，可按采用升半型隶属函数描述^[6]：

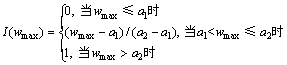 (11)

[a₁, a₂]为裂缝引起混凝土耐久性失效的模糊失效域(mm)。近年来，国内外基于试验研究以及理论推导得到了大量有关混凝土裂缝宽度对耐久性影响的研究成果。研究结果表明：虽然裂缝宽度不是影响混凝土耐久性的首要因素，但随着裂缝宽度的增大，有害物质通过裂缝更容易进入混凝土从而最终加快钢筋锈 蚀^[13-16]。考虑到不同试验研究所针对的混凝土试件形状以及试件中裂缝宽度取值位置的差异，本文依据应变梯度理论^[9]，将试验对象裂缝宽度统一近似换算为混凝土构件侧面受拉钢筋高度位置处的裂缝宽度。文献[13-14]基于水分以及氯离子在开裂混凝土中的扩散和渗透试验发现：当裂缝宽度在0.15 mm以内时，裂缝宽度的增大引起氯离子扩散和渗透性的增加并不显著。文献[15-16]则基于氯离子在开裂混凝土中的扩散试验指出：裂缝宽度在0.1~0.5 mm范围内变化时，相应的氯离子在混凝土中的扩散速度将大幅度提高。同时，文献[12]针对混凝土裂缝宽度对既有混凝土构件耐久性的影响情况指出：当裂缝宽度达到0.4 mm时，可以认为构件耐久性失效。考虑到通常氯离子侵蚀环境较潮湿大气环境对构件的耐久性具有更为不利的影响。本文在上述研究成果基础上，对[a₁, a₂]进行如下设定：针对潮湿大气环境条件，取a₁=0.15 mm，a₂=0.5 mm；针对氯离子侵蚀环境条件，取a₁=0.15 mm，a₂=0.4 mm。

将已知的构件截面参数条件以及可变荷载效应与永久荷载效应的比值代入各国规范裂缝宽度计算公式，依据裂缝宽度限值规定，反求出符合裂缝控制标准的最大荷载标准值(或准永久值)。利用已知的构件参数以及所求出的荷载参数，依据蒙特卡洛法经过m次独立抽样并联合式(7)和式(8)计算生成m个最大裂缝宽度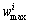，进而利用式(9)和式(10)生成m个失效概率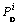，则总的裂缝引起构件耐久性失效的概率P_f即为所有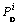的平均值。

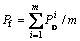             (12)

从而求得裂缝不引起构件耐久性失效的可靠指标为

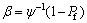             (13)

式中：为标准正态分布函数的反函数。

3  算例分析

3.1  计算条件

本文选取12根矩形混凝土构件作为研究对象，构件截面尺寸参数基本涵盖了实际工程中常用构件截面参数的范围。见表1。本文仅比较构件在纯受弯状态下的裂缝控制标准可靠指标。为简明起见，分析中选用了永久荷载＋办公楼可变荷载、永久荷载＋住宅可变荷载组合以及永久荷载+商店可变荷载组合。可变荷载与永久荷载的荷载效应比值取为0.10，0.25，0.50，1.00和2.00。

本文以普通潮湿大气环境条件以及氯离子侵蚀环境条件(主要指沿海区域环境)下中美欧混凝土规范裂缝宽度的限值为依据，对相应规范裂缝控制标准的可靠度指标进行计算。依据GB 50010—2002以及GB 50010—2010规范规定，针对潮湿大气环境以及氯离子侵蚀环境，均取裂缝宽度限值w_lim=0.2 mm；依据EN1992-1-1:2004规范规定，针对潮湿大气环境取w_lim=0.4 mm；针对氯离子侵蚀环境取w_lim=0.3 mm。由于美国规范ACI 318—08规定针对室内以及室外环境条件，均通过将混凝土受拉底面的最大裂缝宽度控制在0.4~0.55 mm以内来进行受拉钢筋间距的限制，故针对潮湿环境下无需给出裂缝宽度限值，直接按照式(5)进行验算。但该规范同时指出针对腐蚀环境较严重的情况下需采取专门的调查研究和预防措施限裂。依据美国ACI 224委员会的建议^[8]，针对氯离子侵蚀环境取混凝土构件受拉表面裂缝宽度限值w_lim= 0.15 mm，此时须依据Frosch公式(见式(5))进行裂缝宽度验算。

3.2  计算结果分析

结合上述计算条件，给出对应不同规范裂缝控制标准得到的单根构件裂缝控制标准可靠指标β_w计算结果，见图1。图1中每个可靠指标β_w为对应该构件在3种荷载效应组合以及5种荷载效应比值下的可靠指标β_w平均值。同时给出对应不同规范裂缝控制标准的可靠指标β_w与荷载效应比值ρ的关系图，见图2。

表1  用于裂缝控制可靠度分析的构件参数条件

Table 1  Concrete member parameters for crack control reliability analysis

图1  β_w与不同构件截面尺寸的关系

Fig.1  Relationship between β_w and concrete member parameters

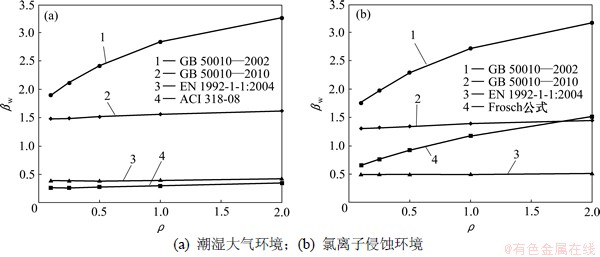
图2  β_w 与荷载效应比ρ的关系

Fig.2  Relationship between β_w and ρ

其中每种规范对应的β_w结果为本文所采用的12根构件在3种荷载作用效应组合下的β_w平均值。

结合图1可知：针对不同截面尺寸构件，除采用GB 50010—2002规范以及Frosch公式限裂外，采用其他规范裂缝控制标准限裂得到的可靠指标β_w变化幅度基本在0~0.5之间，表明可靠指标β_w受构件截面参数条件的变化影响相对并不敏感。结合图1和图2可知：GB 50010—2010规范、EN 1992-1-1:2004规范以及ACI 318—08规范对应的裂缝控制标准可靠指标β_w受荷载效应比ρ的影响相对较小。GB 50010—2002规范以及Frosch公式对应的可靠指标β_w随着ρ的增大而显著增大，当ρ从0.1变化至2.0时，相应的可靠指标β_w增幅在1.0以上。在不同构件截面参数以及荷载效应比条件下，裂缝控制标准的安全度设置水平应以保持相对平稳为宜，由此反映出GB 50010—2010规范、EN 1992-1-1:2004规范以及ACI 318—08规范的裂缝控制标准的安全度设置水平较合理。

结合图1和图2可知：GB 50010—2010规范中的可靠指标β_w相对于GB 50010—2002规范中的可靠指标β_w有所下降，在潮湿大气环境下以及氯离子侵蚀环境下均下降了50%，这主要是由于GB 50010—2010规范采用了准永久组合计算裂缝宽度，从而适当放宽了裂缝控制标准的安全度设置水平。然而，与EN 1992-1-1:2004规范以及ACI 318—08规范相比，GB 50010—2010规范中的可靠指标β_w仍旧偏大，在潮湿大气环境下比EN 1992-1-1:2004规范和ACI 318—08规范中的可靠指标β_w分别高305%和462%，在氯离子侵蚀环境下比EN 1992-1-1:2004规范和ACI 318—08规范中的可靠指标β_w分别高146%和55%。

GB 50153—2008(《工程结构可靠性设计统一标准》)规定：结构构件在正常使用极限状态下的目标可靠指标，根据其可逆程度宜取0~1.5。从耐久性设计目标可靠指标的取值出发，有研究指出混凝土耐久性失效的概率限值宜为7%~10%，即目标可靠指标宜达到1.3~1.5^[17]。因而，与其他规范相比，我国现行GB 50010—2010规范裂缝控制标准的安全度设置水平整体是比较合理的，只是针对潮湿大气环境下，裂缝控制标准安全度设置水平仍略偏高，可适当降低。

考虑到在通常情况下，构件是由承载能力极限状态控制设计的，因此，对实际构件而言，通常裂缝控制的可靠指标要高于本文的计算结果，即本文的计算结果是构件裂缝控制标准可靠指标的“底线”。

4  针对GB 50010—2010规范的修订建议

通常对于裂缝宽度控制标准安全度设置水平的调整方法，包括改变裂缝宽度限值w_lim，改变裂缝宽度计算保证率p等^[1-2]。图3和图4所示为GB 50010—2010规范裂缝控制标准可靠指标β_w随w_lim和p的变化情况。其中每个可靠指标β_w为本文所采用的12根构件在3种荷载作用效应组合及5种荷载效应比条件下的可靠指标β_w平均值。在考察可靠指标β_w与计算保证率p的关系时，取w_lim=0.2 mm；在考察可靠指标β_w与裂缝宽度限值w_lim的关系时，取p=95%。p主要与计算公式中短期裂缝宽度扩大系数τ_s有关^[2]。两者的对应关系为

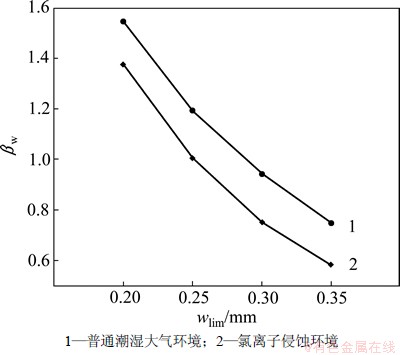
图3  β_w与w_lim的关系

Fig.3  Relationship between β_w and w_lim

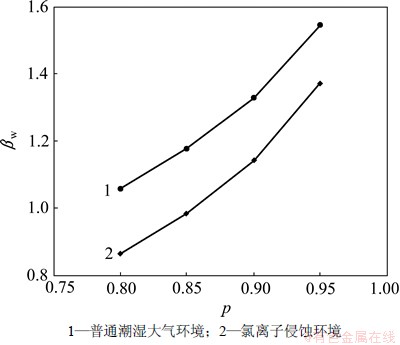
图4  β_w与p的关系

Fig.4  Relationship between β_w and p

            (14)

结合图3可知：针对潮湿大气环境与氯离子侵蚀环境，w_lim从0.2 mm提高到0.35 mm时相应的β_w降低了0.8左右；p从95%降低到80%时相应的β_w平均降低了0.5左右。结合图4可知：潮湿大气环境下对应p为90%时的β_w与氯离子环境下p为95%时的β_w基本相当。考虑到与氯离子侵蚀环境相比，针对潮湿大气环境下的裂缝控制标准目标可靠指标没有必要过高，使2种环境下的裂缝控制标准目标可靠指标一致或潮湿大气环境下的裂缝控制标准目标可靠指标略偏低一点均是可行的。基于此本文建议针对GB 50010—2010规范，可将潮湿大气环境下的裂缝宽度限值由0.2 mm提高为0.25 mm，或将裂缝宽度计算保证率由95%降为90%，即短期裂缝扩大系数τ_s降为1.5。经修订后的潮湿大气环境下β_w约为1.25。

5  结论

(1) 在不同构件截面参数条件以及荷载效应比条件下，应以保持裂缝控制标准可靠度指标相对平稳为宜，由此角度出发判断GB 50010—2010规范、EN 1992-1-1:2004规范以及ACI 318—08规范的裂缝控制标准的安全度设置水平相对较为合理。

(2) GB 50010—2010规范中的β_w相对于GB 50010—2002规范中的β_w均有所下降，在潮湿大气环境下及氯离子侵蚀环境下均下降了50%；与EN 1992-1-1:2004 规范中的β_w相比，GB 50010—2010规范中的β_w在潮湿大气环境下以及氯离子侵蚀环境下分别偏高305%和146%；与ACI 318—08规范中的β_w相比，GB 50010—2010 规范中的β_w在潮湿大气环境下以及氯离子侵蚀环境下分别偏高462%和55%。

(3) 本文建议针对GB 50010—2010规范，可将普通潮湿大气环境下的裂缝宽度限值指标从当前的0.2 mm提高至0.25 mm，或将裂缝宽度计算保证率从当前的95%降为90%，即将短期裂缝扩大系数τ_s从1.66降为1.50。经修订后的潮湿大气环境下β_w约为1.25。

参考文献：

[1] 李春秋, 陈肇元. 荷载作用下混凝土构件裂缝控制的若干问题[J]. 建筑结构, 2007, 37(1): 114-119.

LI Chunqiu, CHEN Zhaoyuan. Discussion on load-induced crack control for reinforced concrete members[J]. Building Structure, 2007, 37(1): 114-119.

[2] 李扬, 侯建国. 国内外混凝土构件裂缝控制安全度设置水平比较[J]. 建筑结构, 2011, 41(2): 124-127.

LI Yang, HOU Jianguo. Comparison of safety level of Chinese and foreign crack control of concrete members[J]. Building Structure, 2011, 41(2): 124-127.

[3] 李志华, 苏小卒, 赵勇, 等. 荷载作用下钢筋混凝土梁的裂缝控制规范比较[J]. 武汉理工大学学报, 2010, 32(13): 67-71.

LI Zhihua, SU Xiaozu, ZHAO Yong, et al. Comparative study on the design provisions for control of load-induced cracks in reinforced concrete members[J]. Journal of Wuhan University of Technology, 2010, 32(13): 67-71.

[4] 陈飞, 赵勇, 周建民. 美国规范ACI 318 的裂缝控制方法评析[J]. 建筑科学, 2009, 25(7): 93, 102-105.

CHEN Fei, ZHAO Yong, ZHOU Jianmin. Review of crack control methods in ACI 318 code[J]. Building Science, 2009, 25(7): 93, 102-105.

[5] GB 50010—2010, 混凝土结构设计规范[S].

GB 50010—2010, Code for design of concrete structures[S].

[6] 李扬, 侯建国. 混凝土构件裂缝控制模糊可靠度计算方法[J]. 武汉理工大学学报, 2012, 34(3): 80-85.

LI Yang, HOU Jianguo. Calculation method of fuzzy reliability level for crack control of concrete members[J]. Journal of Wuhan University of Technology, 2012, 34(3): 80-85.

[7] ACI 318—08, Building code requirements for structural concrete and commentary[S].

[8] ACI 224R—01, Control of Cracking in Concrete Structures[S].

[9] Frosch R J. Another look at cracking and crack control in reinforced concrete [J]. ACI Structure Journal, 1999，96(3): 437-442.

[10] EN 1992-1-1:2004, Design of concrete structures, Part 1: General rules and rules for building [S].

[11] 史志华, 胡德炘, 陈基发, 等. 钢筋混凝土结构构件正常使用极限状态可靠度的研究[J]. 建筑科学, 2000(6): 4-11.

SHI Zhihua, HU Dexin, CHEN Jifa, et al. Research on reliability of serviceability limit states for structural members of reinforced concrete[J]. Building Science, 2000(6): 4-11.

[12] 伍振志, 杨林德, 时蓓玲, 等. 裂缝对隧道管片结构耐久性影响及其模糊评价[J]. 地下空间与工程学报, 2007, 3(2): 224-228.

WU Zhenzhi, YANG Linde, SHI Beiling, et al. Study on the influence of crack on the durability of tunnel segments using fuzzy evaluation[J]. Chinese Journal of Underground Space and Engineering, 2007, 3(2): 224-228.

[13] Aldea C M, Shah S P, Karr A. Effect of cracking on water and chloride permeability of concrete[J]. Journal of Materials in Civil Engineering, 1999, 11(3): 181-187.

[14] Ismail M, Toumi A, R, et al. Effect of crack opening on the local diffusion of chloride in cracked mortar samples[J]. Cement and Concrete Research, 2008, 38(8/9): 1106-1111.

[15] Park S S, Kwon S J, Jung S H. Analysis technique for chloride penetration in cracked concrete using equivalent diffusion and permeation[J]. Cement and Concrete Research, 2011, 41(1): 9-19.

[16] 张君, 居贤春, 公成旭. 混凝土中的裂缝对氯盐侵蚀作用的影响[J]. 哈尔滨工程大学学报, 2010, 31(6): 720-724.

ZHANG Jun, JU Xianchun, GONG Chengxu. Effect of cracks in concrete on chloride penetration[J]. Journal of Harbin Engineering University, 2010, 31(6): 720-724.

[17] Kwon S J, Na U J, Park S S, et al. Service life prediction of concrete wharves with early-aged crack: Probabilistic approach for chloride diffusion[J]. Structural Safety, 2009, 31(1): 75-83.

(编辑  何运斌)

收稿日期：2012-08-02；修回日期：2012-10-25

基金项目：中央高校基本科研业务费专项资金资助项目(20102100101000092)

通信作者：侯建国(1955-)，男，湖北武汉人，教授，博士生导师，从事混凝土结构裂缝控制研究；电话：13807136598；E-mail: jghou@whu.edu.cn