Trans. Nonferrous Met. Soc. China 26(2016) 1729-1735
Primary-transient creep and anelastic backflow of pure copper deformed at low temperatures and ultra-low strain rates
Jun-jie SHEN1, Ken-ichi IKEDA2, Satoshi HATA2, Hideharu NAKASHIMA2
1. School of Mechanical Engineering, Tianjin University of Technology, Tianjin 300191, China;
2. Department of Electrical and Materials Science, Faculty of Engineering Sciences, Kyushu University, Kasuga, Fukuoka 816-8580, Japan
Received 19 May 2015; accepted 2 May 2016
Abstract: Creep and anelastic backflow behaviors of pure copper (4N Cu) with grain size dg=40 μm were investigated at low temperatures of T <0.3Tm (Tm is melting point) and ultra-low creep rates of 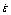 ≤1×10-10 s-1 by a high strain-resolution measurement (the helicoid spring specimen technique). Analysis of creep data was based on the scaling factors of creep curves instead of the conventional extrapolated steady-state creep rate. Power-law creep equation is suggested to be the best for describing the primary transient creep behavior, because the pre-parameter does not apparently change with elapsed time. The observed anelastic strains are 1/6 of the calculated elastic strains, and linear viscous behavior was identified from the logarithm plot of the anelastic strain rate versus anelastic strain (slope equals 1). Therefore, the creep anelasticity is suggested to be due to the unbowing of there-dimensional network of dislocations.
≤1×10-10 s-1 by a high strain-resolution measurement (the helicoid spring specimen technique). Analysis of creep data was based on the scaling factors of creep curves instead of the conventional extrapolated steady-state creep rate. Power-law creep equation is suggested to be the best for describing the primary transient creep behavior, because the pre-parameter does not apparently change with elapsed time. The observed anelastic strains are 1/6 of the calculated elastic strains, and linear viscous behavior was identified from the logarithm plot of the anelastic strain rate versus anelastic strain (slope equals 1). Therefore, the creep anelasticity is suggested to be due to the unbowing of there-dimensional network of dislocations.
Key words: pure copper; creep; dislocation; anelasticity; constitutive creep equation
1 Introduction
It has been known that creep deformation can occur at very low strain rates of 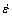 ≤1×10-10 s-1 [1-3]. Analysis of creep data is conducted usually based on the creep rate in the secondary creep stage. However, at
≤1×10-10 s-1 [1-3]. Analysis of creep data is conducted usually based on the creep rate in the secondary creep stage. However, at 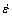 ≤1×10-10 s-1, identification of the secondary creep stage requires very long testing time, even longer than 40 years [1]. Such long testing time cannot be accepted for systematic study of creep deformation at
≤1×10-10 s-1, identification of the secondary creep stage requires very long testing time, even longer than 40 years [1]. Such long testing time cannot be accepted for systematic study of creep deformation at 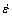 ≤1×10-10 s-1. Therefore, steady-state creep rates extrapolated by fitting primary transient creep curves were used to study long-term creep deformation [4-6]. To obtain analyzable primary transient creep data at
≤1×10-10 s-1. Therefore, steady-state creep rates extrapolated by fitting primary transient creep curves were used to study long-term creep deformation [4-6]. To obtain analyzable primary transient creep data at 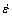 ≤1×10-10 s-1, a helicoid spring specimen technique has been employed [4-6] due to its higher strain resolution than that of conventional uniaxial tension creep tests, even reaching 1×10-9 [7].
≤1×10-10 s-1, a helicoid spring specimen technique has been employed [4-6] due to its higher strain resolution than that of conventional uniaxial tension creep tests, even reaching 1×10-9 [7].
However, it is not clear whether the creep data analysis based on extrapolating steady-state creep rates by fitting primary transient creep curves is the best approach, because the steady-state creep stage is often not reached [8]. Actually, the steady-state strain rate is considered to be identical to the creep rate derived (directly) at the end of the creep curves [5]. In addition, this approach hides an error of taking a steady-state creep rate instead of the minimum creep rate. The physical meanings of the steady-state creep rate and the minimum creep rate are completely different. The former, steady-state creep rate, is associated with a balance of work hardening and creep recovery under the condition of a stable microstructure, whereas the latter, the minimum creep rate, may be related with a balance point of work hardening and recovery caused by deterioration of microstructure.
Here, an alternative approach was shown to analyze creep data at ultra-low strain rate, 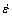 <1×10-10 s-1, using scaling factors of the creep curves. The scaling factors should determine shape of creep curves and are independent of the elapsed testing-time. The dependence of the scaling factors on stress and temperature is examined instead of examining the dependence of conventional steady-state creep rates on stress and temperature. We preformed helicoid spring creep tests on pure copper (99.99% Cu) at T<0.3Tm (Tm is the melting point) and ultra-low strain rate,
<1×10-10 s-1, using scaling factors of the creep curves. The scaling factors should determine shape of creep curves and are independent of the elapsed testing-time. The dependence of the scaling factors on stress and temperature is examined instead of examining the dependence of conventional steady-state creep rates on stress and temperature. We preformed helicoid spring creep tests on pure copper (99.99% Cu) at T<0.3Tm (Tm is the melting point) and ultra-low strain rate, 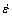 <1×10-10 s-1. Creep curves were analyzed by the use of transient constitutive creep equations to find possible scaling factors. Then, dependence of the scaling factors on stress, temperature and testing time was analyzed. The characteristics of an anelastic process at
<1×10-10 s-1. Creep curves were analyzed by the use of transient constitutive creep equations to find possible scaling factors. Then, dependence of the scaling factors on stress, temperature and testing time was analyzed. The characteristics of an anelastic process at 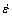 <1×10-10 s-1 were also firstly studied with regard to its magnitude and kinetics to better understand the creep behavior.
<1×10-10 s-1 were also firstly studied with regard to its magnitude and kinetics to better understand the creep behavior.
2 experimental
Creep tests were performed on wires of 99.99% Cu (4N) with a diameter of 1.6 mm supplied by Nilaco Corporation (Japan). The following equations [9,10] were used to calculate the mean surface shear stress, t, and the surface shear strain, g, assuming pure torsion of the helicoid spring specimen:
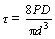 (1)
(1)
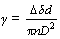 (2)
(2)
where P is the average load, D is the coil diameter (18.8 mm), d is the wire diameter (1.6 mm), n is the number of coils (5) measured and △δ is the displacement of the mean coil-pitch spacing. In this work, torsion is the dominant component of deformation because D is much greater than d (D/d >12) [11] and the value of d is between 2.5 and 4.0 mm [8]. Since the stress and strain in the helicoid spring have essentially shear components, they can be transformed to the equivalent tensile quantities using von Mises equations for tensile stress 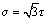 and tensile strain
and tensile strain  The minimum detectable value of strain for the helicoid spring creep test is evaluated from Eq. (2). For example, the minimum detectable strain for the present experiment is ε=4.2×10-8 under the following conditions: d =1.6 mm; D=18.8 mm; n=10; △δ is measured using a light-emitting diode with a resolution of 0.5 μm. Details of the test apparatus were reported elsewhere [12-14].
The minimum detectable value of strain for the helicoid spring creep test is evaluated from Eq. (2). For example, the minimum detectable strain for the present experiment is ε=4.2×10-8 under the following conditions: d =1.6 mm; D=18.8 mm; n=10; △δ is measured using a light-emitting diode with a resolution of 0.5 μm. Details of the test apparatus were reported elsewhere [12-14].
3 results and discussion
3.1 Creep curve description
The creep curves obtained at 298, 348 and 398 K are shown in Figs. 1(a)-(c), respectively. In all the creep curves, the creep rate which corresponds to the slope of the curves decreases with the increase of time. Figure 2 shows the strain rate on a logarithmic plot versus strain at 348 K and different stresses. Creep deformation of the pure copper consists of primary creep stages, in which the creep rate decreases with the increase of strain and no secondary (steady-state) creep stage is observed, in which the creep rate does not change with strain.
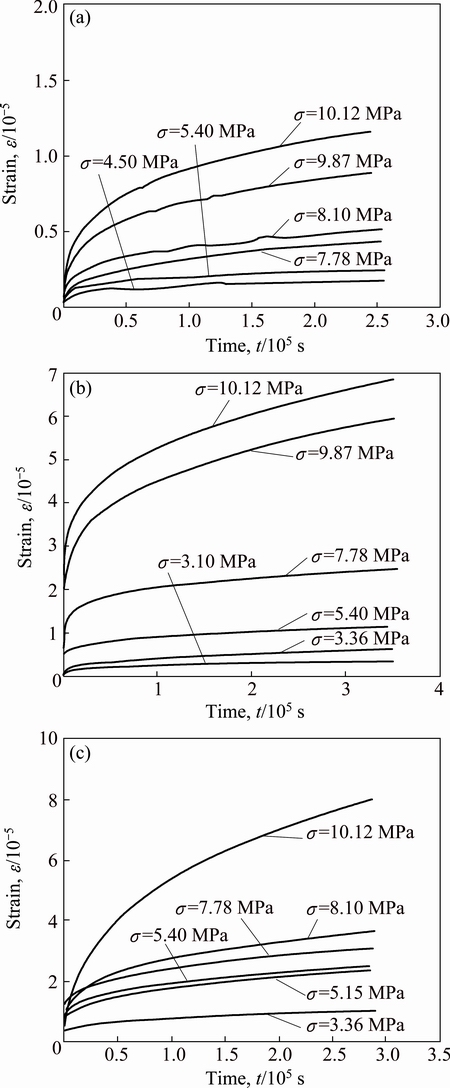
Fig. 1 Strain-time creep curves for Cu (4N) at 298 K (a), 348 K (b) and 398 K (c)
Therefore, constitutive creep equations expressing the primary stages should be used to analyze the experimental creep curves. We used the following constitutive creep equations that are widely accepted as basic equations [14,15].
Power law:
ε=ε0+atb (3)
Exponential law:
ε=ε0+a[1-exp(-bt)] (4)
Logarithmic law:
ε=ε0+aln(1+bt) (5)
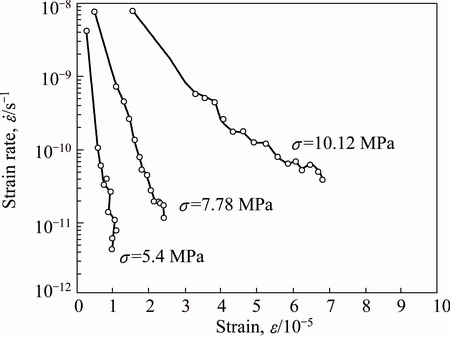
Fig. 2 Strain rate-strain creep curves at 348 K and different stresses
Blackburn’s law:
ε=ε0+ac[1-exp(-bt)]+c[1-exp(-dt)] (6)
where ε is the strain, ε0 is the instantaneous strain on application of dead weight, t is the elapsed time, and a, b, c and d are parameters characterizing the primary creep region. Here, we call a, b, c and d “scaling factors”.
Typical results of a regression analysis are shown in Fig. 3, for creep at 348 K and 7.78 MPa. The curves predicted from these equations are extrapolated to predict the creep course. The exponential-law equation does not reproduce the experimental data, whereas power-law equation, Blackburn’s equation and logarithmic-law equation all give a good representation of the experimental creep curve. The e0 and the parameters, a, b, c and d, obtained from these equations that best fit the experimental creep curve are used to analyze creep behavior.
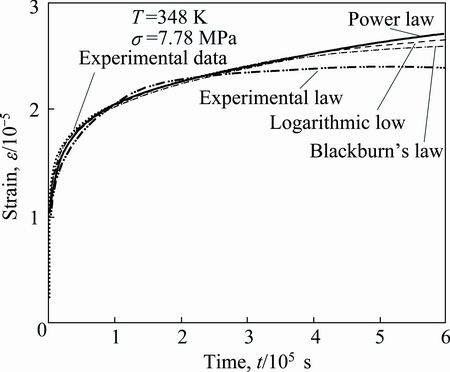
Fig. 3 Comparison of experimental data and predicted extrapolated curves of strain versus time at 348 K and 7.78 MPa
3.2 Instantaneous strain
On application of load, there is an instantaneous specimen strain. The instantaneous strains predicated from the power-law equation, Blackburn’s equation and the logarithmic-law equation are very close to each other, as illustrated in Fig. 4. This figure also shows that the square root of the instantaneous strain, ε01/2, is a linear function of the applied stress. This result is reasonable because the stress-strain curves of copper are approximately parabolic and the instantaneous strain on the application of a load corresponds to this relationship [16]. The extrapolated value of stress at ε01/2=0 may be regarded as the elastic limit σ0 [16] indicated by a arrow in Fig. 4. At 348 K, the value is about 2.5 MPa.
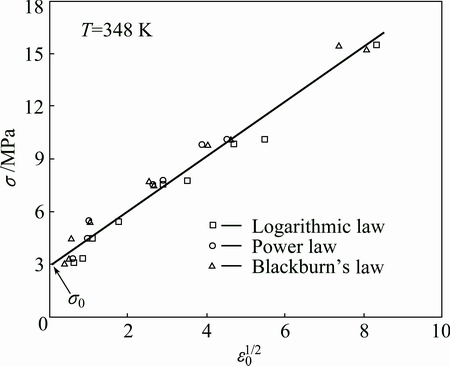
Fig. 4 Applied stress versus ε01/2 power of instantaneous strain predicted by different creep equations for pure copper at 348 K
3.3 Dependence of parameters on stress and temperature
In Figs. 5(a)-(c), the scaling factors, a, b, c and d, obtained from the creep constitutive equations: the power-law equation, Blackburn’s equation and the logarithmic-law equation, respectively, are plotted against applied stresses on a logarithm scale. The dependence of the values of a, b, c and d on stress is attempted to describe by the following power-law relationship:
a, b, c and d =σn (7)
where n is the stress exponent.
For fitting the creep data by the power-law equation in Fig. 5(a), parameter b (open circle), is b≈1/3 and independent of stress, whereas a (open square) shows the tendency of a=σ2. For the case of Blackburn’s law in Fig. 5(b), the parameters, b (blue) and d (green), are independent of stress, whereas a (red) and c (triangle) are dependent on stress as a, b ≈σ3, respectively. For the case of the logarithmic-law equation in Fig. 5(c), the parameter, b (open circle), is independent of stress, whereas a (open square) is dependent on stress as a≈σ3. Actually, parameters b and d should be considered to represent the average of small deviations from the power, double-exponential and logarithmic behaviors whereas terms a and c mainly decide the creep progression. The small deviations represent experimental inaccuracies, i.e., the instability of the experimental temperature.
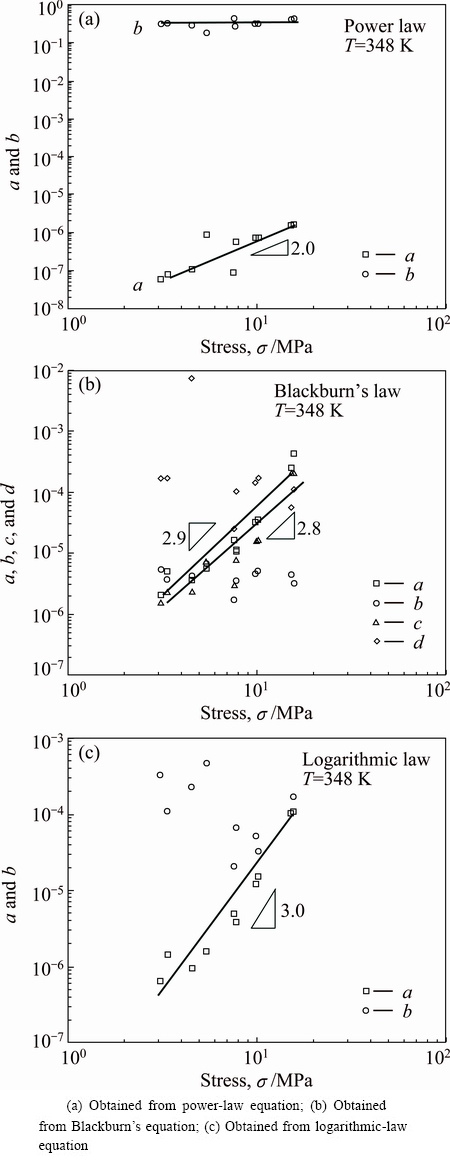
Fig. 5 Dependence of parameters a, b, c and d on stress at 348 K
The dependence of parameters a and c on temperature is attempted to describe by the Arrhenius equations:
 (8)
(8)
and
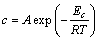 (9)
(9)
where A is a constant that depends on the materials and stress, R is the molar gas constant, T is the test temperature and Ea and Ec are the activation energies for creep. Figure 6 shows determined values of a and c in the power-law equation, Blackburn’s equation and logarithmic-law equation, on a logarithmic scale plotted against the reciprocal temperature, T -1, at applied stresses of 5.40, 7.78 and 10.12 MPa. The power-law equation in Fig. 6(a) shows Ea=(30±10) kJ/mol and the Blackburn’s equation in Fig. 6(b) shows Ea= (19±10) kJ/mol and Ec=(23±7) kJ/mol. The logarithmic- law equation in Fig. 6(c) shows Ea=(23±9) kJ/mol.

Fig. 6 Dependence of parameters a and c on reciprocal temperature at different stresses of 5.40, 7.78 and 10.12 MPa
To study the dependence of parameters a and c on the creep time (creep progress), the creep curves at 298 K, 4.4 MPa and different testing time, 3.4×105, 4.8×105, 8.0×105 and 12.0×105 s, are described by the power-law equation, Blackburn’s equation and the logarithmic-law equation. The results are summarized in Fig. 7. For the logarithmic-law equation and Blackburn’s equation, parameters a and c slightly decrease with elapsed time, whereas a values for the power-law equation do not apparently change with elapsed time. The result means that the scaling factor a for the power-law equation is independent of creep time. Therefore, the power-law equation may be best used to describe creep curves obtained by the helicoid spring creep tests, and the dependence of parameter a on stress and temperature should be used to study the transient creep behavior. Parameter a should reflect some characters of microstructure and not change with creep progress.
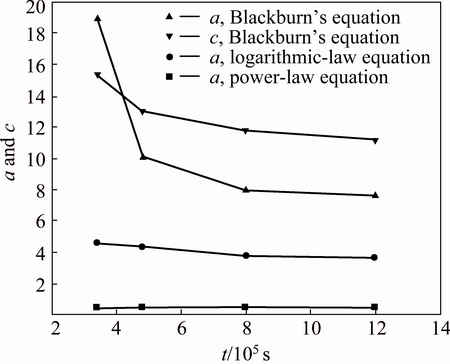
Fig. 7 Dependence of parameters a and c obtained from power-law, logarithmic-law and Blackburn’s equations, on creep time (creep progress)
3.4 Anelastic back-flow
A typical back-flow phenomenon observed for a large reduction in stress during the transient creep stage at 348 K is shown in Fig. 8, where the elastic strain has been removed. The inset shows a magnified view of the anelastic back-flow deformation. The absolute value of the anelastic strain rate gradually decreases with back-flow progress.
To examine the physical origin of the anelastic back-flow process, we characterized the magnitude and the kinetics of the process. We plot anelastic strain versus strain at 7.78 MPa (Fig. 9(a)) and 10.12 MPa (Fig. 9(b)) on a logarithm scale. The slopes of all curves are all equal to 1. This indicates that the kinetic of the anelastic back-flow process is linearly viscous. The viscous behavior of anelastic back-flow at very low anelastic strain rates (10-13 -10-8 s-1) is expected according to the reported values by GIBELING and NIX [17] for pure FCC metals at low anelastic strain rates of 10-8-10-6 s-1.
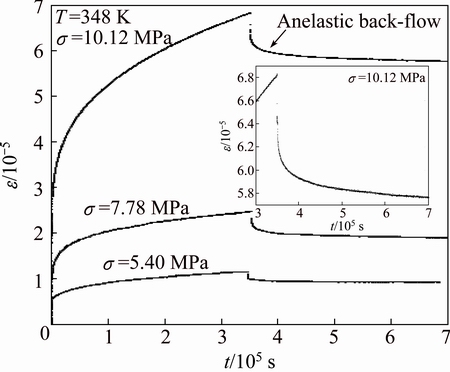
Fig. 8 Strain with time during larger stress reduction
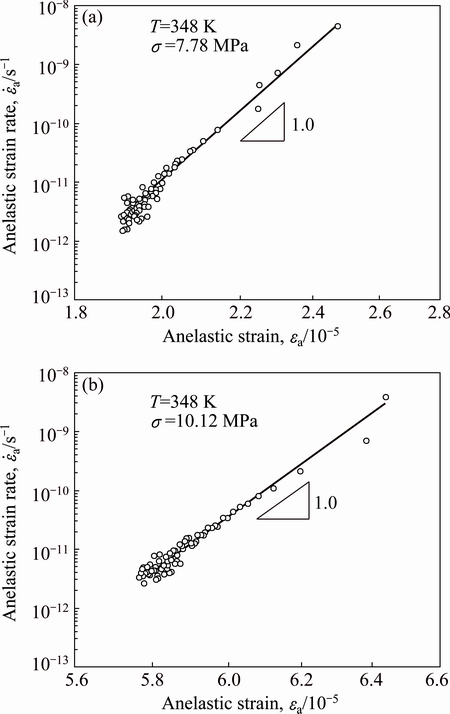
Fig. 9 Anelastic strain rate versus anelastic strain curves on logarithm scale for back-flow results in Fig. 8 at 7.78 MPa (a) and 10.12 MPa (b)
To analyze the magnitude of the anelastic back-flow process, the anelastic strain normalized by the calculated elastic strain was plotted against stress, as shown in Fig. 10. The result indicates that the anelastic strain normalized by elastic strain is independent of stress. The average ratio of anelastic strain to elastic strain is 0.14.
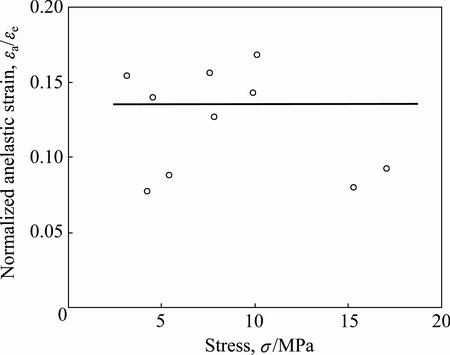
Fig. 10 Total anelastic strain εa normalized by elastic strain εe against stress at 348 K
The creep anelasticity commonly contributes to the unbowing of pinned dislocations by gliding [18,19]. For the case of a three-dimensional network of dislocations, the anelastic strain (recoverable strain), εa, is 1/6 of the calculated elastic strain, εe, [18]. The magnitude of the back-flow in this work is comparable to that predicted from this theory. Therefore, creep anelasticity in pure copper may be due to the unbowing of there-dimensional network of dislocations.
4 Conclusions
1) Transient creep behavior and anelastic back-flow in pure copper (4N Cu) with a grain size of dg=40 μm at temperatures T<0.3Tm and ultra-low creep rates 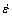 ≤ 1×10-10 s-1 were studied by a high strain resolution measurement (helicoid spring specimen technique).
≤ 1×10-10 s-1 were studied by a high strain resolution measurement (helicoid spring specimen technique).
2) Creep deformation consists of primary creep stages, and no secondary creep stage was observed.
3) Transient creep behavior was analyzed in terms of the scaling factors of the transient creep curves that were fitted by constitutive creep equations, including the power-law equation, the exponential-law equation, the logarithmic-law equation and Blackburn’s equation. Power-law creep equation is suggested to be the best to describe the creep behavior, because parameter a for power-law equation does not apparently change with elapsed time.
4) The observed anelastic strain was 1/6 of the calculated elastic strain, and linearly viscous behavior was identified from the anelastic strain rate versus anelastic strain curves on a logarithm scale (slope equals 1).
5) Creep anelasticity may be due to the unbowing of there-dimensional network of dislocations.
References
[1] KIMURA K, KUSHIMA H, SAWADA K. Long-term creep deformation property of modified 9Cr-1Mo steel [J]. Materials Science and Engineering A, 2009, 510: 58-63.
[2] KIMURA K, TODA Y, KUSHIMA H, SAWADA K. Creep strength of high chromium steel with ferrite matrix [J]. International Journal of Pressure Vessels and Piping, 2010, 87: 282-288.
[3] HANEY E M, DALLE F, SAUZAY M, VINCENT L,  I ALLAIS L, BFOURNIER B. Macroscopic results of long-term creep on a modified 9Cr-1Mo steel (T91) [J]. Materials Science and Engineering A, 2009, 510: 99-103.
I ALLAIS L, BFOURNIER B. Macroscopic results of long-term creep on a modified 9Cr-1Mo steel (T91) [J]. Materials Science and Engineering A, 2009, 510: 99-103.
[4] KLOC L,  V, VENTRUBA J. Comparison of low stress creep properties of ferritic and austenitic [J]. Materials Science and Engineering A, 2001, 319: 774-778.
V, VENTRUBA J. Comparison of low stress creep properties of ferritic and austenitic [J]. Materials Science and Engineering A, 2001, 319: 774-778.
[5] KLOC L,  V. Confirmation of low stress creep regime in 9% chromium steel by stress change creep experiments [J]. Materials Science and Engineering A, 2004, 387: 633-638.
V. Confirmation of low stress creep regime in 9% chromium steel by stress change creep experiments [J]. Materials Science and Engineering A, 2004, 387: 633-638.
[6] KLOC L, FIALA J. Harper–Dorn creep in metals at intermediate temperatures revisited: Constant structure test of pure Al [J]. Materials Science and Engineering A, 2005, 410: 38-41.
[7] KLOC L,  P. Measurement of very low creep strains: A review [J]. Journal of Testing and Evaluation, 2009, 37: 53-58.
P. Measurement of very low creep strains: A review [J]. Journal of Testing and Evaluation, 2009, 37: 53-58.
[8] ISHIBASHI M, FUJIMOTO M, IKEDA K, HATA S, NAKASHIMA H. High temperature deformation behavior of Sn based solder alloys under low stress conditions by a helical spring creep testing method [J]. The Japan Institute of Metals, 2009, 73: 373-380.
[9] TIMOSHENKO S. Elements of strength of materials [M]. 5th ed. New York: Van Nostrand Reinhold, 1968: 77-80.
[10] WAHI A M. Mechanical springs [M]. 2nd ed. New York: McGraw-Hill, 1963: 229-230.
[11] CROSSLAND I G, JONES R B, LEVTHEWAITE G W. The use of helically coiled springs in creep experiments with special reference to the case of Bingham flow [J]. Journal of Physics, 1973, 6: 1040-1046.
[12] SHEN J J, IKEDA A K, HATA S, NAKASHIMA H. Room temperature creep and substructure formation in pure aluminum at ultra-low strain rates [C]//Proceedings of the Conference of TMS2011. San Diego: Wiley, 2011: 585-592.
[13] SHEN J J, YAMASAKI S, IKEDA K, HATA S, NAKASHIMA H. Low-temperature creep at ultra-low strain rates in pure aluminum studied by a helicoid spring specimen technique [J]. Materials Transactions, 2011, 52: 1381-1387.
[14] MARUYAMA K, OIKAWA C. A new departure of long term creep curve prediction up to the tertiary stage [J]. Tetsu-to-Hagane, 1987, 73: 26-33.
[15] HOLDSWORTH S. Developments in the assessment of creep strain and ductility data [J]. Materials at High Temperatures, 2004, 21: 25-32.
[16] REED R P, SIMON N J, WALSH R P. Creep of copper: 4–300 K [J]. Materials Science and Engineering A, 1991, 147: 23-32.
[17] GIBELING J C, NIX W D. Observations of anelastic backflow following stress reductions during creep of pure metals [J]. Acta Metallurgica, 1981, 29: 1769-1784.
[18] LLOYD G J, MCELORY R J. On the anelastic contribution to creep [J]. Acta Metallurgica, 1974, 22: 339-348.
[19] LUPINC V, GABRIELLI F. Effect of grain size, particle size and γ′ volume fraction on strain relaxation in Ni-Cr base alloys [J]. Materials Science and Engineering A, 1979, 37: 143-149.
纯铜在低温和极低应变速率下的初始蠕变和粘弹性回复
申俊杰1,Ken-ichi IKEDA2, Satoshi HATA2, Hideharu NAKASHIMA2
1. 天津理工大学 机械工程学院,天津 300191;
2. Department of Electrical and Materials Science, Faculty of Engineering Sciences, Kyushu University, Kasuga, Fukuoka 816-8580, Japan
摘 要:采用高应变分辨率的螺旋弹簧蠕变试验法,研究晶粒尺寸dg为40 μm纯铜在低温(T<Tm,Tm为纯铜的熔点)和应变速率小于1×10-10 s-1条件下的蠕变和粘弹性回复行为。采用基于蠕变曲线尺度因子的数据解析法,代替传统基于外推的稳态蠕变速率的蠕变数据解析法。结果表明:纯铜低温、低应力初始蠕变行为可由幂律蠕变方程描述,因为幂律蠕变方程初始参数不随蠕变时间改变而变化;粘弹性应变为弹性应变的1/6;粘弹性应变速率的对数和粘弹性应变的对数呈线性关系(斜率为1)。因此,纯铜低温、低应力蠕变可能由三维位错网的收缩机制控制。
关键词:纯铜;蠕变;位错;粘弹性;蠕变本构方程
(Edited by Wei-ping CHEN)
Foundation item: Project (12JCYBJC32100) supported by the Tianjin Research Program of Application Foundation and Advanced Technology, China; Project ([2013]693) supported by the Scientific Research Foundation for the Returned Overseas Chinese Scholars, State Education Ministry, China
Corresponding author: Jun-jie SHEN; Tel: +86-13516233995; E-mail: sjj1982428@sina.com
DOI: 10.1016/S1003-6326(16)64285-1