DOI: 10.11817/j.issn.1672-7207.2016.01.018
基于双层优化结构的统一潮流控制器阻尼控制策略
李婷1, 2,杨波3
(1. 中南大学 信息科学与工程学院,湖南 长沙,410083;
2. 湖南广播电视大学 理工教学部,湖南 长沙,410004;
3. 武汉大学 电气工程学院,湖北 武汉,430072)
摘要:针对统一潮流控制器(UPFC)阻尼控制器在镇定信号传输存在时滞时会导致电力系统阻尼性能降低甚至失稳的问题,建立计及信号传输时滞的UPFC阻尼控制模型,提出综合考虑阻尼比和时滞稳定裕度的UPFC阻尼控制策略设计方法,将该设计问题转化为约束优化问题,并提出求解该问题的双层优化结构算法(TLOSA),其内层采用基于自由权矩阵的线性矩阵不等式(LMI)方法求解电力系统时滞稳定裕度,外层采用粒子群优化算法获取最优阻尼控制策略。研究结果表明:该算法具有保守性低和易于实现等优点;利用该方法可以获得最优的UPFC阻尼控制策略,使得电力系统既能有效阻尼低频振荡,又能容忍一定的信号传输时滞。
关键词:统一潮流控制器;时滞系统;灵活交流输电系统;辅助阻尼控制器;粒子群优化算法
中图分类号:TM712 文献标志码:A 文章编号:1672-7207(2016)01-0123-07
Damping control strategy for UPFC based on two-layer optimization structure
LI Ting1, 2, YANG Bo3
(1. School of Information Science and Engineering, Central South University, Changsha 410083, China;
2. Department of Science and Engineering, Hunan Radio & TV University, Changsha 410004, China;
3. School of Electrical Engineering, Wuhan University, Wuhan 430072, China)
Abstract: Damping controller of unified power flow controller (UPFC) may degrade its damping performance or even cause power system instability when its stabilizing signal is delayed for a certain period. Based on the newly constructed UPFC damping control model with signal transmission delay, UPFC damping control strategy design problem was discussed by taking into account of damping ratio and delay margin. The design problem was converted to a constrained optimization problem and then a two-layer optimization structure algorithm (TLOSA) was proposed to solve it. In TLOSA, delay margin was solved by free-weight matrix based linear matrix inequality (LMI) method for inner layer and optimal damping control strategy was searched by particle swarm optimization for outer layer. The results show that the proposed algorithm has low conservativeness and is easy to be implemented. The proposed algorithm can obtain optimal UPFC damping control strategy which ensures that power system can damp low frequency oscillation effectively and tolerance a certain signal transmission delay.
Key words: unified power flow controller (UPFC); time-delay system; flexible AC transmission systems (FACTS); supplementary damping controller; particle swarm optimization
统一潮流控制器(UPFC)是迄今为止功能最全的灵活交流输电装置,通过设计合理的UPFC控制器,该设备可以实现潮流控制[1]、电压控制[2]、暂态稳定控制[3]和抑制低频振荡[4]等多项功能。近年来,由于低频振荡问题严重威胁大规模电力系统安全稳定运行,利用UPFC阻尼低频振荡的研究得到了越来越多的关 注[5-6]。MOK等[7]设计了基于UPFC并联和串联换流器控制参数(m1和m2)的模糊阻尼控制器(fuzzy damping controller, FDC)阻尼联络线低频振荡,并采用遗传算法优化FDC控制策略。GUO等[8]提出采用非线性动态控制器取代传统PI控制器来控制UPFC,仅通过改变3个参数就能更有效地阻尼多种振荡模式。KANNAN等[9]设计了一种基于有功和无功的协调控制器来控制UPFC,既可在无功传输中减少节点电压的偏离,又可有效阻尼发电机的振荡。上述研究均假设阻尼控制器的镇定信号传输不存在时滞,即镇定信号从量测点到阻尼控制器之间的数据传输瞬时完成。为提高UPFC阻尼振荡的能力,与主导振荡模式相关且具有最大可观性的信号应作为辅助阻尼控制器(supplementary damping controller,SDC)的最佳候选输入信号,这些信号可能来自本地也可能来自远端。广域测量系统(wide area measurement system, WAMS)为获取这些信号提供了技术上的可行性,但是信号传输所带来的时滞也增加了SDC设计的难度[10]。这种困难体现在以下2个方面:一是在考虑信号传输时滞的情况下,UPFC阻尼控制数学模型不再是线性控制系统而是时滞系统,需要采用时滞系统稳定性分析方法取代常规线性系统分析方法对其进行研究;二是对于时滞相关镇定问题,即使对于简单的状态反馈情形,目前暂无有效的控制器综合算法[11]。因此,有必要深入研究SDC镇定信号传输被延时情形下的UPFC阻尼控制策略设计问题。解决上述问题的关键在于采用低保守性的时滞系统稳定性分析方法及采用何种算法求解最优的UPFC阻尼控制策略。自由权矩阵(free weight matrix, FWM)方法是目前国际上时滞相关控制最有效方法之一,已成功应用于非线性系统稳定性分 析[11-12]、H∞鲁棒重复控制[13]、离散时间系统等[14],能有效降低时滞电力系统稳定性分析的保守性。为此,本文作者提出采用双层优化结构算法(two-layer optimization structure algorithm, TLOSA)设计兼顾阻尼比和时滞稳定裕度的UPFC阻尼控制策略。该算法的内层采用FWM方法获取电力系统时滞相关稳定裕度,为外层优化算法的适应值评估提供基础数据。外层算法采用粒子群优化算法(particle swarm optimization, PSO)可以规避时滞相关控制器难以综合的问题,直接通过进化计算获取最优的SDC控制策略。
1 计及信号传输时滞的UPFC阻尼控制模型
计及信号传输时滞的UPFC阻尼控制模型包括开环电力系统、SDC和时滞环节3个部分,如图1所示。
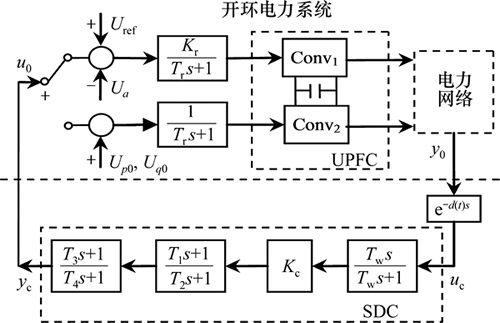
图1 计及信号传输时滞的UPFC阻尼控制模型
Fig. 1 Damping control model for UPFC under signal transmission delay
电力系统最常用的SDC由增益、隔直和超前滞后3个环节组成:
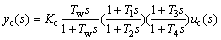 (1)
(1)
式中:yc和uc分别为输出和输入变量;s为复频率;T1,T2,T3和T4为超前滞后时间常数;Kc为增益;Tw为隔直时间常数。将式(1)由频域模型改写为状态空间模型:
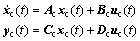 (2)
(2)
式中:xc为SDC的状态变量;Ac,Bc,Cc和Dc分别为SDC的状态、输入、输出和传递矩阵。在不考虑信号传输时滞的情形下,常采用留数方法选择具有最大模式可观度的开环电力系统输出信号作为SDC输入;采用留数相位补偿方法确定SDC参数T1,T2,T3和T4;采用根轨迹法确定SDC增益Kc。采用这种常规线性系统分析方法设计的SDC在信号传输超过一定时滞时,阻尼控制功能会大大降低甚至失效[10]。
UPFC控制机理如图2所示。装设在节点a和b之间的UPFC由激励变压器(Tsh)、并联换流器(Conv1)、直流母线电容(Cdc)、串联换流器(Conv2)、升压变压器(Tse)组成[6]。将UPFC的并联支路电流 分解为与
分解为与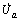 同相的分量
同相的分量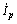 和与
和与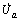 垂直的分量
垂直的分量 ,串联补偿电压
,串联补偿电压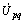 分解为与
分解为与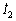 同相的分量
同相的分量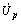 和与
和与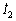 垂直的分量
垂直的分量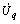 ,则
,则 和
和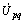 与各自分量的关系可表示为:
与各自分量的关系可表示为:
 (3)
(3)
 (4)
(4)
式中: 为输入端电压
为输入端电压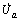 的相位;
的相位;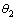 为线路电流
为线路电流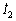 的相位。对应的并联换流器侧的输入功率Ssh和串联换流器侧的输出功率Sse分别为:
的相位。对应的并联换流器侧的输入功率Ssh和串联换流器侧的输出功率Sse分别为:
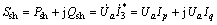 (5)
(5)
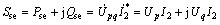 (6)
(6)

图2 UPFC控制机理
Fig. 2 UPFC control mechanism
由图2可知:SDC产生的辅助阻尼信号可通过Conv1调节UPFC的Iq为系统提供并联无功补偿,维持节点a的电压稳定;也可通过Conv2调节UPFC的Up或Uq进而调节接入端电压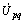 的幅值和相位,实现输电线路的串联补偿控制和节点b的电压调节等[6]。将含UPFC的开环电力系统在此稳态运行点线性化可得如下状态空间表达式:
的幅值和相位,实现输电线路的串联补偿控制和节点b的电压调节等[6]。将含UPFC的开环电力系统在此稳态运行点线性化可得如下状态空间表达式:
 (7)
(7)
式中:x0,y0和u0分别为开环电力系统的状态、输出和控制变量;A0,B0和C0分别为开环电力系统的状态、输入和输出矩阵;y0一般选择线路功率、线路电流或节点电压相位差等。由于实际电力系统中信号传输时滞d(t)具有时变和随机特征[10],设d(t)满足: (其中:t为维持系统稳定的最大时滞或称时滞稳定裕度;m为时滞的变化率)。由图1可知:uc(t)=y0(t-d(t))且u0(t)=yc(t),则考虑信号传输时滞的UPFC阻尼控制模型为
(其中:t为维持系统稳定的最大时滞或称时滞稳定裕度;m为时滞的变化率)。由图1可知:uc(t)=y0(t-d(t))且u0(t)=yc(t),则考虑信号传输时滞的UPFC阻尼控制模型为
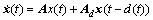 (8)
(8)
式中:
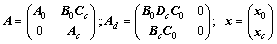
由式(8)可知,在考虑信号传输时滞的情况下,若SDC的输入信号和参数发生改变,则会引起A和Ad的变化,进而引起t的变化。因此,考虑信号传输时滞的SDC设计包含2层含义:一是在不计及信号传输时滞时阻尼比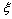 尽可能地大,这可以通过传统的线性系统特征值分析方法实现;二是系统必须满足一定的时滞稳定裕度t,即信号传输达到一定时滞时系统仍能保持稳定,这需要对系统进行时滞相关稳定性分析。
尽可能地大,这可以通过传统的线性系统特征值分析方法实现;二是系统必须满足一定的时滞稳定裕度t,即信号传输达到一定时滞时系统仍能保持稳定,这需要对系统进行时滞相关稳定性分析。
2 基于PSO的UPFC时滞阻尼控制策略求解算法
2.1 阻尼比和时滞稳定裕度的权衡
不考虑信号传输时滞时,传统的SDC设计目标一般仅考虑阻尼比;但在存在信号传输时滞时,SDC的设计目标应该兼顾阻尼比和时滞稳定裕度。根据实际控制需要,可以要求系统满足预定阻尼比x0的同时还应具有尽可能大的时滞稳定裕度。这可以保证在无信号传输时滞或时滞极小时,电力系统具有较好的阻尼性能;当发生因通信线路拥塞等原因导致信号传输时滞被延长时,电力系统仍可在一定时滞范围内保持稳定。因此,UPFC时滞阻尼控制的目标可以描述如下:
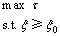 (9)
(9)
式(9)为约束优化问题,为便于PSO求解,采用罚函数法将式(9)转化为最小值无约束优化问题:
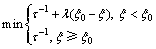 (10)
(10)
其中:l为动态罚因子,在求解式(10)的初始阶段,采用较小的l提高算法的搜索范围,后期逐步增大l以增大对不可行解的惩罚力度,确保可行解在群体进化中的优先权[15]。
2.2 外层PSO算法
PSO算法是EBERHART等[16]提出的一种用于求解优化问题的智能进化算法,已成功应用于电力变压器优化设计[17]、电压暂降监测点优化配置[18]、厂级负荷优化分配[19]等,其基本思想为:将待优化问题的每个可能解称为“粒子”,在初始化产生一群随机粒子即随机解后,粒子在搜索空间中以一定的速度飞行,并通过共享粒子个体飞行经验和群体飞行经验使整个种群向最优值进化。根据UPFC时滞阻尼控制的需要,将SDC待优化变量定义为空间中的粒子:
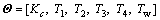 (11)
(11)
在第k次飞行时,群体中第i个粒子的状态更新方程如下:
 (12)
(12)
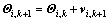 (13)
(13)
式中:vi,k为粒子当前速度;vi,k+1为更新后的粒子速度;pi,k为第i个粒子目前搜索到的最好位置;gk为群体目前搜索到的最好位置;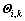 为当前粒子的位置;
为当前粒子的位置; 为更新后的粒子位置;r1和r2是[0,1]之间的随机数;k为迭代次数;c1和c2为加速因子,取值为正常数;w为惯性权重因子,用来协调与平衡算法的全局搜索和局部搜索能力;i的最大值记为imax,表示种群规模。粒子通过式(12)来不断更新自身飞行的速度和方向,通过式(13)计算新位置的坐标,直到达到最大迭代次数kmax或满足其他终止条件时停止搜索。
为更新后的粒子位置;r1和r2是[0,1]之间的随机数;k为迭代次数;c1和c2为加速因子,取值为正常数;w为惯性权重因子,用来协调与平衡算法的全局搜索和局部搜索能力;i的最大值记为imax,表示种群规模。粒子通过式(12)来不断更新自身飞行的速度和方向,通过式(13)计算新位置的坐标,直到达到最大迭代次数kmax或满足其他终止条件时停止搜索。
2.3 内层时滞稳定裕度求解算法
对于系统式(8),时滞稳定裕度可以通过时滞相关或时滞无关稳定条件求取,其中时滞相关稳定条件由于保守性更低已成为主流的求解时滞稳定裕度的方法。本文采用具有极低保守性的自由权矩阵方法获得时滞相关稳定条件并据此设计内层时滞稳定裕度求解算法[11]。
定理1 给定标量 >0和
>0和 ,若存在
,若存在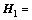
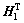 >0,
>0,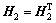 >0,
>0, >0,
>0,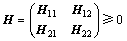 ,以及任意合适维数的矩阵N1和N2,使得如下LMI成立:
,以及任意合适维数的矩阵N1和N2,使得如下LMI成立:
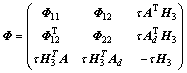 <0 (14)
<0 (14)
 (15)
(15)
则系统(8)是渐进稳定的。其中:
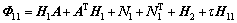
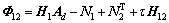
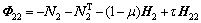
根据定理1,通过Matlab LMI Toolbox的feasp求解器可以获得系统的时滞稳定裕度,但其求解过程是通过预设t并检测待定矩阵的存在性而实现的,不利于进行PSO迭代求解。因此,根据Schur补,式(14)等价于:
 <0 (16)
<0 (16)
令 ,定理1转化为广义特征值最小化问题:
,定理1转化为广义特征值最小化问题:
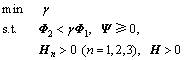 (17)
(17)
其中:

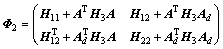
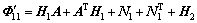
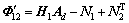
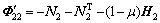
根据式(17),通过Matlab LMI Toolbox的gevp求解器可获得系统的时滞稳定裕度。为提高算法计算速度,可以采用Schur算法、Hankel算法、平衡截断算法等对含UPFC的开环电力系统式(7)先进行模型降阶得到与之等价的降阶系统,然后与SDC模型式( 2)联立形成系统式(8)的模型。
2.4 算法流程
应用双层优化结构算法TLOSA求解UPFC时滞阻尼控制策略的主要步骤如下:
1) 设置预定阻尼比x0、粒子最大迭代次数kmax和种群规模imax。
2) 建立含UPFC的开环电力系统模型,通过Matlab Schmr函数将全阶模型降阶为等价的低阶模型。通过幅频响应确定合适的低阶等价模型阶数。
3) 初始化种群,给每个粒子 随机赋予初始位置和初始速度,并确保初始种群中至少存在1个可行粒子。
随机赋予初始位置和初始速度,并确保初始种群中至少存在1个可行粒子。
4) 选择种群中第i个粒子并根据式(2)建立SDC状态空间模型,形成式(8)的时滞电力系统模型。
5) 计算阻尼比x,根据式(17)计算最大时滞稳定裕度t。
6) 根据式(10)计算适应度,更新第i个粒子目前搜索的最好位置pi,k和种群目前搜索到的最好位置gk。
7) 判断是否每个粒子都被选取到,若被选取的粒子数小于种群规模imax则转到步骤4),否则转到步骤8)。
8) 根据式(12)更新粒子位置 ,根据式(13)更新粒子速度vi,k+1。
,根据式(13)更新粒子速度vi,k+1。
9) 判断终止条件,若未达到最大迭代次数kmax则转到步骤4),否则转到步骤10)。
10) 选取最优粒子,输出SDC设计参数。
3 算例
为验证双层优化结构算法TLOSA在UPFC阻尼控制策略设计上的有效性,本文对含UPFC的两区四机系统进行了阻尼控制分析和仿真研究。图3所示为四机两区系统。图3中,UPFC安装在区域Area1和Area2间的联络线8~9上,串联补偿度为30%,Kr为75,Tr为0.005 s。该系统存在2个局部振荡和1个区间振荡。为抑制局部振荡,发电机G1和G3安装以本地发电机转速为输入的电力系统稳定器PSS1和PSS3,其传递函数模型如下:
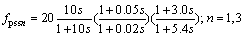 (18)
(18)
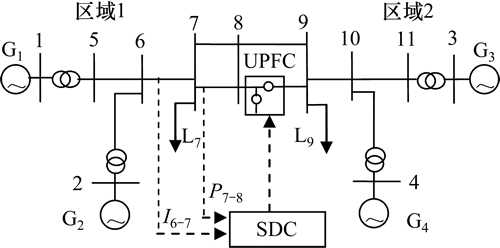
图3 四机两区系统
Fig. 3 Four-machine two-area power system
为抑制区间振荡模式,采用留数分析方法获得具有较大模式可观度的SDC输入信号为线路7~8的功率变化值DP7-8。UPFC控制信号u0分别为Up,Uq和Iq[6]。UPFC阻尼控制的目标为:最大化时滞稳定裕度t且阻尼比x≥x0=0.2。优化计算前,通过Schur函数对49阶的两区四机系统全阶模型进行降阶。图4所示为SDC输入信号为DP7-8和UPFC控制信号为Iq时的全阶系统和降阶系统的频率响应图。从图4可以看出:降阶后的7阶系统在0.1~2.0 Hz的频率范围内精确地包含了原系统的频率响应。
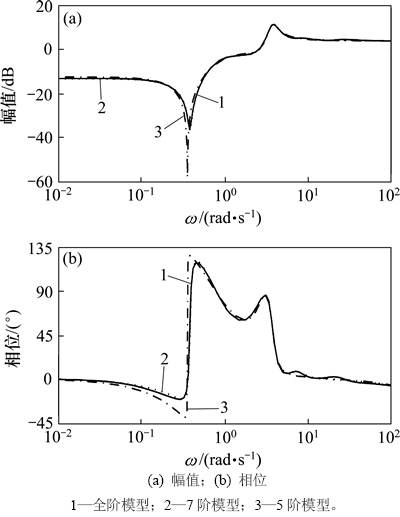
图4 全阶系统和降阶系统的频率响应
Fig. 4 Frequency response of full order and reduced order models for open loop power system
根据式(1),SDC中的Tw预先设定为10 s,T3 和T4分别等于T1和T2,则PSO待优化变量减少为3个,即Kc,T1和T2。PSO算法中c1和c2为2,imax为15,kmax为200。
计算结果如表1所示,该表结果包含Up,Uq和Iq 3种UPFC控制模式。从表1可以看出:与Up和Uq相比,Iq可以获得相对较大的时滞稳定裕度。
表1 m=0时最优UPFC阻尼控制策略
Table 1 Optimal UPFC damping control strategy for optimization objective when m=0
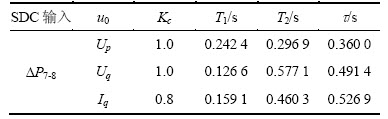
图5所示为在SDC输入信号为DP7-8,UPFC控制信号为Iq且 m=0,x0=(0.20, 0.25, 0.30)时双层优化结构算法的计算过程。从图5可见:随着预定阻尼比的增大,系统所能获得的最大时滞稳定裕度降低。
为验证双层优化结构算法结果的正确性,选取表1中最优的UPFC阻尼控制策略(Kc, T1, T2)=(0.800 0, 0.159 1, 0.460 3)进行仿真分析。仿真中开环电力系统采用49阶的全阶模型,信号传输时滞为常数时滞。实验中设定扰动模式为负荷L7的有功变化10%,仿真结果如图6所示。图6中:△P为线路8~9有功潮流变化值;t0为SDC镇定信号在传输过程中的实际时滞。从图6可以看出:对于负荷扰动而言,在信号传输时滞为0时即t0=0 s时,SDC可使系统在6 s左右内稳定,这与有SDC时系统的阻尼比x为0.209 1相符,并且该阻尼比大于优化目标中预定的阻尼比x0=0.200 0。随着t0由0逐步增大到0.526 9 s,SDC仍可使系统维持稳定,但系统的稳定性随着时滞增大而逐渐降低,其中t0取值为0.1 s至0.4 s时,系统可在10 s之内趋于稳定;t0取值为0.526 9 s时,系统在12 s之内趋于稳定;当t0取值为0.6 s时也就是t0超过计算出的最大时滞稳定裕度0.526 9 s时,SDC已不能维持系统,系统失稳。
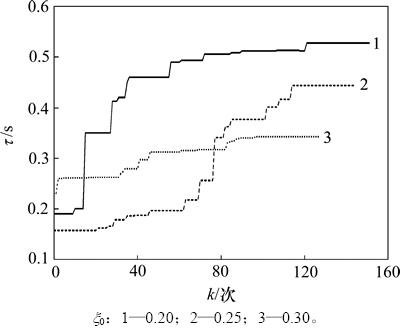
图5 双层优化结构算法的计算过程
Fig. 5 Computation procedure of two-layer optimization structure algorithm
因此,上述仿真结果表明由本文算法所得到的UPFC阻尼控制策略可以确保系统在阻尼比达到0.2以上时,还可以使系统容忍高达0.526 9 s的信号传输时滞。
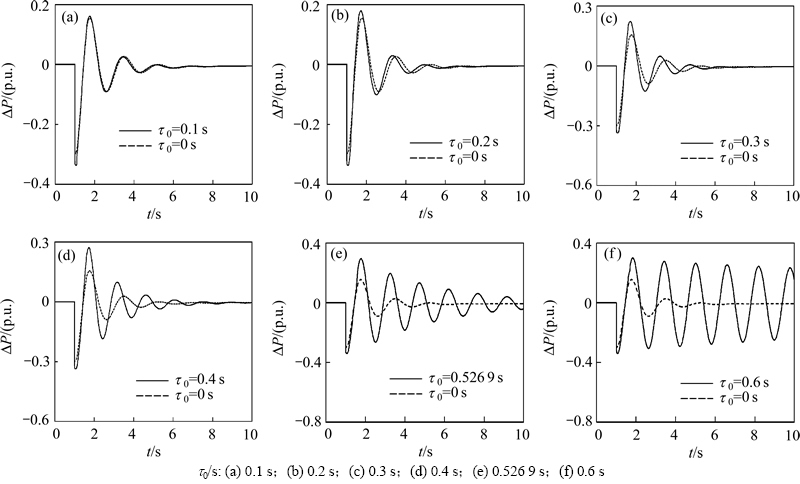
图6 负荷变化时不同时滞下线路8~9有功潮流变化规律
Fig. 6 Active power difference variation in line 8-9 under different delays for load variation
4 结论
1) 建立了一种计及信号传输时滞影响的UPFC阻尼控制模型,提出采用双层优化结构算法TLOSA设计UPFC阻尼控制策略。该算法的特点是:内层采用基于自由权矩阵的时滞相关稳定条件获取时滞稳定裕度,外层采用PSO算法获取SDC最优控制策略。
2) 双层优化结构算法TLOSA可以获得兼顾阻尼比和时滞稳定裕度的阻尼控制策略,并且内层算法中采用的FWM方法能确保该策略具有极低的保守性;可以规避时滞相关控制器难以综合的问题,直接通过外层算法中的PSO算法计算获取SDC最优控制策略。通过该算法设计的SDC可以确保电力系统在具有预定阻尼性能的同时还能容忍一定的信号传输时滞。
3) 采用双层优化结构算法TLOSA所设计的SDC控制器兼顾了实际电力系统对时滞稳定裕度和阻尼比的要求,表现出较好的阻尼性能和时滞容忍度。
参考文献:
[1] 陈众, 颜伟, 徐国禹, 等. 基于直流侧电容电压弱控制策略的UPFC二阶段控制器设计[J]. 中国电机工程学报, 2004, 24(1): 49-53.
CHEN Zhong, YAN Wei, XU Guoyu, et al. Design of UPFC two-phase controller based on DC link capacitor voltage soft control strategy[J]. Proceedings of the CSEE, 2004, 24(1): 49-53.
[2] 李兰英, 沈艳红. UPFC控制器IP设计[J]. 电力系统保护与控制, 2010, 38(11): 104-108.
LI Lanying, SHEN Yanhong. IP design of unified power flow controller [J]. Power System Protection and Control, 2010, 38(11): 104-108.
[3] GHOLIPOUR E, SAADATE S. Improving of transient stability of power systems using UPFC[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 1677-1682.
[4] ZARGHAMI M, CROW M L, JAGANNATHAN S, et al. A novel approach to interarea oscillation damping by unified power flow controllers utilizing ultracapacitors[J]. IEEE Transactions on Power Systems, 2010, 25(1): 404-412.
[5] 胡晓波, 陈中, 杜文娟, 等. 利用多端统一潮流控制器阻尼多模态振荡[J]. 电力系统自动化, 2007, 31(17): 35-39, 72.
HU Xiaobo, CHEN Zhong, DU Wenjuan, et al. Damping power system multi-mode oscillations using MUPFC[J]. Automation of Electric Power Systems, 2007, 31(17): 35-39, 72.
[6] HUANG Zhengyu, NI Yixin, SHEN C M, et al. Application of unified power flow controller in interconnected power systems-modeling, interface, control strategy, and case study[J]. IEEE Transactions on Power Systems, 2000, 15(2): 817-824.
[7] MOK T K, LIU Haoming, NI Yixin, et al. Tuning the fuzzy damping controller for UPFC through genetic algorithm with comparison to the gradient descent training[J]. Electrical Power & Energy Systems, 2005, 27(4): 275-283.
[8] GUO J, CROW M L, SARANGAPANI J. An improved UPFC control for oscillation damping[J]. IEEE Transactions on Power Systems, 2009, 24(1): 288-296.
[9] KANNAN S, JAYARAM S, SALAMA M M A. Real and reactive power coordination for a unified power flow controller[J]. IEEE Transactions on Power Systems, 2004, 19(3): 1454-1461.
[10] STAHLHUT J W, BROWNE T J, HEYDT G T, et al. Latency viewed as a stochastic process and its impact on wide area power system control signals[J]. IEEE Transactions on Power Systems, 2008, 23(1): 84-91.
[11] HE Yong, WANG Qingguo, LIN Chong, et al. Delay-range- dependent stability for systems with time-varying delay[J]. Automatica, 2007, 43(2): 371-376.
[12] HE Yong, WANG Qingguo, XIE Lihua, et al. Further improvement of free-weighting matrices technique for systems with time-varying delay[J]. IEEE Transactions on Automatic Control, 2007, 52(2): 293-299.
[13] WU Min, ZHOU Lan, SHE Jinhua. Design of observer-based H∞ robust repetitive-control system[J]. IEEE Transactions on Automatic Control, 2011, 6(56): 1452-1457.
[14] HE Yong, WU Min, LIU Guoping, et al. Output feedback stabilization for a discrete-time system with a time-varying delay[J]. IEEE Transactions on Automatic Control, 2008, 53(10): 2372-2377.
[15] DEL VALLE Y, VENAYAGAMOORTHY G K, MOHAGHEGHI S, et al. Particle swarm optimization: Basic concepts, variants and applications in power systems[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(2): 171-195.
[16] EBERHART R, KENNEDY J. A new optimizer using particle swarm theory[C]// Proceedings of the Sixth International Symposium on Micro Machine and Human Science. Nagoya, Japan: IEEE, 1995: 39-43.
[17] 潘再平, 张震, 潘晓弘. 基于QPSO算法的电力变压器优化设计[J]. 电工技术学报, 2013, 28(11): 42-47.
PAN Zaiping, ZHANG Zhen, PAN Xiaohong. Optimal design of Power transformers Using quantum-behaved particle swarm optimization[J]. Transactions of China Electrotechnical Society, 2013, 28(11): 42-47.
[18] 周超, 田立军. 基于粒子群优化算法的电压暂降监测点优化配置[J]. 电工技术学报, 2014, 29(4): 181-187.
ZHOU Chao, TIAN Lijun. An optimum allocation method of voltage sag monitoring nodes based on particle swarm optimization algorithm[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 181-187.
[19] 司风琪, 顾慧, 叶亚兰, 等. 基于混沌粒子群算法的火电厂厂级负荷在线优化分配[J]. 中国电机工程学报, 2011, 31(26): 103-109.
SI Fengqi, GU Hui, YE Yalan, et al. Online unit load economic dispatch based on chaotic-particle swarm optimization algorithm[J]. Proceedings of the CSEE, 2011, 31(26): 103-109.
(编辑 罗金花)
收稿日期:2015-08-15;修回日期:2015-10-17
基金项目(Foundation item):国家自然科学基金资助项目(51007042, 51577136);湖南省教育厅科研项目(14C0782) (Projects(51007042, 51577136) supported by the National Natural Science Foundation of China; Project(14C0782) supported by the Scientific Research of Education Department of Hunan Province)
通信作者:杨波,博士,研究员,从事电力系统稳定与控制研究;E-mail: yasom@126.com