高压高温下Re2N的弹性和热力学性能
来源期刊:中国有色金属学报(英文版)2013年第12期
论文作者:张美光 闫海燕 魏 群 黄多辉
文章页码:3714 - 3721
关键词:Re2N;过渡金属氮化物;弹性性能;热力学性能
Key words:Re2N; transition metal nitrides; elastic properties; thermodynamic properties
摘 要:采用基于密度泛函理论的第一性原理计算方法,系统研究高压高温下Re2N的晶体参数、力学性能和热力学性能。结果表明:在高压下Re2N具有明显的弹性各向异性,与弹性常数 C12、 C13、C44相比,C11和C33的变化随着压力的变化非常明显。此外,首次计算Re2N的体弹模量B、弹性模量E和剪切模量G沿不同晶轴的分布。弹性模量在一些主要晶轴方向上的大小分布趋势如下: 。计算结果还表明:在(0001)晶面,Re2N的抗剪切能力是最低的,从而极大地减小对大剪切变形的阻力。基于准简谐德拜模型,在0~50 GPa压力和0~1600 K温度下得到德拜温度、格林艾森参数、热传导以及热扩散系数的变化行为。
Abstract: First principles calculations are preformed to systematically investigate the elastic and thermodynamic properties of Re2N at high pressure and high temperature. The Re2N exhibits a clear elastic anisotropy and the elastic constants C11 and C33 vary rapidly in comparison with the variations in C12, C13 and C44 at high pressure. In addition, bulk modulus B, elastic modulus E, and shear modulus G as a function of crystal orientations for Re2N are also investigated for the first time. The tensile directional dependences of the elastic modulus obey the following trend: . The shear moduli of Re2N within the (0001) basal plane are the smallest and greatly reduce the resistance of against large shear deformations. Based on the quasi-harmonic Debye model, the dependences of Debye temperature, Grüneisen parameter, heat capacity and thermal expansion coefficient on the temperature and pressure are explored in the whole pressure range from 0 to 50 GPa and temperature range from 0 to 1600 K.
Trans. Nonferrous Met. Soc. China 23(2013) 3714-3721
Mei-guang ZHANG1, Hai-yan YAN2, Qun WEI3, Duo-hui HUANG4
1. Department of Physics and information Technology, Baoji University of Arts and Sciences, Baoji 721016, China;
2. College of Chemistry and Chemical Engineering, Baoji University of Arts and Sciences, Baoji 721013, China;
3. School of Physics and Optoelectronic Engineering, Xidian University, Xi’an 710071, China;
4. Computational Physics Key Laboratory of Sichuan Province, Yibin University, Yibin 644007, China
Received 24 September 2012; accepted 14 April 2013
Abstract: First principles calculations are preformed to systematically investigate the elastic and thermodynamic properties of Re2N at high pressure and high temperature. The Re2N exhibits a clear elastic anisotropy and the elastic constants C11 and C33 vary rapidly in comparison with the variations in C12, C13 and C44 at high pressure. In addition, bulk modulus B, elastic modulus E, and shear modulus G as a function of crystal orientations for Re2N are also investigated for the first time. The tensile directional dependences of the elastic modulus obey the following trend: 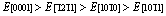 . The shear moduli of Re2N within the (0001) basal plane are the smallest and greatly reduce the resistance of against large shear deformations. Based on the quasi-harmonic Debye model, the dependences of Debye temperature, Grüneisen parameter, heat capacity and thermal expansion coefficient on the temperature and pressure are explored in the whole pressure range from 0 to 50 GPa and temperature range from 0 to 1600 K.
. The shear moduli of Re2N within the (0001) basal plane are the smallest and greatly reduce the resistance of against large shear deformations. Based on the quasi-harmonic Debye model, the dependences of Debye temperature, Grüneisen parameter, heat capacity and thermal expansion coefficient on the temperature and pressure are explored in the whole pressure range from 0 to 50 GPa and temperature range from 0 to 1600 K.
Key words: Re2N; transition metal nitrides; elastic properties; thermodynamic properties
1 Introduction
Transition metal nitrides are of great interest in both fundamental science and technological applications because of their unusual physical and chemical properties [1-3]. Traditional applications have taken advantage of the hard and refractory nature of many early transition metal nitrides, such as TiN, CrN and HfN. In contrast, not too much success has been achieved in exploring the late transition metal nitrides, especially for platinum group and noble metals nitrides. Until recently, a significant progress in synthesis of the dinitrides of Pt, Ir, Os, and Pd has been made at extreme conditions (approximately 50 GPa and 2000 K) [4-7]. These nitrides have been shown to possess ultrahigh bulk moduli (428 GPa for IrN2) comparable with those of the traditional superhard materials, thus exhibiting interesting mechanical properties. Extensive studies [8-13] are therefore carried out in order to hunt for new potential superhard transition metal nitrides.
More recently, FRIEDRICH et al [14] have succeeded in synthesizing two novel rhenium nitrides (Re2N and Re3N) and characterized them using white beam Laue microdiffraction. Both hexagonal phases have very high bulk moduli (> 400 GPa); close to that of c-BN and higher than that of ReB2. Between these two nitrides, the Re2N adopts hexagonal structures with a space group P63/mmc, and the atomic positions are Re (1/3, 2/3, 0.106) and N (1/3, 2/3, 3/4). Following this exciting work, FRIEDRICH et al [15] and DELIGOZ et al [16] investigated the vibrational properties of the hexagonal Re2N. ZHANG et al [17] later have studied the thermodynamic stability and mechanical properties as well as a bond deformation mechanism of Re2N. The structural, electronic, and elastic properties of Re2N have been also investigated at ambient conditions [18-21], and the Re2N was found to be an ultra-incompressible and hard material due to its high bulk modulus, originating from the strong Re-N covalent bonds. Very recently, SOTO et al [22] have systematically investigated two classes of variable-composition rhenium nitride: 1) interstitial rhenium nitride as a solid solution and 2) rhenium nitride in lamellar structures. They pointed out that Re2N phase belongs to the second class and possesses the higher stability compared to the interstitial phases. Up to now, the properties of hexagonal Re2N under ambient pressure are basically clear, but those under high pressures have never been fully investigated.
In this work, the elastic and thermodynamic properties of hexagonal Re2N under high pressure are investigated to provide some additional information to the existing data on the physical properties of Re2N. In addition, the elastic anisotropy of crystals can exert great effects on the properties of physical mechanism, such as anisotropic plastic deformation, crack behavior and elastic instability. Compared to previous works, we extend the mechanical properties and present in detail the elastic moduli as a function of crystal orientation for Re2N at ambient pressure and high pressure in order to further clarify mechanical properties of Re2N. The calculated results indicate that the (0001) plane may be the cleavage plane of Re2N which was attributed to the presence of soft metallic Re-Re layers.
2 Computational methods
All calculations are performed based on the plane-wave pseudopotential density function theory, as implemented in CASTEP package [23]. Vanderbilt ultrasoft pseudopotentials [24] are employed to describe the electron-ion interactions. The exchange correlation energy is described in the generalized gradient approximation (GGA) using the Perdew-Burke- Ernzerhof (PBE) functional [25]. The structure is optimized with the Broyden-Fletcher-Goldfarb-Shanno (BFGS) [26] method. Pseudo-atomic calculations are performed for Re 5s25p66s25d 5 and N 2s22p3. In the structure calculation, the electronic wave functions are expanded in plane-wave basis set with cutoff energy of 520 eV, and the special points sampling integration over the Brillouin zone was employed by the Monkhorst-Pack method [27] with a grid of 0.03 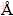 -1. The self-consistent convergence of the total energy is 10-7 eV/atom and the maximum force on the atom is 10-3 eV/
-1. The self-consistent convergence of the total energy is 10-7 eV/atom and the maximum force on the atom is 10-3 eV/ 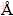 . Furthermore, the quasi-harmonic Debye model [28], which is constructed from the Helmholtz free energy at the temperature below the melting point in the quasi-harmonic approximation, is applied to obtaining thermodynamic properties of Re2N.
. Furthermore, the quasi-harmonic Debye model [28], which is constructed from the Helmholtz free energy at the temperature below the melting point in the quasi-harmonic approximation, is applied to obtaining thermodynamic properties of Re2N.
3 Results and discussion
3.1 Structural parameters of Re2N
The equilibrium structural parameters for Re2N were obtained by full relaxations of both lattice constants and internal atomic coordinations without any restrictions at ambient pressure. The optimized lattice constants are a0=2.855 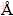 and c0=9.849
and c0=9.849 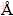 , which are in good agreement with the experimental values of a=2.835
, which are in good agreement with the experimental values of a=2.835 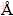 and c=9.881
and c=9.881 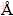 . The calculated a0 and c0 deviate from the corresponding experimental values are within 0.7% and 0.3%, respectively. In addition, these predicted lattice parameters also agree well with the previous theoretical values [16-21]. Therefore, the excellent agreements above support the reliability of the computational procedure employed in the present work. In order to provide some insights into the pressure behavior of Re2N, the pressure acting on the system as a function of lattice parameters (a/a0 and c/c0) and unit cell volume (V/V0) as well as c-BN are obtained and plotted in Fig. 1, where a0, c0 and V0 are the equilibrium structural parameters at zero pressure. Firstly, the volume incompressibility of Re2N exceeds that of c-BN at high pressure, indicating its ultra-incompressible nature. Secondly, by fitting these calculated data with the least squares method, the relationships at the temperature of 0 K are obtained as the following relationsships:
. The calculated a0 and c0 deviate from the corresponding experimental values are within 0.7% and 0.3%, respectively. In addition, these predicted lattice parameters also agree well with the previous theoretical values [16-21]. Therefore, the excellent agreements above support the reliability of the computational procedure employed in the present work. In order to provide some insights into the pressure behavior of Re2N, the pressure acting on the system as a function of lattice parameters (a/a0 and c/c0) and unit cell volume (V/V0) as well as c-BN are obtained and plotted in Fig. 1, where a0, c0 and V0 are the equilibrium structural parameters at zero pressure. Firstly, the volume incompressibility of Re2N exceeds that of c-BN at high pressure, indicating its ultra-incompressible nature. Secondly, by fitting these calculated data with the least squares method, the relationships at the temperature of 0 K are obtained as the following relationsships:
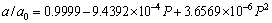 (1)
(1)
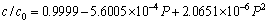 (2)
(2)
 (3)
(3)
It can be seen that the incompressibility along the c-axis is larger than that along the a-axis, suggesting its clear elastic anisotropy.
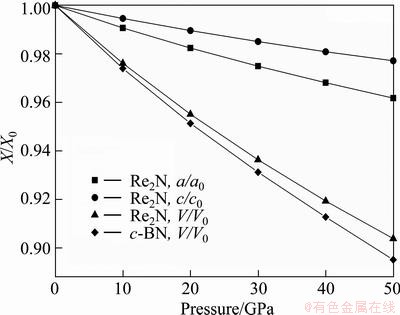
Fig. 1 Normalized parameters a/a0, c/c0, and V/V0 as a function of pressure for Re2N
3.2 Elastic properties of Re2N
The elastic constants of a material describe its response to applied stress and provide useful information about its bonding character. For the hexagonal Re2N, the matrix of its elastic stiffness constants contains five independent elements Cij (C11, C12, C13, C33, and C44). The elastic constants of Re2N at zero pressure were calculated by the strain-stress method, meanwhile, the corresponding elastic compliance constants sij can be obtained using the relations between elastic compliance constants and the elastic constants suggested by NYE [29]. The calculated values of Cij and sij are collected in Table 1. Also the results obtained in previous theoretical works are included. For Re2N, there are no available experimental data; however, taking account of the excellent agreements of our calculated results and the other theoretical values, our predicted values should be reliable. Furthermore, the key criterion for mechanical stability of a crystal is that strain energy must be positive, that is in a hexagonal crystal [30]: C33>0, C44>0, C12>0, C11>|C12|, (C11+2C12)C33>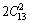 . According to the above criteria, it is clear that Re2N is mechanically stable at ambient condition. To further illustrate the effect of pressure on the elastic properties of Re2N, the variations of elastic constants with pressure are shown in Fig. 2. As shown in Fig. 2, five independent elastic constants increase monotonically with pressure. Meanwhile, the predicted pressure derivatives of elastic constants,
. According to the above criteria, it is clear that Re2N is mechanically stable at ambient condition. To further illustrate the effect of pressure on the elastic properties of Re2N, the variations of elastic constants with pressure are shown in Fig. 2. As shown in Fig. 2, five independent elastic constants increase monotonically with pressure. Meanwhile, the predicted pressure derivatives of elastic constants,  C11/
C11/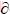 P,
P, 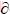 C12/
C12/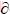 P,
P, 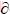 C13/
C13/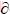 P,
P, 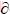 C33/
C33/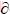 P and
P and 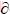 C44/
C44/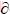 P for Re2N are found to be 5.65, 3.03, 4.25, 4.68 and 1.89, respectively. These results indicate that C11 and C33 vary rapidly under the effect of pressure in comparison with the variations in C12, C13 and C44, which is the same as the case for Re3N [31]. It indicates that C11 and C33 are sensitive to pressure compared with C12, C13 and C44. Furthermore, the calculated elastic constants under pressure up to 50 GPa also satisfy the well-known Born stability criteria, indicating that Re2N under pressure is also mechanically stable.
P for Re2N are found to be 5.65, 3.03, 4.25, 4.68 and 1.89, respectively. These results indicate that C11 and C33 vary rapidly under the effect of pressure in comparison with the variations in C12, C13 and C44, which is the same as the case for Re3N [31]. It indicates that C11 and C33 are sensitive to pressure compared with C12, C13 and C44. Furthermore, the calculated elastic constants under pressure up to 50 GPa also satisfy the well-known Born stability criteria, indicating that Re2N under pressure is also mechanically stable.
Like the elastic constants, the bulk modulus, shear modulus, and elastic modulus contain information regarding the hardness of a material with respect to various types of deformation. Bulk modulus B measures the resistance of a material to volume changes and provides an estimate of its response to a hydrostatic pressure. Shear modulus G describes the resistance of a material to shape change. Elastic modulus E measures the resistance against uniaxial tensions. These are important parameters for defining the mechanical properties of a material. For engineering applications that make use of single crystals, it is necessary to know these elastic moduli as a function of crystal orientation. As outlined by PANDA and RAVI CHANDRAN [32] and HE et al [33], executing the appropriate coordinate system transformations for the compliances allows the determination of the variation of bulk modulus, elastic moduli, and shear modulus with crystallographic direction [uvw] for a given crystallographic plane (hkl) containing these directions (i.e., B[uvw], E[uvw], and G(hkl)[uvw]) are obtained. For the hexagonal Re2N, the bulk modulus B and elastic modulus E can be expressed as follows:
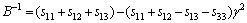 (4)
(4)
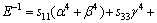

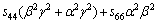 (5)
(5)
where α, β and γ are the direction cosines of [uvw] direction. The shear modulus G on the (hkl) shear plane with shear stress applied along [uvw] direction is given by
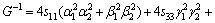
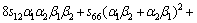
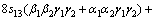
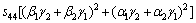 (6)
(6)
where α1, β1, γ1, α2, β2 and γ2 are the direction cosines of the [uvw] and [HKL] directions in the coordinate systems, and the [HKL] denotes the vector normal to the (hkl) shear plane.
Table 1 Calculated elastic constants Cij and elastic compliance constants sij of Re2N
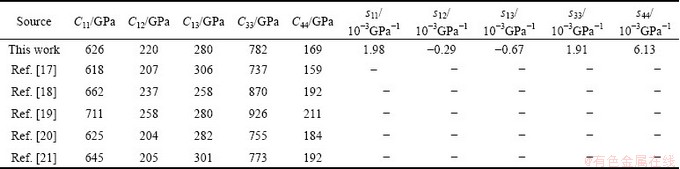
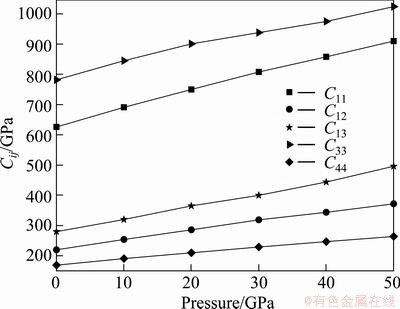
Fig. 2 Pressure dependences of Cij for Re2N
Figures 3(a) and (b) illustrate the directional dependence of the bulk modulus and elastic modulus of Re2N using Eqs. (4) and (5). The plane projections of the directional dependence of the bulk modulus and elastic modulus are also shown in Figs. 3(c) and (d) for comparison. It can be seen that the nonspherical nature of Re2N in Figs. 3(a) and (b) shows the clear anisotropy of the bulk modulus and elastic modulus. Moreover, while in-plane anisotropy in ab plane is nonexistent, a significant in-plane elastic anisotropy in ac plane is revealed in Figs. 3(c) and (d). This is consistent with the hexagonal symmetry of ab plane where Re-Re and N-N bonds exist in ‘graphite-like’’ layers alternatively stacked in the c-direction. The bulk modulus in the c-direction (B[0001]) is significantly higher than in other two directions (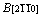 and
and  ), which is in agreement with the calculated elastic constants in Table 1. In order to get a better understanding of the origin of the changes in elastic modulus along different directions, the orientation dependence of elastic modulus is calculated when the tensile axis is within specific planes, as shown in Fig. 4(a). For elastic modulus in the (0001) plane, let θ to be the angle between tensile stress and
), which is in agreement with the calculated elastic constants in Table 1. In order to get a better understanding of the origin of the changes in elastic modulus along different directions, the orientation dependence of elastic modulus is calculated when the tensile axis is within specific planes, as shown in Fig. 4(a). For elastic modulus in the (0001) plane, let θ to be the angle between tensile stress and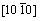 . From Eq. (5), it obtains
. From Eq. (5), it obtains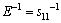 . This indicates that elastic modulus on the basal plane is independent of tensile stress direction, which is a result of the isotropy of elasticity in the basal plane for hexagonal crystal. These results are also in agreement with the results shown in Fig. 3(d). For the orientation dependence of elastic modulus from [0001] (θ=0°) to
. This indicates that elastic modulus on the basal plane is independent of tensile stress direction, which is a result of the isotropy of elasticity in the basal plane for hexagonal crystal. These results are also in agreement with the results shown in Fig. 3(d). For the orientation dependence of elastic modulus from [0001] (θ=0°) to 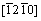 (θ=90°) on the prismatic plane
(θ=90°) on the prismatic plane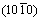 , the Re2N possess a maximum of E[1000] and a minimum of
, the Re2N possess a maximum of E[1000] and a minimum of 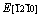 . For the pyramidal plane
. For the pyramidal plane 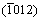 in Fig. 4(a), it displays the variation of elastic modulus with Emax along
in Fig. 4(a), it displays the variation of elastic modulus with Emax along 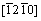 directions and Emin along
directions and Emin along 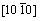 directions. For the pyramidal
directions. For the pyramidal 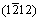 plane elastic moduli E behave again very similar for the directions between
plane elastic moduli E behave again very similar for the directions between 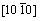 and
and 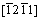 with a minimum of
with a minimum of  and a maximum of
and a maximum of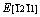 . Therefore, the ordering of elastic modulus as a function of the principal crystal tensile [uvw] for Re2N is:
. Therefore, the ordering of elastic modulus as a function of the principal crystal tensile [uvw] for Re2N is: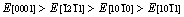 .
.

Fig. 3 Illustrations of directional dependence of bulk modulus (a) and elastic modulus (b) for Re2N, projections in different planes of directional dependent bulk modulus (c) and elastic modulus (d) for Re2N
To understand plastic deformation in Re2N on a fundamental level, the shear moduli on the (hkl) shear planes with shear stress applied along [uvw] directions are plotted in Fig. 4(b). Firstly, the shear modulus of Re2N is independent of the shear directions from 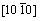 to
to 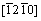 directions within (0001) basal plane. More importantly, the shear modulus within the (0001) basal plane for Re2N is the smallest, where the corresponding shear deformation involves a shear displacement between pure Re-Re metallic bonding layers in this plane. This result demonstrates that the (0001) plane may be the cleavage plane of Re2N and is also in agreement with the ideal shear strengths calculation performed by ZHANG et al [17]. Secondly, the shear modulus within prismatic shear plane
directions within (0001) basal plane. More importantly, the shear modulus within the (0001) basal plane for Re2N is the smallest, where the corresponding shear deformation involves a shear displacement between pure Re-Re metallic bonding layers in this plane. This result demonstrates that the (0001) plane may be the cleavage plane of Re2N and is also in agreement with the ideal shear strengths calculation performed by ZHANG et al [17]. Secondly, the shear modulus within prismatic shear plane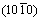 increases with the shear stress direction rotating from
increases with the shear stress direction rotating from 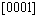 to
to 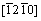 directions, while on the contrary it decreases with the shear stress direction rotating from
directions, while on the contrary it decreases with the shear stress direction rotating from 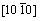 to
to 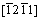 directions within pyramidal plane
directions within pyramidal plane 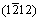 . Thirdly, the shear modulus of Re2N remains nearly invariant within pyramidal plane
. Thirdly, the shear modulus of Re2N remains nearly invariant within pyramidal plane 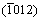 with the shear stress direction rotating from
with the shear stress direction rotating from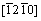 to
to 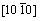 directions. This suggests that the shape change in the
directions. This suggests that the shape change in the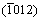 plane with any shear stress directions is very small.
plane with any shear stress directions is very small.
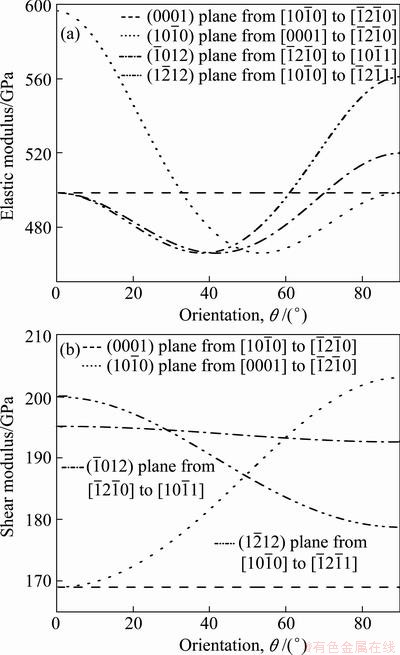
Fig. 4 Plots of elastic modulus E for different crystallographic directions [uvw] (a) and shear modulus G for different crystallographic directions [uvw] in various low-index planes [hkl] (b) for Re2N
3.3 Thermodynamic properties of Re2N
The investigation on the thermodynamic properties of solid at high pressure and high temperature is an interesting topic in the condensed matter physics. Compared to PtN2 [34], PtN [35] and Re3N [31], there are very limited theoretical works on the thermodynamic properties for Re2N at high pressure and high temperature. The thermal properties of Re2N are determined in the temperature range from 0 to 1600 K, where the quasi-harmonic model remains fully valid. The pressure effect is investigated in the range of 0 to 50 GPa. In the quasi-harmonic Debye model, the Debye temperature Θ and the Grüneisen parameter γ are two key quantities. The Debye temperature closely relates to many physical properties of solids, such as specific heat, dynamic properties, and melting temperature. The Grüneisen parameter describes the anharmonic effects in the vibrating lattice, and it has been widely used to characterize and extrapolate the thermodynamic behavior of a material at high pressure and high temperature. The Debye temperature and the Grüneisen parameter at various temperatures (0, 300, 600, 900 and 1500 K) and different pressures (0, 10, 20, 30, 40 and 50 GPa) are listed in Table 2. It should be noted that our calculated Debye temperature at T=0 K and P=0 GPa is 462.6 J/(mol·K-1) which is close to 474.8 J/(mol·K-1) calculated by elastic constants, confirming the validity of quasi-harmonic model applied here. From Table 2, it can be found that when the applied pressure changes from 0 to 50 GPa, the Debye temperature increases by 19.6%, 24.2%, 25.1%, 26.1%, and 28.2%, and the Grüneisen parameter decreases by 14.2%, 14.5%, 15.1%, 15.6%, and 16.9% at temperatures of 0, 300, 600, 900, and 1500 K, respectively. It indicates that, when the temperature is kept constant, the Grüneisen parameter decreases with increasing applied pressure, in virtue of the fact that the effect of increasing pressure on the material is the same as decreasing temperature of the material. On the other hand, the Debye temperature decreases almost linearly with temperature at certain pressure.
Table 2 Calculated Debye temperature Θ (in K) and Grüneisen parameter γ of Re2N at different pressures and different temperatures

Heat capacity belongs to one of the most important thermodynamic properties of solids. It is intimately related to the temperature dependence of fundamental thermodynamic functions, and it is of key importance for linking thermodynamics with microscopic structure and dynamics. The calculated heat capacity at constant pressure Cp and heat capacity at constant volume CV with the temperature and pressure are shown in Fig. 5. The difference between Cp and CV is very small at low temperatures (T<300 K). However, at high temperatures, the CV approaches a constant value, while Cp increases monotonously with increments of the temperature. It is also interesting to note that the values of CV follow the Debye model at low temperature due to the anharmonic approximations. However, the anharmonic effect on CV is suppressed and the CV is close to a constant at sufficient high temperatures, obeying Dulong and Petit’s rule. In a word, it can be seen that the heat capacity increases with the temperature at the same pressure and decreases with the pressure at the same temperature. The effects of the temperature on the heat capacity are much more significant than that of the pressure on it. The thermal expansion coefficient α dependented on temperature and pressure is also shown in Fig. 6. Figure 6 shows that the thermal expansion coefficient α increases quickly with the temperature at T< 300 K under different pressures. As pressure increases, the thermal expansion coefficient decreases rapidly and the effects of temperature become less and less pronounced, resulting in linear high- temperature behavior. At constant temperature, for instance T=600 K, it changes linearly with pressure following a gently decreasing trend.
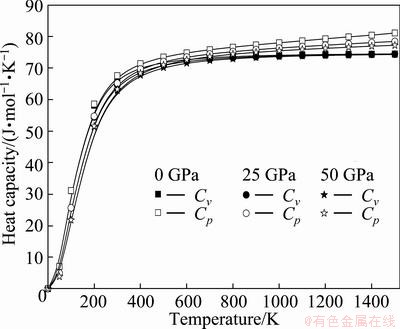
Fig. 5 Temperature dependences of heat capacity at different pressures for Re2N
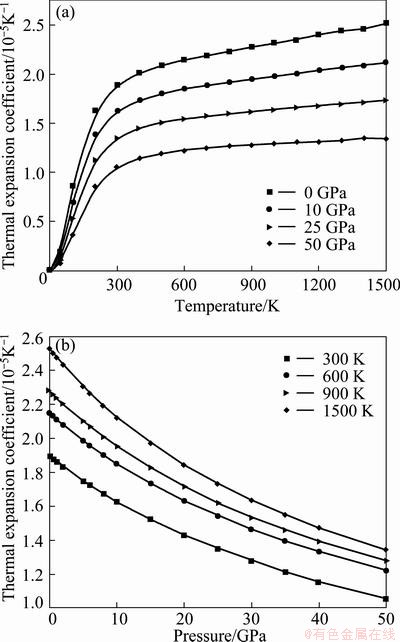
Fig. 6 Pressure (a) and temperature (b) dependences of isothermal bulk modulus for Re2N
4 Conclusions
1) The calculated lattice parameters by GGA method are in excellent agreement with the experimental data and previous theoretical values for Re2N. The incompressibility of Re2N along the c-axis is larger than that along the a-axis under high pressure.
2) The Re2N is found to be mechanically stable up to 50 GPa and the elastic constants C11 and C33 vary rapidly under the effect of pressure in comparison with the variations in C12, C13 and C44.
3) The tensile directional dependences of the elastic modulus E have been investigated for the first time, and the results show 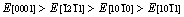 for these principal crystal directions. The shear modulus of Re2N within the (0001) basal plane is the smallest, where the corresponding shear deformation involves a shear displacement between pure Re layers in this plane.
for these principal crystal directions. The shear modulus of Re2N within the (0001) basal plane is the smallest, where the corresponding shear deformation involves a shear displacement between pure Re layers in this plane.
4) Using quasi-harmonic Debye model, the thermodynamic properties including the Debye temperature, Grüneisen parameter, heat capacity, and thermal expansion coefficient of Re2N are predicted under high pressure and high temperature.
References
[1] Jhi S H, Ihm J, Louie S G, Cohen M L. Electronic mechanism of hardness enhancement in transition-metal carbonitrides [J]. Nature, 1999, 399: 132-134.
[2] Zerr A, Miehe G, Riedel R. Synthesis of cubic zirconium and hafnium nitride having Th3P4 structure [J]. Nat Mater, 2003, 2(3): 185-189.
[3] Horvath-Bordon E, Riedel R, Zerr A, McMillan P F, Auffermann G, Prots Y, Bronger W, Kniep R, Kroll P. High-pressure chemistry of nitride-based materials [J]. Chem Soc Rev, 2006, 35: 987-1014.
[4] Gregoryanz E, Sanloup C, Somayazulu M, Badro J, Fiquet G, Mao H K, Hemley R J. Synthesis and characterization of a binary noble metal nitride [J]. Nat Mater, 2004, 3: 294-297.
[5] Crowhurst J C, Goncharov A F, Sadigh B, Evans C L, Morrall P G, Ferreira J L, Nelson A J. Synthesis and characterization of the nitrides of platinum and iridium [J]. Science, 2006, 311(5765): 1275-1278.
[6] Young A F, Sanloup C, Gregoryanz E, Scandolo S, Hemley R J, Mao H K. Synthesis of novel transition metal nitrides IrN2 and OsN2 [J]. Phys Rev Lett, 2006, 96: 155501.
[7] Crowhurst J C, Goncharov A F, Sadigh B, Zaug J M, Aberg D, Meng Y, Prakapenka V B. Synthesis and characterization of nitrides of iridium and palladium [J]. J Mater Res, 2008, 23(1): 1-5.
[8] Yu R, Zhan Q, De Jonghe L C. Crystal structures of and displacive transitions in OsN2, IrN2, RuN2, and RhN2 [J]. Angew Chem Int Ed, 2007, 46: 1136-1140.
[9] Yao Z W, Zhang A J, Li Y, Zhang Y Z, Cheng X Q, Shi C. An investigation of the thermal stability, crystal structure and catalytic properties of bulk and alumina-supported transition metal nitrides [J]. J Alloys Compd, 2008, 464 (1-2): 488-496.
[10] Aberg D, Sadigh B, Crowhurst J, Goncharov A F. Mechanism for superelongation of carbon nanotubes at high temperatures [J]. Phys Rev Lett, 2008, 100: 095501.
[11] Guo J, Sun Z M, Ahuja M. Ab initio study of the phase stability and mechanical properties of 5d transition metal nitrides MN2 [J]. J Alloys Compd, 2009, 472(1-2): 425-428.
[12] Wang H, Li Q, Li Y W, Xu Y, Cui T, Oganvo A R, Ma Y M. Ultra-incompressible phases of tungsten dinitride predicted from first principles [J]. Phys Rev B, 2009, 79: 132109.
[13] Chen W, Jiang J Z. Elastic properties and electronic structures of 4d- and 5d-transition metal mononitrides [J]. J Alloys Compd, 2010, 499 (2): 243-254.
[14] Friedrich A, Winkler B, Bayarjargal L, Morgenroth W, Juarez-Arellano E A, Milman V, Refson K, Kunz M Chen, K. Novel rhenium nitrides [J]. Phys Rev Lett, 2010, 105: 085504.
[15] Friedrich A, Winkler B, Refson K, Milman V. Vibrational properties of Re3N from experiment and theory [J]. Phys Rev B, 2010, 82: 224106.
[16] Deligoz E, Colakoglu K, Ozisik H B, Ciftci Y O. Vibrational properties of Re2N and Re3N compounds [J]. Solid State Commun, 2011, 151(17): 1122-1127.
[17] Zhang R F, Lin Z J, MAO H K, ZHAO Y S. Thermodynamic stability and unusual strength of ultra-incompressible rhenium nitrides [J]. Phys Rev B, 2011, 83: 060101.
[18] Bannikov V V, Shein I R, Ivanovskii A L. Elastic and electronic properties of hexagonal rhenium sub-nitrides Re3N and Re2N in comparison with hcp-Re and wurtzite-like rhenium mononitride ReN [J]. Phys Status Solidi B, 2011, 248(6): 1369-1374.
[19] Hao X F, Xu Y H, Li Z P, Wang L, Gao F M, Xiao D B. Elastic properties of novel rhenium nitrides from first principles [J]. Phys Status Solidi B, 2011, 248 (6): 2107-2111.
[20] Miao N H, Sa B S, Zhou J, Suna Z M, Ahuja R. Mechanical properties and electronic structure of the incompressible rhenium carbides and nitrides: A first-principles study [J]. Solid State Commun, 2011, 151(23): 1842-1845.
[21] Liang Y C, Yuan X, Zhang W Q. Ultrastiffness and metallicity of rhenium nitrides [J]. Appl Phys Lett, 2011, 109 (5): 053501.
[22] Soto G, Tiznado H, Reyes A, de la Cruz W. First principles calculations of interstitial and lamellar rhenium nitrides [J]. J Alloy Compd, 2012, 514: 127-134.
[23] Segall M D, Lindan P J D, Probert M J, Pickard C J, Hasnip P J, Clark S J, Payne M C. First-principles simulation: ideas, illustrations and the CASTEP code [J]. J Phys: Condens Matter, 2002, 14: 2717-2744.
[24] Vanderbilt D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism [J]. Phys Rev B, 1990, 41(11): 7892-7895.
[25] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple [J]. Phys Rev Lett, 1996, 77(18): 3865-3868.
[26] Thomas H F, Almlof J. General methods for geometry and wave function optimization [J]. J Phys Chem, 1992, 96(24): 9768-9774.
[27] Monkhorst H J, Pack J D. Special points for Brillouin-zone integrations [J]. Phys Rev B, 1976, 13(12): 5188-5192.
[28] Blanco M A, Francisco E, Luana V. GIBBS: Isothermal-isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model [J]. Comput Phys Commun, 2004, 158 (1): 57-72.
[29] Nye J F. Physical properties of crystals: Their representation by tensors and matrices [M]. New York: Oxford University Press, 1985.
[30] WU Z J, ZHAO E J, XIANG H P, HAO X F, LIU X J, MENG J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles [J]. Phys Rev B, 2007, 76(5): 054115.
[31] Zhang J D, YU Z D, CHENG X L, LI D H. Theoretical investigations of elastic and thermodynamic properties of hexagonal Re3N [J]. Comput Mater Sci, 2012, 62: 12-16.
[32] Panda K B, Ravi Chandran K S. Determination of elastic constants of titanium diboride (TiB2) from first principles using FLAPW implementation of the density functional theory [J]. Comput Mater Sci, 2006, 35(2): 134-150.
[33] He Y, Schwarz R B, Migliori A. Elastic constants of single crystal γ-TiAl [J]. J Mater Res, 1995, 10(5): 1187-1195.
[34] FU H Z, LIU W F, PENG F, GAO T. Theoretical investigations of structural, elastic and thermodynamic properties for PtN2 under high pressure [J]. Physica B: Conden Matter, 2009, 404(1): 41-46.
[35] PENG F, FU H Z, YANG X D. Ab initio study of phase transition and thermodynamic properties of PtN [J]. Physica B: Conden Matter, 2008, 403(17): 2851-2855.
张美光1,闫海燕2,魏 群3,黄多辉4
1. 宝鸡文理学院 物理与信息技术系,宝鸡 721016;
2. 宝鸡文理学院 化学化工学院,宝鸡 721013;
3. 西安电子科技大学 物理与光电工程学院,西安 710071;
4. 宜宾学院 四川省计算物理重点实验室,宜宾 644007
摘 要:采用基于密度泛函理论的第一性原理计算方法,系统研究高压高温下Re2N的晶体参数、力学性能和热力学性能。结果表明:在高压下Re2N具有明显的弹性各向异性,与弹性常数 C12、 C13、C44相比,C11和C33的变化随着压力的变化非常明显。此外,首次计算Re2N的体弹模量B、弹性模量E和剪切模量G沿不同晶轴的分布。弹性模量在一些主要晶轴方向上的大小分布趋势如下: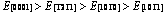 。计算结果还表明:在(0001)晶面,Re2N的抗剪切能力是最低的,从而极大地减小对大剪切变形的阻力。基于准简谐德拜模型,在0~50 GPa压力和0~1600 K温度下得到德拜温度、格林艾森参数、热传导以及热扩散系数的变化行为。
。计算结果还表明:在(0001)晶面,Re2N的抗剪切能力是最低的,从而极大地减小对大剪切变形的阻力。基于准简谐德拜模型,在0~50 GPa压力和0~1600 K温度下得到德拜温度、格林艾森参数、热传导以及热扩散系数的变化行为。
关键词:Re2N;过渡金属氮化物;弹性性能;热力学性能
(Edited by Chao WANG)
Foundation item: Project (11204007) supported by the National Natural Science Foundation of China; Project (2012JQ1005) supported by Natural Science Basic Research Plan of Shaanxi Province, China; Project (2013JK0638) supported by the Education Committee Natural Science Foundation of Shaanxi Province, China
Corresponding author: Mei-guang ZHANG; Tel: +86-917-3364258; E-mail: zhmgbj@126.com
DOI: 10.1016/S1003-6326(13)62921-0

