Trans. Nonferrous Met. Soc. China 22(2012) 686-693

Thermodynamics and kinetics of adsorption of molybdenum blue with

D301 ion exchange resin

ZHAO Zhong-wei^{1, 2}, XU Xiao-yang^{1, 2}, CHEN Xing-yu¹,

HUO Guang-sheng¹, CHEN Ai-liang¹, LIU Xu-heng², XU Hui³

1. School of Metallurgical Science and Engineering, Central South University, Changsha 410083, China;

2. Hunan Key Laboratory for Metallurgy and Material Processing of Rare Metals,Changsha 410083, China;

3. School of Physical Science and Technology, Central South University, Changsha 410083, China

Received 21 January 2011; accepted 2 June 2011

Abstract: The adsorption behavior of D301 for molybdenum blue was investigated. The thermodynamics parameters in adsorption process were calculated and the adsorption kinetics was studied. The experimental results show that the adsorption characteristic of D301 for molybdenum blue fits well with the Freundlich adsorption isotherm equation. In the adsorption process of D301 for molybdenum blue, both the enthalpy change ΔH and entropy change ΔS are positive, while the free energy change ΔG is negative when temperatures are in the range of 303-333 K. It is indicated that the adsorption is a spontaneous and endothermic process, and the elevated temperatures benefit to the adsorption. Kinetic studies show that the kinetic data are well described by double driving-force model, and the adsorption rate of molybdenum blue on D301 is controlled by the intraparticle diffusion during the adsorption process. The total kinetic equation is determined.

Key words: Ni-Mo ore; molybdenum blue; adsorption; thermodynamics; kinetics

1 Introduction

In South China, there are abundant lower cambrian black shales (Ni-Mo ores) which are rich in Ni, Mo, V, Cu, Co, Pb, Zn, P, Ti and so on [1,2]. In the Ni-Mo ores, jordisite, as the main molybdenum components, is an amorphous molybdenum sulfide (MoS_x) [3,4]. It is difficult to enrich the useful components in this Ni-Mo ore effectively by using the traditional physical and chemical processing technology due to its complex composition [5].

Currently, the treatment process of Ni-Mo ore has been researched, and several metallurgical processes have been proposed to prepare ammonium molybdate from the Ni-Mo ore. Generally, the Ni-Mo ore is leached by oxidation roasting-leaching or direct oxidation leaching in acidic or basic solution, and then the leaching solution was treated by ion exchange or solvent extraction [6, 7]. However, roasting will produce some byproducts, such as SO₂ and As₂O₃, which are harmful to environment. Additionally, the direct oxidation leaching also requires high-pressure equipments and high cost. Presently, a new progress, leaching molybdenum from Ni-Mo ore in alkali  solution by air oxidation, was proposed by our research group [8]. In this new technology, air is used as oxidant and a high leaching ratio can be obtained, and sulfur is oxidized and enters into the leaching solution in the forms of SO₄^2-, S₂O₃^2- and SO₃^2-, which avoids the emission of SO₂.

In the alkaline solution, the total concentration of SO₄^2-, S₂O₃^2-, SO₃^2-, SiO₄^3-, PO₄^3- and AsO₄^3- is much higher than that of MoO₄^2-. So, Mo is hard to extract by strong basic extractant or resin. Generally, the leaching solution is adjusted to weak acid, and the weak basic extractant or resin is used to extract Mo. In acidified solution, molybdates would be polymerized to polyions ([Mo₇O₂₄]^6-, [Mo₈O₂₆]^4-, etc) or react with impurity ions, such as AsO₄^2-, PO₄^3-, etc, to form heteropoly acid group anion ([XMo₁₂O₄₀]^3-(X: P, As, etc)) [9,10]. Because S₂O₃^2- and SO₃^2- ions coexist in the solution, part of Mo(VI) will be reduced into Mo(V) to form molybdenum blue [11]. Molybdenum blue is a macromolecule polyion and its size can reach nanometer scale [11-14]. Owning big size and high charge, molybdenum blue has a strong affinity with extractant or adsorbent. Our previous studies indicated that weak base extractant has a high efficiency, but the flammability, explosibility and fugitiveness of organic extractant cause bad operating environment, and generally the third phase will appear in the extracting process. Ion exchange process can avoid these drawbacks. In the former research, D314 resin was used to extract molybdenum at pH 2.5 in a column. Unfortunately, the results indicated that only at a very low feeding rate, a relatively high adsorption ratio could be obtained, therefore, the work efficiency is extremely low. However, at a high feeding rate, the breakthrough will occur soon. This is because the macromolecule polyion diffuses very slowly within the resin. In fact, the static ion exchange adsorption process can be used to extract the main ion when the affinity of resin to the main ion is much stronger than that to other ions. By the static ion exchange adsorption process, the resin can always contact with molybdenum blue ions. During the process of ion diffusion within resin, the adsorption can also occur simultaneously. After a period of time the molybdenum blue may be adsorbed completely. After being exchanged, the solution can be directly discharged to waste water treatment since it almost contains no Mo. So, the static ion exchange adsorption process is more suitable for the extraction of Mo.

As a familiar macroporous weak basic anion exchange resin, D301 has a high exchange capacity and good mechanical property. And the macroporous structure of D301 is beneficial for macromolecule polyion to diffuse and helpful to adsorbing the polyion of Mo in acidic condition solution. Hence, the thermodynamics and kinetics of D301 resin adsorbing molybdenum blue in static ion exchange adsorption process are studied in this work.

2 Experimental

2.1 Materials and feed solution preparation

In this study, molybdenum was leached by atmospheric leaching from Ni-Mo ore (collected from Guizhou Province of China) in alkali solution by air oxidation. In the leaching solution, molybdenum existed in the form of MoO₄^2- and coexisted with other anions such as SO₄^2-, S₂O₃^2-, SO₃^2-, SiO₄^2-, PO₄^3-, AsO₄^3-, SeO₃^2-, OH^-. The pH value of leaching solution was over 13. In order to extract molybdate, the leaching solution was treated as follows. Firstly, the pH value of leaching solution was adjusted to 8.0 by adding sulfuric acid, then the silica gel precipitate was filtered; lastly the pH value of the mother liquid was adjusted to 3.0 by adding sulfuric acid.

The D301 weak base anion exchange resin was provided by the Chemical Plant of Nankai University, China. The functional group of D301 resin is tertiary amine and the capacity of dry resin is ≥4.8 mmol/g. Standard solution of Mo(VI) was prepared from Mo₂O₃ (99.99%, provided by the Nanjing Chemical Reagent Company, China); the other reagents used were all of AR grade.

2.2 Experimental methods

2.2.1 Resin pretreatment

The resin was firstly dipped into the deionized water for 24 h, then pretreated with 4% HCl solution and 5% NaOH solution, respectively. Then 4% HCl solution was used to transform the resin into Cl-type. Finally, it was washed with deionized water adequately. The pretreated resin was dried in a vacuum drying chamber for 12 h, and was screened to obtain the particle with size of (0.35±0.03) mm. The pretreated resin was stored in the deionized water.

2.2.2 Adsorption and analytical method

A desired volume of feed solution was added into a three-necked flask, then the flask was placed in a thermostat water bath cauldron with stirrer. When the temperature reached the designed value, pH value was adjusted and then the desired mass of pretreated resin was added into the flask.

In the thermodynamics equilibrium experiment, adsorption of Mo lasted for 7 h to ensure that the adsorption reached equilibrium. The upper solution was taken for analysis after the adsorption equilibrium reached. Molybdenum in the solution was analyzed on a TU-1810 UV-vis spectrophotometer (Beijing Purkinje General Instrument Co., Ltd, China) at 460 nm. The equilibrium adsorption capacity Q_e (mg/g) was calculated by:

Q_e=V·(ρ₀-ρ_e)/m                               (1)

where V is the volume of solution, L; ρ₀ is the initial concentration of Mo in solution; ρ_e is the equilibrium concentration of Mo in solution, mg/L; m is the mass of dry resin, g.

In kinetics experiment, the resin was adsorbed for the desired time, and then was separated from the solution. The adsorbed resin was eluted with 5% NaOH solution for 3 h after being washed by deionized water 3-5 times. Then molybdenum in the desorption solution was analyzed by UV-vis spectrophotometer. The adsorption amount Q_t in a certain time was calculated as:

Q_t=V_t·ρ/m                                   (2)

E=Q_t/Q_e′×100%                              (3)

where ρ is the concentration of Mo in the aqueous, mg/L; V_t is the volume of desorption aqueous, L; m is the mass of dry resin, g; E is adsorption ratio, %; Q_e is the equilibrium adsorption capacity, mg/g.

3 Result and discussion

3.1 Adsorption thermodynamics

3.1.1 Effect of pH on adsorption capacity

The effect of pH value on the adsorption behavior of molybdenum blue with D301 resin is shown in Fig. 1.

Fig. 1 Effect of pH value on adsorption of molybdenum blue (Initial total concentration of Mo 5.89 g/L, 333 K, total volume of solution 300 mL)

As shown in Fig. 1 the adsorption of Mo decreases with the decrease of solution pH value from 4.2 to 2.1. This is because when the pH value of solution decreases, the amount of cation (such as MoO₂²⁺, MoO₂(OH)⁺) will increase, while D301 cannot exchange with this cations, hence the adsorption capacity will decrease. When pH>4.2, as the pH value of solution increases, polyanion will be depolymerized as MoO₄^2-. Since the affinity of D301 resin to polyanion is better than that to MoO₄^2-, the adsorption capacity of resin will be reduced accordingly. Thus, the optimal pH value should be 3.5-4.5. In the next study of thermodynamics adsorption, the pH value of solution was set at 4.0.

3.1.2 Adsorption isotherm

The adsorption isotherms were obtained under the following conditions: at each temperature of 303, 318 and 333 K, 0.5 g (dry mass) D301 resin was separately added into the solution with pH 4.0 for adsorption, whose initial concentrations of Mo were 0.2512, 0.4429, 0.751, 0.886, 1.030, 1.304 and 1.260 g/L, respectively. The adsorption isotherms are shown in Fig. 2.

Figure 2 shows that the equilibrium adsorption capacity will increase with the increase of temperature, indicating that higher temperature is favorable to     the adsorption process. The equilibrium adsorption  capacity will increase with the increase of equilibrium concentration. Langmuir and Freundlich models were used to evaluate the test data and to interpret the possible adsorption mechanism.

Fig. 2 Equilibrium adsorption isotherms of Mo on D301 resin at different temperatures

The Langmuir isotherm model assumes that homogeneous monolayer surface adsorption occurs and can be written as [15]:

                             (4)

where Q_e is the equilibrium adsorption capacity, mg/g; ρ_e is the equilibrium concentration of Mo in solution, mg/L; Q_m is the maximum adsorption capacity of the adsorbent, mg/g; b is the Langmuir constant, L/mg.

The Freundlich isotherm model assumes a heterogeneous and patch-wise surface that is independent from one another. The predigestion equation is as follows [16]:

                         (5)

where K_F and n are the constants of Freundlich isothermal equation.

The fitting results are shown in Fig. 3, and the corresponding equations are listed in Tables 1 and 2.

Table 1 Correlated parameters by Freundlich isotherm model

Table 2 Correlated parameters by Langmuir isotherm model

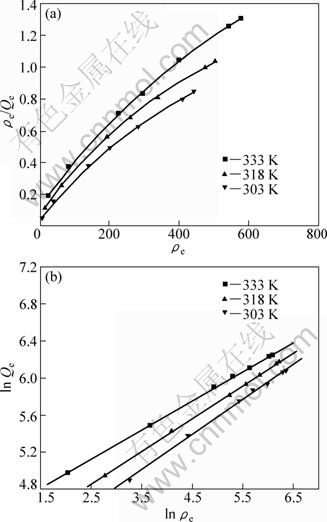
Fig. 3 Adsorption isotherms for molybdenum blue to D301 resin at different temperatures: (a) Freundlich isotherms; (b) Langmuir isotherms

From Tables 1 and 2 it can be seen that both Langmuir model and Freundlich model fit well the results with the R² values greater than 0.99. The fitted line by Langmuir model with a high correlation coefficient may originate from the formation of a thin film on the surface of the D301 resin due to the adsorption of molybdenum blues. However, the Langmuir equation is based on the assumption on homogeneous adsorbent surface, while on the surface of macroporous D301 resin, there are so much voids which are inhomogeneous. So, it is not reasonable to use the Langmuir model to describe the adsorption phenomena. In addition, the obtained maximum adsorption capacities (Q) at different temperatures (333, 318, 303 K) are 649.8, 551.2, 512.3 mg/g, respectively, while the fitted values of Q_m from the Langmuir model are smaller than those of Q at corresponding temperature. Therefore, the Freundlich model can fit the isothermal adsorption better.

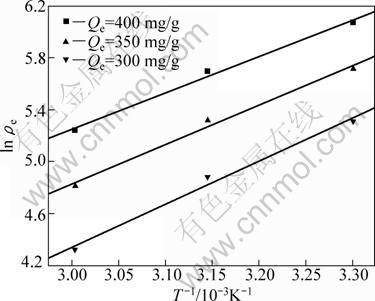
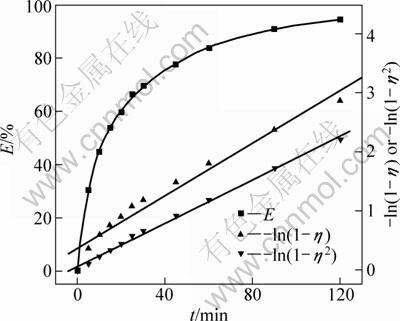
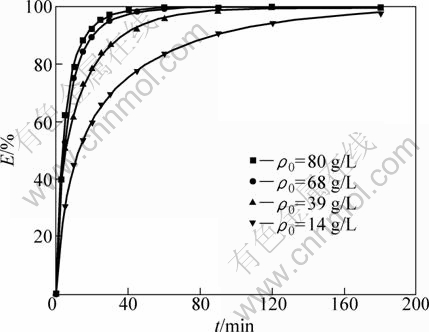
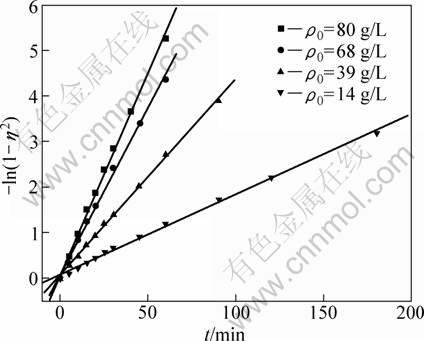
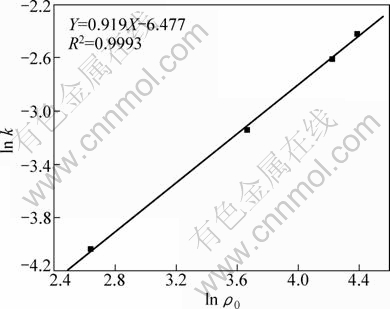
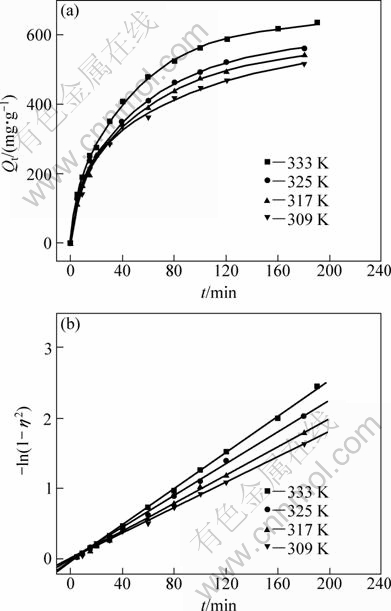
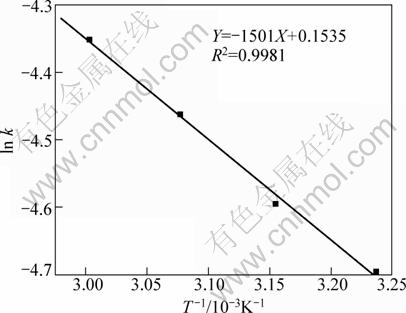
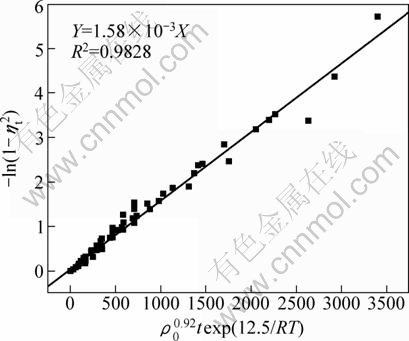
As shown in Table 1, the value n>1 represents the favorable adsorption condition. In most cases, the exponent 1

3.1.3 Thermodynamics

The thermodynamic behavior of Mo adsorption on D301 was evaluated using the following equations [17, 18]:

ΔG=-nRT                                   (6)

ΔS=(ΔH-ΔG)/T                              (7)

where n is the coefficient of the Freundlich isothermal equation; R is the gas constant; ρ_e is the equilibrium concentration under given adsorption capacity; T is the absolute temperature (K); ΔH is the change of enthalpy; ΔS is the change of entropy; ΔG is the change of Gibbs free energy. ΔH can be obtained by the following equation.

                           (8)

where K₀ is a constant.

The change of the enthalpy (ΔH) was determined from the slope of the linearized curves fitted with Eq. (8). (Fig. 4). At 303, 318 and 333 K, the adsorption thermodynamics parameters of Mo on D301 resin are shown in Table 3.

Fig. 4 Curve of ln ρ_e vs 1/T according to Eq. (8)

From Table 3 it can be seen that the calculated Gibbs free energy ΔG decreases as the reaction temperature is elevated at a fixed equilibrium adsorption capacity. Moreover, the calculated ΔG is negative, indicating that the adsorption process is spontaneous at the temperature ranging from 303 K to 333 K. All ΔH values are positive, showing the adsorption process is an endothermic reaction, and higher temperature avails the adsorption process. The change of entropy ΔS is positive, demonstrating that the adsorption process is an entropy increasing process. Generally, the adsorbate molecules often lose some degree of freedom (including translation and rotation) when being adsorbed to the solid phase from the liquid, and this is an process of entropy reduction. Nevertheless, the ion exchange reaction can desorb H₂O, which is an entropy increasing process. The total entropy change of the adsorption process (ΔS) is the sum of the above entropy increase and the entropy reduction. The final ΔS is positive.

Table 3 Thermodynamics parameters of adsorption

3.2 Adsorption kinetics

In order to investigate the rate law of Mo adsorption with D301 resin, the kinetic data were analyzed using two kinetic equations, i.e., the Boye liquid film diffusion model and intraparticle diffusion model.

The equation for the Boye liquid film diffusion model is

-ln(1-η_t)=k₁t                                (9)

where η_t=Q_t/Q_e, and Q_t and Q_e are the adsorption amounts at adsorption time t and at equilibrium, respectively.

The equation for the intraparticle diffusion model is [19-21]:

                 (10)

where D is an average intra-diffusion coefficient; r is the radius of the resin particle, [W]_e denotes the concentration of Mo in the resin at equilibrium; [W]_t is the concentration of Mo in the resin at time t. [W]_t values can be calculated by using the following equation:

[W]_t=V_t·C_t/m                                (11)

where V_t was the volume of desorption solution, C_t is the measured concentration in the desorption solution at time t, g/L; m is the mass of dry resin, g. When [W]₀=0 and [W]_t is a constant, integrating the above equations yields,

             (12)

Based on the equation η_t=[W]_t/[W] _e and Eq. (12), the integral of the model could be simplified as:

                            (13)

where η_t is the adsorption ratio, and k₂ (k₂=Dπ²/r²) is the apparent adsorption rate constant.

3.2.1 Judgment of rate control step

The rate control step experiments were conducted as follows: at 333K, 0.5 g (dry mass) D301 resin was placed into 14 g/L Mo solution at pH 4.0. The experimental results and the fitting results are shown in Fig. 5.

Fig. 5 Correlation of different models

Figure 5 shows that double driving-force model has a higher correlation coefficient (R²=0.9981) compared to Boye model (R²=0.9865). And we can see that Boye model seems more like a curve instead of a line. Therefore, the adsorption of molybdenum blue with D301 resin is more suitable to be described by double driving-force model, and this adsorption is an intraparticle diffusion controlled.

3.2.2 Effect of initial Mo concentration

The effect of concentration experiments are conducted as follows. At 333 K, 0.5 g (dry mass) D301 resin was separately placed into the solution at pH 4.0, whose concentration was 80, 68, 39 or 14 g/L. The results are shown in Fig. 6.

The curves show that the adsorption ratio E appears to be higher when the initial Mo concentration is greater during the adsorption process. Equilibrium time becomes shorter in higher concentration solution than in low concentration. It means that the higher the concentration is, the sooner the adsorption equilibrium reaches.

Fig. 6 Effect of initial Mo concentration on adsorption

The experimental data are fitted by the double driving-force model. The fitted results are shown in   Fig. 7, where the linear slope denotes the apparent adsorption rate constant k. As shown in Fig. 7, the fitted straight lines have high linear correlation, which further indicates that the adsorption is intraparticle diffusion controlled. And the adsorption rate constants increase with the increase of initial Mo concentration in the solution, which means higher concentration leads to a higher adsorption rate.

Fig. 7 Correlation of intraparticle diffusion model

The relationship between the apparent adsorption rate constant k and the solution concentration is fitted by ln k=b+cln ρ₀ (c is the reaction order in the exchange process, and b is a constant), and the fitted result is shown in Fig. 8. Thus, the reaction order of ion exchange in molybdenum solutions is about 0.92.

Fig. 8 Fitting curves of ln ρ₀ vs ln k

3.2.3 Effect of adsorption temperature

The effects of adsorption temperature experiments were conducted as follows. At temperatures of 309, 317, 325, and 333 K, 0.1 g (dry mass) D301 resin was placed into 6 g/L Mo solution at pH 4.0. The experimental and the fitted results are shown in Fig. 9.

Fig. 9 Effect of adsorption temperature: (a) t vs Q_t; (b) Correlation of intraparticle model

The curves show that the reaction rate increases obviously as the temperature elevates. It indicates that the adsorption is an endothermic process, and the elevated temperature is propitious to improve the reaction rate. The fitted straight lines have high linear correlation, which also further indicates that the adsorption is intraparticle diffusion controlled. The adsorption rate constant of D301 for Mo can be induced from the slope of the straight line which are shown in Table 4.

Table 4 Predicted kinetic constants for Mo adsorption on D301

Temperature/K

T^-1/10^-3K^-1

k

R²

ln k

333

3.003

12.89×10^-3

0.9996

-4.3513

325

3.077

11.54×10^-3

0.9990

-4.4619

317

3.155

10.1×10^-3

0.9994

-4.5952

309

3.236

9.13×10^-3

0.9988

-4.6962

Based on the data in Table 4, the plot of ln k versus 1/T is presented in Fig. 10. By fitting the data, the slope of the straight line is 1501, and the correlation coefficient R is 0.9981. According to the formula of Arrhenius equation ln k=-E_a/RT+ln A, the apparent activation  energy E_a is calculated to be 12.5 kJ/mol. It is clear that the adsorption reaction belongs to intraparticle diffusion.

Fig. 10 Determination of adsorption apparent activation energy

3.2.4 Total kinetics equation

Based on the experimental studies about the influences of initial molybdenum concentration and temperature, it can be concluded that the Double Driving-Force Model can be used to describe the ion exchange process in molybdenum solutions. The model can be described as: k=B₀ρ₀^0.92exp[12.5×10³/(RT)], where B₀ is a constant. The constant B₀ can be obtained by linear regression from the experimental data in Fig. 11 according to Eq. (13).

Fig. 11 Determination of constant B₀

Thus, the total kinetics equation of ion exchange process can be determined. The equation can be formulated as:

-ln(1-η_t²)=1.58×10^-3ρ₀^0.92texp[12.5× 10³/(RT)].

4 Conclusions

The results of the adsorption experiment show that Mo can be optimally adsorbed on D301 resin from the molybdenum feed solution at pH=3.5-4.5. The thermodynamic study indicates that the adsorption behavior of D301 resin for Mo well obeys the Freundlich isotherm and n value lies between 2 and 10, which demonstrates that Mo is easy to be adsorbed with D301 resin. And the adsorption process is spontaneous and endothermic and the system disorder increases in the duration. Kinetic studies show that the Mo adsorption follows the intraparticle diffusion model, and the activation energy E_a is 12.5 kJ/mol. And the total kinetic equation is determined as -ln(1-η_t²)=1.58×10^-3ρ₀^0.92t exp[12.5×10³/(RT)].

References

[1] FAN De-lian, YANG Xiu-zhen, WANG Lian-fang, CHEN Nan-sheng. Petrological and geochemical characteristics of a nickel- molybdenum-multi-element-bearing lower cambrian black shale from a certain district in south China [J]. Geochimica, 1973, 3: 143-163.

[2] KRIBEK B, SYKOROVA I, PASAVA J, MACHOVIC V. Organic geochemistry and petrology of barren and Mo-Ni-PGE mineralized marine black shales of the lower cambrian niutitang formation (southern China) [J]. International Journal of Coal Geology, 2007, 72(3-4): 240-256.

[3] PI Guan-hua, XU Hui, CHEN Bai-zhen, SHI Xi-chang, LI Jun-li. Study on recovering molybdenum from rocky-select Ni-Mo ores [J]. Hunan Nonferrous Metals, 2006, 23(1): 9-12. ( in Chinese).

[4] ZHAO Zhong-wei, ZHANG Gang, HUO Guang-sheng, LI Hong-gui. Kinetics of atmospheric leaching molybdenum from metalliferous black shales by air oxidation in alkali solution [J]. Hydrometallurgy, 2009, 97: 233-236.

[5] ZHU Jun, WANG Yan-jun, LI Ying-sheng. Experimental study on leaching of high carbon nickel molybdenum ore [J]. Mining and Metallurgical Engineering, 2009, 29(2): 75-78. (in Chinese)

[6] WU Hong-bei, FENG Guang-fen. Treatment of Ni-Mo ore by the method of acid curing leaching and solvent extraction: China, 1033784A [P]. 1989-07-12. (in Chinese)

[7] LI Qing-gang, XIAO Lian-sheng, ZHANG Gui-qing, ZHANG Qi-xiu. Process and practice of ammonium molybdate production from Ni-Mo ore by hydrometallurgy [J]. Chinese Journal of Rare Metals, 2007, 23(1): 9-12. (in Chinese)

[8] ZHANG Gang, ZHAO Zhong-wei, HUO Guang-sheng, CAO Cai-fang, LI Jiang-tao, CHEN Ai-liang, LI Hong-gui. The latest development of the treatment technology for Ni-Mo ores [J]. Chineses Journal of Rare Metal and Cemented Carbides, 2008, 36(4): 37-41. (in Chinese)

[9] TYTKO K H, BAETHE G, CRUYWAGEN J J. Equilibrium studies of aqueous polymolybdate solutions in 1 M NaCl medium at 25 °C [J]. Inorg Chem, 1985, 24: 3132-3136.

[10] CRUYWAGEN J J, DRAAIJER A G, HEYNS J B B, ROHWER E A. Molybdenum (VI) equilibria in different ionic media formation constants and thermodynamic quantities [J]. Inorganica Chimica Acta, 2002, 331: 322-329.

[11] MULLER A, SERAIN C. Soluble molybdenum bluess“des pudels kern” [J]. Accounts of Chemical Research, 2000, 33: 2-10.

[12] JIA Xiang-feng, FAN Da-wei, TANG Pei-qin, HAO Jing-cheng, MA Li-ying, LIU Tian-bo. “Second organized structures”of nanoscale inorganic polyoxomolybdate compound [J]. Acta Phys Chim Sin, 2006, 22(10): 1300-1304. (in Chinese)

[13] MULLER A, KRICKEMEYER E, BOGGE H, B?GGE H, SCHMIDTMANN M, BEUGHOLT C, KOGERLER P, LU C Z. Formation of a ring-shaped reduced “metal oxide” with the simple composition [(MoO₃)₁₇₆(H₂O)₈₀H₃₂] [J]. Angew Chem Int Ed Engl, 1998, 37: 1220-1223.

[14] M?LLER A, KRICKEMEYER E, MEYER J, BOGGE H. [Mo₁₅₄(NO)₁₄O₄₂₀(OH)₂₈(H₂O)₇₀]^(25±5)-: A water-soluble big wheel with more than 700 atoms and a relative molecular mass of about 24 000 [J]. Angew Chem Int Ed Engl, 1995, 34: 2122-2124.

[15] DO D D. Adsorption analysis: Equilibrium and kinetics [M]. London: Imperial College Press, 1998.

[16] XIONG Chun-hua, YAO Cai-ping. Study on the adsorption of cadmium(II) from aqueous solution by D152 resin [J]. Journal of Hazardous Materials, 2009, 166: 815-820.

[17] GARCLA-DELGADO R A, COTOUELO-MINGUEZ L M, RODFIHUEZ J J. Equilibrium study of single-solute adsorption of anionic surfactants with polymeric XAD resins [J]. Separation Science and Technology, 1992, 27(7): 975-987.

[18] JUANG R S, SHIAU J Y, SHAO H J. Effect of temperature on equilibrium adsorption of phenols onto nonionic polymeric resins [J]. Separation Science and Technology, 1999, 34(9): 1819-1831.

[19] FLEMING C A, NICOL M J. A comparative study of kinetic models for the extraction of uranium by strong-base anion-exchange resins [J]. Journal of the South African Institute of Mining and Metallurgy, 1980, 80(2): 89-99.

[20] VERMULEN T. Theory for irreversible and constant-pattern solid diffusion [J]. Ind Eng Chem, 1953, 45: 1664-1670.

[21] HAINES A K. The development of continuous fluidized-bed ion-exchange in South Africa and its use in the recovery of uranium [J]. Journal of the South African Institute of Mining and Metallurgy, 1978, 78(12): 303-315.

D301树脂吸附钼蓝的热力学与动力学

赵中伟^{1, 2}，许晓阳^{1, 2}，陈星宇¹，霍广生¹，陈爱良¹，刘旭恒²，徐 慧³

1. 中南大学 冶金科学与工程学院，长沙 410083；

2. 稀有金属冶金及材料制备湖南省重点实验室，长沙 410083；

3. 中南大学 物理科学与技术学院，长沙 410083

摘  要：通过静态吸附实验，研究D301树脂对钼蓝的吸附热力学和动力学。结果表明：D301对钼蓝的吸附行为符合Freundlich等温方程；在不同温度下，D301吸附钼蓝的吸附焓变ΔH和吸附熵变ΔS均为正值，而吸附自由能变ΔG为负值，表明吸附是一个自发的、吸热过程，升温有利于吸附。动力学研究表明，此吸附过程符合双驱动模型，吸附过程主要受粒内扩散步骤控制，经拟合获得动力学总方程。

关键词：镍钼矿；钼蓝；吸附；热力学；动力学

(Edited by YUAN Sai-qian)

Foundation item: Project (2007AA06Z129) supported by the High-tech Research and Development Program of China

Corresponding author: ZHAO Zhong-wei; Tel: +86-731-88830476; E-mail: zhongweizhao@hotmail.com

DOI: 10.1016/S1003-6326(11)61232-6