基于粒子滤波器的移动机器人惯导传感器故障诊断  

段琢华^1,2, 蔡自兴¹, 于金霞^1,3, 邹小兵¹

(1.中南大学 信息科学与工程学院,湖南 长沙,410083;

2.韶关学院 计算机科学系,广东 韶关,512003;

3.河南理工大学 计算机科学与技术系,河南 焦作,454000)

摘要: 提出一种粒子滤波器方法用于诊断移动机器人惯性导航系统传感器故障。该方法将基于规则的推理与多粒子滤波器结合,利用规则推理确定机器人运动状态,每一种运动状态用一个粒子滤波器监视。该方法有效地解决了单个粒子滤波器难以表示复杂逻辑的问题,降低了每个粒子滤波器的粒子数,从而提高了诊断效率和精度。对移动机器人在5种平面运动状态下(静止、直线运动、转动等)的8种工作模式(包括1种正常工作模式和7种故障模式)进行监视的仿真结果表明,采用所提出的方法可以有效地识别惯导系统的1个或多个硬故障。

关键词: 移动机器人; 故障检测; 故障诊断; 粒子滤波器

中图分类号:TP24 文献标识码:A 文章编号: 1672-7207(2005)04-0642-06

Particle filter-based fault diagnosis for inertial navigation system of mobile robot

DUAN Zhuo-hua^1,2, CAI Zi-xing¹, YU Jin-xia^1,3, ZOU Xiao-bing¹

(1.School of Information Science and Engineering, Central South University, Changsha 410083, China;

2.Department of Computer Science, Shaoguan University, Shaoguan 512003, China;

3.Department of Computer Science and Technology, Henan Polytechnic University, Jiaozuo 454000, China)

Abstract: A particle filter-based approach for fault diagnosis of inertial sensor of wheeled mobile robots was proposed, in which the rule-based inference and multiple particle filters were integrated. The rule-based inference method was employed to determine the movement states of the robot. Each movement state was monitored by a particle filter. This approach overcomes some shortcomings of particle filter such as weak logic inference capability, decreases particle number, increases efficiency and accuracy of each particle filter. The results of monitoring 8 kinds of operation mode of inertial navigation system (INS) of 5 kinds of movement states of mobile robot in a plane show that the approach presented can diagnose one or more hard faults of intertial navigation system sensors of mobile robots.

Key words: mobile robot; fault detection; fault diagnosis; particle filter

 

   故障诊断对于移动机器人的可靠性和安全性至关重要^[1]。国内外关于结构化或半结构化环境下移动机器人故障诊断研究较多,对内部惯导传感器故障诊断研究较为成熟,主要采用基于多模型的方法^[2-4]。在多模型方法中,每个故障模式的动力学模型用一个卡尔曼滤波器实现。由于系统故障数目随元件数目呈指数增长,导致计算复杂度呈指数增大;此外,采用卡尔曼滤波器的前提是系统噪声均值为  零且具有已知协方差的高斯过程。为了克服多模型方法存在的计算复杂度大以及高斯假设约束问题,许多学者开始研究基于粒子滤波器的故障诊断方法,如V.Verma等^[5-11]利用粒子滤波器监视混合状态空间,分析了该方法对于移动机器人故障诊断的可行性。经典粒子滤波器在应用于故障诊断时存在以下问题:

a. 对于低概率发生的故障状态,可能没有粒子进入故障状态;

b. 混合系统的高维状态空间要求更多的粒子数来近似后验分布,增加了计算复杂度^[5];

c. 粒子滤波器难以表示复杂的逻辑。

一些研究工作者对如何提高粒子滤波器的工作效率进行了研究。de Freitas^[8]提出了RBPF, RBPF只对离散状态进行采样,每个离散状态确定一个线性高斯状态空间模型;MO Yi-wei等^[9]提出改进的RBPF算法来处理问题a.。S. Thrun等^[10]利用风险敏感粒子滤波器(RSPF)解决问题a.,通过引入风险权值来加大小概率故障状态的权重,V.Verma等^[11]利用变分辨率粒子滤波器(VRPF)解决问题b.。

上述方法在一定程度上提高了粒子滤波器的效率,但都没有涉及问题c.。为此,本文作者采用基于规则推理与粒子滤波器相结合的方法,利用基于规则的推理方法确定机器人运动状态,不同的运动状态采用不同的粒子滤波器。

1 基于粒子滤波器的故障诊断方法

粒子滤波器是监视动态系统的蒙特卡罗(即随机选择)方法,通过带权样本(即粒子)集非参数化地近似概率分布。粒子滤波器为估计混合系统的状态提供了一种计算上可行的方法,除了具有计算上的优势外,在单个粒子滤波器中可以同时表示离散和连续状态,而且不受高斯假设的约束(可以表示任意分布)。

利用粒子滤波器实现故障诊断的主要方法是:设S是移动机器人离散故障和操作模式有限集合,s_t∈S是t时刻的状态,{s_t}表示状态随时间演化的离散一阶马尔可夫链。故障诊断就是提供每一时刻的信度p(关于状态集合S的后验概率分布),

其中:i∈S, j∈S。故障状态确定了系统的动态模型。设x_t表示系统在t时刻的多变量连续状态,非线性条件状态转移模型表示为p(x_t|s_t,x_t-1)。机器人的状态基于测量模型p(z_t|s_t,x_t)和测量序列{z_t}来观测。

故障诊断问题是估计后验分布p(s_t,x_t|z_1··t)的边缘分布p(s_t|z_1··t)。后验分布的递推估计可通过如下贝叶斯滤波器获得。

 

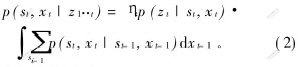
其中:η_t为标准化因子。

式(2)中的积分以及标准化因子难以计算。粒子滤波器通过N个完全实例化的状态样本(粒子)集合{〈s^[1]_t,x^[1]_t〉,…,〈s^[N]_t,x^[N]_t〉}及重要性权值{ω^[1]_t}来近似后验概率分布,即

 

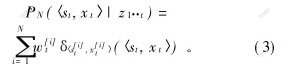
其中:δ(·)表示Dirac delta函数。当N→∞时,式(3)中的近似达到真实后验分布。由于不能从真实后验分布提取样本,采用从建议分布(或称重要性分布)q(·)提取样本。重要性权值用于处理建议分布q(·)和真实分布p(s_t,x_t|z_1··t)之间的差异,对于给定的样本〈s^[i]_t,x^[i]_t〉,其重要性权值为

 

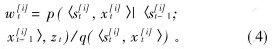
粒子滤波器的一种迭代算法如下。

算法1 故障诊断的粒子滤波器算法

 

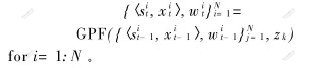
a. 采样

 

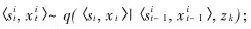
b. 更新权值

 

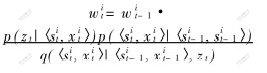
End for

c. 权值标准化

 

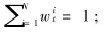
d. 状态估计

(1) 根据{〈sⁱ_t,xⁱ_t〉,wⁱ_t}^N_i=1计算边缘密度分布

 

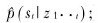
(2) 离散状态估计:s_t=s,使得

 

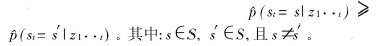
e. 若退化严重,则重新采样

 

 

2 系统及其模型

Z.X.Cai等^[12]设计并研制了适应复杂地形的移动机器人系统,如图1所示。该系统配置了2类传感器(内部传感器和外部传感器)。内部传感器包括编码器、陀螺仪、倾斜仪、旋转角传感器。其中,编码器用于测量轮子角速度;陀螺仪用于测量偏航率;倾斜仪用于测量俯仰角和横滚角;旋转角传感器用于测量摇臂夹角。该机器人具有一定的越障能力,能行走于较复杂的地形。在此,仅研究平面运动时的故障诊断问题。当机器人在平面运动时,其位姿通过编码器和陀螺仪感知,相应的运动学模型如图2以及下列方程所示。

 

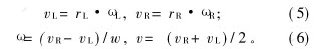
其中:r_L,r_R和w分别为左前轮半径、右前轮半径和轴长;ω_L和ω_R为编码器输出,分别表示左前轮和右前轮角速度;ω为陀螺仪输出,表示偏航率;图2中Φ为航向角;ω为Φ的导数。

 

图 1   待诊断的移动机器人

Fig. 1   Mobile robot to be diagnosed   

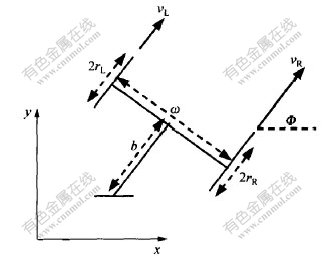
图 2   移动机器人运动学模型

Fig. 2   Kinematic model of mobile robot  

  状态向量x=[ω_L,ω_R,ω]^T;输入向量u=[u_L,u_R ]^T,观测向量z=[ω_L,ω_R,ω]^T。其中:u_L和u_R为控制输入,分别表示左轮和右轮设定速度。

p(x_t|x_t-1,s_t)用以下线性高斯模型表示:

x_t=A(s_t)x_t-1+B(s_t)w_t+F(s_t)u_t;

p(z_t|x_t,s_t)用以下线性高斯模型表示:

z_t=C(s_t)x_t+D(s_t)v_t+G(s_t)u_t。

其中:s_t∈S={S₀,S₁,S₂,S₃,S₄,S₅,S₆,S₇};S₀表示系统工作正常;S₁表示左轮编码器失效;S₂表示右轮编码器失效;S₃表示陀螺仪失效;S₄表示左、右轮编码器同时失效;S₅表示左轮编码器和陀螺仪同时失效;S₆表示右轮编码器和陀螺仪同时失效;S₇表示左、右轮编码器和陀螺仪同时失效。各状态的系统参数矩阵为:

 。

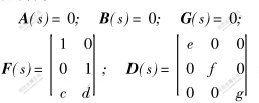其中:s∈S;c=-rL/w,d=rR/w;e=0.1;f=0.1;g=0.0223。e,f,g分别表示左、右轮编码器和陀螺仪噪声的标准差。

不同的故障模式的运动学模型的差异通过不同的观测方程表示,例如:

 

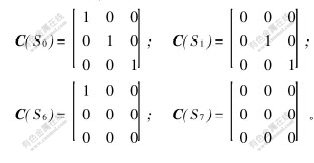
3 基于多粒子滤波器的故障诊断

在将粒子滤波器用于移动机器人故障诊断时,遇到了如下困难:移动机器人在不同运动状态下,诊断系统具有不同的诊断能力。例如,当机器人直线前进时,陀螺仪的输出近似为零,粒子滤波器方法有可能将此状态识别为陀螺仪故障。因此,在考虑移动机器人故障诊断时,除了要考虑离散故障状态和连续状态之外,还要考虑离散的运行状态。移动机器人可能处于不同的运动状态(静止、直线运动、转动等),每种运动状态又有多种工作模式(正常、编码器异常、陀螺仪异常等),每种工作模式对应不同的运动学模型。例如,在机器人静止时,无法诊断惯导传感器。对于直线运动状态,可以诊断左、右轮编码器的故障,但无法诊断陀螺仪的故障,因此,必须对不同的运动状态分别进行处理。

机器人运动状态的判定由左、右驱动轮的设定速度确定。考察5种运动状态m₀,m₁,m₂,m₃和m₄分别是静止、直线运动、转动1、转动2及转动3状态。它们的前提条件分别为:u_L=u_R=0;u_L=u_R≠0;u_L=0,u_R≠0;u_L≠0,u_R=0;u_L≠u_R,u_L≠0,u_R≠0。

针对上述同时具有两类离散状态和一类连续状态的系统,一种处理方法是将两类离散状态合并成一类离散状态,然后利用单个粒子滤波器的方法。这种处理方法导致2个问题:出现高维的状态空间;需在粒子滤波器内部处理部分判断逻辑。为此,本文作者采用多个粒子滤波器的方法,对不同的运动状态采用不同的粒子滤波器,在粒子滤波器外部利用基于规则的推理处理运动状态的判别。具体实现如下:

为m₁,m₂,m₃,m₄分别设计粒子滤波器PF1, PF2, PF3, PF4。PF1处理的故障状态为{S₀, S₁, S₂, S₄};PF2处理的故障状态为{S₀, S₂, S₃, S₆};PF3处理的故障状态为{S₀, S₁, S₃, S₅};PF4处理的故障状态为{S₀, S₁, S₂, S₃, S₄, S₅, S₆, S₇}。

不失一般性,4个粒子滤波器的各状态之间采用相同的转移概率。即PF1,PF2和PF3的离散状态转移概率设为P(s_t=i|s_t-1=j)=0.250,PF4的离散状态转移矩阵为P(s_t=i|s_t-1=j)=0.125。每个粒子滤波器采用算法1的结构。逻辑推理与多粒子滤波器相结合的算法伪码如下。

算法2 多粒子滤波器算法

PF1~PF4初始化

for t=1∶T,

if u_L(t)=u_R(t)≠0,应用PF1:

{〈sⁱ_t,xⁱ_t〉,wⁱ_t}^N_i=1=

PF1({〈sⁱ_t-1,xⁱ_t-1〉,wⁱ_t-1}^N_i=1,z_k);

if u_L(t)=0, u_R(t)≠0,应用PF2:

{〈sⁱ_t,xⁱ_t〉,wⁱ_t}^N_i=1=

PF2({〈sⁱ_t-1,xⁱ_t-1〉,wⁱ_t-1}^N_i=1,z_k);

if u_L(t)≠0, u_R(t)=0,应用PF3:

{〈sⁱ_t,xⁱ_t〉,wⁱ_t}^N_i=1=

PF3({〈sⁱ_t-1,xⁱ_t-1〉,wⁱ_t-1}^N_i=1,z_k);

if u_L(t)≠u_R(t), u_L(t)≠0, u_R(t)≠0,应用PF4:

{〈sⁱ_t,xⁱ_t〉,wⁱ_t}^N_i=1=

PF4({〈sⁱ_t-1,xⁱ_t-1〉,wⁱ_t-1}^N_i=1,z_k)

end for。

4 实验结果

实验平台为图1所示移动机器人,实验方案如图3所示,机器人运动状态:m₀→m₄→m₀→m₄→m₀→m1。粒子滤波器PF1,PF2,PF3和PF4利用Matlab实现,故障通过对实测数据设置为0来仿真。在粒子数设置为100时的实验结果如图4和5所示。实验结果表明,集成逻辑与多粒子滤波器的方法能有效地处理不同运动状态下的故障诊断,效率高,误诊率低。

图4所示为利用PF4对7.65~13.50 s时间段(m₄状态)的诊断仿真结果,处理时间为20 s。可见:在7.65~10.00 s时间段系统正常,在t=10.05 s处左轮编码器发生故障(S₁);在t=11.55 s处右轮编码器发生故障(S₄);在t=12.55 s处陀螺仪发生故障(S₇)。

图5所示为利用PF1对14.70~37.15 s时间段(m₁状态)的诊断仿真结果,处理时间为108 s。可见:在14.70~22.45 s时间段系统正常;在t=22.50 s时刻左轮编码器发生故障(S₁),在t=30.00 s时刻右轮编码器发生故障(S₄)。

  

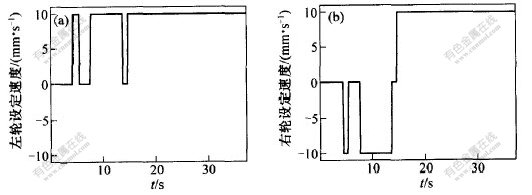
图 3   机器人左、右轮设定速度

Fig. 3   Designed velocity of left and right wheels of mobile robot  

 

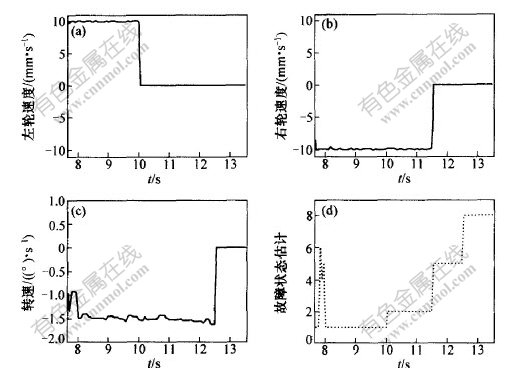
图 4   利用PF4的诊断仿真结果(误检数为3)

Fig. 4   Simulation results of diagnosing with PF4 (number of misdetection is 3)  

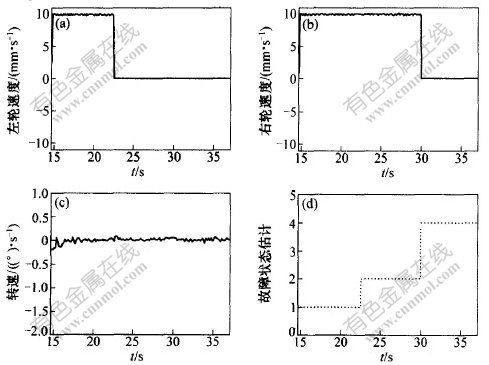
图 5   利用PF1的诊断仿真结果(误检数为0)

Fig. 5   Simulation results of diagnosing with PF1 (number of misdetection is 0)  

5 结 论

a. 提出一种基于多粒子滤波器的移动机器人惯导传感器故障诊断方法,诊断移动机器人在不同运动状态下左、右轮编码器和陀螺仪的单个或多个硬故障。

b. 针对粒子滤波器存在高维状态空间计算复杂度高以及难以表示复杂逻辑的问题,提出将基于规则的推理与多粒子滤波器相结合的方法,降低了每个粒子滤波器的维数,处理多种运动状态下的机器人故障诊断问题。

c. 仿真实验表明,所提出的方法能有效地提高每个粒子滤波器的效率,降低误诊率。

参考文献:

[1]蔡自兴,贺汉根,陈虹.未知环境中移动机器人导航控制研究的若干问题[J].控制与决策, 2002, 17(4): 385-390.

CAI Zi-xing, HE Han-gen, CHEN Hong. Some issues for mobile robot navigation under unknown environments[J]. Control and Decision, 2002, 17(4): 385-390.

[2]Roumeliotis S I, Sukhatme G S, Bekey G A. Sensor fault detection and identification in a mobile robot[A]. IEEE/RSJ Int’l Conf on Intelligent Robots and Systems[C]. Victoria, 1998.

[3]Goel P, Dedeoglu G, Roumeliotis S I, et al. Fault detection and identification in a mobile robot using multiple model estimation and neural network[A]. IEEE Int’l Conf on Robotics & Automation[C]. San Francisco, 2000.

[4]Hashimoto M, Kawashima H, Nakagami T, et al. Sensor fault detection and identification in dead-reckoning system of mobile robot: interacting multiple model approach[A]. Int’l Conf on Intelligent Robots and Systems[C]. Hawaii, 2001.

[5]Verma V, Gordon G, Simmons R, et al. Real-time fault diagnosis(robot fault diagnosis)[J]. IEEE Robotics & Automation Magazine, 2004, 11(2): 56-66.

[6]Verma V, Langford J, Simmons R. Non-parametric fault identification for space rovers[A]. International Symposium on Artificial Intelligence and Robotics in Space[C]. Montreal, 2001.

[7]Verma V, Gordon G, Simmons R. Efficient monitoring for planetary rovers[A]. International Symposium on Artificial Intelligence and Robotics in Space[C]. Nara, 2003.

[8]de Freitas N. Rao-blackwellised particle filtering for fault diagnosis[A]. Proceedings 2002 IEEE Aerospace Conference[C]. Big Sky, 2002.

[9]MO Yi-wei, XIAO De-yun. Hybrid system monitoring and diagnosing based on particle filter algorithm[J]. Acta Automatica Sinica, 2003, 29(5): 641-648.

[10]Thrun S, Langford L, Verma V. Risksensitive particle filters[A]. Proceedings of the Neural Information Processing Systems Conference[C]. Vancouver, 2002.

[11]Verma V, Thrun T, Simmons R. Variable resolution particle filter[A]. Proceedings of the International Joint Conference on Artificial Intelligence[C]. Acapulco, 2003.

[12]Cai Z X, Zou X B, Wang L, et al. A research on mobile robot navigation control in unknown environment: objectives, design and experiences[A]. Proceedings of Korea-Sino Symposium on Intelligent Systems[C]. Busan, 2004.

收稿日期:2005-03-01

基金项目:国家自然科学基金重点项目(60234030)

作者简介:段琢华(1969-),男,湖南冷水江人,博士研究生,讲师,从事移动机器人故障诊断研究

论文联系人: 段琢华,男,博士研究生;电话:0731-2655993(O);E-mail:duanzhuohua@163.com