文章编号：1004-0609(2016)-12-2488-11

应变速率对藕状多孔镁垂直于气孔方向压缩变形行为与力学性能的影响

刘新华，晏玉平，谢建新

(北京科技大学 新材料技术研究院，北京 100083)

摘  要：利用定向凝固法制备藕状多孔镁，采用GLEEBLE-1500型材料模拟实验机和分离式霍普金森压杆(SHPB)装置，在以1×10^-3~1650 s^-1的应变速率范围内沿垂直于气孔方向进行压缩实验，研究应变速率对藕状多孔镁压缩变形行为和力学性能的影响。结果表明：当垂直于气孔方向压缩时，藕状多孔镁的应力-应变曲线分为应力线性增加的弹性阶段、应力缓慢增加的平台阶段和应力急剧增加的密实化阶段，应力随应变的增加持续增大，无应力峰值的出现。而当垂直于气孔方向压缩时，应变速率对藕状多孔镁的变形行为影响显著，在应变速率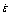<60 s^-1条件下，主要变形方式为气孔先发生椭圆化变形，然后部分气孔的孔壁率先向气孔内发生弯月形塌陷并形成垂直于压缩方向的先变形带，随后变形带不断产生，从而逐步实现密实化；而较高应变速率(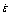=450~1650 s^-1)下的变形方式虽然气孔也是先后发生椭圆化、孔壁向气孔内的弯曲塌陷等变形并形成先变形带，但先变形带沿试样对角线方向率先形成，并随压缩进行不断向与对角线垂直的方向扩展。应变速率对藕状多孔镁的力学性能有较明显的影响，其影响机制主要是由于不同应变速率时气孔的变形方式发生了变化。

关键词：藕状多孔镁；应变速率；变形行为；力学性能；变形机制

中图分类号：TG146；TG115　　           文献标志码：A

多孔金属是一类新型的工程材料，与致密金属相比，具有密度低、恒定压缩应力下的变形大、表面积大、渗透性好等特殊性能，被广泛应用于轻质结构部件、热交换器、过滤器、吸声元件以及生物工程材料等领域^[1-3]。其中，低密度和独特的压缩应力响应特性，使多孔金属可作为理想的能量吸收和安全防护材料广泛用于交通工具、航空航天、军事装备等高技术领域。藕状多孔金属是近年发展起来的一种新型多孔金属^[4]，与泡沫金属相比，其孔隙结构不是圆球形或多边形气孔随机分布于金属基体中，而是圆柱形气孔沿同一方向规则分布于金属基体中，这一结构特点使其具有在沿气孔轴向加载时不存在明显的应力集中、较高的拉伸和压缩强度以及较高应力平台等优异的力学特性，因此，藕状多孔金属成为近年来多孔材料研究的热点^[5-9]。

镁具有密度低(1.74 g/cm³)、比强度高、减震性能好等优点，多孔镁材料可望兼具超轻和强吸能减震特性，在航空航天、汽车工业、高速交通等高技术领域具有重要应用前景。因此，高性能多孔镁的制备研究受到高度重视，开发出了泡沫镁等多孔镁材料^[10-13]。研究结果表明^[13]，泡沫镁具有较长的应力平台和优良的能量吸收性能。但由于泡沫镁不规则的孔隙结构特点，压缩时应力集中比较严重，力学性能较低。藕状多孔镁的孔隙结构具有取向分布的特点，这种规则结构的多孔金属在压缩时的变形行为和力学性能如何是值得研究的重要问题。

另一方面，在用作轻质结构和能量吸收部件时，多孔金属往往不只是发生静态变形，也常发生动态变形。把握多孔金属材料在较大应变速率范围载荷作用下的力学特性可为吸能结构和安全防护元件的材料选择和结构设计提供重要参考，因而受到研究人员高度关注，并在此方面进行了大量的研究工作^[14-18]。在前期研究中，本文作者研究发现，藕状多孔镁在压缩方向平行于气孔方向的条件下当应变速率较大时，应变速率对藕状多孔镁的变形行为和力学性能有较明显的影响^[19]。然而，藕状多孔金属的孔隙结构具有显著的各向异性，当压缩方向不同时，应变速率对藕状镁的变形行为是否产生明显影响，如何影响以及影响的机理如何尚需进一步研究。

在此，以藕状多孔镁为对象，在以1×10^-3~1650 s^-1的较大应变速率范围内，沿垂直于气孔方向进行压缩变形，研究了应变速率对藕状多孔镁压缩变形行为和力学性能的影响，探讨了其影响机理。

1  实验

1.1  实验材料

采用定向凝固法制备藕状多孔镁，所用装置如图1所示。实验时，先确保装置密封良好，避免气体泄露，然后对凝固装置抽真空，当真空度达到1.0 Pa后充入氢气，并使其压力达到约0.1 MPa。开启加热装置熔化金属，至760 ℃时保温0.5 h，使气体在金属液中充分溶解达到饱和。采用氧化铝陶瓷铸型，其内径50 mm，高170 mm。铸型在镁熔化后保温过程中进行预热，预热温度设定为500 ℃。达到设定温度时提起石墨塞棒，将金属液注入预热的铸型中进行定向凝固，获得藕状多孔镁棒材，形貌如图2所示。

采用电火花线切割将制备所得藕状多孔镁棒料加工成尺寸为15 mm×15 mm×15 mm的立方体试样，试样的4个侧面与气孔方向平行，两个端面与气孔方向垂直，切割时力求保证良好的平行度和垂直度。将切割后的立方体试样经超声波清洗，去除加工过程中残留其中的杂质。之后通过称量和计算体积的方法确定相对密度和孔隙率，分别按式(1)和式(2)进行计算。

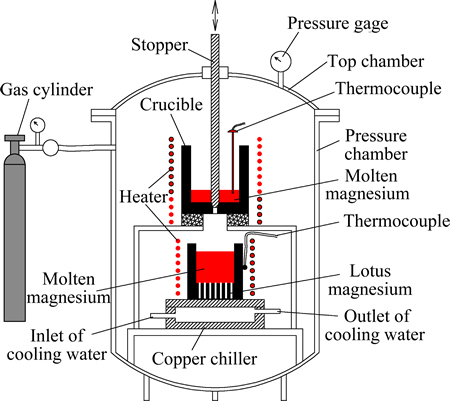
图1  藕状多孔金属定向凝固制备装置示意图

Fig. 1  Schematic diagram of unidirectional solidification processing for fabricating lotus-type porous metals

图2  藕状多孔镁棒料截面形貌

Fig. 2  Section morphologies of lotus-type porous magnesium bar

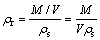                            (1)

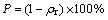                           (2)

式中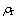：为相对密度；M为藕状多孔镁试样的质量， g；V为试样的名义体积，cm³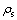；为致密纯镁的密度，取1.74 g/cm³；P为孔残率，%。

采用Image J软件对压缩试样的孔隙结构特征进行分析。可知，藕状多孔镁压缩试样的平均孔径为0.7~1.7 mm，孔隙率为45%~64%。

1.2  实验方法

选用孔隙比较均匀的藕状多孔镁试样，分别在低应变速率、中应变速率和高应变速率下对其进行压缩实验。所有压缩实验均保持压缩方向平行气孔方向，如图3所示。

1.2.1  较低应变速率时的压缩实验方法

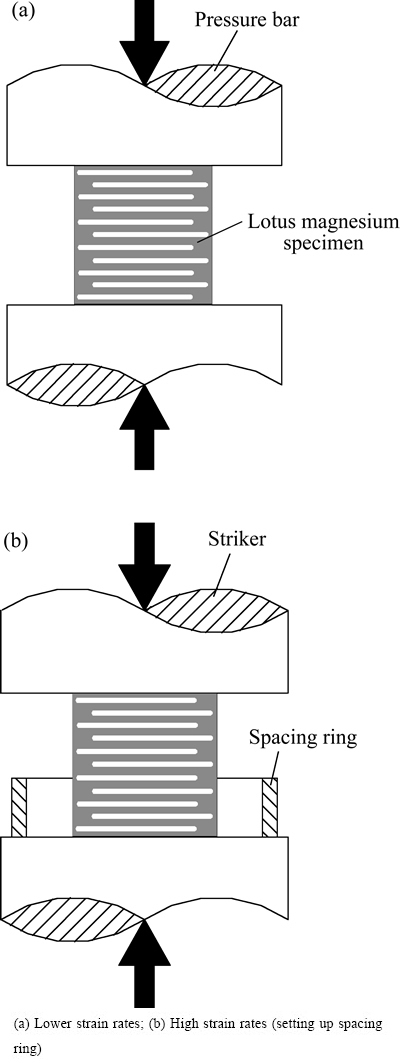
图3  压缩实验方法示意图

Fig. 3  Schematic diagrams of compression experiments

在室温下，采用GLEEBLE-1500型模拟实验机进行低和中应变率压缩实验，应变速率采用以0.001、0.1、1.0和30.0 s^-1，变形量控制在80%以上。实验获得载荷和位移数据，利用试样原始面积除载荷数据得到工程应力，利用原始高度除位移数据获得工程应变。

1.2.2  高应变速率时的压缩实验方法

分离式霍普金森压杆(Split Hopkinson pressure bar，SHPB) 是研究材料在高应变速率下的力学特性的重要方法。但多孔材料通常需要研究较宽的应变范围(弹性阶段、屈服阶段和密实阶段)，而分离式霍普金森压杆则无法实现如此大的应变范围，特别是对于强度较大、孔隙率较高的多孔金属材料更加困难。在分离式霍普金森压杆基础上发展的直接撞击式霍普金森压杆实验技术可以获得较大的应变范围^{[13, 19]}，其原理如图4所示。本研究中采用直接撞击式霍普金森压杆实验技术进行动态压缩实验，应变速率分别为450、950和1650 s^-1，获得的典型信号数据如图5所示，最大应变控制在0.8左右。

1.2.3  变形过程分析方法

为了分析孔隙结构的变化，研究变形过程，采用了变形量控制的方法，即当压缩进行到某一变形量时停止压缩变形，取出压缩后的试样，沿压缩的轴向将试样剖开，分析孔隙结构的变化情况。根据实验获得的完整应力应变曲线的特点，分别选取15%、30%、45%、60%和70%左右的变形量作为观察点。在低、中应变速率压缩时，通过GLEEBLE-1500型模拟实验机自动控制变形量；而在高应变速率压缩时，由于SHPB试验装置无法自动控制压缩变形量，实验时采用设置不同高度限位环的方法精确控制变形量，当压杆与限位环接触后受到限位环支撑而停止对试样的压缩作用，其原理如图3(b)所示。同时，在高应变速率压缩变形时，为了分析变形的动态过程，探索变形机理，采用高速摄像机记录典型应变速率下的压缩变形过程。

图4  实验采用的直接撞击式霍普金森压杆实验技术原理示意图

Fig. 4  Schematic diagram of direct-impact split Hopkinson pressure bar

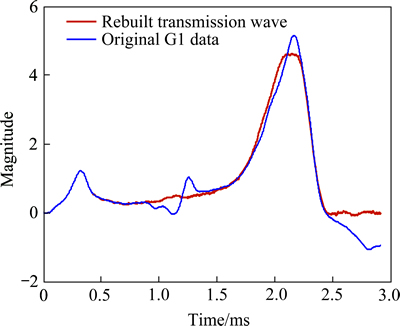
图5  利用直接撞击式霍普金森压杆实验技术获得的典型信号

Fig. 5  Typical signal obtained by direct-impact split Hopkinson pressure bar

2  结果与讨论

2.1  压缩变形过程

图6所示为实验获得的典型藕状多孔镁压缩应 力-应变曲线。由图6可以看出，尽管纯镁是典型的塑性变形能力较差的材料，但藕状多孔镁的压缩曲线并不同于致密纯镁的，致密纯镁在压缩时会在不大的压缩变形量时即会沿与压缩方向呈45°左右的滑移面发生断裂失效，所以压缩变形量一般较小；而藕状多孔镁则可以发生变形量在80%以上的连续变形，这显然与藕状多孔镁材料存在大量孔隙有关，为了进一步弄清藕状多孔镁与致密镁迥异的力学特点，需要研究其压缩过程中的变形行为。

与其他多孔材料相似，藕状多孔镁的压缩应力-应变曲线也分为3个明显的阶段：弹性阶段、应力平台阶段和密实化阶段。垂直于气孔方向压缩条件下的应力-应变曲线与平行于气孔方向压缩时的曲线明显不同，没有出现明显的应力峰值^[19]，而是表现出与藕状多孔铜类似的变化特点。这表明藕状多孔镁力学性能受压缩方向影响显著，具有明显的各向异性。

2.2  应变速率对压缩变形行为的影响

2.2.1  较低应变速率条件下的变形过程

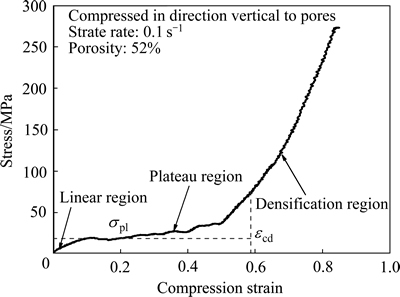
图6  典型的藕状多孔金属镁压缩应力-应变曲线

Fig. 6  Typical compressive stress-strain curve of lotus-type porous magnesium

图7所示为在应变速率为1×10^-3 s^-1条件下垂直于气孔方向压缩时藕状多孔镁经过不同变形量后的孔隙形貌。当压缩变形量较小时，气孔发生变形形成椭圆形。当变形量继续增加时，气孔发生不均匀变形，从图7(b)可以看出，当压缩变形量到15%时，已经有些气孔孔壁发生弯曲坍塌并逐步发生闭合，但有的气孔却仅发生较小的变形，即气孔并不是均匀地发生塌陷和闭合，而是在试样中形成与压缩方向垂直的先变形带，在该变形带内，气孔先发生闭合。随着变形量增大，变形带不断增加，最后达到密实化。在上述孔壁弯曲塌陷过程中，可以看到有些孔壁会发生局部断裂，但数量较少，因而垂直于气孔方向压缩时没有出现平行于气孔方向压缩时的应力峰值。当变形量到达60%时，试样整体已经闭合，只有少量气孔没有闭合。当变形量到达70%时，试样已经完全闭合。

图7  应变速率为1×10^-3 s^-1时藕状多孔镁在不同应变量下压缩试样的纵截面形貌

Fig. 7  Longitudinal-sectional morphologies of lotus-type porous magnesium compressed at strain rate of 1×10^-3 s^-1 in direction vertical to pores at nominal strain of 0(a), 0.15(b), 0.30(c), 0.45(d), 0.60(e) and 0.70(f)

图8所示为应变速率进一步增大到30 s^-1条件下垂直于气孔方向压缩时藕状多孔镁经过不同变形量后的孔隙形貌。从图8中可以明显看出，在应变速率增大到30 s^-1时，与低应变速率时相似，气孔也是先发生椭圆化变形，然后部分气孔的孔壁率先向气孔内发生弯月形塌陷并形成先变形带，随后变形带不断产生，从而逐步实现密实化。

2.2.2  高应变速率条件下的变形过程

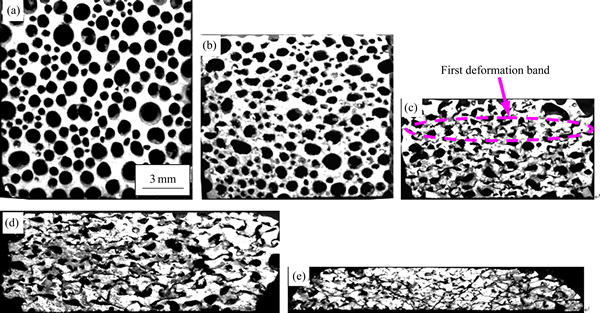
图8  应变速率为30 s^-1 时藕状多孔镁在不同应变量下压缩试样的纵截面形貌

Fig. 8  Longitudinal-sectional morphologies of lotus-type porous magnesium compressed at strain rate of 30 s^-1 in direction vertical to pores at nominal strain of 0(a), 0.15(b), 0.30(c), 0.45(d) and 0.60(e)

图9  应变速率为950 s^-1时藕状多孔镁在不同应变量下压缩试样的纵截面形貌

Fig. 9  Longitudinal-sectional morphologies of lotus-type porous magnesium compressed at strain rate of 950 s^-1 in direction vertical to pores at nominal strain of 0(a), 0.15(b), 0.30(c), 0.45(d), 0.60(e) and 0.70(f)

图9所示为在高应变速率条件下垂直于气孔方向压缩时藕状多孔镁经过不同变形量后的孔隙形貌。由图9可以发现，藕状多孔镁在高应变速率下变形后的孔隙形貌与低、中应变速率条件下有一些相似之处，即，同样是气孔先经过椭圆化变形，并且也可观察到局部变形带和孔壁的弯曲断裂。但又存在明显的不同，即在高应变速率下试样内部先变形带是沿试样对角线方向，并随着压缩进行不断向与变形带垂直的方向扩展，而在较低应变速率下，先变形带与压缩方向垂直(见图9中③虚线框所示)。

2.3  应变速率对压缩力学性能的影响

2.3.1  应变速率对压缩应力-应变曲线的影响

为了研究应变速率对藕状多孔镁沿垂直于气孔方向压缩应力-应变曲线的影响，在应变速率为1×10^-3~ 1650 s^-1范围内选取8个不同的应变速率进行了压缩实验。图10所示为垂直于气孔方向压缩时应变速率对藕状多孔镁应力-应变曲线的影响。由图10可知，压缩方向垂直于气孔方向时，不同应变速率下藕状多孔镁的应力-应变曲线变化趋势一致，都包括线弹性阶段、低应力平台阶段和密实化阶段。总体上，平台区应力值较低，基本上低于25 MPa，平台区在应变为0.05~0.6之间，且应力随应变增加在密实化之前一直缓慢增大，应力-应变曲线上均无应力峰值出现。在压缩变形量小于0.4时，随应变速率增大，应力-应变曲线总体上先有所抬升，但当应变速率增大到450 s^-1以上时，应力-应变曲线又有所降低，即垂直于气孔方向压缩时，藕状多孔镁的应力-应变曲线受应变速率的影响较明显，但在较低和高应变速率下的变化趋势相反。应变速率对应力-应变曲线影响的另一个特点是，当压缩变形量大于0.4时，随压缩变形量增加，高应变速率下的应力增加显著快于较低应变速率下的值。

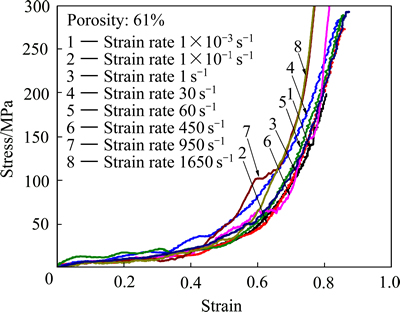
图10  垂直于气孔压缩时应变速率对藕状多孔镁压缩应 力-应变曲线的影响

Fig. 10  Effects of strain rates on stress-strain curves of lotus-type porous magnesium compressed in direction vertical to pores

2.3.2  应变速率对平台应力和密实化起始应变的影响

本实验中采用能量学方法确定密实化起始应变ε_cd，即利用材料的压缩应力、应变数据通过式(3)获得ω-ε曲线(ω为吸能效率；ε为应变)，将曲线中最大ω值所对应的应变作为密实化起始应变，如图11所示。这里ω反映的是多孔材料的能量吸收效率，当多孔材料开始密实化时，能量吸收效率开始下降，因此，最大值ω_max所对应的应变即为密实化起始应变ε_cd：

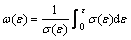                        (3)

通过对密实化起始应变的计算发现不同应变速率下藕状多孔镁的ε_cd均不大于0.5，同时，考虑到图10所示应力应变曲线的特点，即在应变小于0.1时，曲线斜度较大会影响平台应力，因此，将0.1~0.5应变范围的平均应力作为平台应力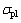，按式(4)计算：

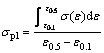                            (4)

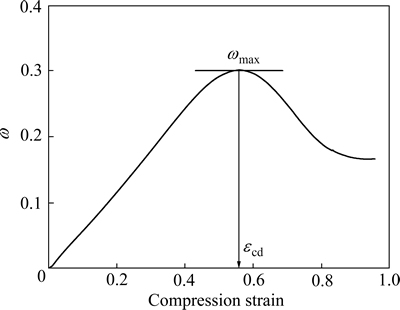
图11  能量法确定藕状多孔铜密实化起始应变示意图

Fig. 11  Schematic diagram of energetic method used to calculate densification initial strain of lotus-type porous magnesium

表1所列为垂直于气孔方向压缩时应变速率对孔隙率为61%的藕状多孔镁的平台应力的影响。参照泡沫材料平台应力研究中的处理方法，将藕状多孔镁在不同应变速率下的平台应力相对于应变速率为1×10^-3 s^-1时的数值增加20%以上作为判断其具有应变速率敏感性效应的依据。从表1中数据可以看出，压缩垂直于气孔方向的藕状多孔镁的平台应力具有一定的应变速率敏感性，孔隙率一定时，随着应变速率的变化，平台应力发生明显的改变。与应变速率为1×10^-3 s^-1时相比，当应变速率增大时，总体上平台应力增大，特别是当应变速率大于1 s^-1时，平台应力表现出比较明显的应变速率硬化效应。但当应变速率进一步增大到950 s^-1以上时，平台应力又开始随应变速率增加而下降，与较低应变速率时相比表现出相反的趋势。

表1  应变速率对垂直于气孔方向压缩时藕状多孔镁的平台应力的影响(孔隙率为61%)

Table 1  Effect of strain rate on platform stress of lotus-type magnesium with porosity of 61% compressed vertical to pores

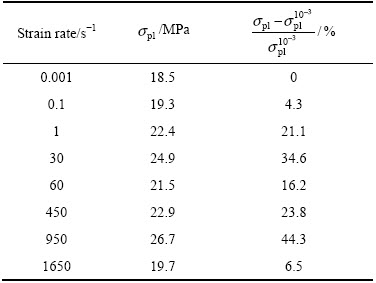
图12所示为垂直于气孔方向压缩时应变速率对藕状多孔镁的密实化起始应变的影响。由图12可以看出，在垂直于气孔方向压缩时，密实化起始应变值明显小于平行于气孔方向压缩时的值，在较低应变速率时，略小于试样的孔隙率(61%)。从上述变形行为的研究结果可知，垂直于气孔方向压缩时藕状多孔镁的变形方式主要是气孔压扁和孔壁向气孔内部弯曲、塌陷， 逐步填充孔隙部位达到密实化，这种方式比较容易实现密实化，所以密实化起始应变没有超过试样的孔隙率。在较低应变速率时，藕状多孔镁的密实化起始应变数据相差不大，但在高应变速率时，藕状多孔镁的密实化起始应变比较低应变速率时较明显增大。这是由于高应变速率时主要是气孔直接压扁、闭合的方式实现密实化，在压扁变形的最后阶段进一步压实的难度较大。

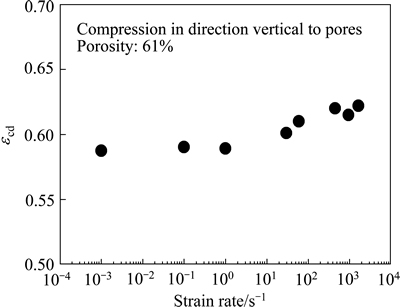
图12  应变速率对起始密实化应变的影响

Fig. 12  Effects of strain rates on densification initial strains of lotus-type porous magnesium

综上所述，应变速率对藕状多孔镁的平台应力的影响比较明显，但对密实化起始应变的影响较小。

2.4  分析与讨论

如前所述，藕状多孔金属的特点之一是其孔隙结构取向分布，具有明显的各向异性，这种结构特点可能会对其不同方向的变形行为和力学性能产生影响。从前期研究可知^[19]，在沿平行于气孔方向压缩变形时，其变形方式主要是通过孔壁局部坍塌，进而向气孔中坍塌，并逐步实现密实化。而从本研究结果可知，垂直于气孔方向压缩时，其主要变形过程是气孔以不同的方式被压扁、坍塌、密实化，具体的变形方式受变形条件影响而有所不同，具体分析如下。

以单个气孔单元作为研究对象，分析在垂直于气孔方向压缩时的变形情况。图13所示为垂直于气孔压缩时气孔单元在不同应力状态下的变形方式。多孔压缩试样在垂直于气孔轴向的单向压应力作用下，除了试样边部较小的自由变形区内的气孔主要受到沿压缩方向的压应力以外，压缩试样内部的气孔不仅要受到沿压缩方向的应力，由于相邻气孔单元的相互作用，还受到与压缩方向垂直的压缩应力的作用。当试样经受较小压缩变形时，由于变形初始阶段沿压缩方向的应力是主应力，在此应力的作用下，气孔孔壁发生弯曲，气孔变为椭圆形。随着压缩变形量的增大，与压缩方向垂直方向上的应力不断增大。在沿垂直方向上应力明显较大的条件下，形成长轴沿水平方向的椭圆气孔；在水平方向的应力明显较大的局部区域形成长轴沿垂直方向的椭圆形气孔；在两个方向上的应力稍有差别的条件下，椭圆气孔长轴则与水平方向成一定的夹角。随着变形量继续增大，由于孔壁的不均匀性和镁的塑性变形能力较差，在孔壁较薄弱的地方容易发生孔壁的剪切断裂，气孔长轴也会发生一定的转向。当压缩变形量超过一定数值后，藕状多孔镁变形进入密实化阶段。断裂孔壁填充气孔，气孔孔隙被压缩到很小，从压缩变形之后试样的纵截面照片可以看出，最终的气孔长轴方向朝向有水平方式、垂直方式和斜排方式。

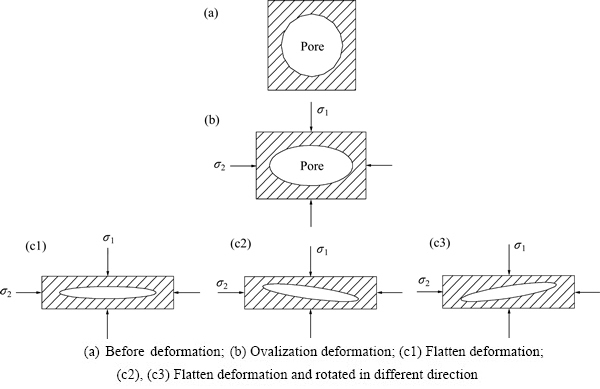
图13  垂直于气孔压缩时气孔单元在不同应力状态下的变形方式

Fig. 13  Deformation mode of single pore under different stress condition compressed vertical to pore

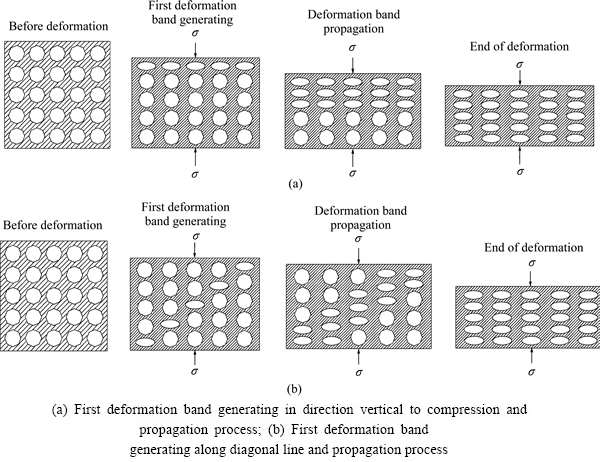
图14  垂直于气孔方向压缩时藕状多孔镁的变形方式

Fig. 14  Schematic diagrams of two deformation modes of lotus-type porous magnesium compressed in direction vertical to pores

当压缩时的应变速率变化时，综上所述可知，在应变速率较低时(≤30 s^-1)，压缩变形过程中气孔的变形方式没有观察到明显的变化，主要是试样内部部分气孔先产生压扁、塌陷等变形，形成沿与压缩方向垂直的方向先变形带，之后变形带不断产生，直至密实化(见图14(a))。当应变速率达到950 s^-1以上时，可以观察到在压缩变形过程中试样内部气孔的变形方式发生了较明显的变化，即气孔首先沿着与压缩方向呈约45°的对角线方向发生压扁和塌陷变形，形成先变形带，然后沿与变形带垂直的方向扩展(见图14(b))。相关研究表明，在高速应变速率下压缩时，高速压头作用到压缩试样时，往往会产生明显的冲击波效应，冲击波从压头与试样接触的一端向另一端传播，引起压缩试样在与高速压头接触部位率先发生局部变形，且局部变形随着冲击波从一端向另一端的传播而不断向前推进，引起试样发生不均匀变形。为了分析藕状多孔镁试样在高速压缩过程中是否受到冲击波的显著影响，采用高速摄像机对藕状多孔镁高应变速率压缩变形过程进行了高速摄像。图15所示为高速摄像机记录的藕状多孔镁垂直于气孔方向压缩时不同压缩变形量时的图像。从图15可以看出，压缩试样并没有发生从一端向另一端的局部变形，而是总体上仍然发生较为均匀的压缩变形，这表明在应变速率达到950 s^-1时，藕状多孔镁在垂直于气孔方向压缩时并没有受到冲击波效应的明显影响。因此，在垂直于气孔方向压缩时，藕状多孔镁在较低应变速率下和高应变速率下表现出不同的变形行为，这可能主要与不同应变速率下试样内部的应力分布状态和压缩变形过程中变形协调的难易程度有关。

图15  高速摄像机记录的藕状多孔镁垂直于气孔方向压缩时的变形过程

Fig. 15  Compressive deformation process of lotus-type porous magnesium at strain rate of 950 s^–1 recorded by high-speed camera with shooting speed of 50000 frames/s and different compressive deformation degrees (Arrows mark samples)

3  结论

1) 垂直于气孔方向压缩时，藕状多孔镁的应力-应变曲线分为应力线性增加的弹性阶段、应力缓慢增加的平台阶段和应力急剧增加的密实化阶段，应力随应变增加持续增大，无应力峰值或下降。

2) 垂直于气孔方向压缩时应变速率对藕状多孔镁的变形行为影响显著，在应变速率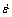＜60 s^-1条件下的主要变形方式为气孔先发生椭圆化变形，然后部分气孔的孔壁率先向气孔内发生弯月形塌陷并形成垂直于压缩方向的先变形带，随后变形带不断产生，从而逐步实现密实化；而在较高应变速率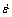为450~1650 s^-1条件下，变形方式虽然气孔也是先后发生椭圆化、孔壁向气孔内的弯曲塌陷等变形并形成先变形带，但先变形带沿试样对角线方向形成率先形成，并随压缩进行不断向与对角线垂直的方向扩展。

3) 应变速率对藕状多孔镁的力学性能有较明显的影响，其影响机制主要是由于不同应变速率时气孔的变形方式发生了变化，高应变速率时受冲击波效应的影响不明显。

REFERENCES

[1] DEGISCHER H P, KRISZT B. 多孔泡沫金属[M]. 左孝青, 周 芸, 译. 北京: 化学工业出版社, 2005: 1-4.

DEGISCHER H P, KRISZT B. Handbook of cellular metals[M]. ZUO Xiao-qing, ZHOU Yun, transl. Beijing: Chemical Industry Press, 2005: 1-4.

[2] BANHART J. Manufacture, characterisation and application of cellular metals and metal foams[J]. Progress in Materials Science, 2001, 46(6): 559-632.

[3] GIBSON L J, ASHBY M F. Cellular Solids: Structure and Properties[M]. 2 nd ed. Cambridge UK: Cambridge University Press, 1999: 1-10.

[4] SHAPOVALOV V. Method of manufacturing porous articles: United States, 5181549[P]. 1993-06-26.

[5] NAKAJIMA H, IDE T. Fabrication of porous copper with directional pores through thermal decomposition of compounds[J]. Metallurgical and Materials Transactions A, 2008, 39(2): 390-394.

[6] NAKAJIMA H. Fabrication, properties and application of porous metals with directional pores[J]. Progress in Materials Science, 2007, 52(7):1091-1173.

[7] NAKAJIMA H, IKEDA T, HYUN S K. Fabrication of lotus-type porous metals and their physical properties[J]. Advanced Engineering Material, 2006, 6(6): 377-384.

[8] HYUN S K, NAKAJIMA H. Anisotropic compressive properties of porous copper produced by unidirectional solidification[J]. Materials Science and Engineering A, 2003, 340(12): 258-264.

[9] ICHITSUBO T, TANE M. Anisotropic elastic constants of lotus-type porous copper: Measurements and micromechanics modeling[J]. Acta Materialia, 2002, 50(16): 4105-4115.

[10] V, SINGER R F. Endogenous particles stabilization during magnesium integral foam production[J]. Advanced Engineering Materials, 2004, 6(6): 385-390.

[11] RENGER K, KAUFMANN H. Vacuum foaming of magnesium slurries[J]. Advanced Engineering Materials, 2005, 7(3): 117-123.

[12] WEN C E, YAMADA Y, SHIMOJIMA K, CHINO Y, HOSOKAWA H, MABUCHI M. Compressibility of porous magnesium foam: Dependency on porosity and pore size[J]. Materials Letter, 2004, 58(3/4): 357-360.

[13] J O, SUAREZ M A, GOODALL R, LARA-RODRIGUEZ G A, ALFONSO I, FIGUEROA I A. Manufacturing of open-cell Mg foams by replication process and mechanical properties[J]. Materials and Design, 2014, (64): 136-141.

[14] MUKAI T, KANAHASHI H, MIYOSHI T, MABUCHI M, NIEH T G, HIGASHI K. Experimental study of energy absorption in a close-celled aluminum foam under dynamic loading[J]. Scripta Materialia, 1999, 40(8): 921-927.

[15] DESHPANDE V S, FLECK N A. High strain rate compressive behaviour of aluminium alloy foams[J]. International Journal of Impact Engineering, 2000, 24(3): 277-298.

[16] DANNEMANN K A, LANKFORD J J. High strain rate compression of closed-cell aluminium foams [J]. Materials Science and Engineering A, 2000, 293(1/2): 157-164.

[17] DHARARN C K H, HAUSER F E. Determination of stress-strain characteristics at very high strain rates[J]. Experimental Mechanics, 1970, 10(6): 370-376.

[18] MONDAL D P, GOEL M D, DAS S. Compressive deformation and energy absorption characteristics of closed cell aluminum-fly ash particle composite foam[J]. Materials Science and Engineering A, 2009, 507(1/2): 102-109.

[19] 刘新华, 晏玉平, 谢建新. 应变速率对藕状多孔镁平行于气孔方向压缩变形行为与力学性能的影响[J]. 中国有色金属学报, 2016, 26(4): 747-757.

LIU Xin-hua, YAN Yu-ping, XIE Jian-xin. Effect of strain rate on the compressive deformation behaviors and mechanical properties of lotus-type porous magnesium in the direction parallel to pores[J]. The Chinese Journal of Nonferrous Metals, 2016, 26(4): 747-757.

Effect of strain rate on compressive deformation behaviors and mechanical properties of lotus-type porous magnesium in direction vertical to pores

LIU Xin-hua, YAN Yu-ping, XIE Jian-xin

(Institute for advanced Materials and Technology, University of Science and Technology Beijing, Beijing 100083, China)

Abstract: Lotus-type porous magnesium was fabricated by unidirectional solidification, and the compressive experiments were subsequently conducted in the compressive direction vertical to the pores at strain rate in range of 1×10^-3-1650 s^-1 using GLEEBLE-1500 materials simulation system and split Hopkinson pressure bar (SHPB). The effects of strain rate on the compressive deformation behaviors and mechanical properties of lotus-type porous magnesium were investigated. The results indicate that the compressive deformation process of lotus-type porous magnesium consists of a linear elastic stage, a plateau stage and a densification stage at various strain rates, and the stress increases with the increase of strain without the stress peak. The strain rates have significant effects on the compressive deformation behaviors of lotus-type magnesium in the compressive direction vertical to the pores. When compressed at a lower strain rate less than 60 s^-1, lotus-type magnesium deforms mainly in the way, the round pore was firstly flatten to ellipse, then the wall of some pores earlier starts to collapse into the hole by a crescent-shaped bending and forms a first deformation band which is vertical to compressed direction. When compression continues, the deformation band forms continually. However, when compressed at high strain rates between 450 s^-1 and 1650 s^-1, the deformation band first forms along the diagonal direction and expands along the direction vertical to the diagonal. The strain rates have obvious influence on the mechanical property, and the main mechanism is that the deformation way of pore at lower strain rate is different from that at high strain rate.

Key words: lotus-type porous magnesium; strain rate; deformation behaviors; mechanical property; deformation mechanism

Foundation item: Project(50904004) supported by the National Natural Science Foundation of China

Received date: 2015-11-10; Accepted date: 2016-07-19

Corresponding author: XIE Jian-xin; Tel: +86-10-62332254; E-mail: jxxie@mater.ustb.edu.cn

(编辑  龙怀中)

基金项目：国家自然科学基金资助项目(50904004)

收稿日期：2015-11-10；修订日期：2016-07-19

通信作者：谢建新，教授，博士；电话：010-62332254；E-mail: jxxie@mater.ustb.edu.cn