基于蚁群算法梯式轨枕轨道减振优化研究

金浩，刘维宁

(北京交通大学 土木建筑工程学院，北京，100044)

摘要：为提高梯式轨枕轨道综合减振效果，分别将钢轨振动位移和传递到基础的总功率流作为目标函数，枕下弹性垫板动刚度、材料损耗因子、块数以及纵向轨枕横截面面积作为优化变量，使用多元连续函数蚁群算法进行优化研究。结果表明：要减少钢轨的振动位移，需要增大枕下弹性垫板动刚度、纵向轨枕的横截面面积以及枕下弹性垫板的块数，同时减小枕下弹性垫板的材料损耗因子；要减小传递到基础的总功率流，则需要减小枕下弹性垫板的动刚度和枕下弹性垫板的块数，同时增大枕下弹性垫板的材料损耗因子以及纵向轨枕的横截面面积。使用统一目标函数法将多目标函数简化为单目标函数，得到最优化结果，和目前梯式轨枕轨道使用的参数相比，钢轨振动位移优化率达50.9%，传递到基础的总功率流优化率达47.6%。

关键词：蚁群算法；梯式轨枕轨道；减振；优化；功率流

中图分类号：U213.2；TB535        文献标志码：A         文章编号：1672-7207(2012)07-2751-06

Vibration reduction optimization of ladder track based on an ant colony algorithm

JIN Hao, LIU Wei-ning

 (School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China)

Abstract: For improving the vibration reduction effect of the ladder track, research was conducted with ant colony algorithm of multivariate continuous function. Vibration displacement of rail and the total power flow of foundation were made as objective functions. Dynamic stiffness, material loss factor, the number of elastic pads under sleeper and area of longitudinal sleeper were made as design variables. The result shows that: to decrease vibration displacement of rail, dynamic stiffness, the number of elastic pads under sleeper and area of longitudinal sleeper should be increased and material loss factor of elastic pads under sleeper be decreased; to decrease total power flow of foundation, dynamic stiffness, the number of elastic pads under sleeper decreases and material loss factor of elastic pads under sleeper and area of longitudinal sleeper increases. Making multi-object to a single object with a constructor, optimization results are as follows: optimization rate of vibration displacement of rail is 50.9% and optimization rate of total power flow of foundation is 47.6% comparing with former parameters.

Key words: ant colony algorithm; ladder track; vibration reduction; optimization; power flow

随着城市轨道交通建设的蓬勃发展，由此引发的振动问题也日益突出。从大量的测试来看，作为中等减振措施的梯式轨枕轨道，能较好地降低传递到基础的振动，有效控制环境振动问题^[1]。但是，如果减振垫刚度过小，将导致钢轨的振动位移增大，产生钢轨波形磨耗问题。因此，有必要对梯式轨枕轨道减振性能进行综合优化研究。根据蚂蚁“寻找食物”的群体行为，Dorigo等^[2]于1991年最早提出了蚁群算法(Ant Colony Algorithm)的基本模型。由于蚁群算法能够快速、有效地搜寻到全域最优解，隧道施工^[3-4]、边坡稳定^[5-6]等都开展了利用蚁群算法进行优化设计的研究。但是利用蚁群算法优化轨道减振性能尚无人研究。本文作者将钢轨振动位移和传递到基础的总功率流作为目标函数，枕下弹性垫板动刚度、材料损耗因子、块数以及纵向轨枕横截面面积作为设计变量。利用多元连续函数蚁群算法，进行单目标和多目标耦合分析，综合优化梯式轨枕轨道的减振效果。

1  多元连续函数蚁群算法

蚁群算法已被许多研究证实是一种有效的离散优化算法，目前已用于求解TSP(Traveling salesman problem)^[7-8]、QAP(Quadratic assignment problem)^[9-10]等离散优化问题，得到了很好的结果。为了将蚁群算法应用于连续函数，各国学者都进行了这方面的研究，譬如基于图的蚁群算法^[11]、网格优化算法^[12]、基于密集非递阶的连续交互式蚁群算法(Continuous interacting ant colony algorithm, CIAC)^[13]和基于“觅食-返巢”机制的连续域蚁群算法^[14]等。参考陈烨^[15]的部分思想并进行修改，得到多元连续函数的蚁群算法。

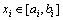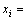
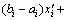
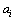设计变量， 通过简单的数学变化转化为。i为设计变量的个数， ，a_i，b_i为设计变量x_i最小值和最大值。在得到最优解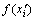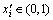，后，与目标函数边值进行比较，最终得到全域最优解。

根据不同的问题，设计变量可以取小数点后d位。对于十进制数，每一位可以取10个数(0, 1, …, 9)。对于多元函数问题，假设每个设计变量使用n_i只蚂蚁，不同设计变量之间的蚂蚁互不干扰，并行前进。假设第j只蚂蚁在第k位所取的数为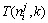。其中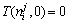表示第一步都是从0出发。如果蚂蚁j当前所在的位数为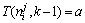，根据以下公式选择下一位数：

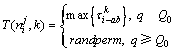
其中：q为(0, 1)的随机数，常数Q₀=0.8，randerm表示随机取(0, 1, …, 9)中的一个数，信息素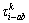表示变量x_i在k位上取b的信息数含量，初始。

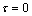每只蚂蚁走完一步后，信息素就需要局部更新：

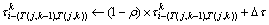
其中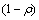：为信息素残留因子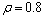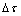，，为信息素增加量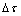，=0.8。

当所有蚂蚁根据小数点位数走完一个循环，则信息素进行全局更新：

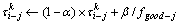
其中：常数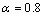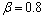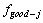，，为一次循环的最优解。

经过n次循环迭代，即可求得全域最优解。基于以上原理，利用Matlab编制得到多元连续函数蚁群算法优化程序。

2  梯式轨枕轨道参数研究

2.1  梯式轨枕轨道模型

梯式轨枕轨道模型选用60 kg/m钢轨，长l_rail=6.15 m，单根钢轨质量m_rail=369 kg；轨下弹性垫板间距0.625 m，端部弹性垫板距离相应轨枕端面0.262 5 m (共2×10块)，动刚度k_ur=60 MN/m，材料损耗因子η_ur=0.2；纵向轨枕密度ρ_ls=2 680 kg/m³，截面面积S_ls，长l_ls=6.15 m；枕下弹性垫板动刚度k_us，材料损耗因子η_us，块数n_um。梯式轨枕轨道模型如图1所示。

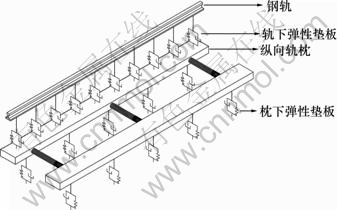
图1  梯式轨枕轨道模型

Fig.1  Model of ladder track

将梯式轨枕轨道系统划分为钢轨子系统、轨下弹性垫板子系统、纵向轨枕子系统、枕下弹性垫板子系统以及基础子系统，四端参数如表1所示。其中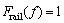和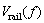为钢轨子系统输入力和速度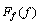，和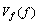为通过枕下弹性垫板传递到基础子系统的力和速度，如图2所示。

将基础简化成无限大板，基础子系统阻抗为：

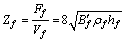。其中：基础密度ρ_f=2 680

kg/m³，基础厚度h_f=0.3 m，弯曲刚度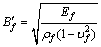，基础弹性模量E_f=40 GPa，泊松比

。

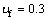表1  梯式轨枕轨道子系统四端参数

Table 1  Four-terminal parameters of ladder track subsystems

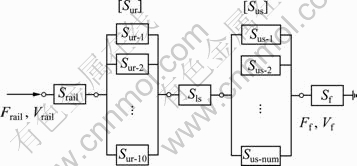
图2  梯式轨枕轨道四端网络

Fig.2  Four-terminal network of ladder track

,

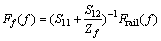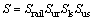
根据标准^[16-17]，分析频段取1~200 Hz，得到钢轨的位移：

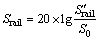
传递到基础的总功率流：

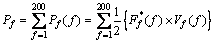
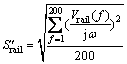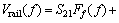
其中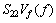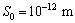：， ，，*为取共轭。

2.2  梯式轨枕轨道参数研究

将枕下弹性垫板动刚度k_us、材料损耗因子η_us、块数n_um以及纵向轨枕横截面面积S_1s作为设计变量。枕下弹性垫板动刚度10 MN/m≤k_us≤100 MN/m，?k_us=10 MN/m；枕下弹性垫板材料损耗因子0.025≤η_us≤0.25，?η_us=0.025；枕下弹性垫板块数10≤n_um≤20，?n_um=2；纵向轨枕横截面面积0.08 m²≤S_1s≤0.098 m²，?S_1s=0.002 m²。将钢轨振动位移S_rail和传递到基础的总功率流P_f作为控制目标，S_rail和P_f随梯式轨枕轨道参数变化规律如图3~10所示。可见：对于设计变量k_us，η_us和n_um，钢轨振动位移和传递到基础的总功率流是相互矛盾的。在优化其中一个控制目标时，势必导致另一个控制目标劣化。纵向轨枕横截面面积S_ls的增大，可以同时降低钢轨振动位移和传递到基础的总功率流。

3  蚁群算法验证与优化

3.1  单目标蚁群算法验证

利用自编程序(多元连续函数蚁群算法优化程序)，对控制目标钢轨振动位移和传递到基础的总功率流，分别进行优化设计，目标函数达到最小值时，设计变量取值如表2所示。可以看出，优化得到的结果和参数分析所得出的结果是一致的。本程序只使用了较小的设计位数、少量的蚂蚁数和迭代次数，就得到了全域最优解，计算时间和收敛性都较好。

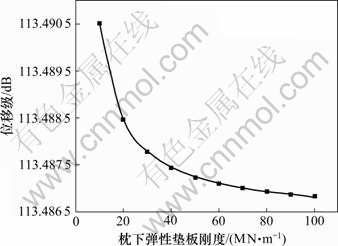
图3  S_rail随着k_us的变化

Fig.3  Variation of S_rail with k_us

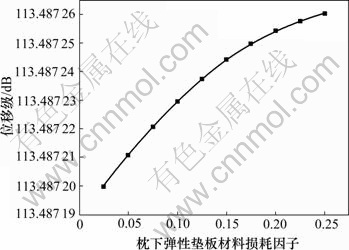
图4  S_rail随着η_us的变化

Fig.4  Variation of S_rail with η_us

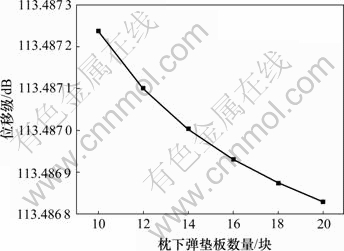
图5  S_rail随着n_um的变化

Fig.5  Variation of S_rail with n_um

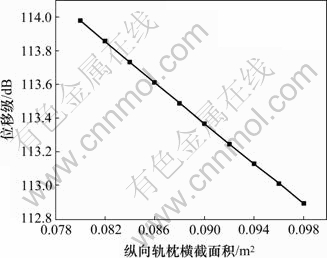
图6  S_rail随着S_ls的变化

Fig.6  Variation of S_rail with S_ls

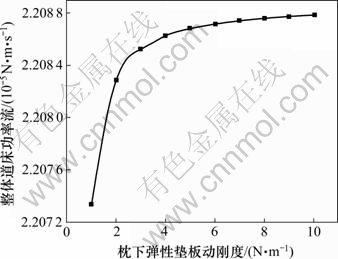
图7  P_f随着k_us的变化

Fig.7  Variation of P_f with k_us

图8  P_f随着η_us的变化

Fig.8  Variation of P_f with η_us

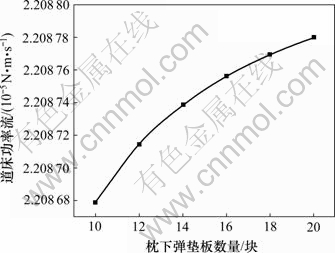
图9  P_f随着n_um的变化

Fig.9  Variation of P_f with n_um

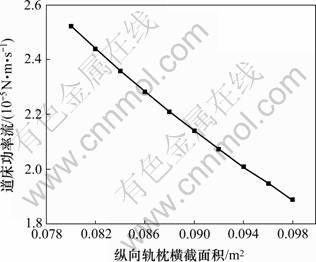
图10  P_f随着S_ls的变化

Fig.10  Variation of P_f with S_ls 

表2  单目标优化结果

Table 2  Optimization results of single object

3.2  多目标蚁群算法优化

采用统一目标函数法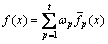，，式中：

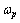为各分目标权重系数，此处取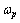(p=1, 2, …, t)=1。构造函数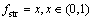，则单目标函数可以转化为

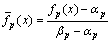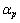， 式中：和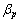为对应目标函

数的最小值和最大值。

传递到基础的总功率流：最大值为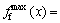 2.52×10^-5 N·m/s，最小值为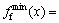1.89×10^-5 N·m/s，相差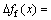6.3×10^-6 N·m/s；钢轨振动位移：最大值为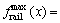113.98 dB，最小值为 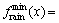12.88 dB，相差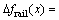1.1 dB。梯式轨枕轨道目前使用参数为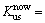5×10⁷ N/m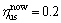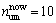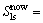，，，0.088 m²，则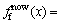2.21×10^-5 N·m/s和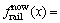113.49 dB。

使用多目标蚁群算法优化，得到统一目标函数的最优解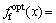：1.91×10^-5 N·m/s和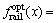112.93 dB，变量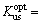3.8×10⁷ N/m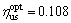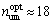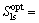，，，0.097 m²。

钢轨振动位移优化率为：

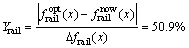
传递到基础的总功率流优化率为：

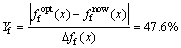
4  结论

(1) 要减少钢轨的振动位移，需要增大枕下弹性垫板动刚度、纵向轨枕的横截面面积以及枕下弹性垫板的数量，同时减小枕下弹性垫板的材料损耗因子；要减小传递到基础的总功率流，则需要减小枕下弹性垫板的动刚度和枕下弹性垫板的数量，同时增大枕下弹性垫板的材料损耗因子以及纵向轨枕的横截面面积。

(2) 使用统一目标函数法将多目标函数简化为单目标函数，得到最优化结果：和目前梯式轨枕轨道使用的参数相比，钢轨振动位移优化率达50.9%，传递到基础的总功率流优化率达47.6%。

参考文献：

[1] 王文斌, 刘维宁, 贾颖绚, 等. 更换减振扣件前后地铁运营引起地面振动的研究[J]. 中国铁道科学, 2010, 31(4): 87-92.

WANG Wen-bin, LIU Wei-ning, JIA Ying-xuan, et al. Research on the vibration of the ground caused by metro train operation before and after changing the damping fasteners[J]. Chian Railway Science, 2010, 31(1): 87-92.

[2] 段海滨. 蚁群算法原理及其应用[M]. 北京: 科学出版社, 2005: 8.

DUAN Hai-bin. Ant colony algorithms: theory and applications[M]. Beijing: Science Press, 2005:8.

[3] 韦凯, 宫全美, 周顺华. 隧道长期不均匀沉降预测的蚁群算法[J]. 同济大学学报: 自然科学版, 2009, 37(8): 993-998.

WEI Kai, GONG Quan-mei, ZHOU Shun-hua. Ant colony algorithms of long-term uneven settlement prediction in tunnel[J]. Journal of Tongji University: Natural Science, 2009, 37(8): 993-998.

[4] 高玮, 郑颖人. 蚁群算法及其在硐群施工优化中的应用[J]. 岩石力学与工程学报, 2002, 21(4): 471-474.

GAO Wei, ZHEN Ying-ren. Ant colony algorithm and its application into optimization of construction order for underground house groups[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(4): 471-474.

[5] 李亮, 迟世春, 林皋. 基于蚁群算法的复合形法及其在边坡稳定分析中的应用[J]. 岩土工程学报, 2004, 26(5): 691-696.

LI Liang, CHI Shi-chun, LIN Gao. The complex method based on ant colony algorithm and its application to the slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(5): 691-696.

[6] 陈昌富, 龚晓南, 王贻荪. 自适应蚁群算法及其在边坡工程中的应用[J]. 浙江大学学报: 工学版, 2003, 37(5): 566-569.

CHEN Chang-fu, GONG Xiao-nan, WANG Yi-sun. Adaptive colony algorithm and its application to the slope engineering[J]. Journal of Zhejiang University: Engineering Science, 2003, 37(5): 566-569.

[7] Dorigo M, Gambardella M L. Ant colony system: a cooperative learning approach to the traveling salesman problem[J]. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 53-66.

[8] Dorigo M, Maniezzo V, Colorni A. Ant system: Optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part: B, 1996, 26(1): 29-41.

[9] Maniezzo V, Colorni A. The ant system applied to the quadratic assignment problem[J]. IEEE Transactions on Knowledge and Data Engineering, 1999, 11(5): 769-778.

[10] Gambardella M L, Taillard D E, Dorigo M. Ant colonies for the quadratic assignment problem[J]. Journal of the Operational Research Society, 1999, 50(2): 167-176.

[11] Walter Gutjahr J. A graph-based ant system and its convergence[J]. Future Generation Computer Systems, 2000, 16(9): 873-888.

[12] 高尚, 钟娟, 莫述军. 连续优化问题的蚁群算法研究[J]. 微机发展, 2003, 13(1): 21-22, 69.
GAO Shang, ZHONG Juan, MO Shu-jun. Research on ant colony algorithm for continuous optimization problem[J]. Microcomputer Development, 2003, 13(1): 21-22, 69.

[13] Dero J, Siarry P. Continuous interacting ant colony algorithm based on dense heterarchy[J]. Future Generation Computer Systems, 2004, 5(20): 841-856.

[14] 金浩, 刘维宁. 基于觅食-返巢机制连续域蚁群算法[J]. 计算机工程与应用, 2012, 48(1): 24-26.

JIN Hao, LIU Wei-ning. Ant Colony Algorithm for continuous function based on foraging-homing mechanism[J]. Computer Engineering and Application, 2012, 48(1): 24-26.

[15] 陈烨. 用于连续函数优化的蚁群算法[J]. 四川大学学报: 工程科学版, 2004, 36(6): 117-120.

CHEN Ye. Ant colony system for continuous function optimization[J]. Journal of Sichuan University: Engineering Science Edition, 2004, 36(6): 117-120.

[16] JGJ/T 170—2009, 城市轨道交通引起建筑物振动与二次噪声限值及其测量方法标准[S].

JGJ/T 170—2009, Standard for limit and measuring method of building vibration and secondary noise caused by urban rail transit[S].

[17] GB/T 13441.2—2008/ISO 2631-2: 2003, 机械振动与冲击人体暴露于全身振动的标准(第二部分): 建筑物内的振动 (1 Hz~80 Hz)[S].

GB/T 13441.2—2008/ISO 2631-2: 2003, Mechanical vibration and shock-evaluation of human exposure to whole-body vibration (Part 2): Vibration in building (1 Hz to 80 Hz)[S].

(编辑 陈爱华)

收稿日期：2011-08-09；修回日期：2011-10-27

基金项目：国家自然科学基金资助项目(51008017)；中央高校基本科研业务费专项资金资助项目(2012YJS072)

通信作者：金浩(1986-), 男，浙江诸暨人，博士研究生，从事新型轨道减振措施智能优化研究；电话：13811864769；E-mail：jiaodajinhao@gmail.com