节理面JRC-JCS非线性准则的数值计算方法
吴启红,徐青,雍军,廖贤
(成都大学 城乡建设学院,四川 成都,610106)
摘要:为了采用JRC-JCS模型描述岩体节理非线性强度特征,首先,研究JRC-JCS强度非线性模型参数和Mohr-Coulomb强度线性模型参数之间的关系;然后,探讨JRC-JCS模型的数值实现方法,并通过节理室内剪切试验结果对数值模拟结果进行验证;最后,分析非线性模型参数对节理剪切强度的影响。研究结果表明:黏结力c和内摩擦角 随节理粗糙系数JRC的增大而呈非线性增大;黏结力c随岩体压缩强度JCS的增大呈线性增大,而内摩擦角
随节理粗糙系数JRC的增大而呈非线性增大;黏结力c随岩体压缩强度JCS的增大呈线性增大,而内摩擦角 随JCS的增大而呈非线性增大。JRC的变化对于剪切强度的影响要比JCS的影响突出;验证了JRC-JCS模型数值计算方法的正确性。
随JCS的增大而呈非线性增大。JRC的变化对于剪切强度的影响要比JCS的影响突出;验证了JRC-JCS模型数值计算方法的正确性。
关键词:节理面;JRC-JCS模型;数值计算;非线性
中图分类号:TU821 文献标志码:A 文章编号:1672-7207(2013)09-3829-05
Numerical embedding in FLAC3D of JRC-JCS model of joint plane
WU Qihong, XU Qing, YONG Jun, LIAO Xian
(School of Urban and Rural Construction, Chengdu University, Chengdu 610106, China)
Abstract: In order to describe the nonlinear strength characteristic of rock mass joint plane by JRC-JCS model, firstly, the relations among the parameters of JRC-JCS model and Mohr-Coulomb model were studied, then the numerical realization method of JRC-JCS model was analyzed. And the results from the numerical simulation were verified by the results from the lab shear tests of joint plane. Finally, the effect of the parameters of the nonlinear model to the shear strength of joint plane was analyzed. The results show that cohesion c and friction angle  increase in the nonlinear form with the increase of joint rough coefficient JRC; with the increase of rock compression strength JCS, the cohesion increases in the linear form, but
increase in the nonlinear form with the increase of joint rough coefficient JRC; with the increase of rock compression strength JCS, the cohesion increases in the linear form, but  increases in the nonlinear form. JRC has larger impact on the shear strength of joint plane than JCS. Validation of numerical calculation method for JRC-JCS model is correct.
increases in the nonlinear form. JRC has larger impact on the shear strength of joint plane than JCS. Validation of numerical calculation method for JRC-JCS model is correct.
Key words: joint plane; JRC-JCS model; numerical calculation method; nonlinear
目前,对于岩体强度特征描述的研究大部分采用Mohr-Coulomb线性模型[1-3],大部分计算软件也都基于Mohr-Coulomb模型,该模型用黏结力c和内摩擦角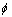 表征岩体的强度。但岩体中广泛分布着节理面,导致岩体强度呈现非线性特征[4-5],而线性模型无法反映该特征,存在一定局限性,因此,一些学者引入非线性模型如Hoek-Brown[6-8]对岩体强度进行描述,如:林杭等[6-7]拓展了强度折减法在Hoek-Brown模型中的应用;蒋青青[8]建立了Hoek-Brown非线性模型下的边坡稳定性点安全系数;朱自强等[9]研究了层状岩体的压缩破坏特征,并建立了相应的非线性理论描述模型。这些研究对岩体强度非线性进行了描述,而对于岩体节理面,普遍认为JRC-JCS模型能够较好地描述节理特征[10-12],它是Barton等[11]通过大量节理岩体的剪切试验提出的,但目前主要采用理论和试验的方法对该模型进行研究,而较少研究其数值计算方法。为此,本文作者首先通过理论推导建立JRC-JCS模型和Mohr-Coulomb模型参数之间的关系,然后,探讨JRC-JCS模型的数值实现方法以及实施过程,并通过岩体节理剪切试验验证数值方法的可靠性;最后,分析JRC-JCS模型参数对于节理剪切强度的影响。
表征岩体的强度。但岩体中广泛分布着节理面,导致岩体强度呈现非线性特征[4-5],而线性模型无法反映该特征,存在一定局限性,因此,一些学者引入非线性模型如Hoek-Brown[6-8]对岩体强度进行描述,如:林杭等[6-7]拓展了强度折减法在Hoek-Brown模型中的应用;蒋青青[8]建立了Hoek-Brown非线性模型下的边坡稳定性点安全系数;朱自强等[9]研究了层状岩体的压缩破坏特征,并建立了相应的非线性理论描述模型。这些研究对岩体强度非线性进行了描述,而对于岩体节理面,普遍认为JRC-JCS模型能够较好地描述节理特征[10-12],它是Barton等[11]通过大量节理岩体的剪切试验提出的,但目前主要采用理论和试验的方法对该模型进行研究,而较少研究其数值计算方法。为此,本文作者首先通过理论推导建立JRC-JCS模型和Mohr-Coulomb模型参数之间的关系,然后,探讨JRC-JCS模型的数值实现方法以及实施过程,并通过岩体节理剪切试验验证数值方法的可靠性;最后,分析JRC-JCS模型参数对于节理剪切强度的影响。
1 理论推导
1.1 JRC-JCS模型与Mohr-Coulomb模型参数之间的关系
JRC-JCS模型是Barton等[11]通过大量节理岩体的剪切试验提出的,其形式为
 (1)
(1)
式中: 为岩体的剪切强度;
为岩体的剪切强度; 为节理的正应力;
为节理的正应力; 为岩体基本摩擦角,可取为30°[11];JRC为节理粗糙系数,其取值与节理粗糙形态有关;JCS为岩体压缩强度,在低应力条件下,JCS对抗剪强度影响较小;随着法向应力增大,JCS的影响亦增大。
为岩体基本摩擦角,可取为30°[11];JRC为节理粗糙系数,其取值与节理粗糙形态有关;JCS为岩体压缩强度,在低应力条件下,JCS对抗剪强度影响较小;随着法向应力增大,JCS的影响亦增大。
Mohr-Coulomb模型的形式为
 (2)
(2)
从式(2)可以看出:Mohr-Coulomb模型中,节理面的强度主要取决于强度参数黏结力c和内摩擦角 。对式(2)进行求导,可得
。对式(2)进行求导,可得
 (3)
(3)
联立式(1)和式(3),可得[8]
 (4)
(4)
式中: ;
;
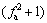 。
。
对式(4)进行三角关系变换得:
 (5)
(5)
 (6)
(6)
 (7)
(7)
 (8)
(8)
从fa的计算式可以看出:当 时,
时, 。显然,这是不成立的。因此,Barton等[11]建议:在实际工程应用中,
。显然,这是不成立的。因此,Barton等[11]建议:在实际工程应用中, 不应该大于70°[13]。法向应力的极小值可用
不应该大于70°[13]。法向应力的极小值可用 =70°反算得:
=70°反算得:
 (9)
(9)
1.2 模型参数的关系分析
假设岩体的基本摩擦角为30°,变化JCS=5~105 MPa,JRC=0~18,根据上述推导,得到JRC和JCS的影响,分别见图1和图2。从图1可见:黏结力c和内摩擦角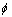 随JRC的增大而呈非线性增大;c与JRC关系曲线的斜率随JRC的增大而逐渐增大;
随JRC的增大而呈非线性增大;c与JRC关系曲线的斜率随JRC的增大而逐渐增大;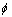 与JRC关系曲线的斜率随JRC的增大而逐渐减小。从JRC对内摩擦角的影响曲线(图1(b))可以看出:随着岩体压缩强度的增大,相同的JRC对应的内摩擦角也越大;对于相同增量JCS,随着JRC的增大,内摩擦角的增量也越来越大;而对于相同的JRC,随着JCS增大,内摩擦角的变化幅度却越来越小,说明JRC对于内摩擦角的影响大于JCS对于内摩擦角的影响。从图2可见:黏结力c随JCS的增大呈线性增大,而内摩擦角
与JRC关系曲线的斜率随JRC的增大而逐渐减小。从JRC对内摩擦角的影响曲线(图1(b))可以看出:随着岩体压缩强度的增大,相同的JRC对应的内摩擦角也越大;对于相同增量JCS,随着JRC的增大,内摩擦角的增量也越来越大;而对于相同的JRC,随着JCS增大,内摩擦角的变化幅度却越来越小,说明JRC对于内摩擦角的影响大于JCS对于内摩擦角的影响。从图2可见:黏结力c随JCS的增大呈线性增大,而内摩擦角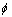 随JCS的增大而呈非线性增大。图2(a)显示:随着JRC的增大,JCS与黏结力的曲线的斜率也逐渐增大,说明在越粗糙的节理面下,JCS对于黏结力的影响越大。图2(b)显示:当JRC=0即节理面的平整度较高时,节理面的内摩擦角为基本摩擦角,均等于30°。
随JCS的增大而呈非线性增大。图2(a)显示:随着JRC的增大,JCS与黏结力的曲线的斜率也逐渐增大,说明在越粗糙的节理面下,JCS对于黏结力的影响越大。图2(b)显示:当JRC=0即节理面的平整度较高时,节理面的内摩擦角为基本摩擦角,均等于30°。

图1 JRC对黏结力和内摩擦角的影响
Fig.1 Effect of JRC on cohesion c and friction angle

图2 JCS对黏结力和内摩擦角的影响
Fig.2 Effect of JCS on cohesion c and friction angle
2 数值实现
2.1 数值计算方法
为了建立JRC-JCS模型中的数值计算方法,首先采用弹性增量理论,计算应力和变形情况的增量表达式[14]:
 (10a)
(10a)
 (10b)
(10b)
 (10c)
(10c)
式中: ;
; ;G为剪切模量;K为体积模量;
;G为剪切模量;K为体积模量; 为单元在i方向上的弹性应变增量。
为单元在i方向上的弹性应变增量。
通过弹性理论可得试算应力分量:
 ;i=1, 2, 3 (11)
;i=1, 2, 3 (11)
式中: 为初始应力;
为初始应力; 为应力增量。
为应力增量。
然后,根据塑性状态下的应变增量 为弹性应变增量
为弹性应变增量 和塑性应变增量
和塑性应变增量 之和,推导新的应力分量
之和,推导新的应力分量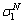 ,
,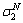 和
和 [14]:
[14]:
 (12)
(12)
 (13)
(13)
 (14)
(14)
联立式(10)~(14)得:
 (15)
(15)
 (16)
(16)
 (17)
(17)
 (18)
(18)
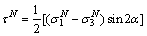 (19)
(19)
式中: 和
和 分别为计算更新的正应力和剪应力;
分别为计算更新的正应力和剪应力; 为节理面法向与
为节理面法向与 的夹角。
的夹角。
若应力点位于屈服面上,则满足下式:
 (20)
(20)
2.2 数值方法验证
采用VC++语言对FLAC3D软件数值计算模块进行二次开发,根据前面的数值计算方法编制相应程序。在计算过程中,根据弹性理论计算各个单元的应变及应力,然后,代入JRC-JCS模型进行判断,若达到屈服条件,则进行相应的应力调整,使应力满足屈服函数。为了验证程序的正确性,利用室内试验数据进行验证。通过室内节理剪切试验得到的节理剪切强度和正应力,如表1所示。JRC-JCS模型中节理粗糙系数JRC与节理粗糙形态有关,如图3所示。
利用室内节理面直接剪切试验结果,将数值计算结果与试验结果进行对比,如表1和图4所示。从表1和图4可见:试验结果得到的节理面剪切强度随正应力的增大而呈非线性增大,Mohr-Coulomb模型和JRC-JCS模型得到的结果与试验结果均较吻合;但当节理面正应力较小时,剪切强度的非线性特征较明显;Mohr-Coulomb模型无法描述该非线性特征,而JRC-JCS模型则可以较好地描述,并且JRC-JCS模型结果与试验结果的相关系数为0.991 50,高于Mohr-Coulomb模型的0.990 72,从而验证了JRC-JCS模型数值计算方法的可靠性。通过计算可得到JRC-JCS模型参数JRC=15.42,JCS=57.387 MPa;Mohr-Coulomb模型参数c=1.926 MPa,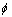 =33.45°。
=33.45°。
表1 数值模型的剪切强度
Table 1 Shear strength of numerical model MPa


图3 不同JRC对应的节理粗糙形态
Fig.3 Corresponding joint roughness morphologies with different JRC

图4 剪切强度计算结果与试验结果的比较
Fig.4 Comparison of shear strength for numerical calculation results and test results
2.3 参数影响分析
为了进一步研究JRC和JCS对于节理面剪切强度的影响,通过计算,固定 =2.0 MPa,得到JRC和JCS与节理面剪切强度的关系,分别如图5和图6所示。从图5和图6可以看出:随着JCS和JCS的增大,节理面的剪切强度均呈非线性增大;剪切强度与JRC的曲线斜率随JRC的增大而增大,而剪切强度与JCS的曲线斜率随JCS的增大而减小,即JRC的变化对于剪切强度的影响要比JCS的影响突出。
=2.0 MPa,得到JRC和JCS与节理面剪切强度的关系,分别如图5和图6所示。从图5和图6可以看出:随着JCS和JCS的增大,节理面的剪切强度均呈非线性增大;剪切强度与JRC的曲线斜率随JRC的增大而增大,而剪切强度与JCS的曲线斜率随JCS的增大而减小,即JRC的变化对于剪切强度的影响要比JCS的影响突出。

图5 JRC与节理面剪切强度的关系
Fig.5 Relation between JRC and shear strength of joint plane

图6 JCS与节理面剪切强度的关系
Fig.6 Relation between JCS and shear strength of joint plane
3 结论
(1) 通过理论推导,得到JRC-JCS模型参数与Mohr-Coulomb模型参数之间的关系,即黏结力c和内摩擦角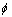 随JRC的增大而呈非线性增大;黏结力c随JCS的增大呈线性增大,而内摩擦角
随JRC的增大而呈非线性增大;黏结力c随JCS的增大呈线性增大,而内摩擦角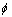 随JCS的增大而呈非线性增大。
随JCS的增大而呈非线性增大。
(2) 建立了基于JRC-JCS非线性强度模型的数值计算方法,并通过室内试验结果对数值方法进行了验证。研究了JRC和JCS对于节理剪切强度的影响,表明:随着JCS和JCS的增大,节理面的剪切强度均呈非线性增大;剪切强度与JRC的曲线斜率随JRC的增大而增大,而剪切强度与JCS的曲线斜率随JCS的增大而减小,即JRC的变化对于剪切强度的影响要比JCS的影响突出。
参考文献:
[1] 蒋青青, 胡毅夫, 赖伟明. 层状岩质边坡的遍布节理模型三维稳定性分析[J]. 岩土力学, 2009, 30(3): 712-716.
JIANG Qingqing, HU Yifu, LAI Weiming. Three dimensional stability analysis of stratified rock slope based on ubiquitous-joint model[J]. Rock and Soil Mechanics, 2009, 30(3): 712-716.
[2] 林杭, 曹平, 李江腾, 等. 层状岩质边坡破坏模式及稳定性的数值分析[J]. 岩土力学, 2010, 31(10): 3300-3304.
LIN Hang, CAO Ping, LI Jiangteng, et al. Numerical analysis of failure modes and stability of stratified rock slopes[J]. Rock and Soil Mechanics, 2010, 31(10): 3300-3304.
[3] Fraldi M, Guarracino F. Limit analysis of collapse mechanisms in cavities and tunnels according to the Hoek-Brown failure criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(4): 665-673.
[4] Li A J, Merifield R S, Lyamin A V. Stability charts for rock slopes based on the Hoek-Brown failure criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(5): 689-700.
[5] 巫德斌, 徐卫亚. 基于Hoek-Brown准则的边坡开挖岩体力学参数研究[J]. 河海大学学报, 2005, 33(1): 89-93.
WU Debin, XU Weiya. Hoek-Brown criterion-based study on mechanical parameters of excavated slope rock masses[J]. Journal of Hohai University, 2005, 33(1): 89-93.
[6] 林杭, 曹平, 赵延林, 等. 强度折减法在Hoek-Brown准则中的应用[J]. 中南大学学报: 自然科学版, 2007, 38(6): 1219-1224.
LIN Hang, CAO Ping, ZHAO Yanlin, et al. The application of strength reduction method in Hoek-Brown criterion[J]. Journal of Central South University: Science and Technology, 2007, 38(6): 1219-1224.
[7] 林杭, 曹平, 李江腾, 等. 基于广义Hoek-Brown准则的边坡安全系数间接解法[J]. 煤炭学报, 2008, 33(10): 1147-1151.
LIN Hang, CAO Ping, LI Jiangteng, et al. The indirect calculation method for the safety factor of slope based on generalized Hoek-Brown criterion[J]. Journal of China Coal Society, 2008, 33(10): 1147-1151.
[8] 蒋青青. 基于Hoek-Brown 准则点安全系数的边坡稳定性分析[J]. 中南大学学报: 自然科学版, 2009, 40(3): 786-790.
JIANG Qingqing. Stability of point safety factor of slope based on Hoek-Brown criterion[J]. Journal of Central South University: Science and Technology, 2009, 40(3): 786-790.
[9] 朱自强, 李海青, 柳群义, 等. 层状岩体结构面特征及其拟合描述模型[J]. 土木建筑与环境工程, 2009, 31(5): 38-42.
ZHU Ziqiang, LI Haiqing, LIU Qunyi, et al. Characteristics and fitting model of structure plane in layered rock mass[J]. Journal of Civil, Architectural & Environmental Engineering, 2009, 31(5): 38-42.
[10] Barton N, Pandey S K. Numerical modelling of two stoping methods in two Indian mines using degradation of c and mobilization of φ based on Q-parameters[J]. International Journal of Rock Mechanics & Mining Sciences, 2011, 48(7): 1095-1112.
[11] Barton N, Choubey V. The shear strength of rock joints in theory and practice[J]. Rock Mechanics, 1977(10): 1-54.
[12] Choi S O, Chung K. Stability analysis of jointed rock slopes with the Barton constitutive model in UDEC[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(S1): 581-586.
[13] 杜时贵, 郭霄, 颜育仁. JRC-JCS模型在抗剪强度参数取值中的应用[J]. 金华职业技术学院学报, 2004, 4(1): 1-4.
DU Shigui, GUO Xiao, YAN Yuren. JRC-JCS model and its application on studying shear strength of rock joint[J]. Journal of Jinhua College of Profession and Technology, 2004, 4(1): 1-4.
[14] Itasca Consulting Group. Theory and background[R]. Minnesota: Itasca Consulting Group, 2002: 35-78.
(编辑 陈灿华)
收稿日期:2012-08-12;修回日期:2012-10-20
基金项目:国家自然科学基金资助项目(50878212);四川省科技计划项目(2013JY0119);成都大学人才引进基金资助项目(2012年)
通信作者:吴启红(1981-),男,四川乐至人,博士,副教授,从事地质工程及岩土工程研究;电话:18628066800;E-mail: wqh1016@126.com