文章编号: 1004-0609(2005)06-0829-07
剪切变形方向特征对高纯铝箔轧制织构的影响
邓运来, 张新明, 唐建国, 刘 瑛, 陈志永, 周卓平
(中南大学 材料科学与工程学院, 长沙 410083)
摘 要: 运用取向分布函数(ODF)研究了每个轧制道次的剪切变形特征对高纯铝箔轧制织构的影响。 提出用中性角的相对大小来量化轧制剪切变形作用方向改变的位置, 运用Taylor晶体塑性变形理论模拟计算了中性角的相对大小对轧制织构演变的影响。 实测与模拟的轧制织构特征表明: 中性角靠近轧制变形区的中心位置有利于形成{001}〈110〉剪切织构, 从而证实了除剪切变形的程度外, 剪切变形方向改变的位置也是影响高纯铝箔轧制织构的重要因素。
关键词: 电容器; 高纯铝箔; 轧制织构; 中性角; 剪切变形; 织构模拟
中图分类号: TG111.7; TG115.22 文献标识码: A
Effect of direction change of shear deformation on
rolling textures in high purity Al foils
DENG Yun-lai, ZHANG Xin-ming, TANG Jian-guo, LIU Ying,
CHEN Zhi-yong, ZHOU Zhuo-ping
(School of Materials Science and Engineering,
Central South University, Changsha 410083, China)
Abstract: Effect of direction change of shear deformation on the rolling textures in high purity Al foils was investigated by orientation distribution function (ODF). The quantitative estimation of relative neutral angle was suggested and introduced into the Taylor-type crystal plasticity deformation model to simulate the rolling textures. It is shown that the condition of neutral angle locating at the middle point of rolling deformation zone favors the development of the {001}〈110〉 shear texture whatever the measured and the simulated ODFs are, which leads to the conclusion that the evolution of rolling textures is contributed by the parameter of relative neutral angle except the magnitude of shear deformation.
Key words: electrolytic capacitors; high purity Al foils; rolling textures; neutral angle; shear deformation; texture molding
Taylor晶体塑性变形理论以晶粒微观的应变(应变率)与样品宏观的协调为基本假设, 有两类晶体塑性变形模型, 晶粒微观塑性变形位移梯度张量的分量与样品宏观的完全相同时为FC模型; 允许晶粒微观塑性变形的剪切位移梯度分量中的一个或 几个与样品宏观的不完全相同时为RC模型[1-3]。 虽然文献[3-6]运用Taylor-Type模型, 对F.C.C.金属轧制织构演变及特点已作了描述, 但是样品宏观变形被简化成平面应变压缩(PSC, de33=-de11, de13=0。 其中, de33为轧向, de11为板横向, de13为板法向)模式, 忽略了轧制时样品宏观剪切变 形对轧制织构的影响。 事实上, 由于轧制几何与摩擦等边界条件的限制, 轧制过程中总是或多或少地存在剪切变形[7-10], Lee等[8]和Engler等[9]将轧制中性角假设在变形区沿轧向的中心点位置, 用de13和de31分别描述轧制几何与摩擦条件对轧制织构的影响, 发现由于轧制几何与摩擦作用引入的晶体转动效果正好相反, 考虑轧制剪切变形时, 作用在样品上的宏观位移梯度张量的分量可简化为: de33=-de11, de13≠0, 其他分量为0[9-10]。 在对电容器高纯铝箔织构演变的研究中发现[11-13]: 随轧制摩擦条件的改变, 轧制织构与变形微观组织发生了显著变化, 在强摩擦条件下, 不仅铝箔轧制织构中有{001}〈110〉剪切织构组分存在, 而且表层的形变剪切带中存在立方取向微区, 铝箔退火后得到了强立方织构。
本文作者旨在研究轧制剪切变形特征对高纯铝轧制织构的影响, 进而为探明铝箔中立方织构的形成机理提供有益的参考。
1 实验
每道次的轧制边界条件一般可以用轧辊与轧件的接触角(α)、 轧制摩擦角(β)和中性角(γ)来描述, 忽略张力的影响, α、 β和γ的关系满足:
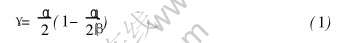
改变道次压下率r, α相应地改变, 由式(1)可知, 从而引起γ的变化, 而γ反映了轧制剪切变形改变方向的位置。 本实验采用高纯铝箔的两种轧制方案, 都以煤油作润滑剂, 摩擦角(β)由“轧制前滑实验”测定, 约为10°, 由于两种轧制方案的压下规程不同, 于是在轧制累计变形量(如∑ε11)相同时, 两种方案轧制过程中每道次的γ具有不同特征。 通过对比累计变形量相同时, 两种轧制方案样品的实测与Taylor-Type晶体塑性变形模型模拟计算的织构结果, 研究了每道次轧制剪切变形作用方向改变的位置(γ)对高纯铝轧制织构的影响。
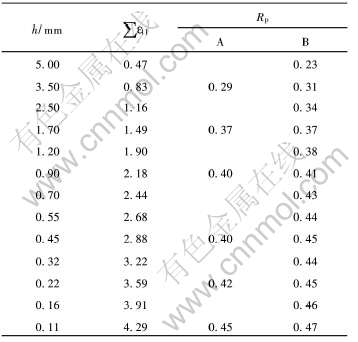
从一块含有弱的立方织构的高纯铝热轧板上截取2块尺寸为8.0mm×100mm×300mm的样品, 分别用两种方案(A和B)进行轧制, 厚度h=0.45mm和h=0.11mm(累计对数变形量分别为∑ε11=2.88和4.29)时取样测算样品织构, h=0.45mm时A和B方案的样品分别记为A1和B1, h=0.11mm时记为A2和B2。 两种方案均采用煤油作润滑剂, 方案A的道次变形量大于方案B的, 方案A的道次变形量r=48%~56%, 方案B的r=18%~38%, 详细情况列于表1。 方案A首先在轧辊半径R=200mm的轧机上将坯料轧至0.9mm, 随后在轧辊半径R=85mm的轧机上轧制; 方案B在轧辊半径R=85mm的轧机上完成。 表1中Rp为中性角与接触角的比值, 是相对中性角(RNA), 定义为:
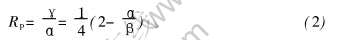
表1 高纯铝箔的轧制条件与参数
Table 1 Rolling parameters and conditions for high purity aluminum foils
每个样品测量了{111}、 {200}、 {220}、 {113}4个不完全极图, 运用球谐函数级数展开法求出l=22时取向分布函数(ODF)的C-系数[14]。 为消除“鬼峰”影响, 按Lücke等[15]提出的织构组份分析法计算出“真ODF”(l=23)。
2 实验结果
实际测算织构的“真ODF”用φ2为常数的典型截面(φ2=0°, 45°, 60°)表示, 如图1所示。 其中取向密度f(g)等高线水平范围为1~16。 从图1(a)和1(c)中可以看出, ∑ε11=2.88时, 轧制方案A、 B的样品(A1和B1)中都含有高层错能F.C.C金属PSC变形的典型织构组分, 在Euler空间中, 沿β-取向线从C-取向({112}〈111〉)经S-取向({123}〈634〉)到B-取向({011}〈211〉), 以及沿α-取向线的G-取向({011}〈100〉)和B-取向, α-和β-取向线交于B-取向; 但仅有方案B中沿=0°有取向聚集 的趋势。 而∑ε11=4.29时, 在方案A、 B的样品(A2和B2)中都出现了{001}〈110〉剪切织构, 但其强弱有明显的差别(图1(b)和图1(d))。
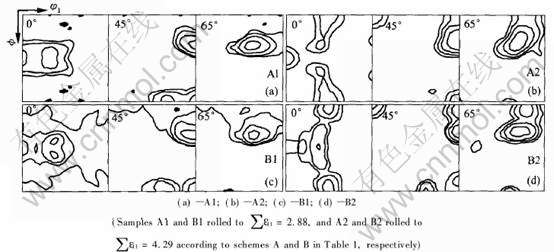
图1 样品实测的不同取向分布函数的截面(φ2=0°, 45°, 65°)
Fig.1 Sections(φ2=0°, 45°, 60°) of measured ODFs for samples
为了清楚地显示样品中的织构特征, 图2给出了样品实测织构的α、 β和γ-取向线上取向分布的情况。 从图2(a), 2(c)中可以看出, 当∑ε11达到2.88之后, 方案A和B中高纯铝轧制织构以β-取向线上C-织构、 S-织构组分为主, 但其值为27~30°, C-取向、 S-取向的f(g)与其在Euler空间的位置几乎是相同的, C-取向与其理想位置(90°, 35°, 45°)有一些偏离。 ∑ε11=2.88时, B-/S-过渡取向的f(g)最大, ∑ε11=4.29时, C-/S-过渡取向的f(g)最大。 随变形程度从∑ε11=2.88增加到4.29, C-、 C-/S-和{001}〈110〉 取向的f(g)增大, G-织构和B-织构减弱, B-织构减弱得比G-织构慢, 且B-取向有绕TD轴向减小的方向转动的趋势。
从图2(d)不难看出, ∑ε11=2.88时, A1样品的轧制织构中没有{001}〈110〉剪切织构组分, 即使∑ε11达到4.29, {001}〈110〉取向的f(g)也较小(约为2.3); 而方案B在∑ε11=2.88和4.29时, {001}〈110〉取向的f(g)分别为1.5和5.5。 当∑ε11相同时, 方案B样品的轧制织构中{001}〈110〉取向的f(g)要强于方案A的。
3 讨论
3.1 剪切变形特征影响轧制织构的分析方法
以轧制坐标系为参考坐标系, 假设轧制变形区的金属为平面变形, 宏观位移梯度张量为
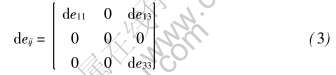
式中 de11为沿轧向的位移梯度分量; de33=-de11; de13为剪切位移梯度, 在轧制变形区(RDZ)内是变化的。 为了定量描述轧制剪切变形的大小, 定义:
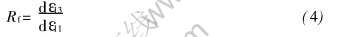
根据式(2)和(4)的定义, Rp为中性角的相对大小, 描述了剪切变形改变方向的位置; Rf为剪切应变与正应变增量的比值, 描述了单位轧向应变上沿轧向的剪切变形程度。
设一个轧制道次分成M步完成, 第k步对应RNA, 为了更加清楚地显示RNA的影响, 在前滑区和后滑区内, 假设同层金属在轧制前滑区和后滑区内每一加载步的Rf相同, 在一个轧制道中第n步的剪切位移梯度为
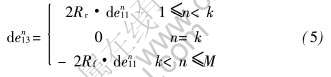
式(2)中的Rp可离散化为式(5)中的k, 通过式(5), 按照文献[5~6]介绍的计算方法, 可以在Taylor晶体塑性变形模型的框架内模拟计算不同特征的剪切变形对织构演变的影响。
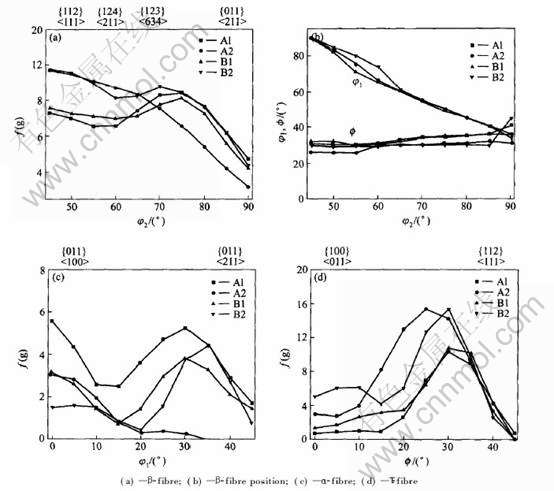
图2 实测织构的取向线
Fig.2 Skeleton lines of measured textures for samples A1, A2, B1 and B2 from Fig.1
3.2 轧制织构模拟计算结果
当累计变形量为∑ε11=2.88和4.29时, 计算出初始特征取向在Euler空间中的新位置, 假定其高斯分布半高宽为7°, 采用高斯函数分布表示“真ODF”(l=23), 由于轧件薄时直接测量Rf有一定的难度, 计算ODFs时, Rf被赋予不同的值。
通过织构模拟计算发现, 在Rf〈0.55时, 即使∑ε11=4.29, 方案A和B模拟的ODFs中仍未出现{001}〈110〉剪切织构。 Rf=0.55, Rp=γ/α时, 模拟计算的ODFs如图3所示, f(g)水平为1~62, SA1和SB1分别表示方案A和B在∑ε11=2.88时模拟计算的织构, SA2和SB2分别表示方案A和B在∑ε11=4.29时模拟计算的织构。
从图3中可以看出, ∑ε11=2.88时, SA1和SB1中并未出现{001}〈110〉剪切织构, 但方案B中, 沿=0°, 存在关于φ=45°对称分布的(0°, 25°, 0°)与(0°, 65°, 0°)取向, 有明显向φ=45°聚集的趋势。 ∑ε11=4.29时, SB2中(0°, 25°, 0°)与(0°, 65°, 0°)取向的f(g)小于1, 这些取向已转到了{001}〈110〉取向, SB1和SB2的轧制织构中都含有{001}〈110〉剪切织构组分, 且SB2的{001}〈110〉剪切织构明显强于SA2的。

图3 模拟计算的不同取向分布函数的截面(φ2=0°, 45°, 65°)
Fig.3 Sections(φ2=0°, 45°, 60°) of simulated ODFs under conditions of SA1 (a), SA2 (b), SB1(c), and SB2 (d), corresponding to samples A1, A2, B1 and B2 in Table 1, respectively
从模拟织构的α-、 β-和τ-取向线上取向分布的情况(图4)可以进一步看出, α-取向线上G-和B-取向的f(g)小于1。 随变形程度的增加, β-取向线上取向的值为27°~30°, C-与{001}〈110〉取向的f(g)升高, 过渡取向C-/S-(45°≤φ2≤65°)的f(g)也升高, 但过渡取向S-/B-(65°≤φ2≤85°)的f(g)降低, 值减小至27°。 另外, 在累计变形量相同时, 两种轧制方案中β-取向线在Euler空间中的位置基本上没有变化。
3.3 剪切变形特征对轧制织构的影响
从表1中方案A和B的轧制参数来看, ∑ε11累积到4.29时, 方案A的RNA偏离RDZ中点的程度要大于方案B的。 无论是实测还是模拟结果都表明, 由于剪切变形在轧制前滑区与后滑区改变作用方向, 如果RNA偏离了α/2位置, 则不一定形成强的{001}〈110〉剪切织构, 剪切变形恰好在α/2位置改变方向, 最有利于形成{001}〈110〉剪切织构组分。
本文模拟ODFs结果也表明, 轧制剪切变形的程度(Rf)对形成{001}〈110〉剪切织构也是相当重要的, 要形成{001}〈110〉剪切织构, Rf有一个临界值, 本文通过模拟与实验对照, 得到的结果为: Rf≥ 0.55, 此时只有RNA在RDZ中点才能在轧制织构中形成{001}〈110〉剪切织构组分。 上述实测与模拟计算的织构特征证实了高层错能FCC金属轧制织构中{001}〈110〉剪切织构组分的形成与两个参数Rp和Rf有关。
最后需指出的是, 尽管考虑了两个参数Rp与Rf对高纯铝轧制织构的影响, 模拟计算的织构特征接近于实测结果, 但模拟与实测ODFs中取向的f(g)在数量上仍然有差距。 除了文献[4-6]指出的原因外, 可能与模拟计算时所有晶粒都受到了相同的Rf作用, 没有考虑其在厚度方向上的变化也有关。
4 结论
提出了一个简便地描述轧制剪切变形特征影响轧制织构的方案: 用量Rp=γ/α化剪切变形改变方向的位置, Rf=dε13/dε11描述剪变形的程度。 将Rf、 Rp输入到Taylor-Type晶体塑性变形模型中模拟计算与实测织构特征进行了比较, 得到如下结论。
1) 样品实测织构的β-取向线上聚积取向的约为27°~30°, 随变形程度的增加, C-、 C-/S-织构增强; S-/B-织构, α-取向线上G-和B-织构减弱, {001}〈110〉剪切织构的形成明显受到每道次中性角相对大小的影响。
2) 用提出的Rp=γ/α量化每个轧制道次剪切变形作用方向改变的位置, 采用Taylor-Type晶体塑性变形模型模拟计算的轧制织构特征与实测结果符合较好。
3) 轧制织构中{001}〈110〉 剪切织构组分的形 成与两个参数Rf和Rp有关, 中性角越接近α/2, 越利于形成{001}〈110〉剪切织构。

图4 模拟计算的取向线
Fig.4 Skeleton lines of simulated textures under conditions of SA1, SA2, SB1 and SB2 from Fig.3
REFERENCES
[1]Taylor G I. Plastic strain in metals[J]. J Inst Met, 1938, 62: 307-324.
[2]Honneff H, Mecking H. A method of the determination of the active slip systems and orientation changes during single crystal deformation[A]. Proc ICOTOM 5[C]. Aache: Springer-Verlag, 1978. 265-275.
[3]Sevillano J G, von Houtte P, Aernoudt E. Large strain work hardening and texture[J]. Prog Mater Sci, 1980, 25: 69-412.
[4]Hirsch J, Lücke K. Mechanism of deformation and development of rolling textures in polycrystalline F.C.C. metals(Ⅱ)—simulation and interpretation of experiments on the basis of taylor-type theories[J]. Acta Metall, 1988, 36(11): 2883-2904.
[5]CHEN Zhi-yong, ZHANG Xin-ming, ZHOU Zhou-ping, et al. Simulation of rolling texture of aluminum with lath model[J]. Trans Nonferrous Met Soc China, 1999, 9(2): 307-311.
[6]Chen Z Y, Zhang X M, Du Y, et al. Taylor-type simulation of the rolling texture of pure aluminum taking into account the initial texture[J]. Mater Sci Forum, 2002, 408-412: 475-480.
[7]Truszkowski W, Krol J, Major B. On penetration of shear texture into the rolled aluminum and copper[J]. Metall Trans A, 1982, 13A: 665-669.
[8]Lee C S, Duggan B J. A simple theory for the development of inhomogeneous rolling textures[J]. Metall Trans A, 1991, 22A: 2637-2643.
[9]Engler O, Huh M Y, Tome C N. A study of through-thickness texture gradients in rolled sheets[J]. Metall and Mater Trans A, 2000, 31A: 2299-2315.
[10]Pérocheau F, Driver J H. Texture gradient simulations for extrusion and reversible rolling of FCC metals[J]. International Journal of Plasticity, 2000, 16: 73-89.
[11]张新明, 蒋红辉, 肖亚庆, 等. 润滑剂对高纯铝形变织构的影响[J]. 中国有色金属学报, 2001, 11(5): 785-790.
ZHANG Xin-ming, JIANG Hong-hui, XIAO Ya-qing, et al. Influence of lubricants on deformation texture in high purity Al[J]. The Chinese Journal of Nonferrous Metals, 2001, 11(5): 785-790.
[12]Zhang X M, Xiao Y Q, Jiang H H, et al, Cube recrystallization texture in high-purity aluminum foils rolled with different lubrication[A]. Gottstein G, Molodov D A. Recrystallization and Growth Proceed- ings of the First Joint International Conference[C]. RWTH-Aachen: Springer, 2001. 1335-1340.
[13]邓运来, 张新明, 刘瑛, 等. 几何因素与摩擦耦合对高纯铝箔剪切织构的影响[J]. 中国有色金属学报, 2002, 12(4): 634-638.
DENG Yun-lai, ZHANG Xin-ming, LIU Ying, et al. Effect of geometry of deformation and friction on shear texture in high purity aluminum foils[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(4): 634-638.
[14]Bunge H J. Mathematische Methoden der Texturanalyse[M]. Berlin: Akademie Verlag, 1969. 4-6.
[15]Lücke K, Pospiech J, Virnich K H, et al. On the problem of the reproduction of the true orientation distribution from pole figures[J]. Acta Metall, 1981, 29: 167-185.
(编辑陈爱华)
基金项目: 国家自然科学基金资助项目(50231030; 50301016); 国家教育部博士点基金资助项目(2004053304)
收稿日期: 2004-10-08; 修订日期: 2004-12-27
作者简介: 邓运来(1969-), 男, 副教授, 博士研究生.
通讯作者: 邓运来, 副教授; 电话: 0731-8830265; E-mail:luckdeng@mail.csu.edu.cn