浅表层及粗晶材料缺陷超声诊断方法
闫晓玲1, 2,董世运2,徐滨士2,潘亮2,王望龙2
(1. 北京理工大学 机械与车辆学院,北京,100081;
2. 装甲兵工程学院 装备再制造技术国防科技重点实验室,北京,100072)
摘要:针对浅表层及粗晶材料,提出一种用小波变换与广义相关倒频谱分析相结合的缺陷诊断方法。该方法利用小波多分辨特性去除白噪声,利用广义相关倒频谱剔除始脉冲及材料散射噪声。实验结果表明:该方法提高了对浅表层及低信噪比缺陷的分辨力,缺陷诊断结果与实际结果相吻合,可用于浅表层及粗晶材料缺陷的诊断。
关键词:浅表层;粗晶材料;小波变换;相关倒频谱;缺陷诊断
中图分类号:TM343;TP277 文献标志码:A 文章编号:1672-7207(2013)07-2751-05
Ultrasonic detection method for shallow and coarse-grained material fault
YAN Xiaoling1, 2, DONG Shiyun2, XU Binshi2, PAN Liang2, WANG Wanglong2
(1. School of Mechanical Engineering,Beijing Institute of Technology, Beijing 100081, China;
2. Science and Technology on Remanufacturing Laboratory, Academy of Armored Forces Engineering, Beijing 100072, China)
Abstract: A new diagnosis method by using wavelet transform and the generalized correlation cepstrum was introduced for shallow and coarse-grained materials. The wavelet for multi-resolution analysis was used to suppress the white noise, and the generalized correlation cepstrum excluded the impact of Initial pulse and material scattered noise. The experimental results show that the resolution of shallow and low SNR faults is improved by the method using wavelet transform and the generalized correlation cepstrum. The fault diagnosis results are consistent with the actual results, so the method can be used for the diagnosis of shallow and low SNR faults.
Key words: shallow; coarse-grained material; wavelet transform; relevant cepstrum; fault diagnosis
再制造是将大量同类报废产品回收,利用高新技术对其进行批量化修复,使产品技术性能和质量都能达到甚至超过原机新品的水平,以最小的投入获得最大的经济效益。再制造产品的质量控制是再制造工程的核心,由于表面工程技术的发展,产品的表面质量一般能够保证。产品质量控制和寿命评估的关键是检测浅表层和内部缺陷。利用超声波信号对零部件或材料内部缺陷进行检测是无损检测技术中的一种有效手段[1-4]。在超声波检测中,无论是探测零件表层及内部缺陷,还是对材料组织结构表征和性能评价,超声波回波信号都非常重要。一方面,超声回波信号中携带了大量与材料特性有关的丰富信息;另一方面,超声波回波信号会受到仪器、探头、耦合、被测材料等多方面因素的影响。当缺陷位于浅表层时,由于探伤仪阻塞时间和始脉冲宽度的影响,存在着检测盲区(盲区是指从探测面到能够发现缺陷的最小距离,表征系统的近距离分辨能力)。当材料晶粒比较粗大时,散射衰减比较严重,被散射的超声波传播到探头,在示波屏上引起林状回波(又叫草波),使信噪比下降,严重时甚至会淹没缺陷波。为此,本文作者运用小波变换与广义相关倒频谱分析方法,以提高对浅表层及低信噪比缺陷的分辨力,实现对再制造零件质量的有效监控。
1 脉冲反射法探伤原理
脉冲反射法是目前运用最广泛的一种超声波探伤法。当超声波遇到由声阻抗不同的介质构成的界面时,将会发生反射现象。采用1个探头兼作发射和接收器件,接收信号在探伤仪的荧光屏上显示,并根据缺陷及底面发射波来判断缺陷。脉冲反射法检测原理如图1所示。
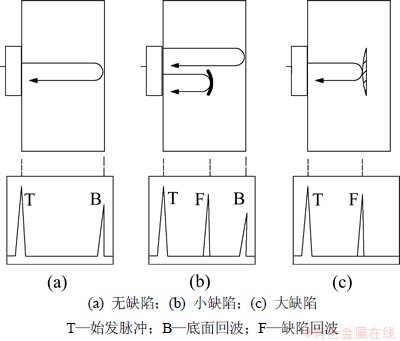
图1 脉冲反射法检测原理
Fig.1 Testing principle of pulse reflection method
超声检测信号中通常混杂有不同程度且种类各异的噪声,给材料的缺陷识别和特征表征带来困难。超声波检测信号中的噪声可分声学噪声和非声学噪声两大类。声学噪声来源于介质内部不同阻抗界面上的反射、折射和散射,反映的是介质的微观结构。非声学噪声主要包括电子电路噪声、脉冲噪声等,来源于仪器电路、模数转换过程等外部检测条件和环境。2类噪声之间有本质区别,分析和处理方式也不同。Shanker等[1-2]研究表明:声学噪声在部分时间区间上与缺陷回波信号相关,采用常用的信号处理方法,如信号平均技术、滤波技术、小波变换等去噪效果不是很理想。作者采用广义相关倒频谱分析方法有效消除了此类噪声,同时提高了对浅表层缺陷的分辨力。一般认为非声学噪声是白噪声,与缺陷回波信号不相关,在整个观测时域内服从均值为0、方差为σ的高斯分布,采用小波变换能够实现缺陷信号与非声学噪声的近似最优分离[3-4]。
2 小波分析
小波分析属于时频分析的一种,它具有多分辨率及其良好的局部特性,是分析非平稳信号的强有力工具。为了实现对白噪声的有效去除,利用正交小波基symmlet-8(具有紧致性、正则性、对称性,与缺陷回波相似)将超声波信号分解为不同尺度下的各个分量。
每次分解产生低频近似分量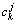 和高频细节分量
和高频细节分量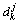 ,由于信号的细节和噪声包含在
,由于信号的细节和噪声包含在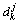 中,因此,下一次只对
中,因此,下一次只对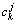 进行分解。多分辨分析公式如下:
进行分解。多分辨分析公式如下:
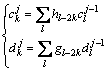 (1)
(1)
式中: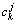 和
和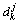 表示第j层第k个近似分量和细节分量小波系数;
表示第j层第k个近似分量和细节分量小波系数;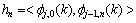 相当于低通波器组,分解出低频系数
相当于低通波器组,分解出低频系数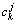 ;
;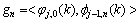 相当于高通滤波器组,分解出高频系数
相当于高通滤波器组,分解出高频系数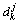 ;
;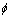 和
和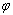 分别为尺度函数和小波函数。
分别为尺度函数和小波函数。
采用上述方法可以将超声波信号按任意时频分辨率分解,随着分解层数的增加,噪声的能量会迅速衰减,主要体现在噪声分解的小波系数越来越小,只有根据小波分解系数的变化选择自适应的阈值,才能达到有效去除噪声的目的。Donoho阈值[5]不仅考虑了白噪声的统计学分布(高斯分布)特征,也体现了噪声在不同分解尺度之间的差异,因此,在小波分解高频系数上作用Donoho阈值算子,能够实现缺陷信号与白噪声的近似最优分离。Donoho阈值为
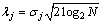 (2)
(2)
式中: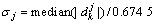 ,
,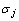 为第j层细节分量小波系数的噪声方差;N为信号采样点数。
为第j层细节分量小波系数的噪声方差;N为信号采样点数。
根据滤波后的近似分量和细节分量可以实现对信号s的重构,重构方法如下:
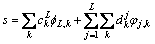 (3)
(3)
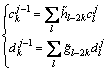 (4)
(4)
式中: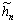 和
和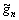 分别为hn和gn对应共轭滤波器组。
分别为hn和gn对应共轭滤波器组。
3 广义相关倒频谱分析
倒频谱分析也称二次频谱分析技术,是现代信号处理科学中的一项新技术,它可以提供FFT频谱图上难以捕捉的信息。倒频谱分析包括功率倒谱分析和复倒谱分析2种主要形式[6-7]。复数倒谱分析的定义为“信号序列z变换的对数傅里叶逆变换”,其表达式为:
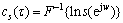
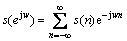 (5)
(5)
式中,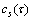 为复数倒频谱,单位为dB;F-1为傅里叶逆变换;自变量τ称为倒频率。本文采用广义相关倒谱分析,即
为复数倒频谱,单位为dB;F-1为傅里叶逆变换;自变量τ称为倒频率。本文采用广义相关倒谱分析,即
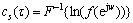 (6)
(6)
式中: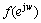 为频域信号,可通过多种方式获得,如频域信号的滤波、数学运算等,且
为频域信号,可通过多种方式获得,如频域信号的滤波、数学运算等,且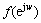 不再局限于一种信号,可以是多种信号的组合。对去除白噪声的超声波信号进行广义相关倒频谱分析,可以实现对对浅表层及低信噪比缺陷的诊断,其原因可以从以下几方面进行分析。
不再局限于一种信号,可以是多种信号的组合。对去除白噪声的超声波信号进行广义相关倒频谱分析,可以实现对对浅表层及低信噪比缺陷的诊断,其原因可以从以下几方面进行分析。
(1) 从超声波检测信号的特点进行分析。在适当的假设条件下,脉冲反射法超声检测系统中各个组成部分都可以模拟成一个线性非时变系统[8-9],如图2所示,每个线性非时变系统的属性都分别由时域中的单位冲击响应函数(上侧)和频域中单位冲击响应函数的频谱(下侧)来表征。通过这一系列的线性非时变系统,用来激发超声波的电压信号就会转化为最终在示波屏上显示的包含有用信息的电压输出信号。可见:由脉冲发生器产生的输入电压信号si(t)经过一系列信号转化过程,最终得到超声探伤仪示波器上显示的输出电压信号so(t)。这个过程在时域中可表示为
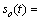
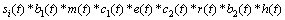 (7)
(7)
上述过程的频域表达式为
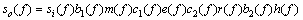 (8)
(8)
因此,最终超声探伤仪示波器上显示的输出电压信号包含除了输入电压信号、缺陷回波信号、底波回波信号之外其他不相关系统的影响。这些影响有的取决于脉冲发生器、接收器和超声换能器的参数设定,有的取决于被检测材料的性质,因此,表征整个系统属性时,必须考虑这些因素。可以将这些因素统称为检测系统的影响因素。由式(8)可知,缺陷的单位冲击响应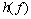 唯一确定缺陷的性质,
唯一确定缺陷的性质,
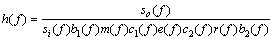 (9)
(9)
式(9)中的分母代表的是没有缺陷情况下材料的输出响应。由于再制造主要是对大量同类报废产品回收,利用高新技术对其进行批量化修复,因此,在同样实验条件下,采集同类产品中无缺陷情况下的超声波检测信号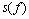 作为基准信号,对实际检测信号在频域进行归一化处理,可以剔除检测系统的影响,提高对近距离及低信噪比缺陷的分辨力。这是因为超声波检测盲区主要取决于探伤仪阻塞时间和始脉冲宽度,减小始脉冲宽度可以缩小探伤盲区,但探伤的灵敏度会降低[10-11]。采取上述信号处理方法剔除了始脉冲的影响,因此,可以发现始脉冲宽度以内的缺陷,并且不会降低探伤的灵敏度。低信噪比信号主要是材料散射衰减引起的,上述方法也剔除了材料散射衰减的影响,因而能够提高信噪比。
作为基准信号,对实际检测信号在频域进行归一化处理,可以剔除检测系统的影响,提高对近距离及低信噪比缺陷的分辨力。这是因为超声波检测盲区主要取决于探伤仪阻塞时间和始脉冲宽度,减小始脉冲宽度可以缩小探伤盲区,但探伤的灵敏度会降低[10-11]。采取上述信号处理方法剔除了始脉冲的影响,因此,可以发现始脉冲宽度以内的缺陷,并且不会降低探伤的灵敏度。低信噪比信号主要是材料散射衰减引起的,上述方法也剔除了材料散射衰减的影响,因而能够提高信噪比。

图2 一系列线性非时变系统组成的NDE系统
Fig.2 A series of linear time-invariant system consisting of NDE system
(2) 从倒频谱分析的特点分析。倒频谱实际上是频域信号取对数的傅里叶逆变换再处理,取对数的目的是为了使再变换后信号的能量更加集中。对信号做倒频谱分析,给信号频谱中的低幅值分量有较高的加权,可以帮助判别谱的周期性,又能精确地测出频率的间隔。所以,对实际检测信号在频域进行归一化处理,获得表征缺陷性质的单位冲击响应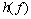 ,然后,对
,然后,对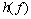 作倒频谱分析(式(10)所示),能够提高对低信噪比缺陷的辨别力。
作倒频谱分析(式(10)所示),能够提高对低信噪比缺陷的辨别力。
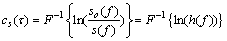 (10)
(10)
4 实验研究
为了验证基于小波变换变换和广义相关倒谱分析技术的有效性,对铸铁材料试样内部缺陷进行实验研究。在试样内部预制1个人工孔。超声探头采用直径为20 mm、频率2.5 MHz水浸点聚焦探头,采用反射式探测,采样频率为100 MHz。图3所示为铸铁材料试样的A型超声波检测信号,图中a为信号幅值(单位为V),t为时间(单位为μs)。从图3可以看出,始发脉冲和底面回波比较明显,但是由于材料散射衰减和白噪声的影响,缺陷回波基本看不出来。图4所示为小波分析处理的结果。从图4可以看出,白噪声已被消除,但是,材料散射噪声依然较明显,仍然无法准确辨别缺陷回波位置。图5所示为采集到的无缺陷铸铁试样的超声波检测信号,此信号作为基准信号。图6所示为采用小波分析和广义相关倒频谱分析的结果。从图6可以看出:3个缺陷回波分别位于10,15和20 μs处,根据超声波在铸铁中的传播速度v=4 146 m/s,计算3个缺陷与探头所在平面的距离分别为4.146,6.220和8.830 mm,计算结果与实际缺陷位置十分吻合,最大误差仅0.16 mm。另外,3个缺陷回波幅值与实际缺陷也吻合(20 μm处人工孔最大,10 μm处人工孔次之,15 μm处人工孔最小)。根据距离-波幅-缺陷当量曲线(AVG曲线)即可确定缺陷的当量尺寸。
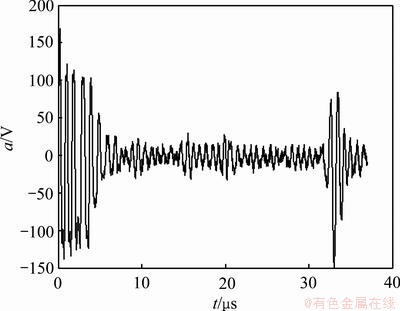
图3 铸铁试样超声波检测信号
Fig.3 Ultrasonic detection signal of iron sample
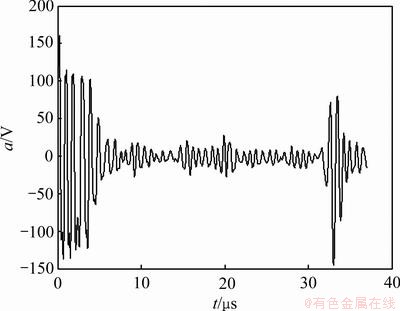
图4 小波变换消噪后的信号
Fig.4 Denoising result of ultrasonic detection signal based on wavelet transform
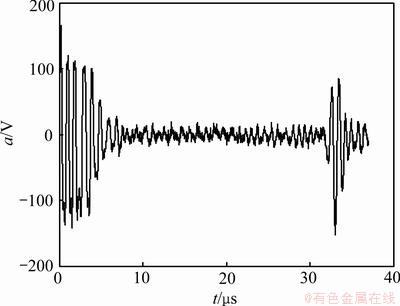
图5 无缺陷铸铁试样超声波检测信号
Fig.5 Ultrasonic detection signal of iron sample without flaw
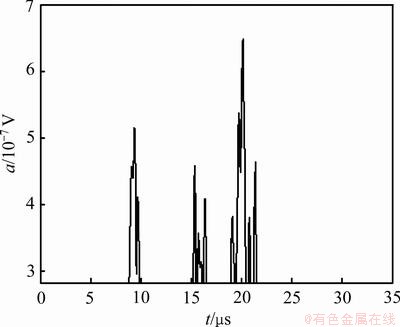
图6 基于小波变换和相关倒频谱分析的信号
Fig.6 Ultrasonic detection signal based on wavelet transform and relevant cepstrum
5 结论
(1) 针对浅表层及粗晶材料零件内部缺陷超声波检测信号的特点,提出了基于小波变换与广义相关倒谱相结合的缺陷诊断方法。
(2) 小波变换能够实现非声学噪声(在整个观测时域内服从均值为0、方差为σ的高斯分布)与缺陷信号的近似最优分离。广义相关倒谱分析能够剔除始脉冲和材料散射衰减的影响,提高对浅表层及低信噪比缺陷的分辨力。
(3) 缺陷诊断结果与实际结果相吻合,表明基于小波变换与广义相关倒谱相结合的缺陷诊断方法可用于实际缺陷的诊断。
参考文献:
[1] Shanker K, Rose M. Split spectrum processing determination of the available bandwidth for spectral splitting[J]. Ulrasonics, 1988, 26(7): 204-208.
[2] Ykhlef F, Arezki M. A wavelet denosing method to improve detection with ultrasonic signal[C]// IEEE International Conference on Industrial Technology. Piscataway: IEEE Computer Society Press, 2004: 1422-1425.
[3] Nikolaou N G. Rolling element bearing fault diagnosis using wavelet packets[J]. NDT&E International, 2002, 35(3): 197-205.
[4] 刘守山, 杨辰龙. 基于自适应小波阈值的超声信号消噪[J]. 浙江大学学报: 工学版, 2007, 41(9): 1557-1561.
LIU Shoushan, YANG Chenlong. Adaptive wavelet thresholding based ultrasonic signal denoising[J]. Journal of Zhejiang University: Engineering Science, 2007, 41(9): 1557-1561.
[5] Donoho D L. De-noising by soft threshold[J]. IEEE Transaction on Information Theory, 1995, 41(3): 617-627.
[6] 胡昌华, 李国华. 基于MATLAB6.x的系统分析与设计[M]. 西安: 西安电子科技大学出版社, 2003: 150-160.
HU Changhua, LI Guohua. Design and system analysis based on MATLAB[M]. Xi’an: Xidian University Press, 2003: 150-160.
[7] 华容. 信号分析与处理[M]. 北京: 高等教育出版社, 2004: 95-99.
HUA Rong. Signal analysis and processing[M]. Beijing: Higher Education Press, 2004: 95-99.
[8] Saniie J, Nagle D T, Donohue K D. Analysis of order statistic filters applied to ultrasonic flaw detection using split spectrum processing[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 1991, 38(2): 133-140.
[9] Lester W, Schmerr J, Sung J S. Ultrasonic nondestructive evaluation systems:models and measurements[M]. New York: Springer, 2007: 32-38.
[10] Lester W, Schmerr J. Fundamentals of ultrasonic nondestructive evaluation: a modeling approach[M]. New York: Plenum Press, 1998: 30-38.
[11] 林莉, 李喜梦. 超声波频谱分析技术及应用[M]. 北京: 机械工业出版社, 2009: 172-179.
LIN Li, LI Ximeng. Ultrasonic spectrum analysis technology and its application[M]. Beijing: Mechanical Industry Press, 2009: 172-179.
(编辑 赵俊)
收稿日期:2012-08-26;修回日期:2012-11-02
基金项目:国家自然科学基金资助项目(50975287);国家重点基础研究发展计划(“973”计划)项目(2011CB013405)
通信作者:董世运(1973-),男,山东菏泽人,博士,教授,从事激光熔覆及超声波无损检测研究;电话:13581967395;E-mail: syd422@vip.Sohu.com