Real-time routing control design for traffic networks with multi-route choices
来源期刊:中南大学学报(英文版)2016年第7期
论文作者:罗莉华 葛颖恩 陈继红 张方伟
文章页码:1807 - 1816
Key words:real-time VMS-based routing control; multi-route choices; model predictive control (MPC); system optimum; drivers’ acceptability
Abstract: This work considers those road networks in which there are multi-route choices for bifurcation-destination (or origin-destination) pairs, and designs a real-time variable message sign (VMS)-based routing control strategy in the model predictive control (MPC) framework. The VMS route recommendation provided by the traffic management authority is directly considered as the control variable, and the routing control model is established, in which a multi-dimensional control vector is introduced to describe the influence of route recommendations on flow distribution. In the MPC framework, a system optimum routing strategy with the constraints regarding drivers’ acceptability with recommended routes is designed, which can not only meet the traffic management authority’s control requirement but also improve drivers’ satisfaction with the route guidance system. The simulation carried out shows that the proposed routing control can effectively mitigate traffic congestion, reduces followers’ time delay, and improves drivers’ satisfaction with routing control in road networks.
J. Cent. South Univ. (2016) 23: 1807-1816
DOI: 10.1007/s11771-016-3234-6

LUO Li-hua(罗莉华), GE Ying-en(葛颖恩), CHEN Ji-hong(陈继红), ZHANG Fang-wei(张方伟)
College of Transport and Communications, Shanghai Maritime University, Shanghai 201306, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: This work considers those road networks in which there are multi-route choices for bifurcation-destination (or origin-destination) pairs, and designs a real-time variable message sign (VMS)-based routing control strategy in the model predictive control (MPC) framework. The VMS route recommendation provided by the traffic management authority is directly considered as the control variable, and the routing control model is established, in which a multi-dimensional control vector is introduced to describe the influence of route recommendations on flow distribution. In the MPC framework, a system optimum routing strategy with the constraints regarding drivers’ acceptability with recommended routes is designed, which can not only meet the traffic management authority’s control requirement but also improve drivers’ satisfaction with the route guidance system. The simulation carried out shows that the proposed routing control can effectively mitigate traffic congestion, reduces followers’ time delay, and improves drivers’ satisfaction with routing control in road networks.
Key words: real-time VMS-based routing control; multi-route choices; model predictive control (MPC); system optimum; drivers’ acceptability
1 Introduction
Traffic congestion is a serious problem all over the world, and several traffic control approaches, such as route guidance, ramp metering and variable speed limit have been designed to alleviate it and improve the operations of traffic flow [1-3]. In a traffic route guidance system, information (i.e. accidents, road blocked, estimated travel time) or route recommendation either through variable message signs (VMS), in-vehicle devices or other actuators, is provided to drivers, in order to influence their route-choice behavior and relieve overloaded routes by redirecting the flow to the routes with spare capacity [4-6]. In recent years, real-time routing control based on VMS, which provides the route recommendations towards a certain destination, has been widely applied in motorways or urban arterials [7].
In the route guidance system, the influence of drivers’ route choice can be projected to the splitting rates at the bifurcation node, and therefore, the bifurcation splitting rates are usually considered as the control variables (decision variables) in the routing controller design. For example, KOTSIALOS et al [5] proposed the routing strategy based on nonlinear optimal control theory; WANG et al [8] designed the feedback route guidance strategy; XU et al [9] utilized the model predictive control framework for the route guidance system; in order to deal with the difficulty in estimating the travel time, a diversion strategy was proposed based on the traffic condition [10]. However, bifurcation splitting rates are uncontrollable directly by the traffic management authority and are determined by the drivers themselves in real implementation. In the VMS-based route guidance system, what can actually be controlled are when and what kind of route recommendation is provided via VMS. Therefore, the VMS route recommendation provided by the traffic management authority, rather than the bifurcation splitting rate, is directly considered as the control variable in this paper, which is helpful to provide practical guidance for the traffic management authority designing the routing control strategy.
In the existing literature, the two-route diversion control has been studied a lot, e.g., one primary route and one secondary route, for the bifurcation-destination (BD) pair or origin-destination (OD) pair. While in reality, there may exist more than two alternative route choices, which include the freeways and surface roads, for the BD or OD pair [11], and if accidents or congestions occur on the freeways, the traffic management authority will often direct the traffic from the freeways to the surface roads with sufficient spare capacity. To avoid shifting the congestion from the freeways to the surface roads, dynamic routing strategies are required to direct the traffic in an orderly way, and if necessary, the traffic signal control on the surface roads is adapted [12]. In order to design the routing control strategy for the multi-route choices network, the influence of provided route recommendation (control variable) on the flow distribution at each alternative route should be described, and the traditional one-dimensional routing control variable (i.e., the control variable is defined to be 1 if the primary route is recommended, and 0 if the alternative route is recommended) is incapable to handle this problem. In this work, the routing control design for the multi-route choices network is discussed.
Generally, the routing control strategy is designed to reach either system optimum (SO) [5, 9] or user equilibrium (UE) [8, 10]. From the aspect of traffic management authority, the objective of route guidance should be the minimization of the total travel time for all the vehicles in network, in order to reach SO and improve network efficiency. The SO-based routing is accordant with the requirement of traffic management authority, but it will lead some followers to the unacceptable long time routes, so it may cause distrust and rejection of VMS recommendation after a long practical run. The UE-based routing is to equalize the travel time of all the utilized routes, and it will be more acceptable to drivers without sacrificing their benefits, but it behaves worse in the network performance. In order to satisfy both the traffic management authority’s control objective and drivers’ demand, a route guidance strategy was designed, in which the system optimum was considered as the control objective, and the constraint regarding user optimum was introduced to guarantee that nobody who follows the route recommendations is disadvantaged compared to the non-followers [13]. The constraint is demanding (strict) for the traffic management authority, since there is generally only one fastest route (the equilibrium state is not included) for the BD or OD pair, and the constraint will solely determine the recommended route (control variable). Actually, drivers cannot accurately forecast the shortest travel time for the BD or OD pair, and the slight time delay caused by following the route guidance is tolerant or even cannot be perceived. Therefore, the relaxation of the constraint regarding drivers’ requirement is considered, and a system optimum routing strategy is designed since the traffic management authority is in the dominant position in the route guidance system.
In this work, the real-time VMS-based routing control strategy for the multi-route choices is designed. Model predictive control (MPC) framework is utilized for the controller design, to perform robust with regard to system disturbances and uncertainties [14-15]. The routing control model is established, in which the multi-dimensional control vector is introduced to describe the influence of provided route recommendations on the flow distribution at each alternative route. In MPC framework, the routing control strategy will be finally transformed to an online nonlinear integer programming (NIP), and the dual-loop searching algorithm based on Tabu-Search (TS) with parallel computing is developed to solve it. The simulation results verify the proposed routing control strategy.
2 Traffic flow model
For the routing control design, the macroscopic traffic flow model is required to describe the traffic flow from a global perspective [16-18]. The validated macroscopic model, METANET [19], is considered, since it is proper for the design of route guidance control [5]. In the METANET model, both the time and space arguments are discretized. A motorway network is composed of nodes (bifurcations, junctions, and on/off ramps) and links (stretches between nodes). Each link m is assumed to have uniform characteristics, and it’s divided into Nm segments with equal length.
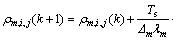
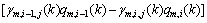 (1)
(1)
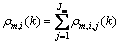 (2)
(2)
 (3)
(3)

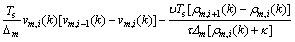 (4)
(4)
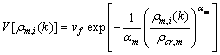 (5)
(5)
where Ts refers to the sampling time period of discretization; ρm,i(k) and vm,i(k) refer to the mean density, space-mean velocity at time kTs, respectively; qmj(k) refers to the traffic volume for segment i in link m during the period [kTs, (k+1)Ts]; ρm,i,j represents the partial density of ρm,i, which is destined to j; γm,i,j is the portion of qm,i that is destined to j; and Jm refers to the set of destinations that can be reachable by link m; △m and λm represent the segment length and the number of lanes for link m, respectively; vf refers to the free speed; ρcr,m is the critical density; αm, τ,  and κ are the model parameters depending on the road geometry, vehicle characteristics, and etc.
and κ are the model parameters depending on the road geometry, vehicle characteristics, and etc.
For origins including on-ramps in the traffic network, the queuing model is utilized.
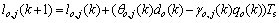 (6)
(6)
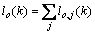 (7)
(7)
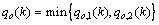 (8)
(8)
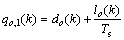 (9)
(9)
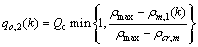 (10)
(10)
where lo refers to the queue length at origin o; lo,j represents the partial queue length at o that is destined to j; do refers to the traffic demand at o; θo,j is the composition rate, which represents the portion of do that is destined to j; qo refers to the actual network inflow via o, which is the minimum of the total origin demand, qo,1, and the allowed mainstream capacity, qo,2; γo,j represents the portion of qo that is destined to j; Qc represents the origin or on-ramp capacity when traffic flow is in the free flow condition, and ρmax refers to the maximum density.
For junction and bifurcation nodes in the network, the follow equations are used to describe the traffic flow.
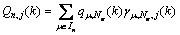 (11)
(11)
 (12)
(12)
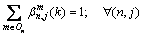 (13)
(13)
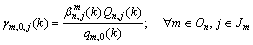 (14)
(14)
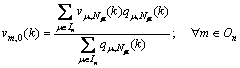 (15)
(15)
 (16)
(16)
where In refers to the set of links that enter node n; and On refers to the set of links that leave from node n; Qn,j represents the flow at node n that is destined to j, and it can be considered the flow for the BD pair (n, j); 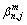 is called the splitting rate, which represents the portion of Qn,j that take link m.
is called the splitting rate, which represents the portion of Qn,j that take link m.
Equations (1)-(5) describe the traffic flow evolution on segment links (homogeneous motorway stretches). In the METANET model, a node is placed wherever there is a major change in the road geometry, and Eqs. (6)-(10) are used to describe the flow diversion or aggregation at the nodes. For the network origin links and on-ramps, traffic demand is received and then forwarded to the motorway network, and the queuing model (Eqs. (11)-(16)) is used. The link equations, node equations, and origin equations constitute the METANET model, which can be easily extended to any network configuration.
3 VMS-based routing control design
3.1 Routing control model
In the VMS-based route guidance system, the VMS board is often located in advance of the bifurcation (flow diversion point), and the traffic management authority delivers the route recommendations on the VMS board to influence the passing travelers’ route-choice behavior. In the routing control design, the route recommendation is directly considered as the control variable, and the routing control model is established firstly, which describes the influence of VMS route recommendation (control variable) on the distribution of traffic flow (system state).
For the multi-route choices network, the route set Rn,j is defined to consist of the alternative routes for the BD pair (n, j), and the routes are respectively numbered by 1, 2,…, cn,j, where cn,j is the number of the alternative routes for the (n, j) pair. Each route may consist of many links, and one link can be part of more than one route. The VMS board is located prior to the bifurcation node n and provides route recommendations towards the destination j. In the process of drivers making route-choice decisions, two assumptions are given. 1) The drivers who are destined to j will not change routes if the recommended route is the one that they are intended to take; 2) Drivers’ route-changing behavior is only caused by complying with the route recommendations, which indicates that the drivers will not change to the route that is not recommended by VMS. Therefore, the influence of VMS route recommendations on the flow distribution at route r (r∈Rn,j) can be classified into three cases: (a) no route recommendation; (b) route r is recommended; (c) another route (not r) is recommended, and then we can obtain:
 (17)
(17)
where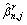 refers to the portion of Qn,j that takes route r under the routing control. Note that
refers to the portion of Qn,j that takes route r under the routing control. Note that holds, similarly as Eq. (13).
holds, similarly as Eq. (13). 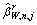 represents the portion of Qn,j that take route r in the absence of routing control, and it can be assumed to be known and time-invariant in the controller design. ξ refers to the compliance rate of drivers whose original route-choices do not match the recommended ones, and it describes drivers’ route-changing rate caused by following the route recommendations.
represents the portion of Qn,j that take route r in the absence of routing control, and it can be assumed to be known and time-invariant in the controller design. ξ refers to the compliance rate of drivers whose original route-choices do not match the recommended ones, and it describes drivers’ route-changing rate caused by following the route recommendations.
Equation (17) indicates the calculation of 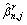 in three cases: (a) if VMS does not provide any route recommendation towards j,
in three cases: (a) if VMS does not provide any route recommendation towards j, 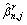 is equal to the corresponding value in the absence of routing,
is equal to the corresponding value in the absence of routing, 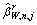 ; (b) if VMS recommends drivers to take route r towards j,
; (b) if VMS recommends drivers to take route r towards j, 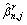 is equal to
is equal to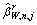 plus the percentage of drivers whose original route-choices are not route r but comply with the VMS indication (change to route r); (c) if VMS recommends a route other than r,
plus the percentage of drivers whose original route-choices are not route r but comply with the VMS indication (change to route r); (c) if VMS recommends a route other than r, 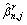 is equal to the portion of Qn,j that is intended to take route r and ignore VMS route recommendations (refuse to change route).
is equal to the portion of Qn,j that is intended to take route r and ignore VMS route recommendations (refuse to change route).
Then, the splitting rates at the bifurcation can be obtained as follows.
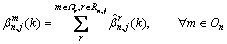 (18)
(18)
where Ωr refers to the set that comprises all the links of route r. Equation (18) indicates that the splitting rate 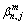 is the summation of
is the summation of 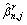 for routes that comprise the link m.
for routes that comprise the link m.
In order to describe the influence of VMS route recommendations on the flow distribution at each alternative route, 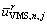 is introduced, which refers to the control component (projection) of VMS route recommendation on route r. Based on the above analysis, we can obtain
is introduced, which refers to the control component (projection) of VMS route recommendation on route r. Based on the above analysis, we can obtain
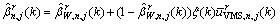 (19)
(19)
where the control component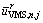 is defined in three cases, according to the route recommendations provided by VMS.
is defined in three cases, according to the route recommendations provided by VMS.
 (20)
(20)
For the traffic management authority, the controllable variable is when and what route recommendations are displayed on the VMS sign, and then the control variable in the route guidance system is defined.
 (21)
(21)
where uVMS,n,j refers to the control variable for the (n, j) pair in the VMS-based route guidance system.
According to Eqs. (20)-(21), the mapping relationship between the routing control signal uVMS,n,j and the corresponding control components can be established. If no route recommendation is provided, the routing control component on each alternative route is zero, while if one route is recommended, the control component on the recommended route is positive, and the control components on the un-recommended routes are negative. Then, the multi-dimensional vector , that consists of the control component at each alternative route for (n, j) pair, is defined.
, that consists of the control component at each alternative route for (n, j) pair, is defined.
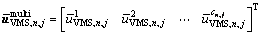 (22)
(22)
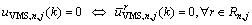 (23)
(23)
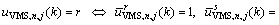
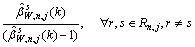 (24)
(24)
Above all, the routing control model for the multi-route diversion is proposed. In the route guidance control, the control (decision) variable is when and what route recommendation is displayed on the VMS board, represented by the uVMS,n,j(k) in Eq. (21). The traffic management authority dynamically regulates the control signal, and the influence of the control signal on each alternative route is obtained according to Eqs. (22)-(24), and finally the network flow distribution is affected (Eqs. (18)-(19)). It can be seen that the routing control model links the control variable with the traffic state, and it can describe the network configuration where there are any route choices for diversion.
3.2 Routing control design in MPC framework
MPC is an online rolling horizon optimization strategy in the closed-loop way, and it behaves robustness to the disturbances and model uncertainties. In MPC framework (Fig. 1), the current control action is applied by solving the optimization based on the measured current state and the predicted future state. Only the first value in the solved control sequence is applied to the system plant, and then the horizon shifts forward a time step, and the process is repeated, which is called the receding (moving) horizon optimization.
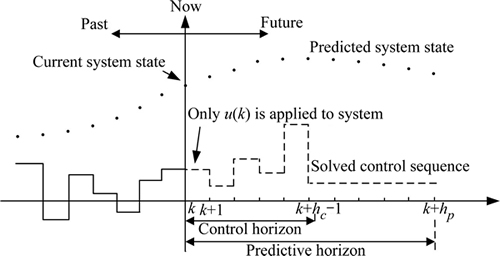
Fig.1 Scheme of MPC control strategy
In MPC control strategy, the system model is required for prediction. For route guidance system, the state space model is established based on the traffic flow model and the routing control model. The state vector is composed of the partial density for each segment ρm,i,j, speed for each segment vm,i, and the partial queue length for each origin and on-ramp lo,j. The route recommendations displaying on the VMS sign for each controlled BD pair uVMS,n,j are considered the control variables. The disturbance vector consists of the traffic demand for origins or on-ramps do, the composition rates θo,j, drivers’ route-changing rates ξ, and the variables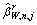 that describe drivers’ original route-choice behavior. According to the traffic flow model (Eqs. (1)-(16)) and the routing control model (Eqs. (18), (19), (21)-(24)), the nonlinear state space model for the VMS-based route guidance system can be obtained, and the dimensions of state vector, control vector, and disturbance vector depend on the utilized network configuration.
that describe drivers’ original route-choice behavior. According to the traffic flow model (Eqs. (1)-(16)) and the routing control model (Eqs. (18), (19), (21)-(24)), the nonlinear state space model for the VMS-based route guidance system can be obtained, and the dimensions of state vector, control vector, and disturbance vector depend on the utilized network configuration.
System optimum is considered the control objective, since the traffic management authority is in the dominant position in the route guidance system. In addition, the control cost of delivering route recommendations through the VMS, and the switching performances of routing control signals are considered in the objective function.
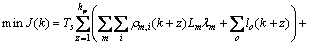
 (25)
(25)
where
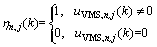 ;
;
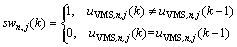 ;
;
J refers to the objective function; hp is the predictive horizon; and hc is the control horizon. The first item in Eq. (25) calculates the total time spent (TTS) for all the vehicles in network in the predictive horizon, and the vehicles waiting at the origins and on-ramps are included, and the second item refers to the routing control cost, and the last item is to punish the frequent switching of routing control signals. αu and αsw are the weighting parameters.
In the process of delivering route recommendations on the VMS, the switching interval of route recommendations should be larger than the minimum admissible switching interval, tadm, in order to avoid confusing drivers.
Generally, most followers of VMS route recommendations are often expected to take the shortest-time route (user-optimum), but actually, drivers can not exactly estimate the shortest time between two points, and a small extent of time delay caused by the route guidance is tolerated or even unnoticed. Therefore, the acceptable (tolerance) factor, φ (φ≥1) [20], is introduced, which describes the drivers’ maximum tolerance with the time delay by following the route recommendations, and the constraint regarding the control signal is established to guarantee that the route recommendations will only guide followers to the “acceptable” routes with the acceptable factor φ.
Constraint:
 (26)
(26)
where χr represents the travel time of route r, which can be estimated by Eq. (27); τn,j refers to the minimum travel time for the (n, j) pair. φ=1 indicates that only the fastest route is accepted by drivers, while φ>1 indicates that the routes are acceptable if the corresponding travel time is not greater than φ times that of the fastest route. The smaller the value of φ is, the more the followers are satisfied with the route guidance, while more demanding (strict) for the traffic management.
Travel time of a route can be calculated by summing the travel time of all the links that compose the route.
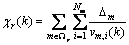 (27)
(27)
It can be seen that the routing control design in MPC framework will be finally transformed to an online non-linear integer programming (NIP), in which the integer routing control sequence [u(k), u(k+1),…, u(k+hc-1)]T are the variables to be solved.
In this section, a constrained system optimum routing strategy with the constraint regarding drivers’ acceptability with the route recommendations is designed, which can both meet the traffic management’s control objective, and improve drivers’ satisfaction with the VMS route guidance system.
4 Solving control strategy
In order to solve the NIP in each rolling optimization of MPC, the solving method is discussed in this section.
For the solved VMS routing control sequence in the control horizon, the switching vector is defined, which consists of the switching time instants of control signal, and the control increments implemented at the switching instants. Compared to the control sequence, the dimension of the switching vector is reduced, since only the information regarding the switching of the control signal is recorded. An example is used to describe the definition of the VMS switching vector. Assume that there is one VMS routing control variable in the controlled traffic network, the number of route-choices for the controlled BD pair is 3, the MPC control horizon is 15, the VMS control sequence, 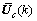 , is supposed to be [0 0 0 0 0 0 2 2 2 2 2 2 2 2 2]T, and the routing control value at the previous instant k-1 is 1. Then, the corresponding switching vector,
, is supposed to be [0 0 0 0 0 0 2 2 2 2 2 2 2 2 2]T, and the routing control value at the previous instant k-1 is 1. Then, the corresponding switching vector,  , can be obtained as follows.
, can be obtained as follows.

In the switching vector, the elements in the odd position are defined to record the time instants when the routing control signal switches, counting from the previous control instant, k-1, and the elements in the even position represent the control increments (△uVMS,n,j (k+z)=uVMS,n,j(k+z)-uVMS,n,j(k+z-1)) implemented at the switching time instants. In the above example, the routing control signal switches at the 1st (1→0), and 7th (0→2) position in 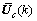 , so the first and the third elements in the switching vector are 1 and 7, which indicates that the switching of routing control signal happens at k instant and k+6 instant, respectively. The control increments implemented at the switching time instants are -1 (uVMS,n,j(k)-uVMS,n,j(k-1)=0-1=-1) and 2 (uVMS,n,j(k+6)-uVMS,n,j(k+5)=2-0=2), respectively, so the second and the fourth elements in the switching vector should be -1 and 2. For uniform expression, the negative values for the control increments are processed. Since the routing control variable can only take the values in the integer set {0,1,2, …cn,j}, the negative control increments can be transformed to the positive values by adding with cn,j+1. In other words, the control signal changes from 1 to 0 with cn,j=3, and the transformation of
, so the first and the third elements in the switching vector are 1 and 7, which indicates that the switching of routing control signal happens at k instant and k+6 instant, respectively. The control increments implemented at the switching time instants are -1 (uVMS,n,j(k)-uVMS,n,j(k-1)=0-1=-1) and 2 (uVMS,n,j(k+6)-uVMS,n,j(k+5)=2-0=2), respectively, so the second and the fourth elements in the switching vector should be -1 and 2. For uniform expression, the negative values for the control increments are processed. Since the routing control variable can only take the values in the integer set {0,1,2, …cn,j}, the negative control increments can be transformed to the positive values by adding with cn,j+1. In other words, the control signal changes from 1 to 0 with cn,j=3, and the transformation of 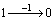 is equivalent to
is equivalent to 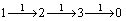 (cn,j+1 is considered to be a cycle period). Therefore, the control increment of -1 can be converted into the positive value 3, and the switching vector that corresponds to the
(cn,j+1 is considered to be a cycle period). Therefore, the control increment of -1 can be converted into the positive value 3, and the switching vector that corresponds to the 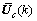 in the above example is [1 3 7 2]T.
in the above example is [1 3 7 2]T.
In the above way, the VMS routing control sequence in the control horizon can be transformed to the unique switching vector, and vice versa. Compared to the routing control sequence, the dimension of the switching vector decreases, and therefore, we will solve the switching vector, rather than directly solving the routing control sequence in the optimization, to simplify the on-line solving and improve the computation efficiency.
The length of the switching vector is twice the switching times of routing control signal in one control horizon, and the maximum admissible switching times Nmax can be obtained according to the constraint of the minimum admissible switching interval tadm. A dual-loop structure is designed to search the optimal switching vector. In the outer loop, the switching times, N, varies from 0 to Nmax (switching times is 0 indicates that the control signal remains unchanged in the control horizon). Once the switching times is fixed, which indicates that the length of switching vector is fixed, the inner loop is designed to search the corresponding optimal switching vector . The ultimate solution for the problem is obtained by comparing the objective values of all the
. The ultimate solution for the problem is obtained by comparing the objective values of all the (N=0, 1, 2,…, Nmax).
(N=0, 1, 2,…, Nmax).
Tabu search (TS), is a meta-heuristic searching method that extends local search procedure and allows non-improving solutions to be accepted, in order to escape from a local optimum [21]. TS is a powerful searching algorithm that has been applied with great success to many combinatorial problems. In the inner loop of the dual-loop optimization, TS algorithm is utilized to search the integer VMS switching vector. At each TS iteration, the neighboring solutions are generated from the current solution, and the neighborhood searching is performed. In our optimization problem, the solved variable is the VMS switching vector, and the neighborhood is defined, in which the action of plus or minus 1 for the elements in the switching vector is applied to the current solution. So, the neighboring solutions correspond to the modifications of VMS control sequence, which include the horizontal moves of the VMS switching instants (one-step left or right shift, see Fig. 2(a)), and the longitudinal moves of the control increments at the switching instant (one-step shift up or down, see Fig. 2(b)) in one control horizon, based on the current solution.
In order to speed up the searching process and take advantage of multi-core (or multi-CPU) architecture, the inner-loop searching can be carried out by parallel computing, and multiple TS algorithms are performed simultaneously, which is called parallel Tabu search [22]. The searching process (Fig. 3) is described as follows.
Step 1: Set the switching times of control signal N=0 (the routing control signal remains unchanged), and calculate the corresponding objective value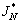 .
.
Step 2: Set N=N+1. If N≤Nmax, go to Step 3; else, go to Step 6.
Step 3: For fixed N, utilize the multi-core (or multi-CPU) architecture to implement the parallel TS searching from many initial points, and each individual core (or CPU) executes TS searching until the stopping criterion is satisfied (see Ref. [21] for the detail of TS algorithm).
Step 4: For fixed N, obtain the best switching vector  according to the best solution found in each core (or CPU), and then calculate the corresponding objective value
according to the best solution found in each core (or CPU), and then calculate the corresponding objective value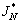 .
.
Step 5: Go to Step 2;
Step 6: Compare the object values of 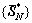 (N=0, 1, 2,…, Nmax), and find the ultimate best solution for the problem.
(N=0, 1, 2,…, Nmax), and find the ultimate best solution for the problem.
5 Simulation and discussion
The following hypothetical traffic network is considered for simulation, as shown in Fig. 4. In the tested network, there are three alternative routes from the bifurcation node n2 to the destination D1, which are L2—L3—L4—L5 (freeway, denoted as route 1), L7— L8— L9—L4—L5 (freeway, denoted as route 2) and L2— L12— L13—L14—L5 (arterial road, denoted as route 3).The VMS sign is located prior to the bifurcation node n2, providing route recommendations towards D1. All the links have two lanes. In the absence of routing control, it is assumed that 50% of the drivers at the bifurcation n2 will take route 1(geometrically shortest route) to D1, 40% take route 2, and the remaining 10% take route 3 (geometrically longest route).

Fig. 2 Illustration of neighborhood in TS:
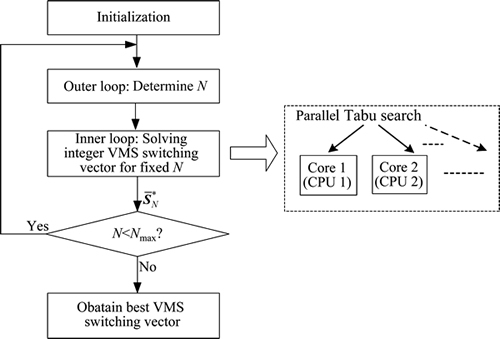
Fig. 3 Dual-loop searching for solving switching vector
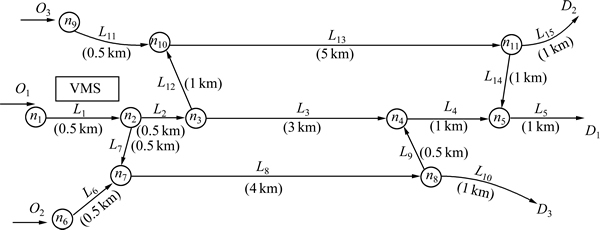
Fig. 4 Tested network
The values of the macroscopic traffic flow model parameters are chosen as: Ts=10 s, vf=110 km/h, ρcr,m=33.5 veh·(km·lane)-1, γ=60 km2/h, τ=18 s, κ=40 veh·(km·lane)-1, αm=1.636, ρmax=180 veh/km/lane. The segment length is chosen to be 1 km except for the links that are 0.5 km. The MPC routing control parameters are: hp=15 min, hc=10 min, the control interval Tc=5 min, φ=1.1, and the weighting parameters are αu=0.05 and αsw=0.5.
The simulation is conducted on the quad-core 3.5 GHz CPU, and the computation time for each optimization in MPC is less than 100 s, which is smaller than the control interval Tc, and therefore, the real-time implementation of routing control can be met sufficiently. With the increase of number of cores and CPUs, the on-line computation time at each MPC control step will be decreased dramatically.
In order to accord with reality, the stochastic fluctuations are introduced in the disturbances in the model simulation, and the traffic demand at origins (O1, O2 and O3) follow the Poisson distribution with the expectation value of 2800 veh/h, and a vehicle-to- vehicle crash happened at L3,3 at t=10 min, which blocks the link for 1 hour, the responses of the proposed routing control strategy are represented in Fig. 5.
In the absence of routing control, drivers don't know the traffic condition ahead, and vehicles gradually arrive to the place where crash happened. The traffic jam is formed at L3, which propagates backwards to bifurcation (Fig. 5(a)), and the queuing is formed at O1 (Fig. 5(e)). Route 1 is jammed (Fig. 5(b)), while route 2 and route 3 have much spare capacity, and the vehicles on route 2 and 3 are moving with larger speed (Figs. 5(c)-(d)), The network is underutilized, and the TTS value of all the network vehicles is 2698.6 veh·h.
When the routing control is implemented, the route recommendations are recommended to the drivers who will pass through the bifurcation node n2. Once the congestion on route 1 (the low flow speed and high traffic density) is detected, the routing controller diverts the flow that are intended to enter route 1 to route 2 and 3, as shown in Fig. 5(f). Due to the constraint regarding the drivers’ acceptability (Eq. (26)), only the routes that are acceptable with the tolerance factor φ will be recommended. Although the congestion on L3 could not be totally eliminated, the lasting time is decreased significantly (Fig. 5(b)), which can slower and alleviate the congestion spillback to the bifurcation (Fig. 5(a)), and the queuing at the network entrance O1 is totally avoided (Fig. 5(e)). The proposed routing control optimizes the traffic flow distribution and improves the network efficiency, and the TTS value is decreased to 1977.2 veh·h (26.73% improvement).
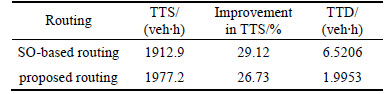
In addition, the proposed routing control strategy is compared with the traditional SO-based routing strategy. In order to reflect drivers’ satisfaction with the route guidance system, drivers’ total time delay (TTD) caused by following the route recommendations is calculated. The comparison results are listed in Table. 1.
According to Table 1, it can be seen that the SO-based routing focuses on the system optimum, and it performs better improvement in TTS, while it results in larger TTD, which may dissatisfy the followers and cause the large scale distrust and rejection of route recommendations after a long practical run. Compared to the SO-based routing, the proposed routing strategy performs a lit bit worse (less than 3%) in the TTS improvement, while in return, it reduces TTD significantly (69.40% reduction), which indicates that the drivers’ satisfaction with the route guidance system is improved. Above all, the proposed routing strategy can not only meet the traffic management authority’s control objective (increasing the network efficiency), but also improve drivers’ satisfaction with the route guidance system, which will increase drivers’ compliance to the route recommendations, and finally make the route guidance control more efficient.
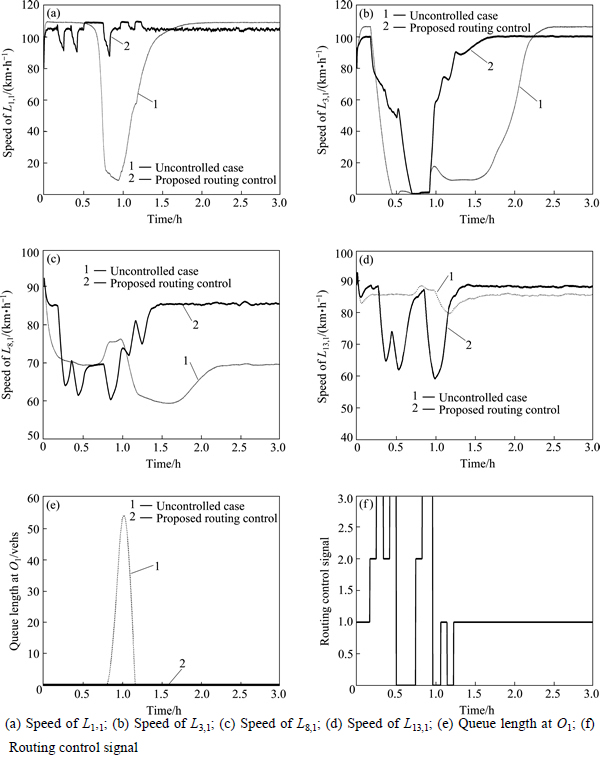
Fig. 5 Simulation responses:
Table 1 Comparison results of two routing controllers
6 Conclusions
For the network configuration with multi-route choices diversion, the VMS-based routing control model is established, in which the multi-dimension control vector is introduced to describe the influence of route recommendations on the flow distribution at each alternative route. Drivers’ compliance with route recommendations and their route-changing behavior are considered. Then the route recommendations displaying on the VMS are considered the control variables, and a real-time routing control strategy is designed in MPC framework. A system optimum routing with the constraint regarding drivers’ acceptability with the route recommendations is proposed. Simulation results show that the proposed routing control strategy can eliminate traffic congestion, optimize the flow distribution on each alternative route, and increase network efficiency in the multi-route choices network. In addition, compared to the SO-based routing, the proposed routing strategy meets the control requirements of the traffic management authority, and meanwhile decreases the followers’ time delay significantly, which will improves drivers’ trust and satisfaction with the route guidance system, increase drivers’ compliance to the route recommendations, and finally make the route guidance control more efficient.
References
[1] GOMES G, HOROWITZ R. Optimal freeway ramp metering using the asymmetric cell transmission model [J]. Transportation Research Part C-Emerging Technologies, 2006, 14(4): 244-262.
[2] BURGER M, van den BERG M, HEGYI A, de SCHUTTER B, HELLENDOORN J. Considerations for model-based traffic control [J]. Transportation Research Part C-Emerging Technologies, 2013, 35: 1-19.
[3] LI Zhi-bin, LIU Pan, WANG Wei, XU Cheng-cheng. Development of control strategy of variable speed limits for improving traffic operations at freeway bottlenecks [J]. Journal of Central South University, 2014, 21(6): 2526-2538.
[4] KACHROO P, OZBAY K. Solution to the user equilibrium dynamic traffic routing problem using feedback linearization [J]. Transportation Research Part B-Methodological, 1998, 32(5): 343-360.
[5] KOTSIALOS A, PAPAGEORGIOU M, MANGEASO M, HAJSALEM H. Coordinated and integrated control of motorway networks via non-linear optimal control [J]. Transportation Research Part C-Emerging Technologies, 2002, 10(1): 65-84.
[6] PAZ A, PETTA S. Behavior-consistent real-time traffic routing under information provision [J]. Transportation Research Part C-Emerging Technologies, 2009, 17(6): 642-661.
[7] SPILIOPOULOU A, KONORINAKI M, PAPAMICHAIL I, PAPAGEORGIOU M. Real-time route diversion control at congested motorway off-ramp areas - Part I: User-optimum route guidance [C]// IEEE Conference on Intelligent Transportation Systems. Hague, Netherlands: IEEE, 2013: 2119-2125.
[8] WANG Y B, PAPAGEORGIOU M, SARROS G, KNIBBE W J. Real-time route guidance for large-scale express ring-roads [C]// IEEE Intelligent Transportation Systems Conference. Toronto, Canada: IEEE, 2006: 17-20.
[9] XU T D, SUN L J, PENG Z R, HAN Y. Integrated route guidance and ramp metering consistent with drivers’ en-route diversion behavior [J]. IET Intelligent Transport Systems, 2011, 5(4): 267-276.
[10] HE Z B, GUAN
[11] SAWAYA O B, DOAN D L, ZILASKOPOULOS A K. Predictive time-based feedback control approach for managing freeway incidents [J]. Transportation Research Record, 2000, 1710: 79-84.
[12] MA Dong-fang, WANG Dian-hai, SONG Xian-min, JIN Sheng. Optimization method of signal timing parameters considering comprehensive efficiency of all approach lanes [J]. Journal of Central South University: Science and Technology, 2012, 43(4): 1557-1562. (in Chinese).
[13] MESSMER A, PAPAGEORGIOU M. Route diversion control in motorway networks via nonlinear optimization [J]. IEEE Transactions on Control Systems Technology, 1995, 3(1): 144-154.
[14] MAYNE D Q, RAWLINGS J B, RAO C V, SCOKAERT P Q M. Constrained model predictive control: Stability and optimality [J]. Automatica, 2000, 36(6): 789-814.
[15] SEBORG D E, MELLICHAMP D A, EDGAR T F, DOYLE III, FRANCIS J. Process dynamics and control, third edition [M]. USA: Wiley, 2010.
[16] LIGHTHILL M J, WHITHAM G B. On kinematic waves II: A theory of traffic flow on long, crowded roads [C]// Proceedings of The Royal Society of London, London, UK: RSL, 1955: 317-345.
[17] DAGANZO C F. The cell transmission model—a dynamic representation of highway traffic consistent with the hydrodynamic theory [J]. Transportation Research Part B-Methodological, 1994, 28(4): 269-287.
[18] TANG Tie-qiao, LI Chuan-yao, HUANG Hai-jun, SHANG Hua-yan. Macro modeling and analysis of traffic flow with road width [J]. Journal of Central South University, 2011, 18(5): 1757-1764.
[19] MESSMER A, PAPAGEORGIOU M. METANET: A macroscopic simulation program for motorway networks [J]. Traffic Engineering and Control, 1990, 31(9): 466-470.
[20] JAHN O, MOHRING H R, SUHULZ A S, STIER-MOSES N E. System-optimal routing of traffic flows with user constraints in networks with congestion [J]. Operations Research, 2005, 53(4): 600-616.
[21] TAILLARD E, BADEAU P, GENDREAU M. A Tabu search heuristic for the vehicle routing problem with soft time windows [J]. Transportation Science, 1997, 31(2): 170-186.
[22] WARDONO B, FATHI Y. A tabu search algorithm for the multi-stage parallel machine problem with limited buffer capacities [J]. European Journal of Operation Research, 2004, 155(2): 380-401.
(Edited by DENG Lü-xiang)
Foundation item: Projects (61304203, 51409157) supported by the National Natural Science Foundation of China; Project (12ZR1444800) supported by the Natural Science Foundation of Shanghai, China
Received date: 2015-09-20; Accepted date: 2016-03-01
Corresponding author: LUO Li-hua, PhD; Tel: +86-21-38282355; E-mail: lhluo@shmtu.edu.cn

