DOI: 10.11817/j.issn.1672-7207.2016.07.011

薄壁小直径管道导波探伤的传感器布置方案优化

王伟¹，游鹏辉²，钟万里¹，谢涛²，徐俊²，钟力强¹，肖晓晖²

(1. 广东电网公司电力科学研究院，广东 广州，510080；

2. 武汉大学 动力与机械学院，湖北 武汉，430072)

摘要：研究传感器布置对导波沿薄壁金属管道的频散特性、模态转换和缺陷定位的影响规律。其步骤为：首先，采用ANSYS软件建立薄壁小直径的无缺陷管道和缺陷管道有限元模型；采用瞬态动力学分析方法，对管道端部周向各节点施加轴向瞬时位移载荷，模拟超声传感器激发L(0,2)模态波；根据脉冲-回波信号的时间历程曲线，定义回波分辨率、反射系数。其次，分析缺陷的轴向位置精度以及4种传感器布置方案对导波频散、模态转换、周向定位和反射系数的影响。研究结果表明：增加传感器数量可有效抑制弯曲模态和导波频散的发生，并增强回波信号的幅值；当传感器数量小于4个时，难以对裂纹缺陷进行周向定位；反射系数随传感器数量的增加呈线性增大。

关键词：管道；导波；传感器布置；频散特性；反射系数

中图分类号：TM8；TM113         文献标志码：A         文章编号：1672-7207(2016)07-2254-06

Optimization of guided wave sensors distribution along thin-walled small-diameter pipe

WANG Wei¹, YOU Penghui², ZHONG Wanli¹, XIE Tao², XU Jun², ZHONG Liqiang¹, XIAO Xiaohui²

(1. Electric Power Research Institute of Guangdong Power Grid Company, Guangzhou 510080, China;

2. College of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China)

Abstract: The influence of sensor distribution scheme on the frequency dispersion characteristics, modal conversion and defect localization of guided wave along thin-walled metal pipe was investigated. The procedures were as follows. Firstly, the models of defective and non-defective finite element pipes were built using ANSYS software. Axial displacement was exerted to circumferential nodes in the end of pipe based on the transient dynamic analysis methods, and ultrasonic sensor activating L(0,2) mode was simulated. Then, according to time-history curves of the pulse-echo, characteristic parameters such as echo resolution and reflection coefficient were defined. Secondly, the axial defect location precision, as well as the influence of four sensor distribution schemes on the guided wave dispersion, modal conversion, circumferential localization and reflection coefficient were analyzed. The results show that bending modal and wave dispersion can be inhibited effectively while amplitude of echo signal can be amplified by adding sensors. It is difficult to locate crack defects circumferentially when the number of sensors is less than 4.And the reflection coefficient increases linearly with the increase of the number of sensors.

Key words: pipe; guided wave; sensor distribution; dispersion characteristics; reflection coefficient

薄壁金属管道在服役过程中由于腐蚀或老化等因素造成的缺陷常常导致管道发生泄漏事故，不仅造成经济损失，而且对生态环境造成威胁，因此，缺陷检测对管道安全至关重要。针对金属管道缺陷，无损检测是一种有效的技术途径，其中超声导波因具有传输距离远、检测效率高等优点具有广阔的应用前景。近年来，超声导波检测技术发展迅速，频散特性和信号传播幅值是管道缺陷检测的重要影响因素，而导波传感器数量的选择与布置方案是研究的关键。在导波理论方面，FLETCHER等^[1]利用共同源(CSM)的方法合成集中导波，使反射系数增大1倍，提高了缺陷检测的灵敏度；DEMMA等^[2]发现虽然低频扭转导波对周向缺陷不敏感，但可以用来检测有较大轴向尺寸的缺陷；YUEMIN等^[3]推导了导波在管道中传播方向的理论公式，并进行了数字模拟和实验研究，得到传感器布置间隙计算公式。在模拟和实验研究方面，ALLEYNE等^[4]利用脉冲回波法激励超声波脉冲，并对由缺陷引起的回波信号进行分析，通过回波幅判断缺陷的程度；WANG等^[5]使用L(0,2)模态波研究了缺陷两侧和不同尺寸参数缺陷的反射信号，更加准确地提取管道缺陷尺寸，研究缺陷对导波的反射规律； GALVAGNI等^[6]等用T(0,1)模态通过模拟和实验研究了考虑管道支撑下的管道导波传播，绘制了频散曲线，得出区分缺陷和简单支撑的方法；YANG等^[7]模拟不同频率模态波检测直管和弯管缺陷，得出管道缺陷定位误差随频率的增大而增大；ALLEYNE等^[8]研究指出模态T(0,1)比模态L(0,2)更易激发，但对于充液管道来说，模态L(0,2)的信噪比会降低，极易产生模态转变而导致误判；PETER等^[9]提出利用MP 处理数据，不仅提高信噪比，而且可以直接、准确地判断裂纹轴向位置。国内近年利用超声导波进行管道检测的理论和实验研究。程载斌等^[10]对超声导波在管道裂纹缺陷检测进行了数值模拟，得到了管道的周向裂纹长度和宽度对回波信号影响的关系；董为荣等^[11]运用有限元分析法，对目前现场检测中应用的L(0,2)及T(0,1)模态导波在管中传播过程进行数值模拟研究，给出了缺陷回波反射系数与缺陷横截面积各影响因素之间的关系曲线，近似判定缺陷的几何尺寸；孙广开等^[12]应用ANSYS有限元分析程序模拟超声导波的传播及遇到缺陷的反射回波情况，较准确地定位了缺陷位置；孔双庆^[13]模拟了不同模态、频率和周期的导波在有缺陷管道中的回波特征，判定管道缺陷损伤程度及其轴向定位；他得安等^[14]在自由管材下通过实验研究了导波幅值和波包宽度随传播距离的变化情况；何存富等^[15]采用轴对称激励接收的方法，通过多组实验对导波检测中传感器数量和频率特性进行了研究，并得出反射回波幅值与传感器的固有特性有关；马书义等^[16]计算了不同几何尺寸管道中 L(0,2)和 L(0,1)导波非频散段的限制频率，得出限定或最小化缺陷回波分辨距离可获得最佳的导波激励信号周期及检测频率或频段的结论；王悦民等^[17]研究了管道中L(0,2)导波起始截止频率与管道直径和壁厚的变化关系，研究结论为在整个频率范围内进一步选择合适的检测频率提供了参考。从上述研究结果可知导波的频散特性和信号传播幅值是影响管道检测的重要因素，然而目前研究主要集中于管道尺寸对其影响方面，而对传感器数量对导波的频散特性及信号传播幅值的影响研究较少，为此，本文作者对传感器数量进行研究，以便为管道实际检测提供指导。为了产生沿管道传播的轴对称导波，需要将足够数量的传感器等间距地沿管道圆周方向布置；考虑到电厂实际管道直径，传感器数量受到限制，本文在不同传感器数量的情况下，利用L(0,2)模态导波对管道裂纹检测进行数值模拟，研究传感器布置对导波频散特性、模态转换及反射系数的影响，建立导波反射系数和传感器数量之间的关系曲线。

1  薄壁管中的导波

1.1  导波的模式及频散现象

管中导波有3种模式：纵向导波模式(L模式)、弯曲模式(F模式)和扭转模式(T模式)。这3种模式的导波分别用L(n,m)，F(n,m)和T(n,m)表示，其中n和m分别代表周向和径向模态参数且均为整数。L模式和T模式为轴对称模式，F模式为非轴对称模式。

由弹性动力学理论首先得到无限长空心圆柱体中导波传播的频散方程，通过对频散方程求解可得到空心圆管中导波传播的频散曲线。由于导波的频散和多模态特性，使得导波对金属管道的缺陷定位非常困难，因此，必须根据频散曲线的特点，选择特定的导波模态进行数值模拟。

本文仿真采用的是L(0,2)模态。该模态有2个显著的优点：首先，纵波L(0,2)在40~200 kHz范围内几乎没有频散现象，即导波信号波包在传播过程中不会发生明显的变形而导致无法识别；其次，该模态传播的速度最快，因此，最先到达的就是目标信号，能够提高特征识别的精度。

1.2  导波基本检测理论

导波沿管道传播的波速只与材料的性能有关，其纵波波速为^[18]

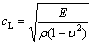
式中：c_L为L(0,2)模态导波在管中的传播速度，m/s；E为材料弹性模量，Pa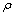；为材料密度，kg/m³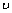；为泊松比。

根据导波信号时域图，可得出初次波与缺陷回波信号到达的时间间隔Dt。设缺陷离管端距离为x，则有以下关系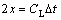：。经多次测量，可以精确确定缺陷离管道激励端的距离，并且该方法可用作导波波速拟合，比较拟合出的波速是否与理论波速相吻合。

2  薄壁管道中超声导波的数值模拟

2.1  有限元模型的建立

管道模型包括无缺陷管道和缺陷管道；管道模型几何参数包括长度l、内径r和管壁厚h；材料参数包括弹性模量E、材料密度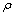和泊松比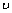。建立缺陷管道模型时，直接建立带有裂纹的三维管道模型。为了减少在划分时网格单元的畸变，划分网格前对管道模型进行适当切割，以提高模型网格质量。缺陷尺寸参数包括距激发端面轴向距离l₁、周向角度q、径向深度R和轴向长度W，如图1所示。

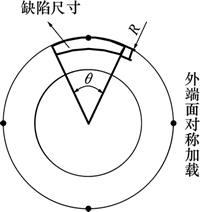
图1  管道缺陷尺寸参数

Fig. 1  Parameters of pipe defect

有限元模型采用solid45单元类型。根据单元和时间参数计算公式得模型单元长度L_E、总计算时间T、时间步长D。为提高计算精度，缺陷处网格更小。设网格单元长度为L_E0，缺陷管道模型如图2所示。

实际检测时，管道有包覆层而且被埋于水下、土壤或其他物质中，边界状况复杂，不利于传感器的安装。本文定量地研究传感器数量和导波反射系数之间的关系，因此，对管道模型的边界条件进行简化。加载时，管道模型的内外都设为真空，对管道的非激发端面施加固定约束。

针对所建模型，采用ANSYS瞬态动力学模块中完全瞬态分析法进行超声导波检测数值模拟。

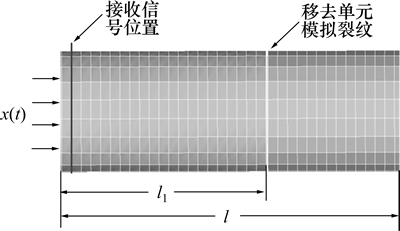
图2  管道模型示意图

Fig. 2  Schematic diagram of pipe model

2.2  导波激励与接收

在管道左端部激励纵向模态导波L(0,2)，即在端部的节点上加载对应的位移曲线，选择激励频率为140 kHz，激励信号采用调制的10周期正弦信号。这种激励信号的频域能量集中，能有效地降低能量的发散，抑制导波的频散。激励信号的表达式为^[13]

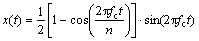
式中：n为选用的单音频数目；f_c为信号中心频率，Hz；t为时间，s。

通过对管道左端的端部周向各节点预加轴向瞬时位移载荷模拟纵向入射导波，监测节点位移接收反射波，接收信号位置距导波信号激发端1个单元长度，如图1与图2所示。

2.3  回波信号特征提取

裂纹管道的回波信号时程曲线如图3所示。接收节点检测到3组信号：激励信号x(t)，从裂纹反射回来的回波信号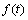，从管道末端反射回来的回波信号d(t)。

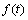的波形时长相对x(t)的波形时长有所增加，即出现导波传播过程的频散效应。为了描述导波信号在传播过程中的频散程度和提取反射回波信号，定义以下2个参数。

1) 回波分辨率S，为端部回波信号d(t)在时域上的持续时间T₁与激励信号x(t)在时域上的持续时间T₀之比，即S=T₁/T₀。S越大，频散越严重。

2) 反射系数C，为反射回波的幅值A₁与入射波的幅值A₀之比，即C=A₁/A₀。

导波在管道缺陷和端面处会发生反射，在缺陷处的反射系数大于同周向其他位置的反射系数。

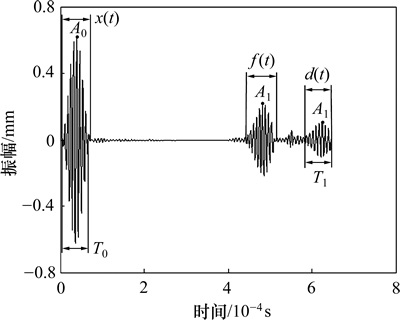
图3  缺陷回波时间历程

Fig. 3  Time history of defect echo

3  结果与分析

3.1  仿真工况

管道的几何尺寸主要是根据实际检测管道和仿真计算量而定。本文研究模拟的管道几何参数为：l=1 500 mm，r=76 mm，h=5.5 mm；缺陷尺寸参数为：l₁=1 m，q=50°，R=5.5 mm，W=1 mm。管道的材料选择为T24钢，其材料参数为：r=7.890 t/m³，E=2.0×10¹¹ Pa，u=0.3。

建立管道几何模型及确定所采用的单元之后对管道模型进行网格划分。管道的圆周划分数由实验管道环向布置的传感器个数决定^[15]，周向划分数为加载传感器数量的1~3倍。根据仿真计算精度和计算机配置，模型圆周方向的网格数为32个，厚度方向的网格数为2个，总网格数为19 200个。设置的计算参数为：T= 0.68 ms，L_E0=5 mm，D=0.8 μs。

建立无缺陷管道和缺陷管道，分别对对称加载4种传感器数量的2种模型进行数值模拟。

3.2  波速拟合及轴向定位

裂纹的轴向定位是根据式(2)计算得到，通过激 励波和管道端面反射波的到达时刻计算得到Dt=5.788 2×10^-4 s，导波的模拟速度为5 171.2 m/s。由式(1)知导波速度理论值为5 277.8 m/s，拟合结果较好。

根据激励波和管道裂纹反射波的到达时刻测得Dt=4.06×10^-4 s，裂纹轴向距离为1.05 m。裂纹实际轴向距离为1 m，缺陷定位误差为5%，在检测误差范围内。

3.3  导波频散

频散现象在时域中的表现为：某一模态波的包络线随传播距离的增加不断拉长，严重降低了检测信号的信噪比，若对应模态导波频散现象严重，则激发信号的包络线也容易变宽。为避免不规则管道缺陷对导波频散的影响，采用无缺陷管道进行仿真，对接收信号位置处周向32个节点的位移时程曲线进行简单叠加，以消除弯曲波的影响。

布置不同传感器数量的无缺陷管道端面反射系数见图4。由图4可知：当传感器数量由32个减小到4个时，回波分辨率S由1.12增大到1.49，L(0,2)模态端面反射回波包络线变宽，同时信号峰值幅度衰减变快，大大影响导波的检测距离，这会对实际应用造成不利影响，如分辨率、幅度和检测距离减小，所以，应布置足够的传感器以抑制导波频散。

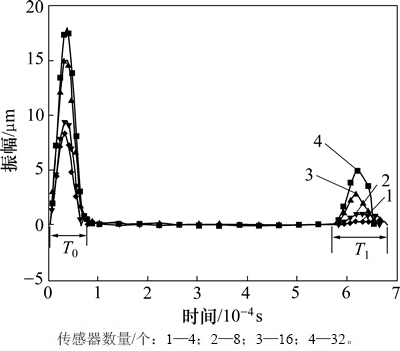
图4  不同传感器数量的无缺陷管道端面回波时程曲线

Fig. 4  Echo time history curve of non-defective pipes end with different sensor numbers

3.4  管道缺陷模态转换

模拟对称加载的4种传感器数量对缺陷反射系数的影响见图5。分析图5可知：当传感器的数量增多时，激励信号的幅值增大；缺陷反射回波大致相同，都出现了L(0,2)模态，且波形极清晰；当传感器数量为8个和4个时缺陷反射回波中还出现了其余模态的包络线。通过缺陷与发射端面实际距离计算出该模态导波的模拟速度为3 857.9 m/s，对比频散曲线可知该模态为弯曲模态F(3,3)，数值模拟结果与实验结果较吻合。分析频散曲线可知：140 kHz处可激励的最高模态为F(13,1)，传感器数量大于在该频率处激励的最高模态对应的数值13，由于各弯曲模态间的相互干涉，会抑制弯曲模态波，从而增强轴对称模态波。因此，足够的传感器数量不仅可以增强激励信号的幅值，而且可以有效地抑制弯曲模态。

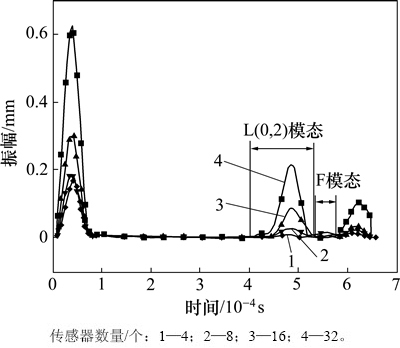
图5  不同传感器数量的缺陷回波时程曲线

Fig. 5  Echo time history curves of defect with different sensor numbers

3.5  裂纹缺陷的周向定位

缺陷的周向定位是根据管道有限元模型上各信号接收节点的周向位置，将各节点的周向弧度作为横坐标，节点对应的反射系数为纵坐标，绘制周向反射系数的极坐标图。通过分析周向反射系数图的曲线轨迹对缺陷进行周向定位。

传感器数量变化时裂纹缺陷的周向定位如图6所示。其中，图6(b)所示是传感器数量为4个和8个时的放大图。分析图6(b)可知：不同传感器数量的缺陷反射回波的幅值变化趋势大致相同，缺陷一侧的反射系数增大速度明显高于非缺陷一侧反射系数的增大速度，因此，缺陷的导波反射系数在圆周方向的分布特征也越来越明显，但当传感器数量为4时，已不能明显地区分缺陷的周向位置，且反射系数幅值降低，不易识别。这说明传感器数量的变化不会改变反射回波的幅值变化趋势，但随着传感器数量增加，可以有效加强信号传播幅值。

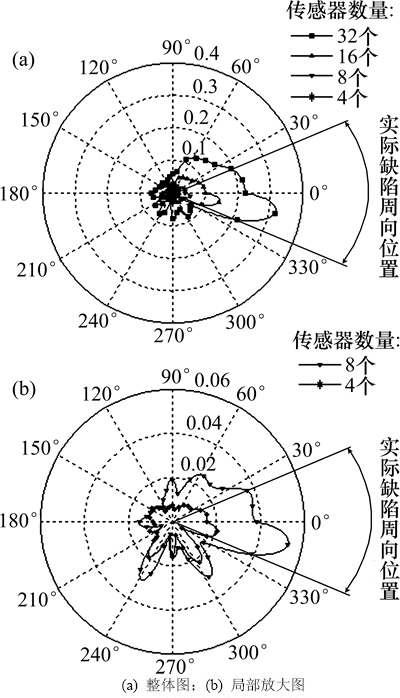
图6 不同传感器数量的反射系数

Fig. 6  Reflection coefficients for different sensor numbers

3.6  传感器数量与反射系数之间的关系

缺陷管道回波反射系数见表1。

表1  实验管道的反射系数

Table 1  Reflection coefficients of pipe

根据表1绘制缺陷管道反射系数C和传感器数量N的关系曲线，如图7所示。分析图7可知：缺陷管道的反射系数与感器数量呈现出良好的线性关系，这一点与实验数据所表现出的线性关系相吻合。缺陷管道反射系数 C与传感器数量N的线性拟合关系式为：C=0.010 8N-0.027 7。

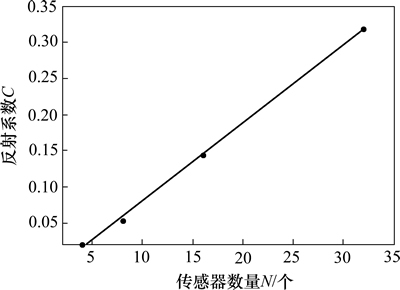
图7  传感器数量与反射系数的关系

Fig. 7  Relationship between sensor number and reflection coefficient

4  结论

1) 通过无缺陷管道的脉冲-回波信号时域振动曲线，计算L(0,2)模态波的模拟波速，利用模拟波速进行缺陷的轴向定位，得到其定位精度，验证了本文模型的正确性，包括模型的约束、导波的激发、计算参数等。

2) 增加传感器数量能够抑制弯曲模态和导波频散，提高特征识别的精度。

3) 随着传感器数量的改变，各仿真工况中的缺陷回波幅值变化趋势大致相同。当传感器数量小于4个时，缺陷回波反射幅值降低，难以对裂纹缺陷进行周向定位。

4) 缺陷管道反射系数C与传感器数量N呈线性变化关系，其拟合关系式为：C=0.010 8N-0.027 7。

参考文献：

[1] FLETCHER S, LOWE M J S, RATASSEPP M, et al. Detection of axial cracks in pipes using foused guided waves[J].Journal of Nondestructive Evaluation, 2012, 31(1): 56-64.

[2] DEMMA A, CAWLEY P, LOWE M, et al. The reflection of the fundamental torsional mode from cracks and notches in pipes[J]. Dynamic Method for Damage Detection in Structures, 2008, 499(2): 195-209.

[3] YUEMIN W, LIHUA S, CHUANJUN S, et al. Theoretical and experimental research on controlling guided waves propagation direction in pipes[C]// Electronic Measurement & Instruments (ICEMI), 2011 10th International Conference. Chengdu, China, IEEE, 2011: 28-32.

[4] ALLEYNE D N, PAVLAKOVIC B, LOWE M J S, et al. Rapid, long range inspection of chemical plant pipework using guided waves[J]. Key Engineering Materials, 2001, 43(2): 180-187.

[5] WANG X, PETER W T, MECHEFSKE C K, et al. Experimental investigation of reflection in guided wave-based inspection for the characterization of pipeline defects[J]. Nondestructive Testing and Evaluation International, 2010, 43(4): 365-374.

[6] GALVAGNI A, CAWLEY P. The reflection of guided waves from simple supports in pipes[J]. The Journal of the Acoustical Society of America, 2011, 129(4): 1869-1880.

[7] YANG H, WANG C. Study on simulation of non-destructive testing for pipeline defects by ultrasonic guided waves[C]// Cross Strait Quad-Regional Radio Science and Wireless Technology Conference (CSQRWC). Harbin, China: IEEE, 2011: 238-242.

[8] ALLEYNE D N, VOGT T, CAWLEY P. The choice of torsional or longitudinal excitation in guided wave pipe inspection[J]. Insight-Non-Destructive Testing and Condition Monitoring, 2009, 51(7): 373-377.

[9] PETER W T, WANG X. Characterization of pipeline defect in guided-waves based inspection through matching pursuit with the optimized dictionary[J]. NDT & E International, 2013, 54: 171-182.

[10] 程载斌, 王志华, 张立军, 等. 管道超声纵向导波裂纹检测数值模拟[J]. 应用力学学报, 2005, 21(4): 76-79.

CHENG Zaibin, WANG Zhihua, ZHANG Lijun, et al. Numerical simulation of crack detection in pipes using ultrasonic longitudinal guided-wave[J]. Chinese Journal of Applied Mechanics, 2005, 21(4): 76-79.

[11] 董为荣, 帅健, 许葵. 管道腐蚀缺陷超声导波检测数值模拟研究[J]. 机械强度, 2009, 30(6): 988-993.

DONG Weirong, SHUAI Jian, XU Kui. Numerical simulation of corrosion detection in pipes using ultrasonic guided waves[J]. Journal of Mechanical Strength, 2009, 30(6): 988-993.

[12] 孙广开, 焦阳, 李光海, 等. 超声导波管道缺陷检测数值模拟[J]. 河北工业科技, 2010, 27(1): 18-21.

SUN Guangkai, JIAO Yang, LI Guanghai, et al. Numerical simulation of defect detection in pipes using ultrasonic guided waves[J]. Hebei Journal of Industrial Science and Technology, 2010, 27(1): 18-21.

[13] 孔双庆. 管道超声导波检测的数值模拟和实验研究[D]. 大连: 大连理工大学工程力学系, 2011: 24-41.

KONG Shuangqing. Numerieal simulation and experimental investigation of defect detection in pipes using ultrasonic guided waves[D]. Dalian: Dalian University of Technology. Department of Engineering Mechanics, 2011: 24-41.

[14] 他得安, 易勇, 刘镇清. 传播距离对管中导波传播特性的影响[J]. 无损检测, 2004, 25(11): 553-556.

TA Dean, YI Yong, LIU Zhenqing. Influence of propagation distance on the characteristics of ultrasonic guided wave propagation in pipes[J]. NDT, 2004, 25(11): 553-556.

[15] 何存富, 刘增华, 郑璟瑜, 等. 管道导波检测中传感器数量和频率特性研究[J]. 北京工业大学学报, 2005, 30(4): 393-397.

HE Cunfu, LIU Zenghua, ZHENG Jingyu, et al. Study on the number and the frequency characteristic of transducers in pipe inspection using guided waves[J]. Journal of Beijing University of Technology, 2005, 30(4): 393-397.

[16] 马书义, 武湛君, 刘科海, 等. 空心圆管中导波频散特性与检测频率选择[J]. 机械工程学报, 2014, 50(20): 8-17.

MA Shuyi, WU Zhanjun, LIU Kehai, et al.Dispersion characteristics and inspection frequency selection of guided waves in hollow cylinders[J]. Journal of Mechanical Engineering, 2014, 50(20): 8-17.

[17] 王悦民, 沈立华, 申传俊, 等. 管道导波无损检测频率选择与管材特征关系[J]. 机械工程学报, 2009, 45(8): 243-248.

WANG Yuemin, SHEN Lihua, SHEN Chuanjun, et al. Relationship between frequency selection and pipe characteristics for guided waves NDT[J]. Journal of Mechanical Engineering, 2009, 45(8): 243-248.

[18] 董为荣, 帅健, 许葵. 管道T(0,1)模态导波检测数值模拟研究[J]. 无损检测, 2008, 30(3): 149-152.

DONG Weirong, SHUAI Jian, XU Kui. Numerical simulation study of detection in pipes using T(0,1) mode ultrasonic guided waves[J]. NDT, 2008, 30(3): 149-152.

(编辑  陈灿华)

收稿日期：2015-09-31；修回日期：2015-11-22

基金项目(Foundation item)：国家自然科学基金资助项目(51175383) (Project(51175383) supported by the National Natural Science Foundation of China)

通信作者：肖晓晖，博士，教授，从事特种机器人与微操作机器人研究；E-mail: xhxiao@whu.edu.cn