3DEC modeling on effect of joints and interlayer on wave propagation

WANG Wei-hua(王卫华), LI Xi-bing(李夕兵), ZUO Yu-jun(左宇军),

ZHOU Zi-long(周子龙), ZHANG Yi-ping(张义平)

School of Resources and Safety Engineering, Central South University, Changsha 410083, China

Received 5 July 2005; accepted 30 September 2005

Abstract: Firstly, studies on propagation of one-dimensional normally incident wave in rock mass containing no joint, a single joint and two parallel joints were conducted by Three Dimensional Distinct Element Codes(3DEC). By comparison of the modeling results with the theoretical solutions, it has been found that a good agreement between them has been achieved. It is verified that the 3DEC is capable of modeling wave propagation in rock masses. Secondly, propagation of normally incident P-wave across two parallel joints was studied. The modeling results show that transmission coefficient increases with the increasing ratio of joint spacing to wavelength at first, then decreases with the increasing ratio of joint spacing to wavelength, lastly keeps constant. Finally, effect of interlayer on wave propagation is investigated. It is shown that interlayer results in marked attenuation and leading phase, and that attenuation increases with the increasing frequency and the increasing thickness of interlayer.

Key words: three dimensional distinct element codes (3DEC) modeling; wave propagation; joint; interlayer

1 Introduction

Natural rock mass is not homogeneous, and it is full of various weak planes with different structures and different geological mechanisms, such as fractures, joints, and cracks. These structural weak planes seriously hinder and affect the propagation of stress waves in rock mass. Therefore, many efforts have been made to study the effect of rock joints on wave propagation theoretically and experimentally[1-10].

Studies on responses of rock mass and rock structures under dynamic loading have been conducted primarily through numerical modeling, as laboratory and in-situ dynamic testing on rock mass and rock structure usually involves extremely high cost. In the continuum-based numerical calculation method, discontinuity of rock mass is depicted by the special element, such as joint element in Finite Element Method [11], interface element in Finite Element coupling Boundary Element[12] and slip interface in Finite Difference Method[13]. However, these methods are only valid for the conditions that joint number and displacement are very small, not valid for the situation that joints quantities are very large. When cracks sizes are small and quantities are great, discontinuity of rock mass is very difficult to be characterized by continuum-based model. Distinct Element Method[14], originated by CUNDALL in 1971 is used to simulate the response of the discontinuity medium. The jointed rock masses are treated as composition of rock blocks and discontinuity between rock blocks; large displacements along discontinuities and rotations of blocks are allowed in the Distinct Element Method, so, the characterization of nonlinear and large deformation in jointed rock mass may be simulated more really than by other methods.

Universal Distinct Element Codes (UDEC) and Three Dimensional Element Codes (3DEC) are commercial software developed by CUNDALL and his co-workers, which has been used to study the responses of jointed rock mass under static or dynamic loading. The UDEC modeling on the effects of the friction of a single rock fracture with a limited shear strength on the propagation of a normally incident one-dimensional shear wave has been conducted by LEMOS[15]. The magnitudes of reflection and transmission coefficients representing the effects of the fracture on wave attenuation are numerically determined. The numerical results agree well with the analytical solutions obtained by MILLER. BRADY et al[16] conducted studies of two-dimensional UDEC modeling on the slip of a fracture due to an explosive line source. UDEC results showed an agreement with the analytical solutions obtained by DAY. CAI and ZHAO[17], CHEN and ZHAO[18, 19], and ZHAO[20] used UDEC to model the blast wave propagation in fractured rock masses. It has been shown that the rock masses containing multiple fractures have greater and faster attenuation of the blast wave than the continuous media. KULATILAKE et al[21] studied the effect of intermitted joints on the deformation of jointed rock mass through 3DEC. LI et al[22] and GUO et al[23] used three dimensional discrete element to simulate the excavation of permanent ship-lock in Three Gorges and propagation of explosive waves. In conclusion, studies on the dynamic responses of jointed rock mass by 3DEC are underway. The propagation of stress wave in jointed rock mass is simulated by 3DEC in the present study. Firstly, propagation of one-dimensional wave in rock mass containing no joint, a single joint and two parallel joints is simulated; secondly,  wave propagation in rock mass containing interlay is simulated; Finally calculating results are discussed.

2 Modeling procedure

2.1 Propagation of one-dimensional wave in intact rock

The mesh size of the calculating model has significant influence on the accuracy of numerical results wherever the model is based on continuum or dis continuum model. Theoretically, the model with a finer mesh size can produce more accurate results. The mesh size larger than a certain limitation may result in the numerical distortion of wave presentation. Based on the study on the mesh size limitation in the Finite Element Method, KUHLEMEYER and LYSMER[24] proposed that the largest mesh size must be smaller than 1/8-1/12 of the smallest wavelength for the accurate results. Deformable blocks are subdivided into a mesh of finite difference elements in 3DEC, which satisfies the requirement of accuracy. First, modeling of one- dimensional wave propagation in an intact rock rod with finite length is carried out to determine the selection of mesh size in 3DEC modeling. In addition, the numerical results are regarded as a reference for comparison with the case of wave propagation in jointed rock mass.

The geometry of the model is shown in Fig.1(a), where the length in the y-direction is 300 m, and the thickness in x-direction is 10 m, and the height in the z-direction is 10 m. The dynamic mechanical properties of rock material are shown in Table 1. A sine wave plus with the amplitude, 1 MPa is applied to the left boundary (y=-150 m) and propagates from the left to the right along the y-direction. The incident wave frequency is 20 Hz. The left and right boundaries are set as no-reflection boundaries, while the upper and lower boundaries are defined as fixed boundaries in the z-direction, and the front and back boundaries are defined as fixed boundaries in the x-direction. Two measurement points are located at y=-140 m and y=140 m to record the stress history. On the other hand, supposing that there is no damping in rock medium, so, an elastic wave propagates through the rock bar without attenuation.

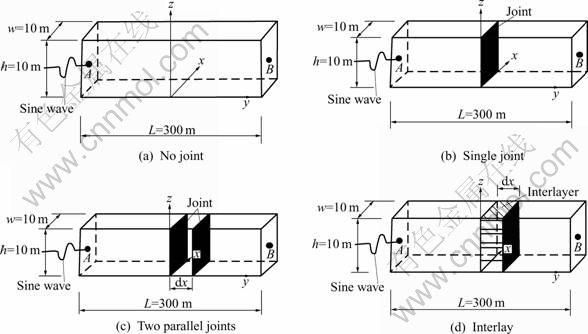
Fig.1 Sketches of distinct element models

Table 1 Mechanical properties of rock

2.2 Propagation of one-dimensional wave in rock mass containing a single joint

Wave transmission across a single joint is simulated to investigate the effect of a single joint on wave attenuation. It is known that reflection and transmission coefficients of normally incident wave on the single joint are dependent on frequency of wave and joint stiffness. It is assumed that deformation of joint is linearly elastic with constant stiffness during the propagation of elastic wave. It can be described as follows:

               　                    (1)

where for the normal deformation of the joint, Δu is the normal closure, σ is the average effective normal stress, and k is the normal stiffness; for the shear deformation of the joint, σ is the average effective shear stress, and k is the shear stiffness.

In the present study, propagations of one- dimensional P-wave and S-wave on a single joint with linearly elastic deformation are simulated by 3DEC. In 3DEC, the model is shown as Fig.1(b), which is obtained by introducing a single joint at y=0 m in Fig.1(a) with joint stiffness ranging from 1 GPa to 10 GPa. In order to avoid occurrence of frictional damage, the cohesive strength is set to the relatively high value. A sine P-wave and S-wave with the amplitude of 1 MPa is applied to the left boundary, y=-150. The wave frequency is 50 Hz. There are two measurement points at the positions before and after the joint to record the stress histories of the reflected and transmitted waves at the joint. One measurement point A is located at y=-140 m away form the joint, the other measurement point B is located at y=10 m closely after the joint. According to these records, the reflection and transmission coefficients can be calculated.

In the modeling computation, the joint stiffness is set to different values to obtain the reflection coefficient |R_i1|(i=1, 2) and transmission coefficient |T_i1| (i=1, 2) for the different values of the normalized stiffness of the joint, k/ωz, where ω is angular frequency, and z is the seismic impedance. For convenience, the following denotations are introduced. The transmission coefficient and reflection coefficient denote  |T_ij| (i=1, 2, j=1, 2, 3) and |R_ij|(i=1, 2, j=1, 2, 3), respectively. The subscript i and j represent respectively the type of wave and the type of discontinuity. When i is 1 or 2, it represents S-wave or P-wave. When j is 1, 2 or 3, it represents respectively that the discontinuity is a single joint, two parallel joints or interlay.

2.3 Propagation of one-dimensional wave in rock mass containing two parallel joints

Transmission of S-wave and P-wave across two parallel joints separated by different space is considered to study the effects of two parallel joints on the wave attenuation in terms of joint spacing. In computations, the normalized stiffness is constant and the transmission coefficient for wave transmission on two parallel joins is calculated as a function of the ratio ξ of joint spacing Δx to wavelength λ.

As shown in Fig.1(c), the first joint is fixed at y=0 m and the second joint is placed where the joint spacing is equal to λ/50, λ/20, λ/10, 3λ/20, λ/5, λ/4, 3λ/10, 7λ/20, 2λ/5, 9λ/20 and λ/20 m, separately. A sine P-wave and S-wave with the amplitude of 1 MPa is applied to the left boundary, y=-150. The wave frequency is 50 Hz. One measurement point A is positioned at y=-140 m to record the incident and reflected wave, the other measurement point B is placed closely after the second joint to record the transmitted wave. According to these records, the transmission coefficient  |T_i2| (i=1, 2) can be calculated.

2.4 Propagation of one-dimensional wave in rock mass containing interlay

In this section, propagation of sine P-wave in rock mass containing interlay is examined by considering the thickness of interlay d, seismic impedance z₁ and wave frequency f. It includes three stages. At the first stage, the effect of seismic impedance z₁ on propagation of P-wave is studied, when thickness d and frequency f keep constant. At the second stage, the effect of interlay d is conducted, when the seismic impedance z₁ and frequency f are constant. Finally, the effect of frequency f of P-wave is studied, when the thickness d and seismic impedance z₁ keep constant.

As shown in Fig.1(d), interlay is modeled by changing the material properties between two parallel joints. A sine P-wave with the amplitude of 1 MPa is applied to the left boundary, y=-150. The wave frequency is 50 Hz. Disposition of two measurement points is the same as that in the section of 2.3. According to these records, the transmission coefficient |T₂₃| can be calculated.

3 Simulated results and discussion

3.1 Simulating results on propagation of one- dimensional wave in intact rock

Based on the elastic wave theory, an elastic wave propagates through a continuous homogeneous, isotropic and elastic medium without wave attenuation. Fig.2(a) shows the shear stress histories at two measurement points A and B when a sine S-wave is applied at the left boundary in Fig.1(a) with the mesh size 5. Fig.2(b) shows the compressional stress histories at two measurement points A and B when a sine P-wave is applied at the left boundary in Fig.1(a) with the mesh size 5. It is obvious that waveforms recorded at point A and point B go all the way, thus, propagation of waves can be simulated accurately through 3DEC when the mesh size is reasonable. In the following computation, the maximum of mesh size is set to 5.

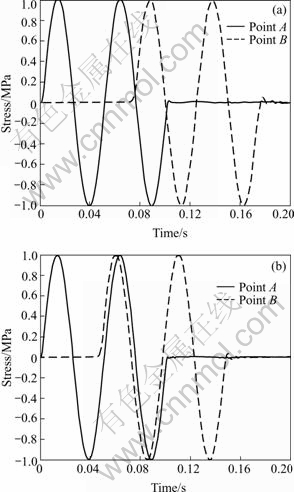
Fig.2 Waveforms recorded at points A and B: (a) Sine S-wave; (b) Sine P-wave

3.2 Effect of single joint on wave propagation

According to the displacement discontinuity theory, PYRAK-NOLTE[6] provided the analytic solutions of reflection coefficient and transmission coefficient of normally incident P-wave and S-wave on a single joint with linearly elastic deformation. For S-wave, expressions of reflection coefficient is

                        (2)

For P-wave, expressions of reflection coefficient is

                      (3)

For S-wave and P-wave, expressions of transmission coefficient is

()              (4)

The reflection coefficient and transmission coefficient can be calculated by equation (5) using the waveforms recorded at point A and point B.

，                            (5)

where A_I, A_R and A_T denote the amplitudes of incident wave, reflected wave and transmitted wave, respectively.

Fig.3(a) and (b) show the numerical results of reflection and transmission coefficients and theoretical solutions from PYRAK-NOTLE[6]. It is found that the numerical results agree well with the theoretical values.

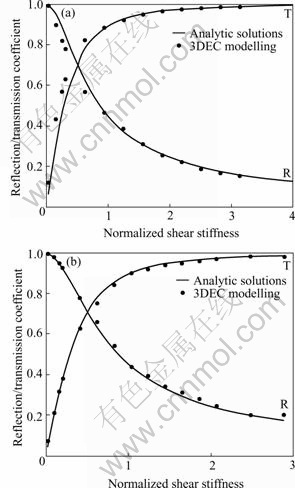
Fig.3 Comparison between modeling results and theoretical solutions of reflection and transmission coefficients for S-wave and P-wave across a single joint: (a) S-wave; (b) P-wave

3.3 Effect of two parallel joints on wave propagation

Similarly, according to the waveform recorded at point B, the transmission coefficients at two parallel joints are calculated. Fig.4(a) shows the numerical results of transmission coefficients and theoretical solutions from CAI and ZHAO[17] for normally incident S-wave, when k/ωz is equal to 0.62. It can be seen from Fig.4(a) that the modeling results agree with the theoretical results as a whole, while modeling results are slightly larger than the theoretical results. Fig.4(b) shows the numerical results of transmission coefficients for normally incident P-wave across two parallel joints. As seen from Fig.4(b), transmission coefficient |T₂₂| increases with the increasing ξ at first, then decreases with the increasing ξ, finally keep constant when ξ increases continuously.

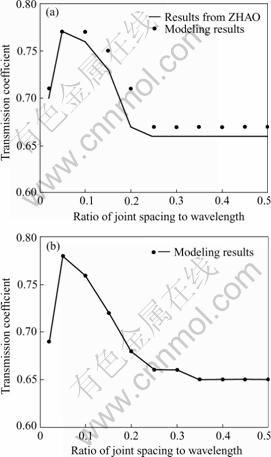
Fig.4 Comparison between 3DEC modeling results and theoretical solutions of transmission coefficients for S-wave and P-wave across two parallel joints: (a) S-wave; (b) P-wave

3.4 Effect of interlay on wave propagation

According to the elastic wave theory[25], we have

                             (6)

where  F is the reflection coefficient.

In Eq.(6), when z₁/z₀ is less than 1, compressional wave becomes tensile wave after it reflects at discontinuity. When z₁/z₀ is equal to 1, stress wave doesn’t reflect. When z₁/z₀ is more than 1, compressional wave remains compressional wave after it reflects at discontinuity. Fig.5 shows the recorded waveforms at points A and B when z₁/z₀ is set to different values. It is shown that the modeling results agree well with the theoretical results. When z₁/z₀ is equal to 0.32, reflected wave is out of phase. When z₁/z₀ is equal to 1, reflected wave hardly exists. When z₁/z₀ is equal to 3.2, reflected wave is in phase. However, transmitted wave is always in phase with incident wave regardless of z₁/z₀.

Figs.6(a), (b) and (c) show the waveform recorded at point A and point B when the incident wave frequency is 10 Hz, 50 Hz and 100 Hz and the thickness of interlay is 23.32 m and the seismic impedance is 0.32. For comparison, the transmitted wave is plotted in Fig.6(d) all together. As seen from Fig.6(d), the transmitted wave attenuates markedly and the attenuation increases with the increasing frequency. Furthermore, the phenomenon of leading phase occurs.

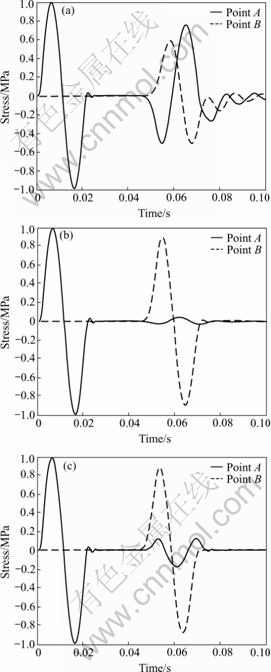
Fig.5 Waveforms recorded at point A and point B with different ratios of wave impedance: (a) z₁/z₀=0.32; (b) z₁/z₀=1; (c) z₁/z₀= 3.2

Fig.6 Waveforms recorded at point A and point B with variation of frequency: (a) f = 10 Hz; (b) f = 50 Hz; (c) f = 100 Hz;         (d) Transmitted wave when frequency is 10, 50 and 100, respectively

Fig.7 shows the waveforms recorded at point B when the incident wave thickness of interlay is 2.33 m, 23.32 m, 58.3 m and the frequency is 50 Hz and the seismic impedance is 0.32. For comparison, the incident wave is plotted in the same figure. Fig.8 shows the attenuation coefficient of transmitted wave with ratio of interlay thickness to wavelength. It can be seen from Fig.7 and Fig.8 that amplitude of transmitted wave decreases with the increasing thickness of interlay when seismic impedance and frequency are given.

Fig.7 Waveforms recorded at point B with variation of thickness

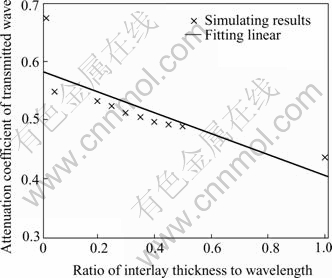
Fig.8 Attenuation coefficient of transmitted wave for ratio of interlay thickness to wavelength

4 Conclusions

Using the 3DEC to simulate one-dimensional normally incident wave propagation in rock mass containing no fracture, a single linear deformation fracture, two parallel linear fractures and interlay, the following conclusions can be drawn.

1) By comparison of the modeling results with the theoretical solutions, a good agreement between them has been achieved. It is verified that the 3DEC is capable of modeling one-dimensional wave propagation in rock masses.

2) Transmission coefficient |T₂₂| of normally incident compress ional wave across two parallel joints increases with the increasing ξ at first, then decreases with the increasing ξ, finally keep constant when ξ increases continuously.

3) When the incident wave propagates across the interlay, it attenuates markedly and the attenuation increases with the increasing frequency and thickness of interlay. Furthermore, the phenomenon of leading phase occurs.

References

[1] LI Xi-bing, GU De-sheng. Rock Impact Dynamics [M]. Changsha: Central South University of Technology Press, 1994. (in Chinese)

[2] LI Xi-bing. Influence of the structural weakness planes in rock mass on the propagation of stress waves [J]. Explosion and Shock Waves, 1993, 13(4): 334-342. (in Chinese)

[3] LI Xi-bing, GU De-sheng, LAI Hai-hui. Effect of interlay on the energy transmission of stress waves [J]. Non-ferrous Metals (Quarterly). 1993, 45(4): 1-6. (in Chinese)

[4] WU Y K, HAO H, ZHOU Y X, et al. Propagation characteristics of blast-induced shock waves in a jointed rock mass [J]. Soil Dynamics and Earthquake Engineering, 1998, 17(7-8): 407-412.

[5] HONG Hao, WU Yao-kun, MA Guo-wei, ZHOU Ying-xin. Characteristics of surface ground motions induced by blasts in jointed rock mass [J]. Soil Dynamics and Earthquake Engineering, 2001, 21(2): 85-98.

[6] PYRAK-NOLTE L J. The seismic response of fractures and the interrelations among fractures [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1996, 33(8): 787-802.

[7] KING M S, MYER L R, REZOWALLI J J. Experimental studies of elastic-wave propagation in a columnar-jointed rock mass [J]. Geophysics Prospecting, 1986, 34(8): 1185-1199.

[8] ZHAO X B. Theoretical and Numerical Studies of Wave Attenuation Across Parallel Fractures [D]. Singapore: Nanyang Technological University, 2004.

[9] SCHOENBERG M. Elastic wave behavior across linear interfaces [J]. Journal of Acoustic Society of America, 1980, 68(5): 1516-1521.

[10] MYER L R, PYRAK-NOLTE L J, COOK N G W. Effects of single fracture on seismic wave propagation [A]. Proceedings of ISRM Symposium Rock Joints[C]. Balkema, Rotterdam, 1990. 467-473.

[11] LEI W D, ASHRAF M H, ZHAO J. Pilot studies on two dimensional wave propagation in rock masses [J]. Trans Nonferrous Met Soc China, 2005, 15(4): 950-955.

[12] CROTTY J M, WARDLE L J. Boundary integral analysis of piecewise homogeneous media with structural discontinuities [J]. International Journal of Rock Mechanics and Mining Sciences & Geo-mechanics Abstracts, 1985, 22(6): 419-427.

[13] SCHWER L E, LINDBERG H E. Application brief: a finite element slide line approach for calculating tunnel response in jointed rock [J]. International Journal for Numerical and Analytical Methods in Geo-mechanics, 1992, 16: 529-540.

[14] CUNDALL P A. A computer model for simulating progressive large-scale movements in blocky rock systems [A]. Proceedings of Symposium of International Society of Rock Mechanics[C]. France: Nancy, 1971.

[15] LEMOS J V. A Distinct Element Model for Dynamic Analysis of Jointed Rock with Application to Dam Foundation and Fault Motion [D]. Minneapolis: University of Minnesota, 1987.

[16] BRADY B H, HSIUNG S H, CHOWDHURY A H, PHILIP J. Verification studies on the UDEC computational model of jointed rock [A]. Rossmanith H P. Mechanics of Jointed and Faulted Rock [C]. 1990. 551-558.

[17] CAI J G, ZHAO J. Effects of multiple parallel fractures on apparent attenuation of stress waves in rock masses [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(4): 661-682.

[18] CHEN S G, ZHAO J. A study of UDEC modeling for blast propagation in jointed rock masses [J]. International Journal of Rock Mechanics and Mining Sciences, 1998, 35(1): 93-99.

[19] CHEN S G, CAI J G, ZHAO J. Discrete element modeling of an underground explosion in a jointed rock mass [J]. Geotechnical and Geological Engineering, 2000, 18(2): 59-78.

[20] ZHAO J, CAI J G. Transmission of elastic P-waves across single fractures with a nonlinear normal deformational behavior [J]. Rock Mechanics and Rock Engineering, 2001, 34(1): 3-22.

[21] KULATILAKE P H S W, WANG S, STEPHANSSON O. Effect of finite size joints on the deformability of jointed rock in three dimensions [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1993, 30(5): 479-501.

[22] LI Shi-hai, GAO Bo, YAN Lin. 3-D simulation of the excavation of high steep slope of Three-Gorges permanent lock by distinct element method [J]. Rock and Soil Mechanics, 2002, 23(3): 272-277. (in Chinese)

[23] GUO Yi-yuan, LI Shi-hai, LIU Chun-tu. Application of Three-dimensional Discrete component method in the process of rock blasting [J]. Blasting, 2000, 17(S1): 19-23. (in Chinese)

[24] KUHLMEYER R L, LYSMER J. Finite element method accuracy for wave propagation problems [J]. Journal of Soil Mechanics and Foundation Division, ASCE, 1973, 99: 421-427.

[25] WANG Li-li. Fundamental of Stress Wave [M]. Beijing: National Defence Industry Press, 1985. (in Chinese)

Foundation item: Major projects(50490272, 50490274) supported by the National Natural Science Foundation of China; Project (2002CB412703) supported by the National Basic Research Program of China

Corresponding author: WANG Wei-hua; Tel: +86-731-8836628; E-mail: csuwwh@126.com

(Edited by PENG Chao-qun)