DOI: 10.11817/j.issn.1672-7207.2017.08.008
节点外啮合行星轮系耦合动力学分析及试验验证
鲍和云，谭在银，朱如鹏，陆凤霞
(南京航空航天大学 机电学院，江苏 南京，210016)
摘要：考虑太阳轮和行星架支承轴承的时变支承刚度，采用集中参数法建立节点外啮合行星齿轮系统齿轮-轴承耦合动力学模型，运用Rung-Kutta算法求解得到太阳轮和行星架的振动加速度响应；利用某型机械功率封闭试验台开展振动测试试验，基于小波变换获得降噪信号。研究结果表明：支承刚度时变情况下的振动加速度幅值要大于支承刚度为定值时的加速度。横向振动的试验值与理论值的误差为16.27%，在允许范围内，而纵向振动受重力影响存在较大偏差，同时，考虑时变支承刚度求解得到的振动加速度更接近试验结果，即支承刚度的时变性不可忽略。
关键词：节点外啮合；行星轮系；滚动轴承；耦合动力学；试验验证
中图分类号：TH132.413 文献标志码：A 文章编号：1672-7207(2017)08-2016-08
Theoretical and experimental analyses of coupling dynamics characteristic of planetary gear with meshing beyond pitc point
BAO Heyun, TAN Zaiyin, ZHU Rupeng, LU Fengxia
(College of Mechanical and Electrical Engineering,
Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
Abstract: Considering the time-varying support stiffness of bearings of the sun gear and the carrier, the lumped-parameter method was used to establish a coupling dynamics model of planetary gear transmission with meshing beyond pitch point. The vibration acceleration responses of the sun gear and the carrier were obtained by using Runge-Kutta method. The theoretical results show that the vibration acceleration values with time-varying support stiffness are larger than that with constant support stiffness. The experimental study using a mechanical power closed test rig was carried out. The experimental signals were denoised by the wavelet theory. There is an error of 16.27% between theoretical and experimental values in horizontal direction, which is in the allowed range; the values have large error in vertical direction due to the influence of gravity. The experiment results also show that the vibration acceleration values with the time-varying support stiffness are closer to the experimental results, which indicates that the time-variant of support stiffness is not ignorable.
Key words: meshing beyond pitch point; planetary gear; rolling element bearing; coupling dynamics; experiment
在普通齿轮啮合形式中，摩擦力在节点处发生换向造成系统内的冲击振动，通过采用节点外啮合，使得实际啮合线不经过节点，进而摩擦力在节点处不换向，减少了系统内的冲击振动，有效改善了系统的动力学特性。目前节点外啮合齿轮系统动力学方面已有不少的研究成果[1-4]，这些研究成果首先论述了节点外啮合的实现条件，进而以单对齿轮、行星齿轮的平移-扭转模型为研究对象，分析了节点外啮合对系统动力学特性的影响。但这些研究成果中轴承的支承刚度只是简单的处理成常量，并没有考虑时变性对传动系统动力学行为的影响，没能进一步揭示系统的动力学特性，且只是理论研究并没有得到试验验证。LIEW等[5-6]考虑了滚动轴承时变刚度对单级平行轴齿轮传动系统动力学行为的影响；周志刚等[7]考虑了滚动轴承时变刚度，分析了行星齿轮-轴承耦合动力学特性。虽然这些研究考虑了滚动轴承的影响，但系统中的齿轮副均是普通啮合，即非节点外啮合，在节点外啮合行星轮系中考虑轴承时变支承刚度，进一步揭示节点外啮合行星齿轮系统动力学特性的研究还少有报道。本文作者以节点外啮合行星轮系平移-扭转模型为研究对象，考虑滚动轴承时变支承刚度，建立齿轮-轴承耦合动力学模型，求解得到系统动态响应，并开展验证试验。
1 滚动轴承时变支承刚度计算
1.1 滚动轴承受力与变形关系
滚动轴承(本文以深沟球轴承为研究对象)由外圈、内圈、滚动体及保持架组成。假定内圈与旋转轴刚性连接，外圈与轴承座刚性连接，滚动体在内外圈之间等距排列，滚动体与滚道之间为纯滚动，则轴承变形主要是滚动体与滚道之间的接触变形。轴承受径向力的载荷分布如图1所示。
图1 滚动轴承载荷分布
Fig. 1 Load distribution of rolling bearing
由文献[8]可知：忽略轴承阻尼的影响，其径向力Fr和变形δr的关系为
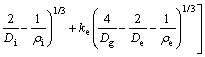(1)
式中：ki和ke分别为与轴承几何尺寸和材料等有关的系数；Dg为滚动体直径；Di为轴承内圈与滚动体接触处直径；De为轴承外圈与滚动体接触处直径；ρi为滚动体与内圈的接触曲率半径；ρe为滚动体与外圈的接触曲率半径；Z为受载滚动体数目。
1.2 时变支承刚度表达
将式(1)中系数整理合并后可得
(2)
式中：kH为Hertz接触刚度系数。则轴承支承刚度定义如下：
(3)
由式(3)可知：轴承支承刚度不是一个常量，会随着位移的变化而变化，具有时变性，滚动轴承因此可视为变刚度系数的硬弹簧[8]。
2 齿轮-滚动轴承耦合动力学模型
由于行星轮系相比定轴轮系，其结构更复杂，因此系统动力学模型也更为复杂，建立模型时采用如下假设：
1) 各行星轮具有相同的物理和几何参数，各方向上支承刚度相等。
2) 各齿轮均为渐开线直齿圆柱齿轮，支撑和轮齿简化为弹簧。
3) 各构件的运动保持在同一平面内。
4) 忽略齿侧间隙引起的非线性影响。
采用集中参数法，考虑太阳轮和行星架的滚动轴承时变支承刚度，忽略其余构件支承刚度的时变性，建立了节点外啮合行星齿轮传动系统动力学模型如图2所示(摩擦力和行星架横向、纵向支撑未表示)。
为便于方程的建立，在图中建立如下坐标系：OXY为定坐标系，原点位于行星架的回转中心，X轴通过第一个行星轮的理论中心；OnXnYn为动坐标系，与行星架固连并随行星架等速旋转，原点位于各行星轮理论中心On，两坐标轴分别与OXY坐标轴平行。图2中：x和y分别为构件的横向和纵向的平移自由度，u为构件的扭转自由度，因此，每个构件共有3个自由度，图示系统包括太阳轮、行星架、N个行星轮和内齿圈，因此该系统共有3N+9个自由度。由以上动力学模型，建立如下系统运动微分方程组：
(4)
式中：下标s，n，c和r分别为太阳轮、第n个行星轮、行星架和内齿圈；m和M分别为构件的质量和等效质量；ωc为行星架的旋转角速度；rb为构件的当量基圆半径；kx，ky和k0分别为构件横向、纵向上的支承刚度和扭转刚度；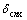
和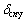
分别为行星架相对于第n个行星轮的位移沿行星架2个线位移方向的投影；
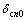为行星架相对于第n个行星轮沿行星架切线方向的投影。cx，cy和c0分别为构件横向、纵向上的支承阻尼和扭转阻尼；kpn和cpn分别为行星轮的支承刚度和支承阻尼；
；
，
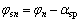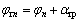为太阳轮和行星轮的啮合角，
为内齿圈和行星轮的啮合角，
为第n个行星轮的位置角；TD为输入转矩；TL为负载转矩。
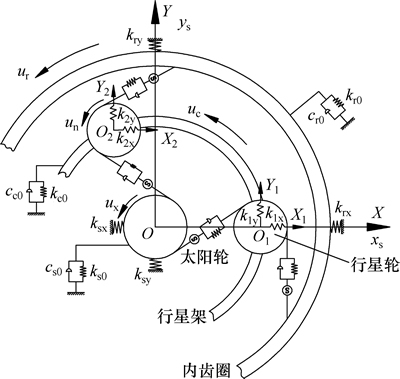
图2 节点外啮合行星齿轮系统平移-扭转模型
Fig. 2 Translational-rotational coupling dynamic model
考虑太阳轮和行星架的轴承支承，假设轴承内圈与轴固定，由式(3)可得时变支承刚度如下：
(5)
由式(5)可知：轴承支承刚度与齿轮中心振动位移有关，即二者之间存在耦合关系。
该系统齿轮副的重合度介于1和2之间，Fij (i为sn和rn；j=1，2)为齿轮副各对轮齿之间的啮合力：
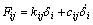(6)
式中：k为啮合刚度；c为啮合阻尼，计算方法见文献[9]；δ为啮合线上的相对位移。根据各啮合齿轮的相对位置关系，得到各相对位移表达如下：
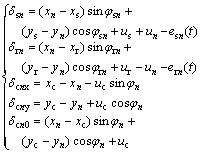(7)
式中：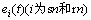
为轮齿间的综合啮合误差，一般假设综合啮合误差按正弦函数变化[9-10]，有
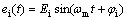(8)
式中：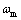
为齿轮啮合齿频；Ei为齿轮副i的综合啮合误差的幅值；
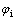这齿轮副的啮合初相位。
节点外啮合齿轮，由于实际啮合线不经过节点，因此摩擦力在节点处不换向，减少了冲击振动，这是节点外啮合的显著特点，上述系统运动微分方程中，由库伦定律，齿面滑动摩擦力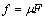
(其中，μ为摩擦因数，F为轮齿啮合力)。λ为摩擦力方向系数，是一个关于时间的函数，对于普通齿轮啮合，由文献[10]可知其函数式如下：
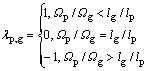(9)
式中：p和g代表1对啮合齿轮；Ωp和Ωg分别为两啮合齿轮在动坐标系中的角速度；lp和lg分别为两啮合齿轮的摩擦力臂。对于节点外啮合齿轮，在轮齿啮合过程中，λ 保持为1或-1，即摩擦力不换向。
在齿轮啮合过程中，摩擦因数随着啮合位置、润滑情况的不同而变化，但变化幅值不大，故在本文中将摩擦因数当作定值，取动摩擦因数μ=0.05[11]进行计算。
以上系统运动微分方程的矩阵形式如下：
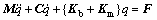(10)
式中：M为广义质量矩阵；C为阻尼矩阵；Kb为滚动轴承支承刚度矩阵；Km为齿轮啮合刚度矩阵；F为激励力矩阵；q为广义坐标列向量：
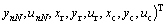(11)
3 实例计算
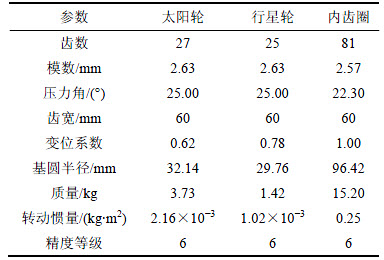
以某节点外啮合行星齿轮传动系统原理样机为例进行计算，主要参数如表1和表2所示，外啮合为普通啮合形式，内啮合为节点外啮合，行星轮个数N=3，系统功率P=25 kW，输入转速n=1 000 r/min。
太阳轮支承轴承型号为6213，行星架支承轴承型号为6020，具体参数如表1所示。
采用Rung-Kutta算法对系统运动微分方程组进行求解，得到稳定运转后太阳轮和行星架的振动加速度响应如下。
由表2可知：行星架的轴承尺寸要大于太阳轮的轴承尺寸，由式(1)~(3)可得输出端的支承刚度更大，因此，图3中行星架的振动加速度要小于太阳轮的振动加速度。图4中支承刚度的定值取时变支承刚度相同量级的值带入计算，可见支承刚度时变情况下的加速度更大一些。
图3 太阳轮和行星架的振动加速度
Fig. 3 Vibration accelerations of sun gear and carrier
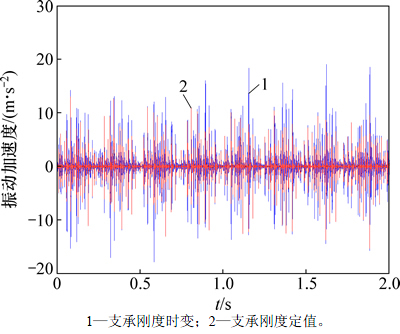
图4 时变支承刚度对振动加速度的影响
Fig. 4 Impacts of time-varying support stiffness on vibration accelerations
表1 滚动轴承主要几何参数
Table 1 Geometrical parameters of bearings
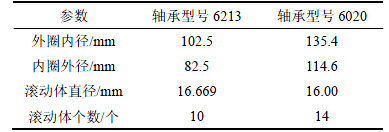
表2 节点外啮合行星齿轮系统主要参数
Table 2 Main parameters of planetary gear with meshing beyond pitch point
4 试验验证
振动测试试验通常在箱体外壁上布置加速度传感器，测量得到振动信号，以分析系统的振动特性。利用某机械功率封闭试验台，在太阳轮轴承座处布置加速度传感器，以获得齿轮系统振动信号，试验齿轮箱各部件参数与表1相同，行星轮个数N=3。
传感器型号为PCB356A26通用型三轴加速度传感器，可同时测量3个方向上的振动信号，信号采集系统为NI PXIe-1073，实际输入转速998 r/min，试验功率23.90 kW，采样频率fs=4 096 Hz，采样点数N=8 192。测量得到的原始信号如图5所示。
图5所示为测量得到的时域信号，对其作FFT变换得到图6所示频域信号。从频域上可见：啮合频率fm=337 Hz，信号中同时存在边频及高频噪音成分，无法直接用于验证理论分析结果，需要对原始信号进行消噪处理，目前，机械振动信号的消噪有多种方法[12-13]，其中小波变换对噪声消除有较好的效果[14]，因此得到了广泛应用。选择合适的小波基对信号进行小波分解，得到高频和低频分量，而噪声往往存在于高频分量，再通过设置合适的阈值，即可将高频分量去除，实现噪声消除。
目前常用的小波基有多种，需根据不同场合进行选择，其中Daubechies(dbN)小波系，经研究在实际应用中效果较好[15]，对图5中的原始信号采用db10小波进行2层分解，采用默认阈值消除高频分量，重构后得到如图7所示的去噪信号。
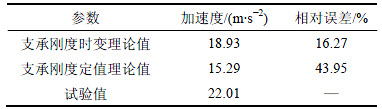
对比图5和图7可知：小波分析有效地去除了噪声影响，去噪信号的加速度幅值明显小于原始信号。对比图6和图8可知：原始信号中的边频带和高频成分大部分被滤除，剩余的频率成分主要为啮合频率，得到了较为干净的去噪信号，为了防止信号中有效成分丢失，并没有对原始信号进行过多的小波分解。由于重力的存在，使得y方向的振动受到影响，如图7所示，y方向的振动加速度要小于x方向，故取x方向对输入端太阳轮振动加速度最大值的理论值与试验值进行比较，其中理论值分别取支承刚度时变和定值2种情况，如表3所示。由表3可知：支承刚度时变情况下的理论值与试验值的相对误差为16.27%，由于理论模型在建立时采取了适当简化，与实际模型存在一定差距；系统动力学方程较为复杂，数值计算得到的是近似解；试验测量存在一定的系统误差等原因造成了该误差的存在，但属于允许范围，而支承刚度定值情况下的相对误差达到43.95%，说明同等条件下，支承刚度时变情况下的误差更小，加速度值更接近试验结果，即支承刚度的时变性不可忽略。
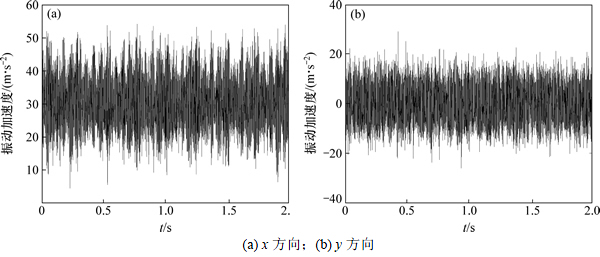
图5 输入端振动加速度原始信号
Fig. 5 Original signals of vibration accelerations for input
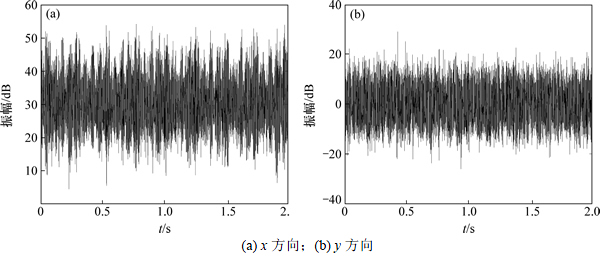
图6 原始信号的FFT变换
Fig. 6 FFT for original signals
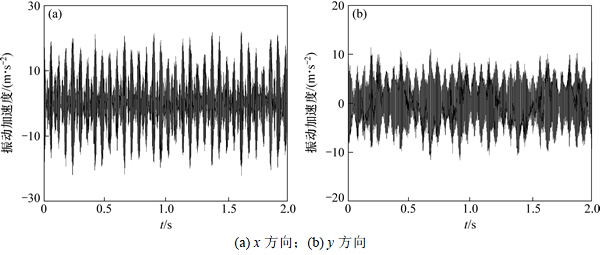
图7 输入端振动加速度去噪信号
Fig. 7 Denoised signals of vibration accelerations for input
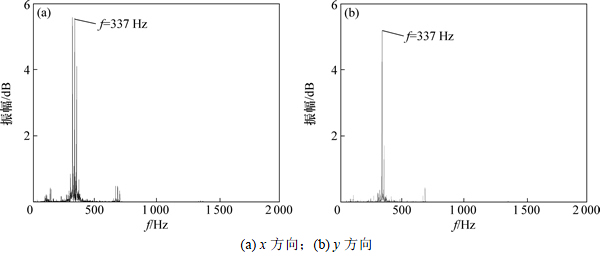
图8 去噪信号的FFT变换
Fig. 8 FFT for denoised signals
表3 理论值和试验值对比
Table 3 Comparison of theoretical values and experimental values
5 结论
1) 考虑输入、输出构件中滚动轴承时变支承刚度，采用集中参数法建立节点外啮合行星齿轮系统耦合动力学模型，模型包含3N+9个自由度，进一步完善节点外啮合行星轮系的理论分析模型。
2) 采用Rung-Kutta算法求解得到输入、输出构件的振动加速度响应，揭示了支承刚度时变情况下的节点外啮合行星轮系的动力学特性，对比分析支承刚度时变和支承刚度定值2种情况下的振动加速度响应，结果表明支承刚度时变情况下的振动加速度幅值更大。
3) 利用某机械功率封闭试验台开展了验证试验，基于小波变换对原始信号进行处理获得了较好的消噪信号，试验结果表明y方向的振动受重力影响，振动加速度小于x方向；x方向上理论值与试验值的误差为16.27%，在允许范围内，理论分析结果得到了较好的验证；同时，支承刚度时变与定值2种情况下，前者的加速度更接近试验结果，表明支承刚度的时变性不可忽略。
参考文献：
[1] 郑增铭, 柳青松. 少齿数渐开线齿轮节点外啮合的判定条件[J]. 兰州工业高等专科学校学报, 2004, 11(3): 13-15.
ZHENG Zengming, LIU Qingsong. The judgment condition for the involute gear pair with fewer teeth number outside pitch point[J].Journal of Lanzhou Polytechnic College, 2004, 11(3): 13-15.
[2] 田静云, 王保民, 张国海. 渐开线圆柱齿轮出现节点外啮合的研究[J]. 陕西理工学院学报(自然科学版), 2007, 23(2): 5-7.
TIAN Jingyun, WANG Baomin, ZHANG Guohai. Study of involutes cylindrical gear-pair’s emerging node external gearing[J]. Journal of Shaanxi University of Technology (Science and Technology), 2007, 23(2): 5-7.
[3] 刘晶晶. 节点外啮合齿轮副设计方法及动力学分析[D]. 南京: 南京航空航天大学机电学院, 2012: 56-63.
LIU Jingjing. Design method and dynamics analysis of node external gear-pair[D]. Nanjing: Nanjing University of Aeronautics and Astronautics. College of Mechanical and Electrical Engineering, 2012: 56-63.
[4] 孙永正. 节点外啮合行星齿轮传动系统设计方法及动力学分析[D]. 南京: 南京航空航天大学机电学院, 2013: 54-62.
SUN Yongzheng. Design methods and dynamic analysis of planetary gear transmission drive with meshing beyond pitch point[D]. Nanjing: Nanjing University of Aeronautics and Astronautics. College of Mechanical and Electrical Engineering, 2013: 54-62.
[5] LIEW H V, LIM T C. Analysis of time- varying rolling element bearing characteristics[J]. Journal of Sound and Vibration, 2005, 283(3): 1163-1179.
[6] SAWALHI N, RANDALL R B. Simulating gear and bearing interactions in the presence of faults (Part I): The combined gear bearing dynamic model and the simulation of localised bearing faults[J]. Mechanical Systems and Signal Processing, 2008, 22(8): 1924-1951.
[7] 周志刚, 秦大同, 杨军, 等. 变载荷下风力发电机行星齿轮传动系统齿轮-轴承耦合动力学特性[J]. 重庆大学学报(自然科学版), 2012, 35(12): 7-14.
ZHOU Zhigang, QIN Datong, YANG Jun, et al. Gear-bearing coupling dynamics characteristics of wind turbine planetary gear transmission system under variable load[J]. Journal of Chongqing University (Natural Science), 2012, 35(12): 7-14.
[8] 何芝仙, 干洪. 计入轴承间隙时轴-滚动轴承系统动力学行为研究[J]. 振动与冲击, 2009, 28(9): 120-124.
HE Zhixian, GAN Hong. Dynamic behavior of a shaft-rolling bearing system with clearance[J]. Journal of Vibration and Shock, 2009, 28(9): 120-124.
[9] 李润方, 王建军. 齿轮系统动力学-振动冲击噪声[M]. 北京: 科学出版社, 1997: 160-161.
LI Runfang, WANG Jianjun. Gear system dynamics- vibration impact & noise[M]. Beijing: Science Press, 1997: 160-161.
[10] 朱恩涌, 巫世晶, 王晓笋, 等. 含摩擦力的行星齿轮传动系统非线性动力学模型[J]. 振动与冲击, 2010, 29(8): 217-220.
ZHU Enyong, WU Shijing, WANG Xiaosun, et al. Nonlinear dynamics model of planetary gear with friction[J]. Journal of Vibration and Shock, 2010, 29(8): 217-220.
[11] 石莹, 江亲瑜, 李宝良. 基于虚拟样机技术的渐开线齿轮啮合摩擦动力学研究[J]. 润滑与密封,2011, 36(7): 32-35.
SHI Ying, JIANG Qinyu, LI Baoliang. Research on friction dynamics of involute gear meshing based on virtual prototyping technology[J]. Journal of Lubrication Engineering, 2011, 36(7): 32-35.
[12] 何清波, 孔凡让, 朱忠奎, 等. 盲卷积分离及其在机械振动信号消噪中的应用研究[J]. 振动与冲击, 2006, 25(2): 30-34.
HE Qingbo, KONG Fanrang, ZHU Zhongkui, et al. Blind sources separation for convolutive mixtures and its applications in mechanical vibration noise elimination[J]. Journal of Vibration and Shock, 2006, 25(2): 30-34.
[13] 王成栋, 朱永生, 张优云. 转子振动信号消噪方法的研究[J]. 振动、测试与诊断, 2003, 23(4): 252-255.
WANG Chengdong, ZHU Yongsheng, ZHANG Youyun. Study on denoising rotor vibration signals contaminated by electromagnetic interference[J]. Journal of Vibration, Measurement & Diagnosis, 2003, 23(4): 252-255.
[14] 胡俊文, 周国荣. 小波分析在振动信号去噪中的应用[J]. 机械工程与自动化, 2010, 2(1): 128-130.
HU Junwen, ZHOU Guorong. Application of wavelet analysis in vibration signal denoising[J]. Mechanical Engineering & Automation, 2010, 2(1): 128-130.
[15] 郭亚. 振动信号处理中的小波基选择研究[D]. 合肥: 合肥工业大学机械与汽车工程学院, 2003: 16-18.
GUO Ya. Research on wavelet base selection for vibration signal processing[D]. Hefei: Hefei University of Technology. School of Machinery and Auto mobile Engineering, 2003: 16-18.
(编辑 陈爱华)
收稿日期：2016-09-22；修回日期：2016-12-30
基金项目(Foundation item)：国家自然科学基金资助项目(51305196)(Project(51305196) supported by the National Natural Science Foundation of China)
通信作者：鲍和云，博士，副教授，从事机械CAD及自动化研究；E-mail：siyanger@163.com
