DOI: 10.11817/j.issn.1672-7207.2016.02.014

不同地应力下TBM盘形滚刀破岩特性

夏毅敏^{1, 2}，吴才章¹，顾健健¹，丛国强¹，唐露¹，张魁¹

 (1. 中南大学 机电工程学院，湖南 长沙，410083；

2. 中南大学 高性能复杂制造国家重点实验室，湖南 长沙，410083)

摘要：根据Mohr-Coulomb准则分析岩石强度与地应力的变化关系，对不同地应力下盘形滚刀破岩载荷模型进行修正；以锦屏二级水电站TBM掘进现场实测的数据为依据，建立有初始地应力和无初始地应力下盘形滚刀破岩仿真模型，并进行无初始应力滚刀破岩试验，研究盘形滚刀破岩载荷特性及岩石破碎特征。研究结果表明：随着地应力的增大，三向力载荷增大；在各个贯入度下，初始应力为28~36 MPa时与0 MPa时相比，垂直力和滚动力的增加幅度较大，增大幅度可达到70%以上，侧向力增加幅度最小；随着初始地应力的增加，滚刀总破岩量减少，破岩能耗上升；三向力理论计算值与仿真值吻合较好，相对误差范围在10%~21%之间；无初始应力下的破岩试验在一定程度上验证力学模型和仿真结果的正确性。

关键词：地应力；盘形滚刀；力学模型；贯入度；三向力载荷

中图分类号： U455.3⁺1             文献标志码：A         文章编号：1672-7207(2016)02-0450-09

Mechanical characteristics of TBM disc cutter under the initial stress

XIA Yimin^{1, 2}, WU Caizhang¹, GU Jianjian¹, CONG Guoqiang¹, TANG Lu, ZHANG Kui¹

 (1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;

2. State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China)

Abstract: According to Mohr-Coulomb strength standard, the relationship between strength of rock and initial stress was analyzed and the rock-craking load model of disc cutter in the environment of initial stress was revised. Based on the excavating condition of TBM in Jinping secondary hydropower station, the rock-breaking simulation model under initial stress or not was established and the rock-breaking experiment without initial stress was carried out to study the load characteristic of disc cutter and the rock-breaking characteristic. The results show that the three-dimensional force increases with the increase of the initial stress; at a certain penetration depth, when the initial stress is 28-36 MPa, the vertical force and rolling force increase by a bigger margin with a rate of more than 70%, and the lateral force increases by the smallest margin compared with that of 0 MPa. With the increasement of initial stress, the total quantity of cracked rock decreases, and the energy consumed in breaking rock increases. The theoretical value and the simulation value of the three-dimensional force can fit well and the relative error of three-dimensional force ranges from 10% to 21%. The rock-craking load model and the simulation results can be verified to some extent by the rock-breaking experiment without initial stress.

Key words: initial stress; disc cutter; mechanical model; penetration depth; three-dimensional force load

全断面岩石掘进机(TBM)是硬岩隧道施工中的重要掘进装备，掘进过程中地应力影响较大，并且随着埋深的增大，地应力变大。拉西瓦水电站^[1]地下厂房洞室群最大地应力达到29.7 MPa，锦屏一级水电站^[2]地下厂房区最大地应力值达37.5 MPa，锦屏二级水电站^[3]的引水隧洞群在长探洞中实测最大地应力高达42.4 MPa。在不同地应力下岩石特性变化较大，与盾构盘形滚刀破岩相比，岩石破碎特征和刀具载荷特性出现很大差异。目前，在岩石破碎特征和载荷方面，谭青等^[4-5]基于颗粒离散元法建立不同切削顺序和不同节理特征下盘形滚刀破岩的数值模型，研究滚刀受力和岩石应力分布状态。在地应力下岩石力学特性的研究方面，HAIMSON等^[6]通过真三轴加载试验对岩石的力学性能和强度准则进行了研究；刘泉声等^[7]对花岗岩进行了不同围压下的三轴加压实验，研究了试样的变形规律和强度变化特征，得到岩石三轴抗压强度和抗剪强度近似遵循Mohr-Coulomb强度准则的变化规律。在TBM盘形滚刀的载荷特性研究方面，国内外学者^[8-12]。对滚刀破岩过程进行了大量实验研究和数值模拟分析，并提出了相应的力学计算模型和载荷变化规律。龚秋明等^[13]开展了大量TBM掘进试验测试，基于现场实测数据对高地应力作用下岩体可掘性指数的变化进行了分析，提出了TBM的运行要与地应力条件相匹配。在实际地应力环境下的盘形滚刀在破岩过程中，岩石掌子面不受初始地应力，而岩石的侧面不同方向承受不相等的地应力，而且可能差异很大，这将会对盘形滚刀与岩石耦合作用特性造成很大影响。本文作者基于Mohr-Coulomb强度准则对滚刀破岩力学模型进行修正，通过建立有限元仿真模型对初始地应力下盘形滚刀破岩过程进行模拟，研究岩石的破碎特征与刀具的载荷变化特性。

1  不同地应力下盘形滚刀力学模型研究

1.1  不同地应力下岩石强度特性研究

根据Mohr-Coulomb强度准则^[14]，当材料某平面上剪应力τ达到某一特定值时，材料发生屈服。并且该特定值不是一个常数，而与该平面上的正应力σ相关，其强度准则模型关系如图1所示。

分析图1中各个参数间存在的关系，可将Mohr-Coulomb强度准则^[14]表示为

             (1)

其中剪切面上的正应力σ和剪应力τ有以下关系：

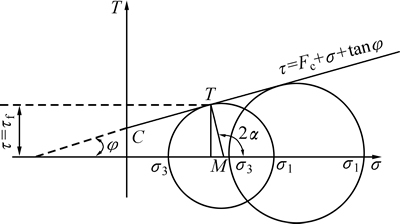
图1  莫尔-库伦准则

Fig. 1  Mohr-Coulomb standard

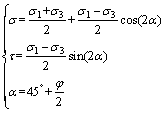         (2)

对式(1)和(2)进行联立并推导，可以得到岩石轴向抗压强度和抗剪强度随地应力变化的理论关系式：

         (3)

式中：σ_c为岩石单轴抗压强度；φ为岩石内摩擦角；σ₃为岩石侧面最小主应力；σ₁为地应力下的轴向抗压强度；τ为岩石抗剪强度；F_c为岩石内聚力；σ为剪切面上的正应力。

1.2  不同地应力下盘形滚刀力学模型的建立

盘形滚刀在破岩过程中主要受到如图2所示的载荷F₁，F₂和F₃，将3个载荷直角分解得到下式：

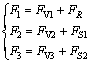               (4)

其中：F_V1，F_V2和F_V3为垂直力的3个分量；F_S1和F_S2为侧向力的2个分量；F_R为滚动力。

对上述载荷进行分别合成，可以得到盘形滚刀的垂直力、滚动力以及侧向力载荷，如下式所示：

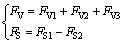             (5)

根据挤压与剪切破坏理论可知：F_V1主要与挤压破碎面积在垂直方向上的投影面积与岩石抗压强度有关；F_V2和F_V3是由相邻滚刀间岩石发生崩碎时所需要的垂直力，其值与F_S1和F_S2成角度关系；F_S1和F_S2为岩石发生侧向剪切破坏的剪切力，其值为抗剪强度τ与剪切面积的乘积；F_R为刀盘切向滚动的切割力。在假设相邻滚刀间岩石完全破碎基础上，XIA等^[15]提出了一个无地应力工况下考虑盘形滚刀的安装半径、相位角、刀间距及滚刀刀圈结构参数的盘形滚刀受力计算模型。

图2  盘形滚刀受力分析

Fig. 2  Force analysis of disc cutter

在不同地应力作用下，岩石抗压强度和抗剪强度发生改变，进而滚刀的三向力载荷也随之改变。基于无地应力下的三向力模型^[15]，结合岩石抗压强度、抗剪强度与最小主应力σ₃的关系式(3)，得到修正后考虑初始地应力的盘形滚刀受力模型，如下式所示：

(6)

式中：R为滚刀半径；r为刀刃过渡圆弧半径；B为滚刀刀刃顶部宽度；f为滚刀与岩石的接触角，；θ为刀圈半刃角；τ为岩石的抗剪强度；s为刀间距；R_i为第i把盘形滚刀在刀盘上的安装半径；β₁为所讨论滚刀与其内侧滚刀间因相位差造成的岩面倾角；β₂为所讨论滚刀与其外侧滚刀间的岩面倾角；h为滚刀贯入度(刀盘旋转1周所推进的深度，在掘进过程中可认为是盘形滚刀的切深)。

2  盘形滚刀破岩仿真建模

锦屏二级水电站工程1号引水隧洞岩石单轴抗压强度为73.64 MPa，埋深约为1 800 m，根据地应力文献[16]，经回归分析后试验点X，Y和Z方向地应力分别约为28，28和36 MPa。3号引水隧洞岩石单轴抗压强度为105 MPa，埋深约为1 300 m，根据文献[16]，回归后X，Y和Z 方向地应力分别约为20.5，23.0和31.0 MPa。

仿真中给岩石四周施加不同垂直侧面的初始应力载荷σ₂和σ₃。与滚刀接触的掌子面不施加初始应力载荷，岩石底面施加全约束，两把盘型滚刀顺次侵入岩石一定深度后绕中心轴以恒定角速度回转。数值模拟过程中记录盘形滚刀的垂直力、侧向力、滚动力以及岩石的破碎特征。

根据锦屏二级水电站TBM掘进情况，刀具为直径432 mm滚刀，岩石选用单轴抗压强度为108.05 MPa的大理岩，测试确定相关力学参数，如表1所示。仿真模拟不同初始地应力和贯入度下滚刀破岩过程，贯入度为模拟过程中滚刀侵入岩石表面保持的深度，仿真参数如表2所示。根据实测的地应力数据^[16]，确定岩石侧面所受的初始水平主应力σ₂和σ₃，如表3所示。

表1  大理岩材料参数

Table 1  Material parameter of marble in Jinping

表2  模拟方案参数

Table 2  Parameter of simulant project

表3  岩石的初始应力水平

Table 3  Initial stresses level of rock

3  模拟结果分析

3.1  初始地应力下的岩石破碎特征

大理岩在地应力环境下其力学性能发生改变，在盘形滚刀的作用下其破碎特性同样发生明显变化，取6 mm贯入度下的相同时间步分析不同应力对破岩的影响形式，各个工况的mises应力特征如图3所示。以截面上第2把滚刀切削破碎的岩石单元数量作为参考，对截面上的滚刀正下方破岩面积和滚刀两侧破岩面积进行划分和计算，值如表4所示。

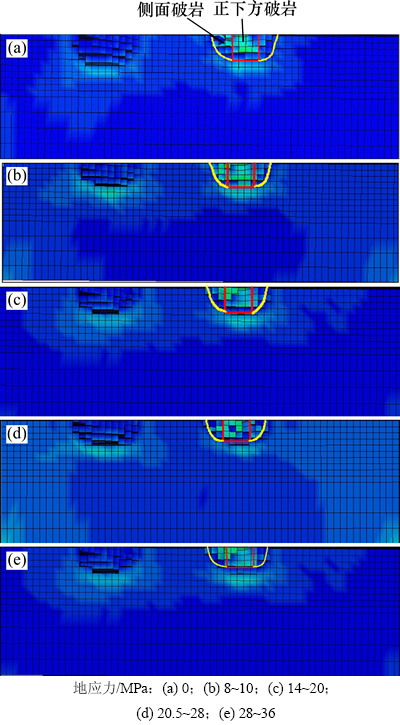
图3  6 mm贯入度的相同时间步下的各工况破碎截面

Fig. 3  Racking section in different working condition under penetration depth of 6 mm and same time-step

表4  不同初始应力下的破岩面积

Table 4  Rock-cracking area under different initial stress

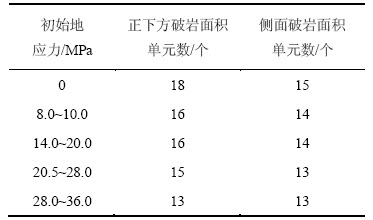
根据破岩面积的统计结果绘制其变化曲线，结果如图4所示。分析图3和图4可知：在盘形滚刀贯入度不变的情况下，随着岩石四周初始应力的增加，盘形滚刀正下方的破岩面积逐渐减少，6 mm贯入度下28~36 MPa较0 MPa时减少了27.8%，这是由于随着初始应力的增加，岩石的强度变大，造成刀刃正下方更加不易破碎；随着初始地应力的增加，滚刀刀刃两侧的破碎面积也逐渐减少，6 mm贯入度下28~36 MPa较0 MPa时减少了13.3%，减小幅度相对较小。一方面，由于地应力的存在，岩石强度增大，侧向岩石破碎困难增大；另一方面，在滚刀对岩石的侧向剪切与地应力对岩石的侧向挤压的共同作用下，岩石侧向弹性应变能向凌空的掌子面释放，滚刀刀刃两侧岩石易向掌子面发生破碎，其状态如图5所示，因此造成在滚刀载荷上升的同时，滚刀两侧的岩石破碎量减少幅度要小于滚刀正下方的；总的破岩量随地应力的增大而减少，6 mm贯入度下28~36 MPa较0 MPa时减少了21.2%，然而滚刀的破岩载荷上升很大，表明初始应力的存在，造成滚刀的破岩能耗上升，岩石更加不易发生破碎。

TBM在掘进过程中盘形滚刀以固定的贯入度绕着刀盘中心轴做回转运动，其破岩量(V)可以近似认为是截面的破岩面积(S)与滚刀破岩弧长(l)的乘积，即V=S×l，在刀盘回转速度保持不变的情况下，相同时间内滚刀的破岩弧长保持不变，进而破岩体积与截面破岩面积成正比，具有相同的变化规律。

3.2  盘形滚刀破岩力变化规律

图6所示为20.5~28 MPa初始应力，8 mm贯入度工况的三向力载荷随着时间变化关系。由图6可以发现：滚刀与岩石发生接触，滚刀载荷开始上升，随着滚刀的不断前进，岩石发生塑性应变被压实，滚刀载荷不断上升，当岩石发生破碎时，滚刀载荷突然下降，完成一次破碎过程，随着滚刀的继续前进，上述破岩过程反复发生，呈现典型的阶跃破碎过程；随着盘形滚刀的向前滚压，其滚动方向与垂直方向岩石同时受到滚刀载荷，其破碎过程一致，进而滚动力与垂直力变化规律相似；盘形滚刀两侧都受到侧向载荷作用，因载荷方向相反而相互抵消，进而造成其合力值相对较小；盘形滚刀做回转运动，其内外侧岩石的破碎过程不一致，造成其载荷有内外侧方向上的波动，而且侧向力的平均值由滚刀内侧指向外侧。

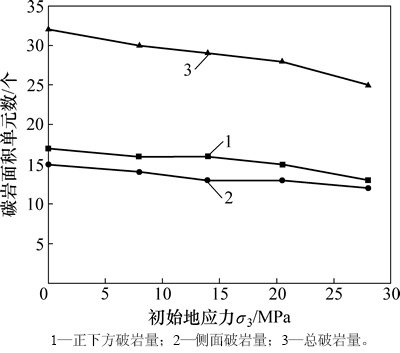
图4  破岩面积随着初始应力的变化关系

Fig. 4  Changing relationship between rock-cracking area and initial stress

图5  两侧向自由面破碎图

Fig. 5  Rock-cracking diagram of two side free surface

对各工况下的破岩载荷进行统计并绘制其变化关系，进一步分析三向力载荷的变化规律。

3.2.1  垂直力变化特征

图7所示为垂直力与初始应力、贯入度的变化关系曲线。由图7可知：垂直力随着初始应力的增加而增加，增加幅度小幅减小；随着贯入度的增加，初始应力与垂直力的关系曲线的斜率略有上升，表明在低贯入度时，初始应力对载荷的影响作用率相对较小，随着贯入度的增加，刀具与岩石的接触越大，造成初始应力对载荷的影响效应增强；在各个贯入度下初始应力在28~36 MPa时较0 MPa时垂直力载荷增加了53.6~108.6 kN，增加幅度为63.5%~71.4%。

图6  三向力载荷随着时间变化关系

Fig. 6  Changing relationship between three-dimensional force and time

图7  垂直力与初始应力、贯入度的变化关系

Fig. 7  Changing relationship between vertical force,initial stress and penetration depth

3.2.2  滚动力变化特征

图8所示为滚动力与初始应力σ₃、贯入度的变化关系曲线。由图8可知：滚动力随着初始应力的增加而增加，增加幅度逐渐较小；随着贯入度的增加，初始应力与滚动力的关系曲线的斜率略有上升，其变化规律的原因与垂直力的变化规律原因一致；在各个贯入度下初始应力在28~36 MPa时较0 MPa时增加了5.3~11.2 kN，增加幅度为56.0%~73.6%；滚动力的变化规律与垂直力的变化规律比较相似，进而可近似认为滚动力与垂直力呈线性关系。

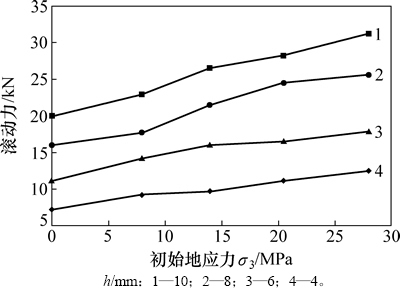
图8  滚动力与初始应力、贯入度的变化关系

Fig. 8  Changing relationship between rolling force, initial stress and penetration depth

3.2.3  侧向力变化特征

图9所示为侧向力与初始应力σ₃、贯入度的变化关系曲线。由图9可知：侧向力随着初始应力的增加而增大；随着贯入度的增加，侧向力大幅度增加，其增幅明显高于垂直力和滚动力的增幅，这是由于随着贯入度的增加，盘形滚刀两侧的破岩面积增大，并且增加幅度逐渐变大；在各个贯入度下，初始应力为28~36 MPa时较0 MPa时增加了0.32~2.50 kN，增加幅度为48.4%~62.4%，侧向力载荷和增加幅度相对垂直力和滚动力较小，这是由于两侧破岩力随着初始应力增加都会增大，而侧向力是由滚刀两侧破岩力相减得到的，进而增加幅度相对较小。

图9  侧向力与初始应力、贯入度的变化关系曲线

Fig. 9  Changing relationship between lateral force, initial stress and penetration depth

综上所述，在相同的贯入度下，随着应力的增加，盘形滚刀受到的载荷随之增加，表明由于初始地应力的作用，岩石发生了强化，需要更大的载荷才能使之发生破碎。为达到理想的施工进度，锦屏二级水电站施工中途采用能承受更大推力的直径为483 mm的滚刀进行施工，以保证正常的贯入度掘进，提高施工效率，此施工情况与仿真结果相符。

3.3  仿真载荷与理论计算值对比分析

地应力下的盘形滚刀破岩实验尚无条件进行，而有限元的破岩过程模拟是一种常用方法，将仿真载荷与理论模型载荷进行对比分析。

图10所示为不同初始应力和贯入度下仿真值与理论值的对比。由图10可知：仿真值和理论计算结果变化趋势一致。贯入深度为8和10 mm时，三向力载荷仿真值偏小于理论值，这是由于仿真设置单元达到一定应力会消失来模拟岩石被压实突然破碎的过程，在贯入度大的情况下，岩石单元消失使载荷增大到一定程度就会下降。垂直力的仿真值和理论值的最大差值为30.45 kN，最大相对误差率为10.2%；滚动力与垂直力的变化趋势基本一致，仿真值与理论值的最大差值为3.0 kN，最大相对误差为12.4%；侧向力随着初始应力的增加而增加，且随着贯入度的增加，增加幅度明显上升，仿真值与理论值的最大差值为2.11 kN，最大相对误差为21.1%。通过分析发现，在0 MPa到28~36 MPa应力范围内修正的初始应力下的力学模型计算值与仿真值的最大相对误差为21.1%，一定程度上能够较好地反应盘形滚刀破岩的三向力特性及其变化趋势。

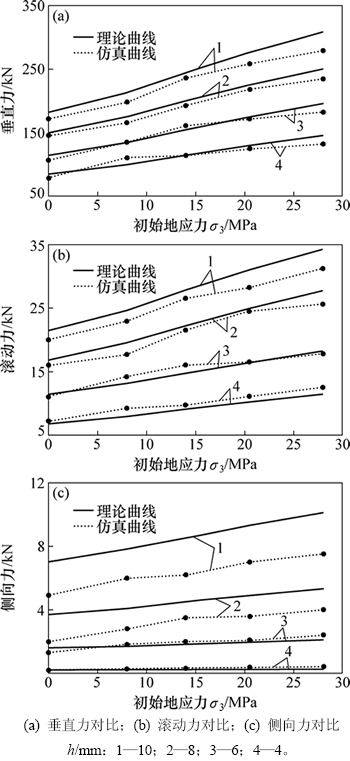
图10  不同初始应力和贯入度下仿真值与理论值对比

Fig. 10  Comparison between numerical simulant value and theoretical value under different initial stresses and penetration depths

4  试验验证

4.1  试验方案

在盘形滚刀切削性能试验台上进行无初始应力不同贯入度下的破岩试验，选用岩石与仿真岩石的参数一致，贯入度设置为6，8和10 mm。试验过程如下：滚刀侵入岩石一定深度后，再直线进给切削岩石，完成1次切削后，横向移动岩石，重复切削。为了验证仿真方法和边界条件设置的合理性，重新建立了无初始应力下的仿真模型，与理论值、试验值进行对比   验证。

4.2  试验分析

4.2.1  岩石的宏观破碎现象分析

按上述试验方案进行试验，盘形滚刀滚压破岩时的宏观破碎过程如图11所示。从图11可以看出：随着滚刀不断向前滚压，刀刃不断压入新鲜岩石，与刀刃接触部分岩石被压碎而形成岩粉喷出。同时，压碎区向外产生挤压作用，在刀刃两侧产生裂纹，随着挤压作用逐渐加大，裂纹不断扩展，直至岩块形成而剥离。

图11  滚压破岩的宏观破碎过程

Fig. 11  Macro fracture process of rolling rock-breaking

4.2.2  破岩载荷分析

切削速度为10 mm/s、贯入度为8 mm时，滚压破岩过程中滚刀所受载荷如图12所示。由图12可见：5~10 s为滚压切削阶段，破岩力有明显的上升和回落的锯齿状波动过程，垂直力在123 kN上下波动，而滚动力在22.5 kN上下波动。

4.3  试验载荷、仿真载荷与理论计算值对比分析

图13所示为无初始应力不同贯入度下的破岩载荷试验值、仿真值与理论计算值的对比。试验中滚刀沿着直线切削破岩，无法模拟真实情况下滚刀回转承受侧向力的实际工况，所以无法对比侧向力的情况。由图13(a)可知：垂直力的试验值和理论值的最大差值为26.9 kN，最大相对误差率为17.9%；垂直力的试验值和仿真值的最大差为32.3 kN，最大相对误差为20.3%；由图13(b)可知：滚动力的试验值、仿真值和理论值变化趋势基本一致，理论值和仿真值比较吻合，试验值相比偏大，最大差为5.7 kN，最大相对误差为25.3%；通过分析发现，在无初始应力下，修正的力学模型计算得到的载荷与试验值的最大相对误差为25.3%，破岩试验在一定程度上验证了力学模型和破岩仿真的正确性和准确性。

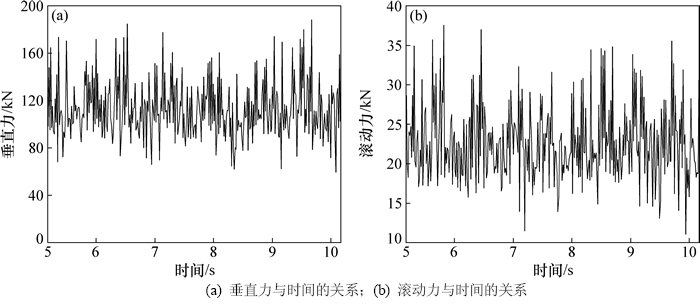
图12  滚刀破岩力

Fig. 12  Rock-craking load of dis cutter

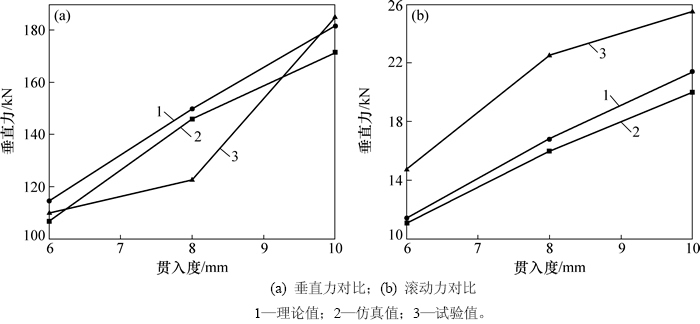
图13  试验载荷、仿真载荷与理论载荷对比

Fig. 13  Comparison between experiment value ,numerical simulant value and theoretical value

5  结论

1) 根据地应力下岩石力学特性的变化特征，建立了考虑初始地应力的盘形滚刀回转三向力模型。

2) 建立有地应力、无地应力下的盘形滚刀破岩过程的仿真模型，并进行了无围压下滚刀破岩试验，对理论计算载荷、仿真结果与试验结果进行对比，在一定程度上验证了三向力模型与仿真结果的合理性。

3) 盘形滚刀的三向力载荷呈现典型的阶跃特性，在相同贯入度下，三向力载荷随着初始应力的增加而增大，增加的幅度随初始应力增加幅度略有减小；在相同初始应力下，三向力载荷随着贯入度的增加而增大，其中垂直力和滚动力的增加幅度变化较小，侧向力的增加幅度逐渐增大；在各个贯入度下，初始应力在28~36 MPa时较0 MPa时垂直力载荷增加幅度为63.5%~71.4%，滚动力增加幅度为56.0%~73.6%，侧向力增加幅度为48.4%~62.4%。

4) 在贯入度不变的情况下，随着初始应力的增加，滚刀正下方岩石破碎下逐渐减少；滚刀两侧岩石的破岩面积也有所减少，减少幅度较小；总破岩量减少，破岩能耗逐渐变大。

参考文献：

[1] 姚显春, 李宁, 曲星, 等. 拉西瓦水电站地下厂房三维高地应力反演分析[J]. 岩土力学, 2010, 31(1): 246-252.

YAO Xianchun, LI Ning, QU Xing, et al. Back analysis of three- dimensional initial geostress Laxiwa underground powerhouse[J]. Rock and Soil Mechanics, 2010, 31(1): 246-252.

[2] 谭成轩, 张鹏, 郑汉淮, 等. 雅砻江锦屏一级水电站坝址区实测地应力与重大工程地质问题分析[J]. 地质工程学报, 2008, 16(2): 162-163.

TAN Chengxuan, ZHANG Peng, ZHEN Hanhuai, et al. An analysis on in-situ initial stress measurements and major engineering geology issues at the dam site area of JINPING first stage hydropower station[J]. Journal of Engineering Geology, 2008, 16(2): 162-163.

[3] 周济芳, 曾雄辉, 周春宏, 等. 锦屏二级水电站引水隧洞TBM 施工工法研究[J]. 岩石力学与工程学报, 2011, 30(1): 149-154.

ZHOU Jifang, ZENG Xionghui, ZHOU Chunhong, et al. Study of TBM construction of diversion tunnel for Jinping II hydropower station[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(1): 149-154.

[4] 谭青, 朱逸, 夏毅敏, 等. 节理特征对TBM 盘形滚刀破岩特性的影响[J]. 中南大学学报(自然科学版), 2013, 44(10): 4040-4046.

TAN Qing, ZHU Yi, XIA Yimin, et al. Influence of joint characteristics on rock fragmentation induced by TBM disc cutter[J]. Journal of Central South University (Science and Technology), 2013, 44(10): 4040-4046.

[5] 谭青, 徐孜军, 夏毅敏, 等. 2 种切削顺序下TBM 刀具破岩机理的数值研究[J]. 中南大学学报(自然科学版), 2012, 43(3): 940-946.

TAN Qing, XU Zijun, XIA Yimin, et al. Numerical study on mode of breaking rock by TBM cutter in two cutting orders[J]. Journal of Central South University (Science and Technology), 2012, 43(3): 940-946.

[6] HAIMSON B C, CHANG C. True triaxial strength of KTB amphibolites under borehole wall conditions and its use to estimate the maximum horizontal in-situ stress[J]. Journal of Geophysical Research, 2002, 107(B10): 2257-2271.

[7] 刘泉声, 胡云华, 刘滨. 基于试验的花岗岩渐进破坏本构模型研究[J]. 岩土力学, 2009, 30(2): 289-296.

LIU Quansheng, HU Yunhua, LIU Bin. Progressive damage constitutive models of granite based on experimental results[J]. Rock and Soil Mechanics, 2009, 30(2): 289-296.

[8] GERTSCH R, GERTSCH L, ROSTAMI J. Disc cutting tests in Colorado red granite: implications for TBM performance prediction[J]. International Journal of Rock Mechanics & Mining Sciences, 2007, 44(2): 238-246.

[9] ACAROGLU O. A fuzzy logic model to predict specific energy requirement[J]. Tunnel and Underground Space Technology, 2008, 10(6): 10-16.

[10] CIGLA M, OZDEMIR L. Computer modeling for improved production of mechanical excavators[C]//Proceedings of the Annual Meeting of the Society for Mining. Salt Lake City: Metallurgy and Exploration (SME), 2000: 1-12.

[11] CHANG S H, CHOI S W, BAE G J. Performance prediction of TBM disc cutting on granitic rock by the linear cutting test[J]. Tunneling and Underground Space Technology, 2006, 21(3): 271-279.

[12] 张照煌, 叶定海, 袁昕. 岩石在盘形滚刀作用下的性能研究[J]. 水力学报, 2011, 42(10): 1247-1251.

ZHANG Zhaohuang, YE Dinghai, YUAN Xin. Study on rock mechanical properties under the effect of disc cutter head[J]. Shuili Xue Bao, 2011, 42(10): 1247-1251.

[13] 龚秋明, 佘祺锐, 侯哲生, 等. 高地应力作用下大理岩岩体的TBM掘进试验研究[J]. 岩土力学和工程学报, 2010, 29(12): 2522-2532.

GONG Qiuming, SHE Qirui, HOU Zhesheng, et al. Experimental study of marble TBM penetration in marble rock mass under high geostress[J]. Chinese Journal of Geotechnical Engineering, 2010, 29(12): 2522-2532.

[14] WITTKE W. Rock mechanics: theory and applications with case histories[M]. Berlin: Springer Verlag, 1990: 1-1075.

[15] XIA Yimin, OUYANG Tao, ZHANG Xinming, et al. Mechanical model of breaking rock and force characteristic of disc cutter[J]. Journal of Central South University, 2012, 19(7): 1846-1852.

[16] 周春宏, 曹强, 廖卓, 等. 锦屏辅助洞竣工报告: 工程地质篇[R]. 杭州: 中国水电工程顾问集团华东勘察设计研究院, 2009: 58.

ZHOU Chunhong, CAO Qiang, LIAO Zhuo, et al. Completion report of assistant tunnel of Jinping hydropower station: engineering geology[R]. Hangzhou: Hydro China Huadong Engineering Corporation, 2009: 58.

(编辑  陈爱华)

收稿日期：2015-02-13；修回日期：2015-04-20

基金项目(Foundation item)：国家重点基础研究发展计划(“973”计划)项目(2013CB035401)；国家高技术研究发展计划(“863”计划)项目(2012AA041801)；国家自然科学基金资助项目(51274252)；湖南省科技计划项目(2013GK3003) (Project (2013CB035401) supported by the National Basic Research Program of China; Project (2012AA041801) supported by the National High Technology Research and Development Program of China; Project (51274252) supported by the National Natural Science Foundation of China; Project (2013GK3003) supported by the Technology Support Plan of Hunan Province)

通信作者：夏毅敏，博士，教授，博士生导师，从事大型掘进装备设计方面研究；E-mail：xiaymj@ csu.edu.cn