J. Cent. South Univ. Technol. (2008) 15(s1): 005-008

DOI: 10.1007/s11771-008-302-6

On energy boundary layer equations in power law non-Newtonian fluids

ZHENG Lian-cun(郑连存)¹, ZHANG Xin-xin(张欣欣)²

(1. Department of Mathematics and Mechanics, University of Science and Technology Beijing,

Beijing 100083, China;

2. Mechanical Engineering School, University of Science and Technology Beijing,

Beijing 100083, China)

Abstract: The hear transfer mechanism and the constitutive models for energy boundary layer in power law fluids were investigated. Two energy transfer constitutive equations models were proposed based on the assumption of similarity of velocity field momentum diffusion and temperature field heat transfer. The governing systems of partial different equations were transformed into ordinary differential equations respectively by using the similarity transformation group. One model was assumed that Prandtl number is a constant, and the other model was assumed that viscosity diffusion is analogous to thermal diffusion. The solutions were presented analytically and numerically by using the Runge-Kutta formulas and shooting technique and the associated transfer characteristics were discussed.

Key words: power law fluids; heat transfer; similarity solution; nonlinear boundary value problem

1 Introduction

Recently, considerable attention has been devoted to the problem of how to predict the drag force behavior of non-Newtonian fluids. The main reason for this is probably that fluids(such as molten plastics, pulps, slurries, emulsions), which do not obey the Newtonian postulate that the stress tensor is directly proportional to the deformation tensor, are produced industrially in increasing quantities, and are therefore in some cases just as likely to be pumped in a plant as the more common Newtonian fluids. Understanding the nature of this force by mathematical modeling with a view to predicting the drag forces and the associated behavior of fluid flow has been the focus of considerable research work. In addition, the mathematical model considered in this paper has significance in studying many problems of engineering^[1-3].

2 Boundary layer governing equations

SCHOWALTER^[2] applied the boundary layer theory to power law pseudo-plastic fluids and developed the two-dimensional and three dimensional boundary layer equations for the momentum transfer. ACRIVOS  et al^[3] considered the momentum and heat transfer for a non-Newtonian fluids past arbitrary external surfaces. In power law non-Newtonian fluids, the kinematic viscosity

is characterized as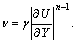The case n=1 corre-

sponds to a Newtonian fluid, the case 0＜n＜1 is “power law” relation proposed as being descriptive of pseudo-plastic non-Newtonian fluids and the case n＞1 describes the dilatant fluid^[4-5].

The similarity equation for momentum boundary layer of power law fluids as

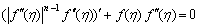             (1)

              (2)

Eqn.(1) has been used to describe the momentum boundary layer transfer in power law non-Newtonian fluids for more than 40 years^[6-8]. However, the similarity equation for energy boundary layer has not been established up to now.

In this paper, the characteristics of heat transfer in power law non-Newtonian fluids were investigated. A special emphasis is given to the formulation of boundary layer equations, which provides similarity solutions.

In order to set up the equation for the energy balance in a flow, we consider a fluid particle of mass dM=ρdV and volume dV=dxdydz in a Cartesian coordinate system and follow it on its path in the flow. According to the first law of thermodynamics, the gain in total energy DE_t (the index t stands for total energy) in unit time Dt is equal to the heat supplied to the mass element 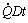 and the work done on the element  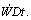Therefore

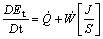                            (3)

where  DE_t/Dt is the substantial change in E_t,  is the heat flux, and this generally has both a local part and a convective part. Heat can be supplied both by heat conduction and by heat radiation. For small temperature differences, however, the radiation is generally not considerable, and will thus not be taken into account in this paper. The heat transferred per unit surface area and per unit time is denoted by the heat flux vector q(q_x, q_y, q_z) ([q]=J/(m²?s)). Therefore the heat entering the volume element through the surface element perpendicular to the x direction per unit time is q_xdydz, while that exiting per unit time is [q_x+(?q_x/?x)dx]dydz. Therefore the supply of heat in the  direction in time Dt is 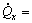-(?q_x/?x)? dxdydz=-(?q_x/?x)dx. Thus the total supply of heat is

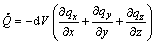                    (4)

Hence the supply of heat is proportional to the divergence of the heat flux vector q. Since the divergence is a measure for the source strength of the vector field in question, the term  is strictly speaking also a source term. The total energy E_t generally consists of three parts: the internal energy dM?e, the kinetic energy (1/2)dM?v² and the potential energy dM?Ψ. One more transport equation which connects the heat flux vector q with the temperature field must be connected the balance equation for the energy. From Fourier’s law, we have for heat conduction:

q=-λgradT                                  (5)

where  the thermal conductivity λ is a positive physical property. Therefore the energy equation finally is

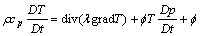             (6)

with the dissipation function  .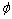

Case 1  Assume that the Prandtl number is a constant, in terms of the relationship of Prandtl number N_pr to the thermal diffusivity α, the thermal diffusivity is defined as a function of ν for U≠0 such that N_pr=γ/ω with γ and ω as positive constant and a=a₀ for U=0.

Case 2  Assume that the viscosity diffusion is analogous to thermal diffusion, in terms of the analogy, the thermal diffusivity is defined as a function of f(gradT)  and a=a₀ for ?T/?Y=0

The stream function ψ(x, y), similarity variable η and dimensionless temperature function w(η) are defined as^[9]:

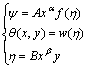                             (7)

where  A, B, α and β are constants to be determined, and f(η) denotes the dimensionless stream function. Choosing β=-α, AB=1, in terms of u=?ψ/?y, v=-?ψ/?x, substituting u and v by combining with α=1/(n+1), B=(n+1)^-1/(n+1). Then we obtain cases 1 and 2 respectively

Case 1

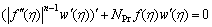          (8a)

Case 2

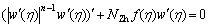           (8b)

the boundary conditions are

                        (9)

Eqns.(8a) or (8b) with boundary conditions (9) are the similarity equations in power law fluids. The analytical solutions are respectively:

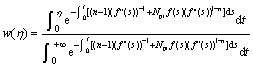
Or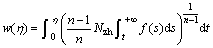

The equations can be solved by utilizing the solutions of momentum Eqns.(1) and (2) by using the Runge-Kutta formulas and shooting technique.

3.1 Solutions of Eqns.(8a) and (9)

Figs.1 and 2 show the dimensionless temperature profiles for different power law index n and the generalized Prandtl number N_pr.

The solutions indicate that the length scale of thermal diffusion is significantly different for the values of power law index and Prandtl number. The thermal diffusion ratio increases with the increase of n (0＜n≤1) and N_pr (0＜N_pr≤10). For N_pr＞1, the length scale of thermal diffusion can be significantly less than that of viscous diffusion, and this phenomenon is more obvious as N_pr increases.

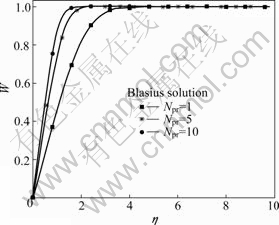
Fig.1 Dimensionless temperature profiles (case 1 for n=1.0, N_Pr=1 to 10)

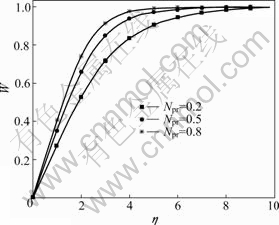
Fig.2 Dimensionless temperature profiles (case 1 for n=0.8, N_Pr=0.2 to 0.8)

The temperature boundary layer is much thinner over a given surface than the momentum boundary layer for large Prandtl numbers. If we denoted the thickness of temperature boundary layer by δ_T and the thickness of momentum boundary layer by δ, we have δ_T＜δ.

3.2 Solutions of Eqns.(8b) and (9)

Figs.3 and 4 show the temperature profiles for various values of parameters n and N_Zh.

It is seen that the length scale of thermal diffusion is significantly different for the values of n and N_Zh. The thermal diffusion ratio increases with the increase of n  (0＜n≤1) and N_Zh (0＜N_Zh≤1). The temperature boundary layer is thinner over a given surface than the momentum boundary layer for larger N_Zh. From Fig.4, it can be seen that the temperature is a decreasing function of n (0＜n≤1). Physical meaning of which is that the rates of thermal diffusion decreases with an increase in the power law index n.

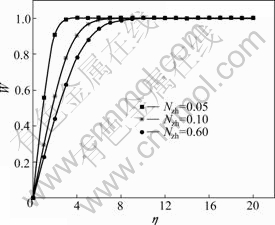
Fig.3 Dimensionless temperature profiles (case 2 for n=0.3, N_Zh=0.05 to 0.60)

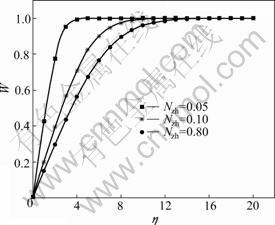
Fig.4 Dimensionless temperature profiles (case 2 for n=1.0, N_Zh=0.05 to 0.8)

For generalized thermal diffusivity a is constant, both cases 1 and 2 reduce to the Acrivos-Shah heatboundary layer model in power law fluids. And for n=1, all the results are qualitatively agree very well with that of the Blasius problem in Newtonian fluids which have been discussed by many authors^[1].

4 Conclusions

A theoretical analysis for hear transfer mechanism and the constitutive equation models for laminar boundary layer transport in power law non-Newtonian fluids are presented. Two energy transfer constitutive equations models are proposed based on the assumption of similarity of velocity field momentum diffusion and temperature field heat transfer. The similarity solutions are presented analytical and numerically by using the Runge-Kutta formulas and shooting technique and the associated transfer characteristics are discussed in detail.

[1] SCHLICHTING H. Boundary layer theory [M]. New York: McGraw-Hill, 1979.

[2] SCHOWALTER W R., The Application of boundary-layer theory to power-law pseudoplastic fluids: Similar solutions [J]. AIChE Journal, 1960, 6: 24-28.

[3] ACRIVOS A, SHAH M J, PETERSEN E E. Momentum and heat transfer in laminar boundary-layer flows of non-Newtonian fluids past external surfaces [J]. AIChE Journal, 1960, 6: 312-317.

[4] HADY F M. Mixed convection boundary-layer flow of non- Newtonian fluids on a horizontal plate [J]. Applied Mathematics and Computation, 1995, 68: 105-112.

[5] HOWELL T G., JENG D R, DE WITT K J. Momentum and heat transfer on a continuous moving surface in power law fluid [J]. Int J Heat Mass Transfer, 1997, 40: 1853-1861.

[6] CHEN Chien-Hisn. Effect of viscous dissipation on heat transfer in non-Newtonian liquid film over an unsteady stretching sheet [J]. Journal of Non-Newtonian Fluid Mechanics, 2005, 135: 128-135.

[7] WANG C, POP I. Analysis of the flow of a power law fluid film on an unsteady stretching surface by means of homotopy analysis method [J]. Journal of Non-Newtonian Fluid Mechanics, 2006, 138: 161-172.

[8] ZHENG Lian-cun, ZHANG Xin-xin, HE Ji-cheng. Existence and estimate of positive solutions to a nonlinear singular boundary value problem in the theory of dilatant non-Newtonian fluids [J]. Math Comp Model, 2007, 45: 387-393.

[9] ZHENG Lian-cun, ZHANG Xin-xin, LU Chun-qing. Heat transfer of power law non-Newtonian [J]. Chin Phys Lett, 2006, 23(12): 3301-3304.

(Edited by YANG You-ping)

Foundation item: Project(50476083) supported by the National Natural Science Foundation of China

Received date: 2008-06-25; Accepted date: 2008-08-05

Corresponding author: ZHENG Lian-cun, Professor; Tel: +86-10-62332002; E-mail: liancunzheng@163.com