文章编号：1004-0609(2010)05-0969-07

准晶与其近似相模拟中的势函数

孔祥春，胡望宇，邓辉球

(湖南大学 物理与微电子科学学院，长沙 410082)

摘  要：原子间相互作用势函数是从原子尺度上对材料各种特性进行计算机模拟研究的基础。由于准晶及其近似相特殊的几何构型，其采用的相互作用势的主要特点是包含传统势函数中没有的振荡项。准晶体系势函数大体分为两类：一类是以Dzugutov势和LJG势为代表的基于传统势函数的作用势。这两种势常用于单原子体系与双原子体系的准晶体系模拟，Dzugutov势是一种短程相互作用，它倾向于形成聚四面体，常用于玻璃态的体系中。LJG势加强了长程相互作用，是简单准晶体系模拟中应用最广泛的相互作用势。另一类是以Moriarty-Widom势与Force Match方法势为代表的Realistic型势函数，这种势函数基于第一性原理计算或实验结果，在多元合金准晶体系模拟中有广泛的应用。主要介绍以上两类势函数，并对其特点进行评述。

关键词：原子间相互作用势；准晶；势函数；准晶势函数；Realistic型势函数；计算机模拟

中图分类号：O 469　　                  文献标志码：A

Interatomic potentials for simulation of

quasicrystal and its approximant

KONG Xiang-chun, HU Wang-yu, DENG Hui-qiu

(College of Physics and Micro-electronic Science, Hunan University, Changsha 410082, China)

Abstract: Interaction potentials are essential in the atomic-scale computer simulation for materials properties. In contrast to the regular potentials, the potential functions for quasicrystal and its approximant have many local minimums due to its particular topology. There are mainly two kinds of potentials for quasicrystal. One is the potentials based on regular ones represented by Dzugutov potential and LJG potential. They are generally applied in the simulation of monatomic and diatomic systems. Dzugutov potential is a short-term interaction which strongly favors polytetrahedral clusters, and it is frequently applied in the simulation of glasses. LJG potential strengthens the long-range interaction compared to Dzugutov potential. It is the most widely used interaction in the simulation of simple systems. The other kind is Realistic potentials represented by Moriarty-Widom potential and potentials from Force Match method. These potentials are based on the first principle and experimental results, which plays an important role in the simulation of alloy systems such as AlNiCo. Those potentials are reviewed and some remarks are given.

Key words: interatomic potential; quasicrystal; potential function; quasicrystal potential function; Realistic potential function; computer simulation

随着计算机软硬件的快速发展，计算机模拟在现代材料学、物理学和化学等学科研究当中起到越来越重要的作用，逐渐成为与理论研究和实验研究几乎同等重要的研究手段。计算机模拟一方面能从微观尺度上很好地解释某些已有实验结果，另一方面又能根据已有知识来预测某些材料的物理、化学和力学性能等。计算机模拟中最常用的是分子动力学方法和蒙特卡洛方法。在基于原子尺度上的计算机模拟过程中，最关键的是选择合适的原子间相互作用势函数。通常使用的原子间相互作用势主要有两体势(例如Lennard- Jones势^[1])、三体势(例如Tersoff势^[2])和多体势(例如Embedded Atom Method，EAM势^[3-4])。两体势一般由吸引项和排斥项两部分组成，它仅考虑两个原子间的相互作用，而忽略了原子间的多体作用效应。这类势比较适用于密堆结构和原子间或团簇间电荷重叠较少的情形^[5]。三体势中通过加入与键夹角有关的项来考虑三体相互作用，成功地描述了C、Si、Ge等元素或其组成的共价化合物的特性。以EAM势为代表的多体势，能较好地描述绝大部分金属元素及其合金的各种性质^[6]。对于计算机模拟中这些常用势函数的特点及其在晶体和非晶材料中的应用情况，文献[5, 7-10]中已有不少很好的综述。但是在晶体和非晶之外的准晶及其近似相材料，由于其特殊的原子几何排列特征和电子性质，通常应用的势函数在处理准晶材料时都会遇到一定的困难。

适用于准晶体系的势函数与描述传统晶态和非晶态体系的势函数具有不同的特点，近几年来得到很大的发展。在此，本文作者分类列举近年来在准晶及其近似相模拟过程中常用到的几种原子间相互作用势函数，并对其函数特点和典型应用情况进行评述。

1  准晶模拟势函数的要求和特点

从结构上看，传统晶体包含平移对称性和旋转对称性，体系原子配位环境相对简单，从能量上表现为稳定的低能态。而复杂的准晶合金当中只包含旋转对称性而没有平移对称性，结构中包含传统晶体当中不存在的五重对称结构，因此，需要借助多于一种的基本结构来铺满整个空间，表现为某个或多个方向上出现准周期性排列以及富含五重对称的二十面体团簇子结构，为能量较高的亚稳结构。由于准晶与传统晶体在结构和能量等方面存在较大的差异，因此，在准晶模拟过程中采用的势函数有明显的特点。众所周知，在传统单势阱的金属原子间对势函数中仅考虑核子间相互作用。加入电子对核子的贡献后，金属原子间对势作用曲线就变成两部分^[11]：由一个强排斥中心加一组逐渐衰减的Friedel项构成，由此可以引入一类针对准晶体系的势函数。它的特点是中长程作用不是单调变化而是存在多个振荡项，振荡项会在势曲线中产生能量极值点，在结构上表现为出现多个亚稳的原子位置，亚稳位置两侧的势垒在一定条件下可以有效地束缚原子，从而保持准晶及其近似相体系的特殊几何结构。另外，振荡的势函数曲线也包含明确的物理意义，即在高维空间^[12]当中，平行空间(即实空间)的空间变化对应于声子，垂直空间的空间变化对应于相位子。相位子在物理空间的体现为准晶中某些原子从原来的亚稳位置翻过势垒跳跃到其近邻的另一亚稳位置^[13]，在准晶结构中表现为拼块邻近顶点的原子间跳跃。

2  准晶结构计算中的常用势函数

2.1  基于简单对势的势函数

2.1.1  Dzugutov对势

Dzugutov对势^[14]是单原子体系中常用的一种势, 它的提出是为了解决由液态或高温金属玻璃为初始态的体系逐渐退火过程当中结构原子局域结构的问题，其表达式如式(1)所示。Dzugutov对势曲线的显著特点是传统的Lennard-Jones势前半部分相同，而在势能最小值与截断距离之间加入一个有限高的势垒。

Φ(r)=Φ₁+Φ₂                                 (1)

其中：

≥

＜

  Φ₁=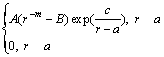

≥

＜

  Φ₂=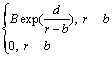

式中：r是原子间距离；a和c分别是第1条势曲线的截尾距离与稳定位置；b和d是第2条曲线中a与c对应的参数；A，B和m为调整参数。表1列出一组模型的势参数。

表1  Dzugutov对势对应的参数^[14]

Table 1  Parameters of Dzugutov pair potential^[14]

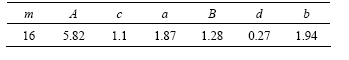
图1所示为表1对应的Dzugutov对势的势能曲线图。从图1可知：整个势能包含2个势能极小值和1个极大值，由1个强排斥中心加1个Friedel项构成。

与传统的势函数易形成密排结构的特性不同，Dzugutov势更趋向于形成聚四面体团簇。提出Dzugutov势的出发点是在玻璃态中的应用，且它在这

图1  Dzugutov对势曲线^[14]

Fig.1  Curves of Dzugutov pair potential^[14]

种体系当中的应用取得了比较好的结果。如液态金属或金属玻璃在退火冷却过程中当冷却速度足够慢时可以形成稳定的十二次准晶结构^[15]。关于结构振荡性质的研究可以证明，δ相晶体是二十面体金属玻璃体系的对应晶体相^[16-17]。MATTILA等^[18]采用Dzugutov势和EAM势对高能粒子引发的辐照损伤对Ni、P单质及NiP玻璃态结构随时间的影响进行了模拟，发现包含二十面体序的结构在平衡状态下有很强的固定能力^[19]。另外，使用Dzugutov势发现拓扑结构的不同会导致不同的振动激发方式，并与其驰豫稳定的金属相振动方式近似^[20]。

2.1.2  Lennard-Jones-Guass势(LJG)

由于Dzugutov势是一种针对性的相互作用势，经常应用于简单的单成分金属玻璃体系，相对包含电子能量考虑的对势相互作用，该势函数仅截断在第一个Friedel项的极小值处，而将其他中长程项忽略，因而，中长程作用表征能力不强。一种有效方法是在势曲线中延长Friedel项的截断位置，LJG势^[21]就是其中的一种，其势函数的形式如下：

    (2)

LJG势包含6个参数，式(2)中前两项形成一个位于r=d处深度ε的Lennard-Jones曲线，而后加入一个高斯项，ε₀用于调整第二势能最低值处的势阱深度，这个阱势位于r=r₀处，宽度为d。图2所示为一组对应不同r₀的LJG势曲线。

LJG势的原理是在传统Lennard-Jones势的基础上在势能最小值位置与截断距离之间加入一个高斯分布，与Dzugutov势相比，LJG的意义相当于在前两个Friedel振荡项之间进行截断，从而得到一个具有包含双势阱和单势垒的作用函数，这样的结果是直接引入一个稳定位置和一个亚稳定位置。根据极值的位置与势阱深度的不同，可以得到不同基态的LJG函数。

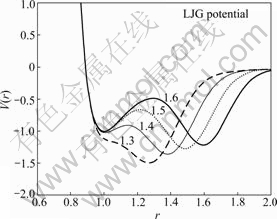
图2  不同r₀时LJG势曲线^[22]

Fig.2  LJG potential for different r₀^[22]

ROTH等^[22]使用LJG势研究了二维、三维结构下Penrose拼块不同子结构格点的稳定性，发现格点处不同的子团簇堆砌体系稳定性由子团簇本身的性质决定。ENGEL和TREBIN^[23]采用二维单原子准晶体系，证明十次准晶是不由匹配规则控制的理想随机拼块结构，在临界温度附近出现的准晶与其近似相可逆转变是由大量拼块内原子跳跃实现的。

LJG势最大的优点在于，它研究简单准晶体系的结构和热力学性质可以得到很好的结果，而且它能够在模拟过程当中直接观察到准晶结构与其晶体近似相之间的相互转化。图3所示为由MC方法研究单原子二元体系中加热与退火过程中十次对称拼块D与相位子应变χ₁和χ₂的变化规律，可以得到D拼块(D tiles)变化过程是完全可逆的。其中：Dec和X_i分别表示十次准晶与其对应的近似晶体相；T_m表示体系的熔点。当T＞0.4T_m时，整个体系当中χ₁和χ₂全部降为0，表明体系变为十次准晶，体系发生相变，在退火过程中整个过程可逆。

与Lennard-Jones势不同，调节Friedel项位置势阱的位置和深度，对体系所得的基态结构类型产生明显的影响。从图4可以得到在同一单原子体系中r₀和深度(ε)的变化；由于势能曲线存在双势阱，因此，含有2个势能极小值点，相当于体系当中出现两套晶格常数的共同作用，从而形成不同基态结构。

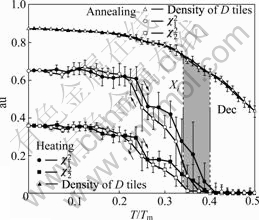
图3  十次随机拼块准晶与其近似相的相变^[22]

Fig.3  Phase transition between decagonal RT and approximant χ_i^[22]

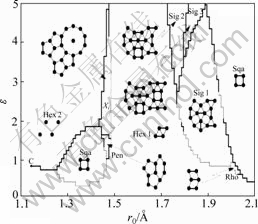
图4  T=0, δ²=0.02时LJG势结构相图^[22]

Fig.4  Phase diagram of LJG potential at T=0 and δ²=0.02^[22]

ENGEL和TREBIN^[23]从单原子体系中发现由液态体系得到的多种晶体，以及十次准晶和十二次准晶是可以通过原子自组装得到的。在退火过程中，熵稳定的十次准晶通过相位子跳跃实现结构重排向近似相发生可逆的相变，整个体系的变化过程表现为不同晶格常数之间的竞争。LJG势对非晶结构同样具有很好的描述能力，HOANG和ODAGAKI ^[25]从单原子体系液体冷却得到的无序结构出发，研究了纳米颗粒的结构性质，并发现大量的二十面体短程序。

2.1.3 小结

Dzugutov倾向于形成聚四面体结构，这种结构比传统对势作用能够更有效地保持亚稳定高能结构，这种结构特征对于准晶性质非常重要。利用LJG势在二维体系的单类原子结构中能够模拟出准晶体与晶体相的可逆性相变。Dzugutov势主要用于描述短程相互作用，而用于描述长程作用时有明显缺陷，因此，无法得到纯粹的液态或气态结构体系。LJG势中第二势阱的位置及其深度对最终结构的影响也应当特别注意。另外，虽然两种势都取得了很好的结果，但是它们仍然是一种经验性势函数，研究对象相对简单，在解决多元准晶与近似相问题上仍然存在较大不足。

2.2  Realistic型势函数

2.2.1  Moriarty-Widom有效对势

为了解决多元体系中准晶结构问题，发展了精度更高的Realistic型势函数(Realistic potentials)。这种势以第一性原理或实验结果为基础，较之前的势函数准确度有了很大提高。

MORIARTY和WIDOM等^[26-27]从密度泛函理论出发，将第一性原理中的DFT计算进行级数展开，并采用相关的物理近似，给出复杂合金体系中Al与过渡金属相互作用的有效对势作用。图5所示为三元准晶体系AlNiCo中的Moriarty-Widom有效对势，从对势曲线可以看出，每种对势作用都包含明显的振荡行为，这与理论中的Friedel振荡一致，同时大量亚稳定位置的存在能够有效地维持体系结构的相对稳态。

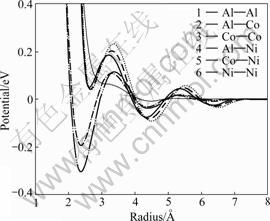
图5  AlNiCo体系中Moriarty-Widom有效对势^[26]

Fig.5  Moriarty-Widom effective pair potentials for decagonal AlNiCo^[26]

MIHALKOVI?等^[28]以随机拼块的36?和72?这2种菱形结构为基础，利用实验得到的准晶体系的性质与Moriarty-Widom有效对势，通过Monte Carlo模拟发现，在系统能量最低的条件下可以得到拼块描述的最小限制(Minimally constrained)与高限制(Highly constrained simulation)2种条件的准晶结构。结果发现，得到的体系结构与实验得到的结构相比仅仅是完整的十边形的表观密度偏低，这可能是由于真实结构中的相位子堆垛无序导致十边形的表观密度上升^[29]。BOISSIEU等^[30]利用该对势很好地重现了从实验中得到的Zn-Mg-Sc准晶体系与其Zn-Sc晶体相的横向色散关系与结构因子特征，它在Al-Ni-Co体系的性质与结构计算上也得到了重要的结果^[31-33]。

HOCKER和G?HLER^[34]使用Moriarty-Widom对势研究了AlNiCo与AlCuCo相关体系中Al原子扩散行为，发现体系中同种元素在不同原子环境下活动性差异明显，在T＞0.6 T_m时发生强烈的Al原子扩散现象。图6给出了4种十次准晶结构中Al原子扩散的Arrhenius关系。其中：x为准周期性方向；z为周期性扩散方向。从图6可知在4种结构中Al在周期性方向的扩散速度明显比准周期方向的快，而且具有比周期性方向更大的扩散激活能，表示Al原子更容易在周期性方向发生扩散。

图6  AlCuCo体系中Al原子扩散的Arrhenius关系^[31]

Fig.6  Arrhenius plots for Al diffusion in AlCuCo^[31]

2.2.2  力匹配方法势

为了解决一般性的体系相互作用， ERCOLESSI和ADAMS^[35]提出了“力匹配方法(Force-match method)”，它是通过给定体系需要考虑的参考结构，选取模型势的类型，利用第一性原理得到关于力、应力和能量等方面相对准确的数据，然后，利用优化的方法使由模型势得到的对应量不断逼近第一性原理值，使势函数精度得到提高。势参数通过“力匹配方法”由式(3)获得。

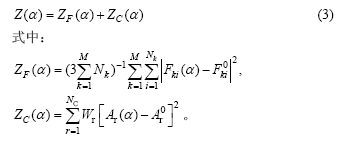
随着Z值收敛计算值逐渐逼近得到第一性原理值的近似值，并由此得到势参数列α的优化值。

当前使用“力匹配方法”得到的复杂合金相中的原子间相互作用势已经得到了很好的验证，通过对二维准周期的AlNiCo层状结构连续加温的方法得到与Moriarty-Widom对势结果吻合的体系热稳定性，在0.5T_m下体系结构无明显变化，相位子跃迁机率很小，原子运动方向仅仅集中在周期方向的原子面之内，并得到了与实验结果相近的熔点。通过这种势计算了AlNiCo体系高温下的Al原子扩散，得到了很好的结果^[36]。另外，它在包含二十面体结构的二十面体准晶结构中也得到了很好的应用，在研究二十面体CaCd准晶结构的1/1准晶近似相CaCd₆构的无序化转变  过程中，得到与实验值非常接近的无序化转变温    度^[37-39]。除了上述结果，力匹配方法还在NbCr₂中的裂纹扩展^[40]与Zn₂Mg的动力学结构因数^[41]的计算上取得了好的结果。

2.2.3 小结

Moriarty-Widom对势采用级数展开方法得到了包含类Friedel项的多级振荡两体间相互作用。与Moriarty-Widom对势固定的表达形式不同，力匹配方法得到的势的表达形式比较灵活，势函数形式主要取决于选取的模型势函数，通过第一性原理值对参考值进行迭代修正。这两种势都是基于第一性原理值，能够有效模拟多元准晶与其近似相的结构和性质。由于力匹配方法形式灵活，可以应用EAM等势模型，使用方便，其主要优点在于结合了传统势的计算能力和第一性原理的准确性，使得相互作用势的精度有了很大提高。但势的作用范围局限于势调节过程中的几种特殊结构，而且势拟合过程当中的过多变量使势函数调节比较困难。

3  总结与展望

1) 对准晶结构的势函数特点及常用势函数进行了较为系统的总结，发现对势项中加入电子对核子作用后，准晶结构中原子间长程作用可能并不是单调变化的而是存在多个振荡项，它能有效维持准晶特殊的几何结构特征，同时振荡项在势曲线中产生若干个能量极值点，与准晶体系的较高能量相对应，因此，描述准晶结构时采用的势函数曲线与描述晶态和非晶态时有所不同。

2) 随着现代计算机软硬件的发展，精度较高的第一性原理计算能够处理越来越大的原子体系和计算越来越多的材料性质，但是对于大而复杂的准晶体系仍然无法处理。通过与第一性原理计算和实验测量结果相结合，拟合得到有关经验势函数参数，是一种对准晶结构和性质进行原子尺度模拟的有效方法。

REFERENCES

[1] LENNARD-JONES J E. On the determination of molecular fields [J]. Proc Roy Soc A, 1924, 106: 463-469.

[2] TERSOFF J. New empirical model for the structural properties of silicon [J]. Phys Rev Lett, 1986, 56: 632-635.

[3] DAW M S, BASKES M I. Semiempirical, quantum mechanical calculation of hydrogen embrittlement in metals [J]. Phys Rev Lett, 1983, 50: 1285-1288.

[4] DAW M S, BASKES M I. Embedded atom method: Derivation and application to impurities, surface and other defects in metals [J]. Phys Rev B, 1984, 29: 6443-6453.

[5] 欧阳义芳, 钟夏平. 凝聚态物质计算和模拟中使用的相互作用势[J]. 力学进展, 2006, 36(3): 321-343.
OUYANG Yi-fang, ZHONG Xia-ping. Interatomic potentials of computer simulation of condensed matters [J]. Advances In Mechanics, 2006, 36(3): 321-343.

[6] 张邦维, 胡望宇, 舒小林. 嵌入原子方法理论及其在材料科学中的应用: 原子尺度材料设计理论[M]. 长沙: 湖南大学出版社, 2003.
ZHANG Bang-wei, HU Wang-yu, SHU Xiao-lin. Theory of embedded atom method and its application to materials sscience: Atomic scale materials design theory [M]. Changsha: Hunan University Press, 2003.

[7] 王月华, 刘艳侠, 王 逊. 金属及合金中的原子间相互作用势[J]. 辽宁大学学报, 2006, 33(1): 24-28.
WANG Yue-hua, LIU Yan-xia, WANG Xun. Interatomic potentials in metal and alloy [J]. Journal of Liaoning University, 2006, 33(1): 24-28.

[8] 陈 强, 曹红红, 黄海波. 分子动力学中势函数研究[J]. 天津理工学院学报, 2004, 20(2): 101-105.
CHEN Qiang, CAO Hong-hong, HUANG Hai-bo. A research on the interatomic potential in molecular dynamics (MD) [J]. Journal of Tianjin Institute of Technology, 2004, 20(2): 101-105.

[9] LI J H, DAI X D, LIANG S H, TAI K P, KONG Y, LIU B X. Interatomic potentials of the binary transition metal systems and some applications in materials physics [J]. Physics Reports, 2008, 455: 1-134.

[10] ERKOC S. Empirical many—Body potential energy functions used in computer simulations of condensed matter properties [J]. Phys Reports, 1997, 278: 79-105.

[11] HAFNER J. From Hamiltonians to phase diagrams [M]. Berlin: Springer-Verlag, 1987.

[12] DUNEAU M, KATZ A. Quasiperiodic patterns [J]. Phys Rev Lett, 1985, 54: 2688-2691.

[13] 田 鹤. 复杂结构合金相中特殊缺陷的显微结构研究[D]. 北京: 中国科学院物理研究所, 2006: 31.
TIAN He. TEM study of microstructures of defects in the structurally complex metallic alloy phases [D]. Beijing: Institute of High Physics, Chinese Academy of Sciences, 2006: 31.

[14] DZUGUTOV M. Glass formation in a simple monatomic liquid with icosahedral inherent local order [J]. Phys Rev A, 1992, 46: R2984-R2987.

[15] DZUGUTOV M, SIMDYANKIN S I, ZETTERLING F H. Decoupling of diffusion from structural relaxation and spatial heterogeneity in a supercooled simple liquid [J]. Phys Rev Lett, 2002, 89: 195701-4.

[16] SIMDYANKIN S I, TARASKIN S N, DZUGUTOV M, ELLIOTT S R. Vibrational properties of the one-component σ phase [J]. Phys Rev B, 2000, 62: 3223-3231.

[17] SIMDYANKIN S I, TARASKIN S N, ELENIUS M, ELLIOTT S R, DZUGUTOV M. Nature of vibrational eigen modes in topologically disordered solids [J]. Phys Rev B, 2002, 65: 104302-7.

[18] MATTILA T, NIEMINEN R M, DZUGUTOV M. Simulation of radiation-induced structural transformation in amorphous metals [J]. Phys Rev B, 1996, 53: 192-200.

[19] SADIGH B, DZUGUTOV M, ELLIOTT S R. Vacancy ordering and medium-range structure in a simple monatomic liquid [J]. Phy Rev B, 1999, 59: 1-4.

[20] SIMDYANKIN S I, DZUGUTOV M, TARASKIN S N, ELLIOTT S R. Connection between vibrational dynamics and topological order in simple glasses [J]. Phys Rev B, 2001, 63: 184301-5.

[21] STEIGERWALD M L, BRUS L E, ALIVISATOS A. Synthesis, stabilization, and electronic structure of quantum semiconductor nanoclusters [J]. Annu Rev Mater Sci, 1989, 19: 471-495.

[22] ROTH J, SCHILIING R, TREBIN H R. Stability of monatomic and diatomic quasicrystals and the influence of noise [J]. Phys Rev B, 1990, 41: 2735-2747.

[23] ENGEL M, TREBIN H R. Stability of the decagonal quasicrystal in the Lennard-Jones-Gauss system [J]. Phil Mag, 2008, 88: 1959-1965.

[24] ENGEL M, TREBIN H R. Self-assembly of monatomic complex crystals and quasicrystals with a double-well interaction potential [J]. Phys Rev Lett, 2007, 98: 225505-4.

[25] van HOANG V, ODAGAKI T. Molecular dynamics simulations of simple monatomic amorphous nanoparticles [J]. Phys Rev B, 2008, 77: 125434-11.

[26] MORIARTY J A, WIDOM M. First-principles interatomic potentials for transition-metal aluminides: Theory and trends across the 3d series [J]. Phys Rev B, 1997, 56: 7905-7917.

[27] WIDOM M, AL-LEHYANI I, MORIARTY J A. First-principles interatomic potentials for transition-metal aluminides (III). Extension to ternary phase diagrams [J]. Phys Rev B, 2000, 62: 3648-3657.

[28] MIHALKOVI? M, AL-LEHYANI I, COCKAYNE E, HENLEY C L, MOGHADAM N, MORIARTY J A, WANG Y, WIDOM M. Total-energy-based prediction of a quasicrystal structure [J]. Phys Rev B, 2002, 65: 104205-6.

[29] HENLEY C L, ELSER V, MIHALKOVI? M. Structure determinations for random-tiling quasicrystals [J]. Z Kristallogr, 2000, 215: 553-568.

[30] de BOISSIEU M, FRANCOUAL S, MIHALKOVI? M, et al. Lattice dynamics of the Zn-Mg-Sc icosahedral quasicrystal and its Zn-Sc periodic 1/1 appromant [J]. Nature Materials, 2007, 6: 977-984.

[31] JORAMATSU S, ISHII Y. Dynamic properties of Al-Ni-Co decagonal quasicrystals modeled by Ab initio interatomic pair potential [J]. J Phys Soc Jpan, 2007, 76: 034601-6.

[32] HIRAMATSU S, ISHII Y. Theoretical prediction of phase diagrams for Al-Co-Ni decagonal quasicrystals [J]. J Phys Soc Jpn, 2006, 75: 054602-6.

[33] GU N, HENLEY C L, MIHALKOVI? M. Co-rich decagonal Al-Co-Ni: Predicting structure, orientational order and puckering [J]. Phil Mag, 2006, 86: 593-599.

[34] HOCKER S, G?HLER F. Aluminium diffusion in decagonal quasicrystals [J]. Phys Rev Lett, 2004, 93: 075901-4.

[35] ERCOLESSI F, ADAMS J B. Interatomic potentials from first-principles calculations: The force-matching method [J]. Euro Phys Lett, 1994, 26: 583-588.

[36] HOCKER S, G?HLER F, BROMMER P. Molecular dynamics simulation of aluminium diffusion in decagonal quasicrystals [J]. Phil Mag, 2006, 86: 1051-1057.

[37] BROMMER P, G?HLER F, MIHALKOVI? M. Ordering and correlation of cluster orientations in CaCd6 [J]. Phil Mag, 2007, 87: 2671-2677.

[38] TAMURA R, EDAGAWA K, MURAO Y, TAKEUCHI S, SUZUKI K, ICHIHARA M, ISOBE M, UEDA Y. Order-disorder transition in cubic Cd₆Yb and Cd₆Ca [J]. J Non-cryst Solids, 2004, 334/335: 173-176.

[39] TAMURA R, NISHIMOTO K, TAKEUCHI S, EDAGAWA K, ISOBE M, UEDA Y. Universal low-temperature phase transition in Zn- and Cd-based crystalline approximants [J]. Phys Rev B, 2005, 71: 092203-4.

[40] R?SCH F, TREBIN H R, GUMBSCH P. Interatomic potentials and the simulation of fracture: C15NbCr2 [J]. Int J Fracture, 2006, 139: 517-526.

[41] BROMMER P, de BOISSIEU M, EUCHNER H, FRANCOUAL S, G?HLER F, JOHNSON M, PARLINSKI K, SCHMALZL K. Vibrational properties of MgZn₂ [J]. Z Kristallogr, 2009, 224: 97-100.

(编辑 杨 华)

基金项目：国家自然科学基金资助项目(50671035, 50871038)

收稿日期：2009-08-30；修订日期：2009-11-30

通信作者：胡望宇，教授，博士；电话：0731-88823971；E-mail: wangyuhu2001cn@yahoo.com.cn