J. Cent. South Univ. (2018) 25: 2537-2549

DOI: https://doi.org/10.1007/s11771-018-3934-1

Elasticity solution of laminated beams with temperature-dependent material properties under a combination of uniform thermo-load and mechanical loads

ZHANG Zhong(张忠)¹, ZHOU Wen-ling(周文领)², ZHOU Ding(周叮)¹, HUO Rui-li(霍瑞丽)¹, XU Xiu-li(徐秀丽)¹

1. College of Civil Engineering, Nanjing Tech University, Nanjing 211816, China;

2. Flood Control and Drought Relief Rescue Center of Jiangsu Province, Nanjing 211500, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: An exact solution for simply-supported laminated beams with material properties variable with temperature under a combination of uniform thermo-load and mechanical loads was investigated, based on the two-dimensional (2-D) thermo-elasticity theory. Firstly, the beam was divided into a series of layers with uniform material properties along the interfaces of the beam. The uniform thermo-load acted on each layer was transformed into a combination of the normal surface forces acted at the two ends and the transverse thermo-load. Secondly, the state space method was employed to obtain the general solutions of displacements and stresses in an arbitrary layer. Thirdly, based on the interfacial continuity conditions between adjacent layers, the relations of displacement and stress components between the top and bottom layers of the beam were recursively derived by use of the transfer-matrix method. The unknowns in the solutions can be solved by the mechanical loads acted on the top and bottom surfaces. The convergence of the present solutions was checked. The comparative study of the present solutions with the Timoshenko’s solutions and the finite element (FE) solutions was carried out. The effects of material properties variable with temperature on the thermo-elastic behavior of laminated beams were discussed in detail.

Key words: laminated beam; thermo-elasticity; analytical solution; transfer-matrix method; temperature-dependent material

Cite this article as: ZHANG Zhong, ZHOU Wen-ling, ZHOU Ding, HUO Rui-li, XU Xiu-li. Elasticity solution of laminated beams with temperature-dependent material properties under a combination of uniform thermo-load and mechanical loads [J]. Journal of Central South University, 2018, 25(10): 2537–2549. DOI: https://doi.org/10.1007/ s11771-018-3934-1.

1 Introduction

It is well known that composite structures are popular in modern engineering due to the advantages of good mechanical performance, low cost and convenient usage. During the past few decades, steel-concrete beams have been extensively applied to different engineering structures. Laminated glass structures [1, 2] and functionally graded material (FGM) structures [3-7] have attracted considerable attention. The laminated beams bearing mechanical loads could work under thermal environment. Generally, the main effects of temperature change on the laminated beam include the generation of thermal stresses due to difference in the material properties of every layer; and the variation of material properties due to softening of the beam [8-10]. The effects could affect the mechanical performance of the beam, reducing its service life. Therefore, it is significant for structural safety to study the effects of temperature on deformations and stresses in laminated beams.

A lot of theories for the analysis of beams and plates are available in literature [11-16]. The classical theories for beams and plates are, respectively, based on the Euler-Bernoulli hypothesis and the Kirchhoff hypothesis, which are commonly used due to the simplicity in engineering analysis. TIMOSHENKO [17] studied the bending problem of a two-layer strip under uniform thermo-load based on the Euler-Bernoulli beam theory. MOHANDES et al [18] studied the nonlinear free vibration and bending of micro/nano laminated composite Euler-Bernoulli beam under thermo-load. The classical theories are suitable for thin beams and plates but less accurate for thick beams and plates due to the neglect of the effects of transverse shear deformation. To improve the classical beam and plate theories, some refined theories have been proposed. First-order shear deformation theories were proposed by assuming the through-thickness distribution of transverse shear strain to be constant. Based on the first-order shear deformation theory, FU et al [19] studied the thermal buckling and postbuckling of symmetric laminated composite beams under uniform thermo-load considering geometric nonlinearity. MORADI et al [20] gave the buckling analysis of rectangular laminated plates under a uniform temperature distribution by use of the differential quadrature method. SHATERZADEH et al [21] presented the FE analysis of thermal buckling for rectangular laminated composite plates with circular cut-out. Based on an enhanced first-order shear deformation theory, HAN et al [22] presented the thermal stress analysis for laminated composite and sandwich plates. Higher-order shear deformation theories have been employed by many researchers, in which the displacement components are described by the power series expansion with respect to the thickness coordinate. According to the higher-order shear deformation theory, KHDEIR et al [23] carried out the thermal bending analysis of cross-ply rectangular plates. Najafizadeh et al [24] carried out the buckling analysis for functionally graded circular plates under several types of temperature fields and presented the closed-form solutions. SINGH et al [25] presented the buckling analysis of laminated composite plates under thermo-mechanical loads considering two transverse shear stress functions. Kapuria et al [26] made the analysis for laminated beams under thermal environment by presenting an efficient higher-order zigzag theory. Based on the trigonometric shear deformation theory, GHUGAL et al [27, 28] presented the displacement and stress fields of cross-ply laminated plates under uniformly distributed thermal-mechanical loads. Based on the hyperbolic shear deformation theory, SAYYAD et al [29] carried out the static analysis of orthotropic plates subjected to thermo-mechanical load. SAYYAD et al [30] developed a four-variable plate theory for the thermo-elastic bending analysis of laminated composite plates.

Elasticity theory has been used by researchers for analyzing beams and plates. Comparing with the results based on the classical theories, first-order theories, higher-order theories and some other refined theories, the results based on the elasticity theory are more accurate due to no any assumptions. Based on the thermo-elasticity theory, XU et al [31] developed analytical methods for beams with variable thickness under a combination of thermo-load and mechanical load. QIAN et al [32, 33] presented the thermo-elastic analysis for simply-supported laminated beams and arches. The temperature field was obtained using the Fourier’s law of thermal conduction. However, the temperature dependence of material properties was ignored and hence the analysis is not suitable for high temperature environment such as fire exposure. LV et al [34] presented the thermo-elasticity solution for functionally graded thick beams using differential quadrature method. The approximate laminate model was introduced to divide the beam into several layers with material properties in each layer assumed to be constant. PILIPCHUK et al [35] developed an analytical model for the cylindrical bending of sandwich plates with different temperature distributions at the plate outer surfaces. ALIBEIGLOO [36] presented the thermo- elasticity solution of sandwich circular plate with functionally graded core by employing differential quadrature method.

The literature review indicates that no research has been conducted on the analytical solution of laminated beams with temperature-dependent material properties based on the exact thermo- elasticity theory. In the present work, an analytical method is proposed to analyze the simply-supported laminated beams with material properties variable with temperature under a combination of uniform thermo-load and mechanical loads. The effects of material properties variable with temperature on the mechanical performance of the beam are discussed in detail.

2 Equivalent model of thermo-load

Firstly, we introduce an equivalent model that transforms the thermo-load into the mechanical load. Consider an isotropic 2-D body under a uniform temperature field with the increment △T from the stress-free state. The elastic modulus, Poisson ratio and thermal expansion coefficient of the body are E, μ and α, respectively. The body behavior is described by a rectangular coordinate system (x, y). The body is in the plane stress state, for which the thermo-elastic constitutive relations are

,

,

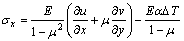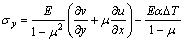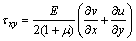                    (1)

where σ_x and σ_y are respectively the normal stresses in the direction of x and y axes; τ_xy is the shear stress; u and v are respectively the displacements in the direction of x and y axes.

Assuming that the body is free on all the surfaces, i.e.;

,

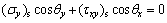                (2)

where θ_x and θ_y are respectively the angles between the external normal line and the x and y axes; The subscript s denotes the quantities located on the surface of the body.

Substituting Eq. (1) into Eq. (2) gives

,

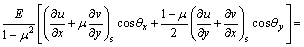
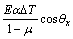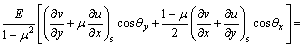
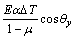                          (3)

The right sides of Eq. (3) can be respectively assumed as the surface forces in the direction of x and y axes. Thus, it is concluded that for an isotropic 2-D body, the displacements produced by the uniform thermo-load in the x and y directions are equivalent to those produced by the surface forces in the x and y directions, respectively.

3 Analytical model of laminated beam

A simply-supported beam with length L and total thickness H, made up of p perfectly bonded isotropic layers is shown in Figure 1(a). The thickness of layer i (i=1, 2, …, p) is h_i. The beam behavior is described by a global rectangular coordinate system (x, y). The beam is under mechanical loads q₁(x) and q₂(x) acted on the top and bottom surfaces, respectively. Meanwhile, the beam is under a uniform temperature field with the increment △T from the stress-free state, which is assumed at a constant temperature of T₀. Thus, the temperature field in the final state is T=T₀+△T. It should be mentioned that the thermal conductivity of each layer and the Fourier’s law are not required, since the temperature field is constant in the present analysis.

Now we focus on an arbitrary layer in the laminated beam. Without loss of generality, the layer i with a local rectangular coordinate system (x, y_i) is considered, as depicted in Figure 1(b). It is noted that the symbol i in the following equations denotes that the quantities correspond to layer i. The thermo-elastic constitutive relations of layer i are

,

,

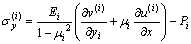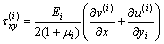                 (4)

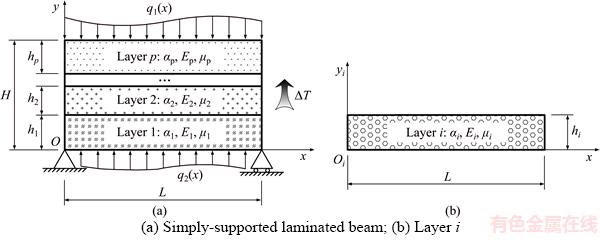
Figure 1 Analytical model:

where P_i=E_iα_i△T/(1–μ_i). The equilibrium equations with neglecting volume forces are

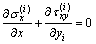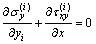,            (5)

The simply-supported end conditions are

,

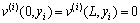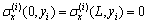(i=1, 2, …, p)       (6)

The top and bottom surface conditions of the beam are

,,,

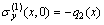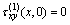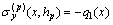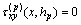                            (7)

The interfacial continuity conditions between adjacent layers are

, ,

, ,

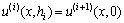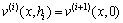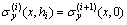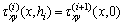(i=1, 2, …, p–1)                      (8)

According to the equivalent model developed above, the displacements of layer i produced by the uniform temperature increment △T can be equivalent to a combination of the following two parts: 1) in the x direction, the layer is subjected to normal surface forces acted at the two ends; 2) in the y direction, the layer is still under the thermo-load. In this case, the longitudinal stress σ(i) x of layer i can be written as

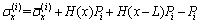            (9)

where the last item –P_i is the isotropic normal stress within layer i, as given in Eq. (4); 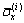is the longitudinal stress of layer i, which is free of surface forces at the two lateral ends; H(x)P_i+H(x–L)P_i are the normal surface forces acted at the two ends of layer i, which are expressed by employing the unit pulse functions H(x) and H(x–L) with the following definitions:

,

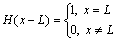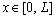,              (10)

Substituting Eq. (9) into the equilibrium Eq. (5) gives

,

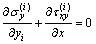                         (11)

where △(x) and △(x–L) are the Dirac delta functions, which are expressed in terms of the unit pulse functions by

,

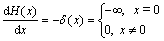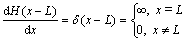             (12)

In Eq. (11), if △(x)P_i+△(x–L)P_i is assumed as the volume force in the x direction, then the longitudinal stress of layer i should correspond to 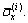In this case, the constitutive relations are

,

,

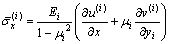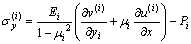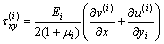                (13)

The governing equation can be derived from Eqs. (11) and (13) as follows:

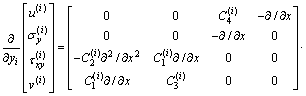
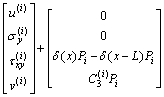            (14)

where

, , ,

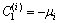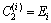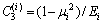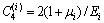                         (15)

4 General solutions of arbitrary layer

The Dirac delta functions △(x) and △(x–L) in Eq. (14) can be expanded into the Fourier cosine series as follows:

,

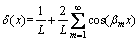           (16)

where β_m=mπ/L. The solutions of displacements and stresses are assumed to be

,

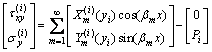         (17)

where U(i) m(y_i), V(i) m(y_i), X(i) m(y_i)and Y(i) m(y_i) are the undetermined functions. Substituting the solutions of u⁽ⁱ⁾ and σ(i) y in Eq. (17) into the stress component 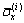in Eq. (13), one can express 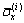in terms of U(i) m(y_i) and Y(i) m(y_i) by

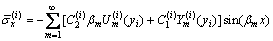 (18)

Accordingly, σ(i) x can be obtained by applying the solution of 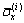to Eq. (9). From the solution forms of v⁽ⁱ⁾ and σ(i) x, it is obvious that the boundary conditions Eq. (6) are exactly satisfied.

Applying Eqs. (16) and (17) to Eq. (14) for each term m gives

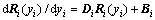                 (19)

where

,

,

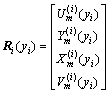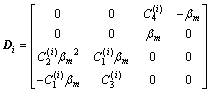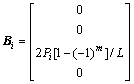                    (20)

where R_i(y_i) and D_i are the state vector and system matrix of layer i, respectively. It is clear that Eq. (19) consists of four first-order differential equations with respect to the coordinate y_i. Note that the system matrix D_i is a constant matrix for the homogeneous isotropic material of layer i.

The solution of Eq. (19) is

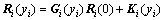                (21)

where G_i(y_i)=exp(D_iy_i) is the state transition matrix of layer i. R_i(0) is the magnitude of R_i(y_i) at y_i=0. 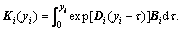Applying the Cayley-Hamilton theorem to the matrix exponential exp(D_iy_i), we have

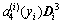                           (22)

where a(i) j(y_i) (j=1, 2, 3, 4) are a set of scalar functions dependent on the eigenvalues of D_i. I is a 4×4 unit matrix. From the second of Eq. (20), one can easily obtain the eigenvalues λ of the matrix D_i as follows:

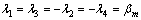                   (23)

i.e., the matrix D_i has repeated eigenvalues. a(i) j(y_i) are given by

 (24)

Solving a(i) j(y_i) from the above equation and substituting them into Eq. (22), the solutions of G_i(y_i) and K_i(y_i) are obtained. Finally, the state vector R_i(y_i) can be obtained by substituting G_i(y_i) and K_i(y_i) into Eq. (21).

From Eq. (23), it is concluded that for isotropic materials, the system matrix has repeated eigenvalues. However, for anisotropic materials another form of Eq. (24) can be given for no repeated eigenvalues, which is not discussed here.

5 Elasticity solutions of laminated beam

5.1 Recursive formulas for displacements and stresses

Equation (21) is available to every layer of the laminated beam. Without loss of generality, two adjacent layers i and i+1 are considered. Taking y_i=h_i and y_i+1=h_i+1 into Eq. (21) results in the following two equations:

,

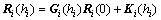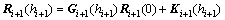       (25)

Applying the Fourier series expansion to the isotropic normal stress P_i in Eq. (17) gives

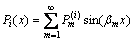                    (26)

where 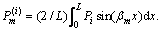Applying Eqs. (17) and (26) to Eq. (8), the interfacial continuity conditions are rewritten in the compact form of

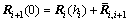                    (27)

where 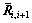=[0 P⁽ⁱ⁺¹⁾_m P⁽ⁱ⁾_m 0 0]^T.

From Eqs. (25) and (27), the relation between the two adjacent layers is

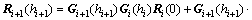
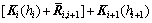              (28)

Therefore, the relation between layer k and the bottom layer can be recursively derived:

,

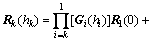
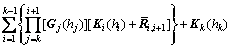(k=1, 2, …, p)                      (29)

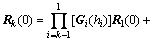
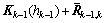,(k=2, 3, …, p)      (30)

5.2 Unknowns in solutions

Similarly, applying the Fourier series expansion to the transverse loads q₁(x) and q₂(x) in Eq. (7) respectively gives

,

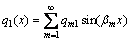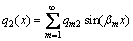                    (31)

where 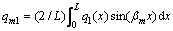and 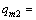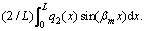Applying Eqs. (17), (26) and (31) to Eq. (7), the top and bottom surface conditions are rewritten as

,

,

,

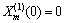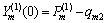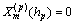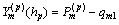                      (32)

Substituting Eq. (32) into Eq. (29) gives the relation between the top and bottom layers as follows:

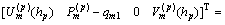
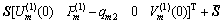    (33)

where

,

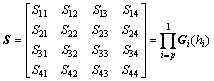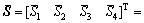
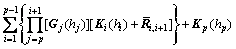  (34)

It is noted that S is a 4×4 constant matrix and S is a 4×1 constant column vector. Therefore, Eq. (33) consists of four linear algebraic equations with four unknowns U(p) m(h_p), V(p) m(h_p), U(1) m(0) and V(1) m(0). Decomposing Eq. (33) into two groups of equations, one group equation is

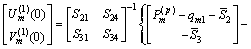
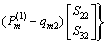                     (35)

Therefore, R₁(0) can be obtained when U(1) m(0) and V(1) m(0) are determined. Substituting R₁(0) into Eq. (30), R_i(0) (i=1, 2, …, p) can be solved. Substituting R_i(0) into Eq. (21) obtains the state vector R_i(y_i) for an arbitrary layer. Finally, the displacements and stresses u⁽ⁱ⁾, v⁽ⁱ⁾, σ(i) y and τ(i) xy are solved by applying R_i(y_i) to Eqs. (17) and (18), and the longitudinal normal stress σ(i) x can be solved from Eq. (9).

6 Convergence and comparison studies

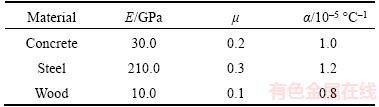
According to the above analysis, a computer code is written to calculate the solutions. The FE solutions using ANSYS software are compared with the present solutions. The PLANE-183 element is used in the FE simulation. In the following examples, all the material properties are adopted according to Table 1 unless stated and the temperature dependence of material properties is ignored.

Table 1 Material properties of concrete, steel and wood

6.1 Convergence study

It is well known that the cracks of the concrete beam are commonly aroused by the tension stress generated near the surfaces, which can be improved by externally bonding thin steel face sheets with higher tensile strength and ductility. We consider a three-layer beam composed of concrete core and steel face sheets. The geometric parameters of the three-layer beam are respectively given by: L=4 m, h₁=0.05 m, h₂=0.9 m, h₃=0.05 m. The beam is under a mechanical load q₁(x)=5 kN/m on its top surface. The uniform temperature field has the increment △T=100 °C.

The displacements and stresses can be numerically solved by truncating the terms of the series m up to N, i.e., m=1, 2, …, N. Table 2 lists the displacement and stress components at two points for different truncated terms. The results shown in the table indicate that the present solutions converge well and obtain satisfactory accuracy as N increases. The rates of convergence are different between the two points. Note that the truncated terms of the series are finite in the computation, due to the restricted speed and computational accuracy of computer.

6.2 Comparison study

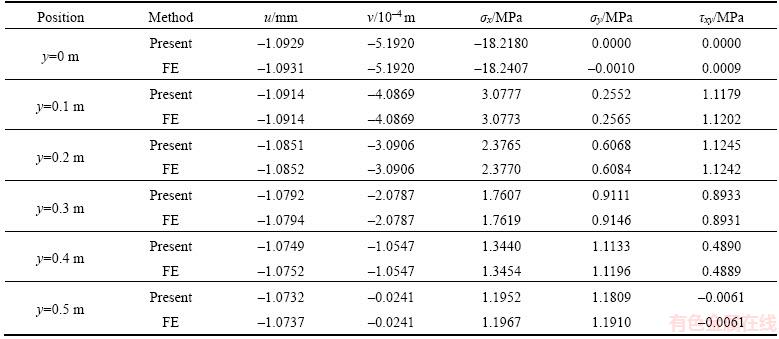
Consider the above three-layer beam. Table 3 gives the comparative study between the present elasticity solutions and the FE solutions about the displacements and stresses at six equidistant points. The results given in Table 3 validate that the displacements and stresses calculated by the present 2-D elasticity solutions match well with those from the FE software. The relative errors are less than 1% except for the transverse stress and shear stress at x=1 m, y=0 m, since the FE solutions of some stress components at boundary points are less accurate.

Table 2 Convergence study of displacements and stresses for three-layer beam under thermo-mechanical loads, q₁(x)=5 kN/m and △T=100 °C

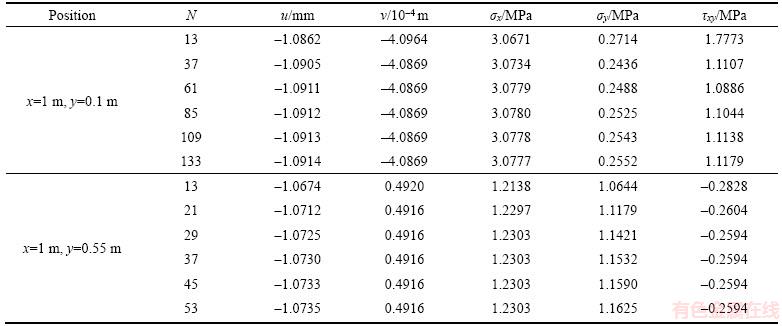
Table 3 Comparison study of displacements and stresses at x=1 m for three-layer beam under thermo-mechanical loads, q₁(x)=5 kN/m and △T=100 °C

The present elasticity solutions are further compared with the available Timoshenko’s solutions [17]. Timoshenko presented the curvature of a two-layer strip under uniform thermo-load as follows:

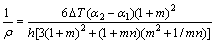         (36)

where the coefficients m=h₁/h₂, n=E₁/E₂, h=h₁+h₂. ρ is the radius of the curvature. Thus, the maximum deflection of the strip is v_m=L²/8ρ. Consider a two-layer beam subjected to a uniform temperature field with the increment △T=100 °C. The upper and lower layers of the beam are made up of concrete and wood, respectively. The length L is variable, while the thickness of each layer is h₁=h₂=0.1 m. Figure 2 indicates the comparisons among the present elasticity solutions, the Timoshenko’s solutions and the FE solutions about the transverse displacement v at x=0.5L, y=0.5H with respect to the length-to-thickness ratio L/H. From Figure 2, it is shown that the FE results fit well with the present elasticity solutions. Meanwhile, for slender beams, the present elasticity solutions and the Timoshenko’s solutions show good agreements. However, as L/H decreases the difference enlarges gradually and the relative error reaches 12.8% when L/H=4.

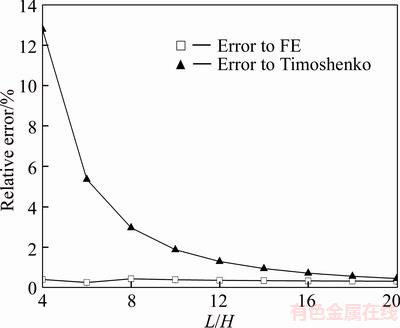
Figure 2 Comparison study of transverse displacement v at x=0.5L, y=0.5H with respect to length-to-thickness ratio L/H for two-layer beam under uniform thermo-load △T=100 °C (Error to FE means: (FE–present)/present); Error to Timoshenko means: (Timoshenk–present)/ present))

7 Effects of material properties variable with temperature

In general, temperature change could result in the variation of material properties, thereby affecting the structure behavior. Therefore, it is of great importance for structural safety to take into account the temperature dependence of material properties in engineering. The following two examples are provided to study the effects of material properties variable with temperature on the displacement and stress distributions in the laminated beams. Based on the regression analysis from Chang et al [8] and Yang et al [9], the relations between elastic modulus and temperature for steel and concrete are respectively:

,

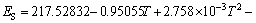
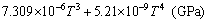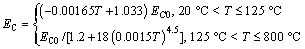(37)

where E_S and E_C are the elastic moduli of steel and concrete, respectively. E_C0=30 GPa is the elastic modulus of concrete at T=20 °C. Based on the regression analysis from Li et al [10], the relation between thermal expansion coefficient and temperature for steel is:

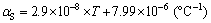         (38)

where α_s is the thermal expansion coefficient of steel. The thermal expansion coefficient of concrete and the Poisson ratios of the two materials are considered to be constants as given in Table 1, since they change very little with temperature. In the following examples, the displacements and stresses are calculated based on two cases: 1) the material properties are considered to be temperature- dependent (TD); 2) the material properties are considered to be temperature-independent (TI), i.e., the material properties of steel and concrete are constants, which are taken as those at T=T₀.

7.1 Two-layer beam under different temperatures

Consider a two-layer beam with the upper and lower layers respectively made by concrete and steel. The geometric parameters are respectively given by: L=3 m, h₁=0.05 m and h₂=0.55 m. The uniform temperature in the stress-free state is T₀= 20 °C. The top surface of the beam is under a transverse load q₁(x)=5sin(πx/L) kN/m. Meanwhile, the beam is subjected to three different temperature increments: △T=50 °C, 100 °C, 150 °C, i.e., the temperature fields in the final state are T=70 °C, 120 °C, 170 °C, respectively. Figure 3 shows the through-thickness distributions of u, v, σ_x and τ_xy at x=L/6 for different temperatures. It can be found in Figure 3 that the displacement and stress distributions have significant changes between cases TD and TI. In the case of TI, u, v, σ_x and τ_xy increase with the rise of temperature T. However, in case of TD, the correlations of temperature with displacements and stresses are irregular, which are greatly affected by the relations between the material properties and temperature. We can see from Figure 3(d) that the shear stress τ_xy takes zero value at y/H=0 and y/H=1, which exactly satisfies the boundary conditions Eq. (7). Additionally, from Figure 3(c), it is noticed that the longitudinal stress σ_x has a sudden change on the interface, which is due to the different material properties between concrete and steel.

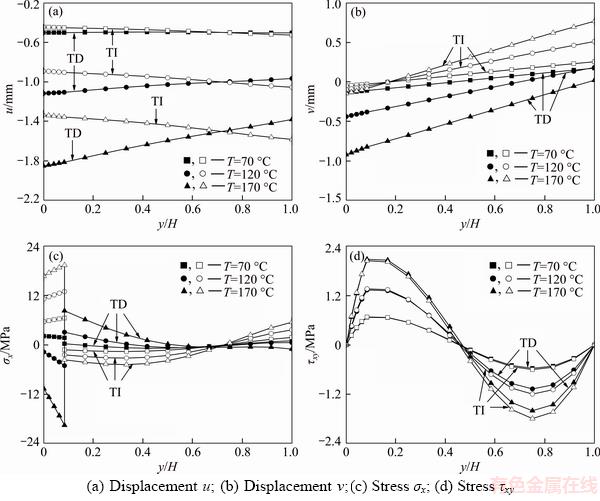
Figure 3 Through-thickness distributions of displacements and stresses at x=L/6 for two-layer beam under distributed load q₁(x)=5sin(πx/L) and different thermo-loads △T=50 °C, 100 °C, 150 °C:

For further comparing the displacements between cases TD and TI, the variations of displacements at x=0.5 m, y=0.05 m with temperature are plotted in Figure 4. According to Figures 4(a) and (b), it is seen that u and v both increase linearly in case of TI while they nonlinearly rise in case of TD as temperature rises because that the material properties change with temperature in case TD but keep constant in case TI.

7.2 Three-layer beam with different length-to- thickness ratios

Consider a three-layer beam composed of concrete core and steel face sheets. The beam is subjected to a linearly distributed transverse load q₁(x)=x+2 kN/m on the top surface. The uniform temperature fields in the stress-free and final states are given by T₀=20 °C and T=120 °C, respectively. Some geometric parameters are respectively given by: L=6 m, h₁=h₃=0.1H and h₂=0.8H. Figure 5 displays the through-thickness distributions of u, v, σ_x and τ_xy at x=1.5 m for three length-to-thickness ratios L/H=4, 5, 6, i.e., the beam thickness H=1.5 m, 1.2 m, 1 m. As shown in Figure 5(a), the distribution of u in case TD is larger in magnitude than that in case TI. The distribution of u is close to a constant value as L/H increases. According to Figures 5(b) and (d), v and τ_xy are increased by decreasing L/H. Figure 5(c) shows the difference of σ_x between the two cases. In the concrete core, the variation of σ_x is insignificant as L/H increases.

8 Conclusions

The elasticity solution of simply-supported laminated beams with material properties variable with temperature under a combination of uniform thermo-load and mechanical loads is investigated. The solutions of displacements and stresses are deduced from the elasticity equations. The present solutions exactly meet the boundary conditions and the interfacial continuity conditions. The effects of material properties variable with temperature on the behavior of the laminated beams are studied. The main findings of this study are summarized as follows:

1) For the slender beams, the present elasticity solution and the classical solution show good agreements. However, for the thick beams, the difference is significant between the two solutions. Since the classical analysis is based on the Euler-Bernoulli beam theory which ignores the transverse shear effect. However, the present analysis based on the elasticity theory can give accurate solution for both slender beams and thick beams, since the elasticity theory has no any hypothesis.

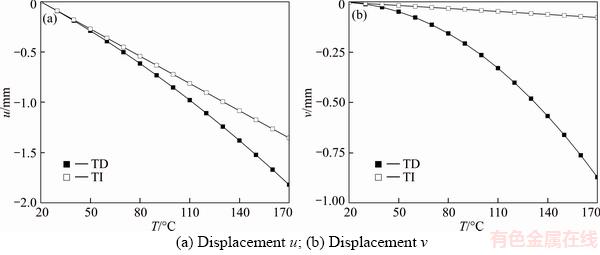
Figure 4 Variations of displacements at point of x=0.5 m, y=0.05 m with respect to temperature for a two-layer beam under a distributed load q₁(x)=5sin(πx/L) and different thermo-loads:

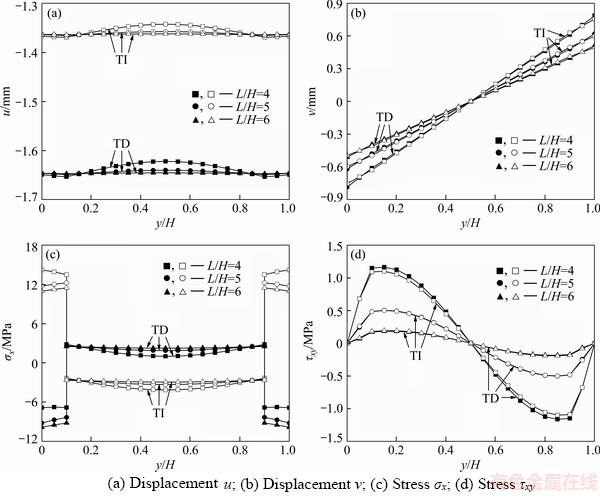
Figure 5 Through-thickness distributions of displacements and stresses at x=1.5 m for three-layer beam under thermo-mechanical loads (q₁(x)=x+2, △T=100 °C) for different length-to-thickness ratios L/H=4, 5, 6:

2) The FE solutions match well with the present solutions. However, the FE simulation possesses some disadvantages comparing to the present analysis: 1) the accuracy of the solution is directly affected by the mesh density; 2) the computation is time consuming; 3) Making the parametric study is difficult.

3) The displacement and stress components linearly increase as temperature rises when considering the material properties to be temperature-independent. However, once the material properties vary with temperature, the correlations of temperature with displacement and stress components are irregular.

4) The transverse displacement v and shear stress τ_xy are increased by decreasing the length- to-thickness ratio L/H. The longitudinal stress σ_x has a sudden change when passing from one layer to another, due to the different material properties between adjacent layers.

5) The present analysis focuses on the laminated beams with simply-supported ends. The analytical method can be extended to beams with other boundary conditions. The present analysis can also be employed to investigate the thermo-elastic behavior of the FGM structures by introducing the approximate laminate model. Moreover, the present analysis can be extended from two-dimensional problem to three-dimensional problem.

References

[1] FORABOSCHI P. Hybrid laminated-glass plate: Design and assessment [J]. Composite Structures, 2013, 106: 250–263. DOI: 10.1016/j.compstruct.2013.05.041.

[2] SPERANZINI E, AGNETTI S. Strengthening of glass beams with steel reinforced polymer (SRP) [J]. Composites Part B: Engineering, 2014, 67: 280–289. DOI: 10.1016/ j.compositesb.2014.06.035.

[3] JHA D K, KANT T, SINGH R K. A critical review of recent research on functionally graded plates [J]. Composite Structures, 2013, 96: 833–849. DOI: 10.1016/j.compstruct. 2012.09.001.

[4] LIU Wu-xiang. Analysis of steady heat conduction for 3D axisymmetric functionally graded circular plate [J]. Journal of Central South University, 2013, 20(6): 1616–1622. DOI: 10.1007/s11771-013-1654-0.

[5] SU H, BANERJEE J R, CHEUNG C W. Dynamic stiffness formulation and free vibration analysis of functionally graded beams [J]. Composite Structures, 2013, 106: 854–862. DOI: 10.1016/j.compstruct.2013.06.029.

[6] TRINH L C, VO T P, THAI H T, NGUYEN T K. An analytical method for the vibration and buckling of functionally graded beams under mechanical and thermal loads [J]. Composites Part B: Engineering, 2016, 100: 152–163. DOI: 10.1016/j.compositesb.2016.06.067.

[7] ABBAS I A. Generalized thermoelastic interaction in functional graded material with fractional order three-phase lag heat transfer [J]. Journal of Central South University, 2015, 22(5): 1606–1613. DOI: 10.1007/s11771-015-2677-5.

[8] Chang Y F, Chen Y H, Sheu M S, YAO G C. Residual stress-strain relationship for concrete after exposure to high temperatures [J]. Cement and Concrete Research, 2006, 36(10): 1999–2005. DOI: 10.1016/j.cemconres.2006.05.029.

[9] Yang Xiu-ying, Zhao Jin-cheng. Experimental study on stress-strain-temperature models for structural steel [J]. Journal of Harbin Institute of Technology (New Series), 2011, 18(1): 6–10. DOI: 10.11916/j.issn.1005-9113.2011.01.002.

[10] LI Guo-qiang, JIANG Shou-chao, YIN Ying-zhi, CHEN Kai, LI Ming-fei. Experimental studies on the properties of constructional steel at elevated temperatures [J]. Journal of Structural Engineering, 2003, 129(12): 1717–1721. DOI: 10.1061/(ASCE)0733-9445(2003)129:12(1717).

[11] TAUCHERT T R. Thermally induced flexure, buckling, and vibration of plates [J]. Applied Mechanics Reviews, 1991, 44(8): 347–360. DOI: 10.1115/1.3119508.

[12] GHUGAL Y M, SHIMPI R P. A review of refined shear deformation theories of isotropic and anisotropic laminated beams [J]. Journal of Reinforced Plastics and Composites, 2001, 20(3): 255–272. DOI: 10.1106/N95G-ERA1-A1CM- RD7E.

[13] GHUGAL Y M, SHIMPI R P. A review of refined shear deformation theories of isotropic and anisotropic laminated plates [J]. Journal of Reinforced Plastics and Composites, 2002, 21(9): 775–813. DOI: 10.1177/073168402128988481.

[14] REDDY J N, ARCINIEGA R A. Shear deformation plate and shell theories: From Stavsky to present [J]. Mechanics of Advanced Materials and Structures, 2004, 11(6): 535–582. DOI: 10.1080/15376490490452777.

[15] CARRERA E, BRISCHETTO S. A survey with numerical assessment of classical and refined theories for the analysis of sandwich plates [J]. Applied Mechanics Reviews, 2009, 62(1): 010803. DOI: 10.1115/1.3013824.

[16] SAYYAD A S, GHUGAL Y M. Bending, buckling and free vibration of laminated composite and sandwich beams: A critical review of literature [J]. Composite Structures, 2017, 171: 486–504. DOI: 10.1016/j.compstruct.2017.03.053.

[17] TIMOSHENKO S. Analysis of bi-metal thermostats [J]. Journal of the Optical Society of America, 1925, 11(3): 233–255. DOI: 10.1364/JOSA.11.000233.

[18] MOHANDES M, GHASEMI A R. Modified couple stress theory and finite strain assumption for nonlinear free vibration and bending of micro/nanolaminated composite Euler-Bernoulli beam under thermal loading [J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2016, 231(21): 4044–4056. DOI: 10.1177/0954406216656884.

[19] FU Y, WANG J, HU S. Analytical solutions of thermal buckling and postbuckling of symmetric laminated composite beams with various boundary conditions [J]. Acta Mechanica, 2014, 225(1): 13–29. DOI: 10.1007/s00707- 013-0941-z.

[20] MORADI S, MANSOURI M H. Thermal buckling analysis of shear deformable laminated orthotropic plates by differential quadrature [J]. Steel and Composite Structures, 2012, 12(2): 129–147. DOI: 10.12989/scs.2012.12.2.129.

[21] SHATERZADEH A R, ABOLGHASEMI S, REZAEI R. Finite element analysis of thermal buckling of rectangular laminated composite plates with circular cut-out [J]. Journal of Thermal Stresses, 2014, 37(5): 604–623. DOI: 10.1080/ 01495739.2014.885322.

[22] HAN J W, KIM J S, CHO M. New enhanced first-order shear deformation theory for thermo-mechanical analysis of laminated composite and sandwich plates [J]. Composites Part B, 2017, 116: 422–450. DOI: 10.1016/j.compositesb. 2016.10.087.

[23] KHDEIR A A, REDDY J N. Thermal stresses and deflections of cross-ply laminated plates using refined plate theories [J]. Journal of Thermal Stresses, 1991, 14(4): 419–438. DOI: 10.1080/01495739108927077.

[24] NAJAFIZADEH M M, HEYDARI H R. Thermal buckling of functionally graded circular plates based on higher order shear deformation plate theory [J]. European Journal of Mechanics-A/Solids, 2004, 23(6): 1085–1100. DOI: 10.1016/j.euromechsol.2004.08.004.

[25] SINGH S, SINGH J, SHUKLA K K. Buckling of laminated composite plates subjected to mechanical and thermal loads using meshless collocations [J]. Journal of Mechanical Science and Technology, 2013, 27(2): 327–336. DOI: 10.1007/s12206-012-1249-y.

[26] Kapuria S, Dumir P C, Ahmed A. An efficient higher order zigzag theory for composite and sandwich beams subjected to thermal loading [J]. International Journal of Solids and Structures, 2003, 40(24): 6613–6631. DOI: 10.1016/j.ijsolstr.2003.08.014.

[27] GHUGAL Y M, KULKARNI S K. Thermal response of symmetric cross-ply laminated plates subjected to linear and non-linear thermo-mechanical loads [J]. Journal of Thermal Stresses, 2013, 36(5): 466–479. DOI: 10.1080/ 01495739.2013.770664.

[28] GHUGAL Y M, KULKARNI S K. Flexural analysis of cross-ply laminated plates subjected to nonlinear thermal and mechanical loadings [J]. Acta Mechanica, 2013, 224(3): 675–690. DOI: 10.1007/s00707-012-0774-1.

[29] SAYYAD A S, SHINDE B M, GHUGAL Y M. Thermoelastic bending analysis of orthotropic plates using hyperbolic shear deformation theory [J]. Composites: Mechanics, Computations, Applications: An International Journal, 2013, 4(3): 257–278. DOI: 10.1615/ CompMechComputApplIntJ.v4.i3.50.

[30] SAYYAD A S, GHUGAL Y M., MHASKE B A. A four-variable plate theory for thermoelastic bending analysis of laminated composite plates [J]. Journal of Thermal Stresses, 2015, 38(8): 904–925. DOI: 10.1080/01495739. 2015.1040310.

[31] Xu Ye-peng, Zhou Ding. Two-dimensional thermoelastic analysis of beams with variable thickness subjected to thermo-mechanical loads [J]. Applied Mathematical Modelling, 2012, 36(12): 5818–5829. DOI: 10.1016/j.apm. 2012.01.048.

[32] Qian Hai, Zhou Ding, Liu Wei-qing, FANG Hai. Elasticity solution of laminated beams subjected to thermo-loads [J]. Journal of Central South University, 2015, 22: 2297–2305. DOI: 10.1007/s11771-015-2754-9.

[33] QIAN Hai, ZHOU Ding, LIU Wei-qing, FANG Hai, LU Wei-dong. 3-D elasticity solutions of layered rectangular plates subjected to thermo-loads [J]. Journal of Thermal Stresses, 2015, 38(4): 377–398. DOI: 10.1080/01495739. 2014.985570.

[34] LV Chao-feng, CHEN Wei-qiu, ZHONG Zheng. Two- dimensional thermoelasticity solution for functionally graded thick beams [J]. Science in China Series G: Physics, Mechanics and Astronomy, 2006, 49(4): 451–460. DOI: 10.1007/s11433-006-0451-2.

[35] Pilipchuk V N, Berdichevsky V L, Ibrahim R A. Thermo-mechanical coupling in cylindrical bending of sandwich plates [J]. Composite Structures, 2010, 92(11): 2632–2640. DOI: 10.1016/j.compstruct.2010.03.007.

[36] Alibeigloo A. Thermo elasticity solution of sandwich circular plate with functionally graded core using generalized differential quadrature method [J]. Composite Structures, 2016, 136: 229–240. DOI: 10.1016/j.compstruct.2015. 10.012.

(Edited by HE Yun-bin)

中文导读

均匀热载荷和机械载荷共同作用下具有温度依赖材料特性的层合梁的弹性力学解

摘要：本文基于二维热弹性力学理论，考虑材料物性参数的温度依赖性，研究了均匀热荷载和机械荷载联合作用下简支叠层梁的精确解。首先将叠层梁沿各组分材料的界面划分为一系列单层，以保证每一单层材料的物理性能均匀。利用等效模型，将作用在单层内的均匀热荷载转化为作用于层两端的法向面力和横向热荷载。其次，利用状态空间法求得任一层内位移和应力的一般解。第三，根据相邻层界面的连续性条件，使用传递矩阵法递推得到顶层和底层位移和应力的关系，由作用于梁上下表面的机械荷载确定未知系数。研究了本文解的收敛性，并给出了与Timoshenko的解和有限元解的比较。最后通过数值算例，详细分析了随温度变化的材料物理参数对叠层梁力学性能的影响。

关键词：层合梁；热弹性力学；解析解；传递矩阵法；温度依赖材料

Foundation item: Project(2012CB026205) supported by the National Basic Research Program of China; Projects(51608264, 51778289) supported by the National Natural Science Foundation of China; Project(2014Y01) supported by the Transportation Science and Technology Project of Jiangsu Province, China

Received date: 2017-08-22; Accepted date: 2017-12-06

Corresponding author: ZHOU Ding, PhD, Professor; Tel: +86-25-58139863; E-mail: dingzhou57@yahoo.com; ORCID: 0000-0003- 1556-2092