


Trans. Nonferrous Met. Soc. China 22(2012) 432-441
Support vector machines approach to mean particle size of rock fragmentation due to bench blasting prediction
SHI Xiu-zhi1, ZHOU Jian1, WU Bang-biao1, 2, HUANG Dan1, WEI Wei1
1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;
2. Department of Civil Engineering, University of Toronto, Toronto M4Y 1R5, Canada
Received 28 March 2011; accepted 1 August 2011
Abstract: Aiming at the problems of the traditional method of assessing distribution of particle size in bench blasting, a support vector machines (SVMs) regression methodology was used to predict the mean particle size (X50) resulting from rock blast fragmentation in various mines based on the statistical learning theory. The data base consisted of blast design parameters, explosive parameters, modulus of elasticity and in-situ block size. The seven input independent variables used for the SVMs model for the prediction of X50 of rock blast fragmentation were the ratio of bench height to drilled burden (H/B), ratio of spacing to burden (S/B), ratio of burden to hole diameter (B/D), ratio of stemming to burden (T/B), powder factor (Pf), modulus of elasticity (E) and in-situ block size (XB). After using the 90 sets of the measured data in various mines and rock formations in the world for training and testing, the model was applied to 12 another blast data for validation of the trained support vector regression (SVR) model. The prediction results of SVR were compared with those of artificial neural network (ANN), multivariate regression analysis (MVRA) models, conventional Kuznetsov method and the measured X50 values. The proposed method shows promising results and the prediction accuracy of SVMs model is acceptable.
Key words: rock fragmentation; blasting; mean particle size (X50); support vector machines (SVMs); prediction
1 Introduction
Rock fragmentation, the fragment size distribution of blasted rock, is considered one of the most significant indices of production blasting because of its direct effects on the costs of drilling and blasting and on the economics of the subsequent operations of loading, hauling and crushing [1-3]. The key objective of production blasting is to achieve optimum rock fragmentation and control the particle size distribution of a muckpile after blasting. Improvement of blasting results provides increase in loader and excavator productivity due to increased diggability capacity, and increased bucket and truck fill factors. Suitable and uniform particle size distribution lead to increase in crusher and mill throughput and decrease in energy consumption in size reduction process. Additionally, uniform particle size distribution also eliminates the need of the secondary blasting of the big boulders [4, 5].
Over the past three decades, empirical models for the estimation of size distribution of rock fragments have been developed [6-10]. KUZNETSOV [6] formulated a semi-empirical equation based on field investigations and a review of previously published data that related the mean fragment size to the mass of explosive, the volume blasted and the rock strength. The Kuz–Ram fragmentation model was developed by CUNNINGHAM [7] based on the Kuznetsov and Rosin–Rammler equations as well as an algorithm. The Rosin–Rammler equation proposed by ROSIN and RAMMLER [8] was used to characterize the partial-size distribution of a material for use in a variety of applications. GHEIBIE et al [9] established a modified Kuz–Ram fragmentation model and used it at the Sungun Copper Mine. But regards to inconstant situations in practice such as existence of underground waters, sudden change of geological structure, blasting pattern size, several blasting must be tested frequently, which is expensive and time consuming. Therefore, operational and capital costs are increased, and the system is no longer profitable. Sieve analysis [10] and image analysis [11, 12] of rock fragmentation have been used in mines and quarries to control the quality of blasting and measure blast fragmentation distribution. However, because muck piles are large, use of sieve analysis is tedious and time consuming and thus not practicable for measurement of blast fragmentation distribution of muck piles.
Rock fragmentation depends on many variables such as rock mass properties, site geology, in situ fracturing and blasting parameters, and as such has no complete theoretical solution for its prediction. In such situations, a wide range of statistical and machine learning models have been developed and applied in this field to measure the fragmentation distribution and predict X50 resulting from rock blast fragmentation [4, 5, 13-16]. Multivariate regression analysis (MVRA) was used to develop fragmentation prediction models by ALER et al [13] and HUDAVERDI et al [14] taking into account of intact and joints rock properties, the type and properties of explosives and the drilling pattern. A blast fragmentation Monte Carlo-based simulation program proposed by MARIO and FRANCESCO [15], based on the Kuz–Ram fragmentation model, was developed to predict the entire fragmentation size distribution. MONJEZI et al [16] proposed a fuzzy logic model to predict fragmentation caused by blasting at Gol-E-Gohar iron mine. MONJEZI et al [4] and KULATILAKE et al [5] developed a neural network methodology to predict X50 resulting from rock blast fragmentation with regards to the existence situations and the practical data.
Among artificial intelligence (AI) tools, the artificial neural network (ANN) approach has been recently applied to developing predictive rock fragmentation models which have provided significant improvements in accuracy compared with the multi- variate regression based models [4, 17-26]. Support vector machines (SVMs) are another efficient machine learning (ML) technique derived from statistical learning theory by VAPNIK [17]. However, since the middle of 1990s, the algorithms used for SVMs have been emerged with greater availability of geotechnical practice and mining science [18-23], paving the way for numerous practical applications. It is therefore motivative to investigate the capability of SVMs in mean particle size (X50) resulting from rock blast fragmentation prediction.
The current research tries to explore the feasibility of a regression of SVMs model to predict X50 of rock fragmentation due to blasting in several mines. The theory and procedure of SVMs are briefly reviewed. The development of SVMs based on rock fragmentation models is presented and the performance of predictive models is discussed.
2 Regression theory of SVMs
2.1 Basic idea of SVR model
SVMs [17, 24] have been introduced as an effective model in both ML and data mining communities for solving both classification and regression problems. Support vector regression (SVR) is a powerful ML method that is useful for constructing data-driven non-linear empirical process models. It shares many features with ANNs but possesses some additional desirable characteristics and is gaining widespread acceptance in data-driven non-linear modeling applications. Comprehensive tutorials on SVMs for regression are available in many sources. Brief summary of the SVR theory for regression is given here primarily based on GOPALAKRISHNAN and KIM [19], SAMUI et al [21], ZHOU et al [22, 23], GUNN [24], LI [25] and CHANG et al [26].
The basic concept of SVR is to map nonlinearly the original data x into a higher dimensional feature space and solve a linear regression problem in this feature space [17–26]. First, we use a linear function to regress the data set  , where xi is the input vector to the SVR model, yi is the actual output value, from which it learns the input–output relationship, and p denotes the total number of data patterns. The SVMs regression model can be expressed as [17,22-24]:
, where xi is the input vector to the SVR model, yi is the actual output value, from which it learns the input–output relationship, and p denotes the total number of data patterns. The SVMs regression model can be expressed as [17,22-24]:
 (1)
(1)
where the function φ(x) denotes the high dimensional kernel-induced feature space, the parameters w and b are a support vector weight vector and a bias term that are calculated by minimizing the following regularized risk function:
 (2)
(2)
where C denotes a cost function measuring the empirical risk; ||w||2/2 denotes the regularization term; ρε(yi, f(xi)) is called the ε-insensitive loss function, which is defined as:
 (3)
(3)
In Eq. (3), the loss equals zero if the error of forecasting value is less than ε, otherwise the loss is beyond ε.
Two positive slack variables, ξi and ξi*, i = 1, 2, …, n, can be used to measure the deviation (qi - f(xi)) from the boundaries of the ε-insensitive zone. That is, they represent the distance from actual values to the corresponding boundary values of ε-insensitive zone. By using slack variables, Eq. (2) is transformed into the following constrained form:
Minimize:
 (4)
(4)
subject to 
By using Lagrangian multipliers and Karush– Kuhn–Tucker (KKT) conditions to Eq. (4), it thus yields the following dual Lagrangian form [17,24],
Maximize:

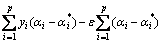 (5)
(5)
subject to the constraints,
 (6)
(6)
The Lagrangian multipliers in Eq. (6) satisfy the equality αiαi*=0. The Lagrangian multipliers, αi and αi*, are calculated and an optimal desired weight vector of the regression hyperplan is obtained by 
 Hence, the general form of the SVMs-based regression function can be written as [17,24]:
Hence, the general form of the SVMs-based regression function can be written as [17,24]:
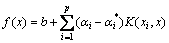 (7)
(7)
Based on the KKT conditions of solving quadratic programming problem, (αi- ) in Eq. (7), only some of them will be held as non-zero values. According to Eq. (7), it is evident that support vectors are only used in determining the decision function since the coefficients (αi-
) in Eq. (7), only some of them will be held as non-zero values. According to Eq. (7), it is evident that support vectors are only used in determining the decision function since the coefficients (αi- ) of other data points are all equal to zero. In Eq. (7), K(xi, x) is called the kernel function. The concept of kernel function K(xi, x)=Φ(xi)·Φ(x) has been introduced to reduce the computational demand [18].
) of other data points are all equal to zero. In Eq. (7), K(xi, x) is called the kernel function. The concept of kernel function K(xi, x)=Φ(xi)·Φ(x) has been introduced to reduce the computational demand [18].
In SVMs, typical common kernels described in GUNN [18] have been used, such as polynomial, radial basis function (RBF), Gaussian function, multilayer perceptron, sigmoid, for non-linear cases. In this way, a nonlinear model in the original space can be transformed to the linear model in the new space. In the present work, SVMs constructed by RBF kernel which is given by Eq. (8) is used because it yields better forecasting performance[17,25,26].
K(x, y)=exp(-|x-y|2/2g2) (8)
where g denotes the width of the RBF.
Here, C, g and ε are user-determined parameters by an iterative process selecting an optimum value based on the full training data set. The election of the parameters plays an important role in the performance of SVMs. Further detailed mathematical description over SVR can be referred from Refs. [17-26].
2.2 SVMs model computational procedure
The approach for the development of the SVR-based correlation can be divided into five stages: 1) Collection of data sets, which have been divided into two sub-sets, namely, a training dataset and a testing dataset; 2) Linear scaling of the train data set from 0 to 1, calculation of the various parameters (model parameters) for establishing the regression function; 3) Estimation of the optimal model parameters (C, g, ε) using the combined approach of K-fold cross validation and grid search method (GSM) [22,23,27]; 4) Establishment of the final SVR model for X50 of rock blast fragmentation with the help of the best parameters; 5) Evaluation and validation of the SVR model by evaluation with testing data and comparing it with literature correlations. For better understanding, a flow diagram describing the establishment of the SVR-based model for prediction X50 resulting from rock blast fragmentation is shown in Fig. 1.
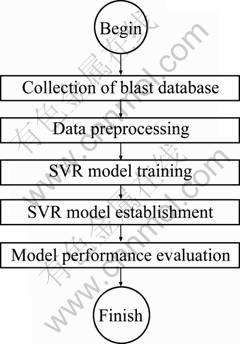
Fig. 1 Flowchart of key steps for establishment of SVR model
3 Experimental studies for forecasting X50 of rock blast fragmentation based on SVR
3.1 Collection of data set
In the present study, the blast database is taken from HUDAVERDI et al’s results [5, 14] collected in various mines and rock formation in the world, as given in Table 1 [5,14]. A total of 90 blasts shown in Table 1 are evaluated to form a blast database. The blasts shown by symbols ‘Rc’, ‘En’ and ‘Ru’ were collected from HAMDI et al [2] and ALER et al [3] research conducted at the Enusa and Reocin mines, which are located in Spain. The Enusa Mine is an open-pit uranium mine in a schistose and is a moderately to heavily folded formation. The Reocin mine is an open-pit and underground zinc mine. The blasts shown by symbol ‘Mg’ were performed in the Murgul Copper Mine, which is a large open-pit mine located in the Northeastern Turkey [28]. The blasts shown by symbol ‘Mr’ were obtained from OUCHTERLONY et al’s [29] research performed in the Mrica Quarry in Indonesia. The blasts indicated with ‘Db’ symbol were performed in the Dongri-Buzurg open-pit manganese mine situated in Central India [30]. The blasts indicated with symbol ‘Sm’ were performed in an open-pit coal mine in Soma Basin, which is located in Western Turkey [31]. The blasts shown by symbols ‘Ad’ and ‘Oz’ were performed at the Akdaglar and Ozmert Quarries of Cendere basin located in the northern Istanbul [5, 14]. The scatter plot matrix of the original data set is given in Fig. 2. No obvious correlation among the variables is observed. For implementing the SVR, the data are divided into two sub-sets:
Table 1 Samples of training for rock fragmentation analysis of some projects around the world [5, 14]

1) A training dataset. This is required to train the model. In this study, 90 out of a total of 102 data sets are considered for training.
2) A testing dataset. This is required to estimate the model performance. In this study, the remaining 12 out of 102 are used as the testing data set.
3.2 Establishment of SVMs model
Rock fragmentation is considered a dynamic instability. Particle size distribution of a muck pile is controlled by three main blasting parameters: blast design parameters, explosive parameters and properties of the rock mass [5, 14, 32-34]. To estimate fragmentation, five main blast design parameters are used in the developed SVMs models. They are the burden (B), spacing (S), bench height (H), stemming (T) and hole diameter (D). All these parameters are controllable. Figure 3 shows most of the blast design parameters used in a bench blast [5, 35]. The ratio of bench height to drilled burden (H/B), ratio of spacing to burden (S/B), ratio of burden to hole diameter (B/D) and ratio of stemming to burden (T/B) are the blast design parameters used. The powder factor (Pf) is considered an explosive parameter. Thus 7 parameters were used to establish the fragmentation prediction models based on SVR incorporating the blast design parameters, modulus of elasticity (E) and in-situ block size (XB) [5, 14]. Table 2 indicates the relevant parameters as well as their respective symbols used to develop fragmentation prediction models with their range, mean and standard deviation, respectively.
The boxplot of the original data set is given in Fig. 4. For the most of the data groups, the median is not in the centre of the box, which indicates that the distribution of the most of the data groups is not symmetric (Fig. 4). In addition, dependent variables of H/B, XB and E do not have any outliers whereas S/B, B/D, T/B, Pf and X50 have at least one outlier (Fig. 4).
LI [25], CHANG and LIN [26] developed an Libsvm toolbox for SVR modeling in Matlab application. This toolbox is used here for the application of SVR in predicting X50 of rock fragmentation due to blasting. The input–output data are scaled to lie between 0 and 1 by using the following equation [18-24].
xnorm=(x-xmin)/(xmax-xmin) (9)

Fig. 2 Scatter plot matrix of original data set
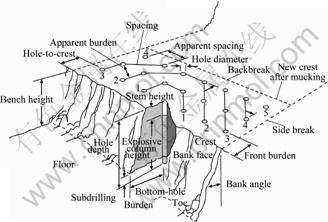
Fig. 3 Geometric blast design parameters terminology [5, 35]
Table 2 Descriptive statistics of input and output parameters with their range, mean and standard deviation for SVR modeling

Fig. 4 Boxplot of original data set
where xnorm is the normalized value, x is the actual value, xmax is the maximum value, and xmin is the minimum value.
The engineering data in Refs. [5,14] are introduced to show how the SVR method is applied in practice. In the present study, the above SVR model is used for prediction of X50 resulting from rock blast fragmentation. In SVR, each of the input variables (S/B, H/B, B/D, T/B, Pf, XB, E) is first normalized to its respective maximum values [18-24]. The output variable X50 is also normalized with respect to the maximum mean particle size value. 90 sets of samples are selected as the training samples of SVR model (listed in Table 1) [5,14]. SVR model is established using the SVR theory discussed above.
3.3 Testing and validation of SVMs
When applying SVR, the goodness of fit is determined by the penalty factor C. A higher C value means more support vectors; but a too high C value could drop the regression performance, so it is helpful for the regression analysis to choose a suitable penalty factor. Insensitive parameter g is an interpretation of the regression curve accuracy. A greater g value means the lower generalization performance of the regression curve. Libsvm [25,26] provides a parameter selection tool using the RBF kernel: cross validation via parallel GSM [22,23,27]. While cross validation is available for both SVC and SVR. For the grid search, currently we support only C-SVC with two parameters C and g. They can be easily modified for other kernels such as linear and polynomial, or for SVR. In this study, the free parameters of SVR are selected followed a 5-fold cross-validation experiment to control generalization capability of SVMs, and the RBF kernel is used as the kernel function of the SVR because it tends to give better performance. Gaussian kernel function is adopted as the kernel function of the samples training, obtaining the best parameters by GSM [25]. Figure 5 shows an example of the GSM result, where the x-axis and y-axis are log2C and log2g, respectively. The z-axis is the 5-fold average performance. The findings of this experiment are that SVR is quite robust against parameter selections. In the present study, training and testing of SVR are carried out by using Matlab 7.0 program [34].

Fig. 5 MSE values for different combinations of log2C and log2g
The result of the SVR parameter selection by GSM is shown in Fig. 5 (3D view). When C is 5.657, g =1 and the average value of MSE is 0. 0.0374. 90 sets of training sample data are back evaluated one by one using the SVMs model of rock fragmentation and compared with the actual situation. The comparison of results of X50 estimation for training data are shown in Fig. 6. The regression mean-square error of the study sample is 0.0144, and the square correlation coefficient is 0.9263. From Fig. 6, SVR has good performance for regression forecast, which proves that the model has stable and reliable prediction ability. Therefore, the SVMs model is feasible and effective for rock fragmentation forecasting and can be put into use. As shown in Fig. 6, the prediction curve obtained by SVR training sample fits good.

Fig. 6 Actual vs prediction values using SVR with training data
Here is used to validate the predictive models based on the comparison of the predicted and measured (real) values. 12 testing samples (listed in Table 3) are validated by the SVR model. The results are identical with the actual mean particle size and the accuracy of this rock fragmentation regression model is good.
4 Results and discussion
Many traditional methods for mean particle size prediction of rock blast fragmentation have been presented in the literature. Among these, three are chosen for the purpose of assessing the relative performance of the SVMs model. These include the Kuznetsov method [5,14], MVRA method [5,14] and ANN approach [5]. The comparison of the results of X50 estimation obtained using the SVR, ANN and the two traditional methods for the testing dataset are presented in Table 4.
In estimating the SVR model prediction performance, the results of SVR models are compared with that of Kuznetsov method, MRVR and ANN method. Computing indexes, such as correlation coefficient (R2), mean absolute error (MAE) and root mean square error (RMSE), can be used to evaluate the prediction accuracy of SVR and other prediction models [18-24]. These indexes can be calculated by the following equations:
 (10)
(10)
 (11)
(11)
 (12)
(12)
where Ti, Oi and n represent the measured output, the predicted output and the number of input-output data pairs, respectively.
Table 3 Summary of testing data for rock fragmentation analysis of some projects around the world [5, 14]

Table 4 Comparison of results of X50 estimation for testing sets by different methods

In Table 5, R2, MAE and RMSE between the observed and predicted values of SVR model are found to be 0.962, 0.066 and 0.006, respectively for testing data. From Table 5, the same for the predicted values by using Kuznetsov method [5,14] are found to be 0.614, 0.344 and 0.025 respectively, the corresponding values by MRVR method [5,14] are 0.815, 0.170 and 0.017, whereas the corresponding values by ANN method [5] are 0.941, 0.107 and 0.009. So, it can be seen that the SVR method has very high R2 value (0.962) and exhibits good correlation between predicted X50 and actual X50. In Fig. 7 the comparison of the predicted X50 using Kuznetsov’s method, MVRA, ANN and SVR methods and their deviation from the observed one is shown. It is observed that the SVR predicted values are less scattered and are close to the observed values signified by its closeness to the line of equality.
Table 5 Performance indexes of R2, RMSE and MAE

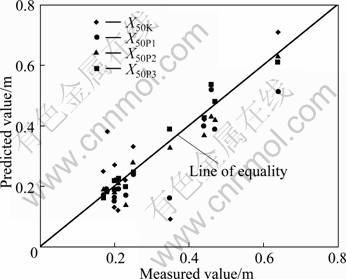
Fig. 7 Comparison of predicted mean particle size by different methods with measured values
Table 5 shows that the SVMs method performs better than the traditional methods. It can be concluded that the SVR model can be applied to forecasting the rock fragmentation in opencast mines regression with high accuracy.
The data are also presented as boxplots in Fig. 8. By comparing the size of the boxes for each predictive model with the observed data, clearly the predictive model based on SVR almost duplicates the observed values, indicating that this is the best method for predicting X50.

Fig. 8 Boxplot of testing data set by different methods with measured values
The above-mentioned comparisons indicate that all four models are competitive with each other for X50 prediction in rock fragmentation, but the performance of the SVMs is relatively superior to the others. Moreover, the SVMs have some added advantages, which come from the specific formulation of a (convex) objective function with constraints. This function is solved using Lagrange multipliers and has some inherent advantages and characteristics [18-24]: 1) a global optimal solution exists that will be found; 2) the result is a general solution avoiding overtraining; 3) the solution is sparse and only a limited set of training points contribute to this solution; and 4) nonlinear solutions can be calculated efficiently due to the usage of inner products.
In particular, the use of SRM principle in defining cost function provides more generalization capacity with the SVMs compared with the ANN, which uses the ERM principle. The number of free parameters is another advantage of using the SVMs. In the case of RBF, there are only three parameters in the SVMs, namely, C, g, and ε, whereas in the ANN, there are a large number of controlling parameters, including the number of hidden layers, the number of hidden nodes, learning rate, momentum term, the number of training epochs, transfer functions, and weight initialization methods. Obtaining an optimal combination of these parameters is a difficult task as well. Another major advantage of the SVMs is its optimization algorithm, which includes solving a linearly constrained quadratic programming function leading to a unique, optimal, and global solution compared with the ANN. Moreover, there is a high potential for further improvement of the SVMs performance [19-24]. While in the MVRA, capturing of high non-linearity incorporating many parameters is a difficult task with MVRA. Because the blast fragmentation distribution depends on many parameters, and the process is highly complex due to the heterogeneity and anisotropy of a discontinuous rock mass system, it is impossible to derive an equation for fragmentation distribution purely from theoretical and mechanistic reasoning.
5 Conclusions
1) A new method is presented to forecast the rock fragmentation due to bench blasting by using the SVMs model. The factors including blast design parameters, explosive parameters, modulus of elasticity and in-situ block size are taken into account to build a forecast SVR model. A SVR model is obtained through training 90 sets of practical measuring samples and 12 new data. The result indicates that SVR method is scientific and feasible with high accuracy, which provides a new way for the regression prediction of rock fragmentation.
2) The proposed method shows promising results and proves to be competitive with the widely used ANN and conventional Kuznetsov method, MVRA model.
3) The SVR theory has been successfully demonstrated for forecasting X50 resulting from rock blast fragmentation and some problems should be researched in the future. One direction of future work would be enlarging the blast databases that will be used to develop fragmentation prediction models presented in this study, and another possible direction of future work would be considering additional rock parameters of the rock mass that would be subjected to blasting if information on such metrics is available.
References
[1] JIMENO C L, JIMENO E L, CARCEDO F J A. Drilling and blasting of rocks [M]. Rotterdam: Taylor & Francis US, 1995.
[2] HAMDI E, DU MOUZA J, FLEURISSON J A. Evaluation of the part of blasting energy used for rock mass fragmentation [J]. Fragblast: The International Journal for Blasting and Fragmentation, 2001, 5(3): 180-193.
[3] ALER J, DU MOUZA J, ARNOULD M. Measurement of the fragmentation efficiency of rock mass blasting and its mining applications [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1996, 33(2): 125-139.
[4] MONJEZI M, AMIRI H, FARROKHI A, GOSHTASBI K. Prediction of rock fragmentation due to blasting in Sarcheshmeh copper mine using artificial neural networks [J]. Geotechnical and Geological Engineering, 2010, 28: 423-430.
[5] KULATILAKE P H S W, WU Q, HUDAVERDI T, KUZU C. Mean particle size prediction in rock blast fragmentation using neural networks [J]. Engineering Geology, 2010, 114(3-4): 298-311.
[6] KUZNETSOV V M. The mean diameter of the fragments formed by blasting rock [J]. Soviet Mining Science, 1973, 9(2): 144-148.
[7] CUNNINGHAM C. The Kuz–Ram model for prediction of fragmentation from blasting [C]//HOLMBERG R, RUSTAN A. Transactions of the First International Symposium on Rock Fragmentation by Blasting (Vol. 2). Lülea, Sweden: Lülea University of Technology, 1983: 439-453.
[8] ROSIN R, RAMMLER E. Laws governing the fineness of coal [J]. J Inst Fuels, 1933, 7: 29-36.
[9] GHEIBIE S, AGHABABAEI H, HOSEINIE S H, POURRAHIMIAN Y. Modified Kuz-Ram fragmentation model and its use at the sungun copper mine [J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(6): 967-973.
[10] OZKAHRAMAN H T. Fragmentation assessment and design of blast pattern at Goltas Limestone Quarry, Turkey [J]. International Journal of Rock Mechanics & Mining Sciences, 2006, 43: 628-633.
[11] SIDDIQUI F I, ALI SHAH S M, BEHA M Y. Measurement of size distribution of blasted rock using digital image processing [J]. Engineering Sciences, 2009, 20(2): 81-93.
[12] SUDHAKAR J, ADHIKARI G R, GUPTA R N. Comparison of fragmentation measurements by photographic and image analysis techniques [J]. Rock Mechanics and Rock Engineering, 2006, 39(2): 159-168.
[13] ALER J, DU MOUZA J, ARNOULD M. Evaluation of blast fragmentation efficiency and its prediction by multivaraiate analysis procedures [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1996, 33(2): 189-196.
[14] HUDAVERDI T, KULATILAKE P H S W, KUZU C. Prediction of blast fragmentation using multivariate analysis procedures [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35(12): 1318-1333.
[15] MARIO A M, FRANCESCO F. Monte Carlo simulation as a tool to predict blasting fragmentation based on the Kuz–Ram model [J]. Computers & Geosciences, 2006, 32: 352-359.
[16] MONJEZI M, REZAEI M, VARJANI A Y. Prediction of rock fragmentation due to blasting in Gol-E-Gohar iron mine using fuzzy logic [J]. International Journal of Rock Mechanics & Mining Sciences, 2009, 46: 1273-1280.
[17] VAPNIK V. The nature of statistical learning theory [M]. New York: Springer Verlag, 1995.
[18] FENG X T, ZHAO H, LI S. Modeling non-linear displacement time series of geomaterials using evolutionary support vector machines [J]. International Journal of Rock Mechanics & Mining Sciences, 2004, 41(7): 1087-1107.
[19] GOPALAKRISHNAN K, KIM S. Support vector machines approach to HMA stiffness prediction [J]. Journal of Engineering Mechanics (ASCE), 2011, 137(2): 138-146.
[20] THISSEN U, Van BRAKEL R, de WEIJER A P, MELSSEN W J, BUYDENS L M C. Using support vector machines for time series prediction [J]. Chemometrics and Intelligent Laboratory Systems, 2003, 69: 35-49.
[21] SAMUI P, SITHARAM T G, KURUP P U. OCR prediction using support vector machine based on piezocone data [J]. Journal of Geotechnical and Geoenvironmental Engineering (ASCE), 2008, 134(6): 894-898.
[22] ZHOU Jian, LI Xi-bing, SHI Xiu-zhi. Long-term prediction model of rock burst in underground openings using heuristic algorithms and support vector machines [J]. Safety Science, 2012, 50(4): 629-644.
[23] ZHOU Jian, LI Xi-bing, SHI Xiu-zhi, WEI Wei, WU Bang-biao. Predicting pillar stability for underground mine using Fisher discriminant analysis and SVM methods [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(12): 2734-2743.
[24] GUNN S R. Support vector machines for classification and regression [R]. Technical report, Image speech and intelligent systems research group, University of Southampton, UK, 1997. http://www.isis. ecs.soton.ac.uk/isystems/kernel/.
[25] LI Y. LIBSVM-faruto ultimate version: A toolbox with implements for support vector machines based on Libsvm [EB/OL]. http://www. ilovematlab.cn.
[26] CHANG C C, LIN C J. LIBSVM: A library for support vector machines [EB/OL]. http://www.csie. ntu. edu. tw/ ~cjlin/libsvm.
[27] LIN H T, HUANG T K. Grid parameter search for regression [EB/OL]. http://www.csie.ntu.edu.tw /~cjlin/libsvmtools/.
[28] HUDAVERDI T. The investigation of the optimum parameters in large scale blasting at KBI black sea copper works-murgul open-pit mine [D]. Istanbul Technical University, 2004: 45-67 (in Turkish).
[29] OUCHTERLONY F, NIKLASSON B, ABRAHAMSSON S. Fragmentation monitoring of production blasts at Mrica [C]//MCKENZIE C. International Symposium on Rock Fragmentation by Blasting, FragBlast 3. Brisbane, Australia, 1990: 283-289.
[30] OZCELIK Y. Effect of discontinuities on fragment size distribution in open-pit blasting-a case study [J]. Transactions of the Institution of Mining and Metallurgy, 1998, 107: 146-150.
[31] JHANWAR J C, JETHWA J L, REDDY A H. Influence of air-deck blasting on fragmentation in jointed rocks in an open-pit manganese mine [J]. Engineering Geology, 2000, 57(1-2): 13-29.
[32] THORNTON D, KANCHIBOTLA S S, BRUNTON I. Modelling the impact of rock mass and blast design variation on blast fragmentation [J]. Fragblast, 2002, 6(2): 169-183.
[33] PAL ROY P. Breakage assessment through cluster analysis of joint set orientations of exposed benches of opencast mines [J]. Geotechnical and Geological Engineering, 1995, 13: 79-92.
[34] HAMDI E, MOUZA J D. A methodology for rock mass characterization and classification to improve blast results [J]. International Journal of Rock Mechanics & Mining Sciences, 2005, 42(2): 177-194.
[35] ASH R L. The mechanics of the rock breakage (Part 1) [J]. Pit and Quarry, 1963, 56(2): 98-100.
台阶爆破岩石破碎平均粒径预测的支持向量机方法
史秀志1, 周 健1, 吴帮标1, 2, 黄 丹1, 魏 威1
1. 中南大学 资源与安全工程学院,长沙 410083;
2. 多伦多大学 土木工程系,加拿大 多伦多,M4Y 1R5
摘 要:针对传统的岩石台阶爆破破碎评估问题,运用统计学理论,建立预测不同矿山岩石爆破破碎后的平均粒径 (X50)的支持向量机 (SVMs)回归模型。爆破参数包括爆破设计参数、炸药参数、弹性模量及现场块度大小。SVMs模型选用7个参量作为预测岩石爆破破碎的平均粒径X50输入自变量:台阶高度与钻孔荷载比(H/B),间距与荷载比(S/B),荷载与孔径比(B/D),炮泥与荷载比(T/B),粉因数(PF),弹性模量(E)和现场块度大小(XB)。利用世界各地不同矿山和岩层测量的90组数据来训练和测试SVMs模型,其他12组爆破数据来验证该模型的有效性,并将SVR的预测结果与人工神经网络(ANN)、多元回归分析(MVRA)、传统的 Kuznetsov 方法及X50实测值进行比较。该方法显现出很好的效果,其预测精度是可以接受的。
关键词:岩石破碎;爆破;平均粒径;支持向量机;预测
(Edited by YUAN Sai-qian)
Foundation item: Project (2006BAB02A02) supported by the National Key Technology R&D Program during the 11th Five-year Plan Period of China; Project (CX2011B119) supported by the Graduated Students' Research and Innovation Fund of Hunan Province, China; Project (2009ssxt230) supported by the Central South University Innovation Fund, China
Corresponding author: SHI Xiu-zhi; Tel: +86-13974801752; E-mail: shixiuzhi@263.net
DOI: 10.1016/S1003-6326(11)61195-3