Article ID: 1003-6326(2005)05-1096-07
Effect of process variables on grain growth in simulating solidification microstructure of Ti-45%Al alloy ingot by stochastic model
WU Shi-ping(吴士平), LIU Dong-rong(刘东戎),
GUO Jing-jie(郭景杰), FU Heng-zhi(傅恒志)
(School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China)
Abstract: A comprehensive stochastic model for simulating microstructure formation of Ti-45%Al(mole fraction) alloy ingot during solidification process was developed, based on a finite differential method(FDM) for macroscopic heat flow calculation and a cellular automaton(CA) technique for microscopic modeling of nucleation and growth. The formation of a shrinkage cavity at the top of ingot was taken into account. The effects of process variables such as pouring temperature and mold-preheated temperature on the microstructure formation were investigated. The calculated results indicate that the columnar zone is expanded with increasing pouring temperature in the nonlinear way and the volume fraction of equiaxed zone only slightly varies with the mold-preheated temperature.
Key words: Ti-45%Al alloy; solidification grain structure; process variable; cellular automaton CLC number: TG27
Document code: A
1 INTRODUCTION
Ti-Al alloy exhibits a remarkable potential for structural applications in aerospace and automotive industries at high temperatures. During the last decade, research and development of this alloy were focused on a better understanding of the microstructure formation. Thus, the prediction of microstructure formation is important for the control of final grain size, morphology, and the quality of cast products[1]. In recent years, computer simulation has been used for this purpose[1-17]. Cho et al[14] have studied the microstructural formation and columnar-to-equiaxed transition(CET) in squeeze casting of Al-4.5%Cu(mass fraction) alloys. Lee et al[15, 16] have predicted the columnar dendritic growth in a flowing melt and solidification grain structure formation in centrifugal casting of Al-Si alloy. Gandin et al[17] have developed a three-dimensional CA model for the prediction of dendritic grain structures of a pigtail grain selector and aluminum-silicon rods. These computer-based predictive models for linking processing conditions to microstructures of processed materials, can describe the major phenomena that control the process, and are becoming powerful tools in studying grain structure formation and evolution involving nucleation and growth of grains[7]. However, the literature on the Ti-Al alloy is rather scarce.
Motivated by this situation, in the present study, a stochastic model for simulating microstructure formation of Ti-45%Al(mole fraction) alloy ingot is developed. The formation of a shrinkage cavity at the top of ingot is considered. The effects of process variables such as pouring temperature and mold-preheated temperature are investigated. The calculated results are analyzed theoretically.
2 COMPUTING MODEL
2.1 Governing equations
First, the following simplifying assumptions are made in developing the model: 1) the effect of convection in the liquid pool is not taken into account; 2) the heat transfer is controlled by the thermal properties of this alloy and any influence of microstructure on the heat transfer is neglected and 3) all thermal and physical properties are assumed to be constant.
The thermal transfer equation is
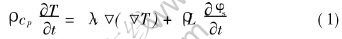
where ρ is the density, cp is the specific heat capacity, λl is the thermal conductivity, L is the latent heat, and φs is the solid fraction.
The solute diffusion equation in liquid is

where Dl is the liquid diffusion coefficient and Cl is the liquid concentration. The solute diffusion in the solid is not considered.
2.2 Nucleation model
The Gaussian law is used in the continuous nucleation model:
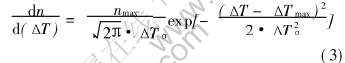
where n is the nuclei density,nmax is the maximum nuclei density, ΔTσ and ΔTmax are the standard deviation and the mean nucleation undercooling, respectively.
2.3 Growth model
For the case of columnar dendritic solidification, the Kurz-Giovanola-Trivedi(KGT) model[18] is used to calculate the growth rate:
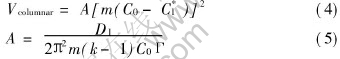
where Γ is the Gibbs-Thomson coefficient, m is the liquidus slope and A is the growth coefficient. For the equiaxed dendritic solidification, the model developed by Nastac et al[19] is applied. Thus, the growth velocity of the tip is described by
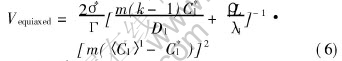
where 〈Cl〉l is the volume average extradendritic liquid concentration and σ*=1/(4π2).
2.4 Columnar-to-equiaxed transition(CET) model
The Hunt-CET model[20] is
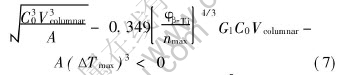
where φβ -Ti is the solid fraction of β-Ti at the peritectic reaction temperature, Gl is the temperature gradient and nmax is not a constant value, but a function of pouring temperature. For the solidification of Ti-Al alloy ingot, it is assumed that only when Eqn.(7) is not satisfied and bulk liquid is at an almost uniform temperature can CET occur[21].
3 RESULTS AND DISCUSSION
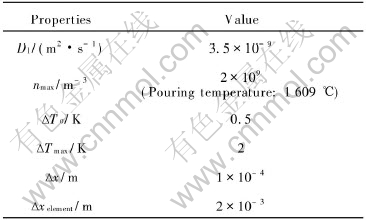
The present stochastic model is applied to simulate the grain structure formation and evolution of Ti-45%Al alloy ingot. The schematic of two-dimensional ingot vertical section is shown in Fig.1, where all dimensions are in millimeters. The employed thermophysical properties of casting and mold materials are summarized in Table 1. Other parameters used for simulation are listed in Table 2.
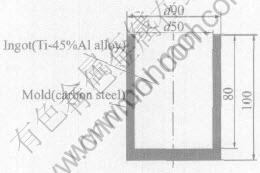
Fig.1 Schematic illustration of ingot and mold (unit: mm)
Table 1 Corresponding thermophysical data[22]
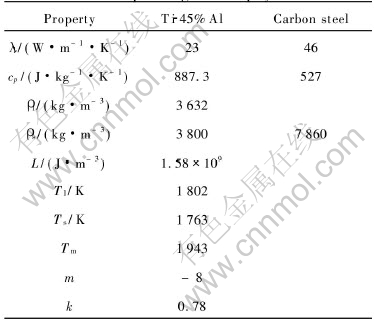
Table 2 Parameters used for simulation
3.1 Validation of developed model
To verify the results computed from the developed model, one Ti-45%Al alloy ingot with 100mm in diameter and 280mm in length was melted in the ISM apparatus[21] and then solidified in the metal mold. The casting conditions were pouring temperature of 1609℃ and mold temperature of 25℃. The resultant ingot was sectioned vertically on a mid-plane and the surface was polished and etched.
Fig.2 shows both the simulated results and the experimental one. Here, it should be pointed out that for the experimental sample, the upper part has been cut out due to the formation of a shrinkage cavity. While slight discrepancy observed near the bottom of the ingot may be attributed to the fact that sedimentation of equiaxed grains in the melt is not taken into account in the model, the simulated microstructure still matches well with the experimental one, confirming the reliability of the model used in the present work.
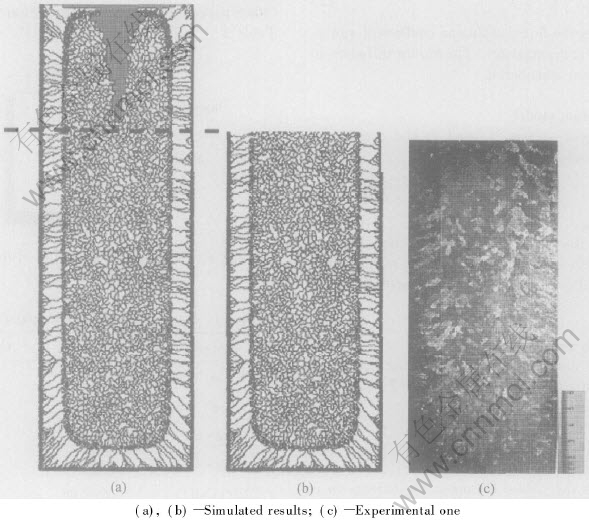
Fig.2 Comparison of simulated microstructures and experimental result
3.2 Effect of pouring temperature on microstructure formation
The pouring temperature is an important parameter that affects the solidification grain structures. Fig.3 indicates the simulated microstructure formation and evolution of Ti-45%Al alloy ingot with mold temperature of 25℃ and pouring temperatures of: (a) 1650℃, (b) 1600℃, (c) 1550℃ and (d) 1530℃. As shown in this figure, all the ingots exhibit columnar structures growing perpendicular to the chill surface, followed by equiaxed grains up to the center of the ingot, and the volume fractions of columnar zone and equiaxed zone are affected by the superheat. An increase in pouring temperature is found to promote the occurrence of columnar growth further. It is mainly due to that the higher temperature gradient at the columnar grain front minimizes the constitutional undercooling zone, which may delay the columnar-to-equiaxed transition.
A CET map for the Ti-45%Al alloy with different pouring temperatures is shown in Fig.4. Transition lines (predicted by the Hunt-model) are shown for pouring temperatures of 1650℃ and 1550℃. It can be noted that with increasing superheat, the transition line moves from the right to the left, which means that the CET may not easily occur. This is attributed mainly to the fact that a higher temperature gradient is built at the solidification front and heterogeneous nucleation sites in the bulk liquid decrease with increasing pouring temperature.
The solidification paths for the Ti-45%Al alloy are superimposed on the map. The calculated growth velocity and temperature gradient combinations at columnar front position Zcol are indicated on the pathline as squares and circles. At the initial stage of solidification, although the growth velocities are larger near the chill surface, the dominant factor in determining CET is the temperature gradient rather than the velocity. As a result of this, the columnar growth is favored. As solidification proceeds, temperature gradient begins to flatten, causing the increase of the amount of undercooling in the bulk liquid. Hence, the equiaxed growth may take place ahead of the columnar front and the CET occurs. It can be noted that the CET occurs in the low-G regime of the map, where the transition lines are horizontal. It can be concluded that the decrease in pouring temperature transforms into an equivalent decrease in the temperature gradient and in the time for temperature gradient flattening. Both factors facilitate the CET.

Fig.3 Simulated solidification microstructures of Ti-45%Al alloy ingot at
different solidification times for various pouring temperatures
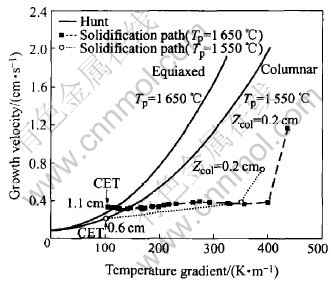
Fig.4 CET map for Ti-45%Al alloy ingot
The dependence of mean grain size on pouring temperature is shown in Fig.5. It is obvious that solidification with a higher pouring temperature leads to a larger columnar zone and a coarser equiaxed grain structure. However, it can be noted that as the pouring temperature increases, the mean grain size increases in a nonlinear way.
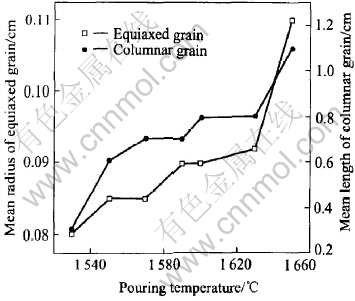
Fig.5 Dependence of mean grain size on pouring temperature
3.3 Effect of mold temperature on grain structure formation
With pouring temperature of 1650℃, the mold is preheated to different temperatures, ranging from 50℃ to 800℃. Fig.6 shows the heat flow from the ingot to the mold as a function of time for the various mold temperatures. In both cases, a rapid rise in the heat flow is seen as the molten melt enters the mold, as well as the subsequent drop due to the air gap formation. The lower the temperature of the mold before casting, the larger the maximum heat flow. This means that for the mold with higher preheated temperature, its cooling capacity may be reduced, which may affect the following solidification processes, i.e. solidification time and cooling rate.
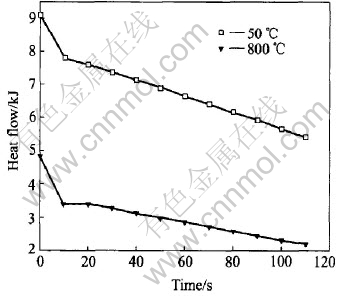
Fig.6 Heat flow as function of time for various mold-preheated temperatures
The connection between the solidification time and the solidified fraction of ingot is illustrated in Fig.7. A prominent feature is the fact that the solidification time of ingots for the initial mold temperatures of 50℃ and 300℃ is nearly equal. This means that altering the initial mold temperature within a special range does not have obvious effect on the solidification processes. It is mainly attributed to the fact that heat lost in the ingot proceeds according to two mechanisms[23]: close to the metal/mold interface, heat conduction into the mold and cooling by radiation after the air gap formation. At the initial solidification stage, the former plays an important role and as the solidification proceeds, the latter is the dominant mechanism. Thus, although the mold is preheated to some extent, a high temperature gradient still exists at the metal/mold interface which acts as the strong driving force for heat transfer, outweighing the reduction in the cooling capacity of mold. When cast at a mold temperature higher than 300℃, the higher the preheated temperature, the longer the solidification time.
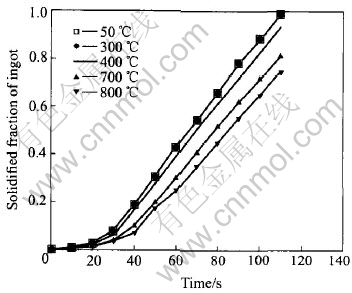
Fig.7 Solidified fraction of ingot as function of time for different mold-preheated temperatures
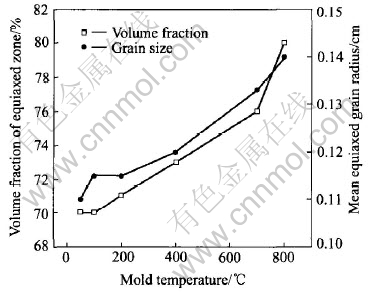
Fig.8 Volume fraction of equiaxed zone and mean equiaxed grain radius as function of mold temperature
The mean equiaxed grain radius and the volume fraction of equiaxed zone are plotted as a function of mold temperature in Fig.8. The mean equiaxed grain sizes are finer for the lower mold preheated temperature. However, it can be noted that there is only slight variation in the volume fraction of equiaxed zone. This can be explained by the examination of the temperature distribution. The temperature distributions at different time for mold temperatures of 50℃, 700℃ and 800℃ are plotted in Fig.9. For the three cases, at t=40s, the temperature profile is located entirely under the liquidus temperature for the first time. In Ref.[21], it has been indicated that only when liquid is at an almost uniform temperature can equiaxed zone be formed. Furthermore, from Fig.7, it is clear that at t=40s, no great variation is found in the solidified volume. This is why the volume fraction of the equiaxed zone is closely similar.
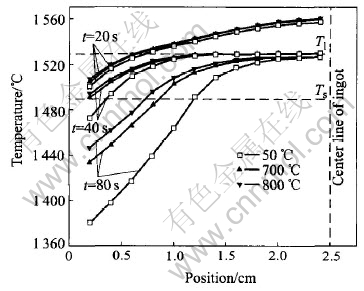
Fig.9 Temperature distributions at different times for various mold-preheated temperatures
4 CONCLUSIONS
1) A comprehensive stochastic model based on a FDM method for macroscopic modeling of heat transfer and a CA technique for microscopic modeling of nucleation and growth, is developed for the simulation of grain structure formation of Ti-45%Al alloy ingot during solidification processes.
2) When the simulated microstructure and the experimental result are compared, good consistency is observed. The developed model is then validated. The effects of process variables such as pouring temperature and mold-preheated temperature on the grain structure formation are examined. The higher pouring temperature leads to a coarser equiaxed grain structure and a larger columnar zone. With increasing superheat, the mean grain size increases in a nonlinear way. Higher mold preheated temperature also produces a coarser grain structure, however, it has minor influence on the variation of volume fraction of equiaxed zone.
REFERENCES
[1]Ho K S, Kuo J H, Hwang W S. Grain morphology simulation for precision casting of Rene 77 alloy and its experimental verification [J]. AFS Transitions, 2003, 111: 1113-1125.
[2]Lipton J, Glicksman M E, Kurz W. Equiaxed dendrite growth in alloys at small supercooling [J]. Metall Trans A, 1987, 18(2): 341-345.
[3]Wang C Y, Beckermann C. A multiphase solute diffusion model for dendritic alloy solidification [J]. Metall Trans A , 1993, 24(12): 2787-2802.
[4]Martorano M A, Beckermann C. A solutal interaction mechanism for the columnar-to-equiaxed transition in alloy solidification [J]. Metall Trans A, 2003, 34(8): 1657-1673.
[5]Spittle J A, Brown S G R. Dynamic simulation of crystal growth by Monte Carlo method(Ⅱ)—Ingot microstructures [J]. Acta Mater, 1992, 40(12): 3369-3379.
[6]Rappaz M, Gandin C A. Probabilistic modelling of microstructure formation in solidification processes [J]. Acta Mater, 1993, 41(2): 345-360.
[7]Gandin C A, Charbon C H, Rappaz M. Stochastic modeling of solidification grain structure [J]. ISIJ Int, 1995, 35(6): 651-657.
[8]WANG Tong-min, JIN Jun-ze, ZHENG Xian-shu, et al. A novel simulation method for the prediction of dendritic grain structures in solidification [J]. Int J Cast Metals Res, 2002, 15(5): 231-236.
[9]XU Qing-yan, FENG Wei-ming, LIU Bai-cheng. Stochastic modeling of dendritic microstructure of aluminum alloy [J]. Int J Cast Metals Res, 2002, 15(5): 225-230.
[10]Kim J M, Zhu M F, Hong C P. Evolution of primary phase in solidification of Al-Si alloys [J]. Int J Cast Metals Res, 2002, 15(5): 285-289.
[11]Zhu M F, Nishido S, Hong C P. Modeling of eutectic structure formation by a modified cellular automaton model [J]. Int J Cast Metals Res, 2002, 15(5): 273-278.
[12]ZHANG L, WANG Y M, ZHANG C B, et al. A cellular automaton model of the transformation from austenite to ferrite in low carbon steels [J]. Modelling Simul Mater Sci Eng, 2003(11): 791-802.
[13]Lee K Y, Hong C P. Stochastic modeling of solidification grain structures of Al-Cu crystalline ribbons in planar flow casting [J]. ISIJ Int, 1997, 37(1): 38-46.
[14]Cho I S, Hong C P. Modeling of microstructural evolution in squeeze casting of an Al-4.5wt%Cu alloy [J]. ISIJ Int, 1997, 37(11): 1098-1106.
[15]Lee S Y, Lee S M, Hong C P. Numerical modeling of deflected columnar dendritic grains solidified in a flowing melt and its experimental verification [J]. ISIJ Int, 2000, 40(1): 48-57.
[16]Lee S Y, Lee S M, Hong C P. Numerical simulation of microstructure evolution of Al alloys in centrifugal casting [J]. ISIJ Int, 2001, 41(7): 738-747.
[17]Gandin C A, Desbiolles J L, Rappaz M, et al. A three-dimensional cellular automaton-finite element model for the prediction of solidification grain structures [J]. Metall Trans A, 1999, 30(12): 3153-3165.
[18]Kurz W, Giovanola B, Trivedi R. Theory of microstructural development during rapid solidification [J]. Acta Mater, 1986, 34(5): 823-830.
[19]Nastac L, Stefanescu D M. Macrotransport-solidification kinetics modeling of equiaxed dendritic growth(Part Ⅰ): Model development and discussion [J]. Metall Trans A, 1996, 27(12): 4061-4074.
[20]Hunt J D. Steady state columnar and equiaxed growth of dendrites and eutectic [J]. Mater Sci Eng, 1984, 65: 75-83.
[21]ZHAO Jin-qian. The Melting and Casting Technology of Large-size TiAl-based Alloy Ingot [D]. Harbin: Harbin Institute of Technology, 2004. 27-30.
[22]SU Yan-qing, LIU Chang, LI Xin-zhong, et al. Microstructure selection during the directionally peritectic solidification of Ti-Al binary system [J]. Intermetallics, 2005, 13(3-4): 267-274.
[23]Avishei A, Bamberger M. Relation between cooling rates and microstructures in gravity-die-cast AZ91D disks [J]. Metall Trans B, 1999, 30(8): 723-729.
Foundation item: Project(50395102) supported by the National Natural Science Foundation of China
Received date: 2004-12-22; Accepted date: 2005-04-04
Correspondence: WU Shi-ping, Associated Professor, PhD; Tel: +86-451-86418815; E-mail: spwu@hit.edu.cn
(Edited by YUAN Sai-qian)