
Thermodynamics of solubility of Cu2(OH)2CO3in ammonia-ammonium chloride-ethylenediamine(En)-water system
LIU Wei(刘 维), TANG Mo-tang(唐谟堂), TANG Chao-bo(唐朝波),
HE Jing(何 静), YANG Sheng-hai(杨声海), YANG Jian-guang(杨建广)
School of Metallurgical Science and Engineering, Central South University, Changsha 410083, China
Received 6 July 2009; accepted 25 December 2009
Abstract: In order to decrease the evaporating rate of ammonia and increase the solubility of copper in the solution, ethylenediamine was added into the ammonia-ammonium chloride system to leach the copper-containing oxide ores. The thermodynamic model was constructed and the solubility of malachite Cu2(OH)2CO3 in the ammonia-ammonium chloride-ethylenediamine(En)-water system was calculated using the exponential computation method based on both mass balance and charge balance. It is found that the solubility of copper can be increased and the free ammonia concentration can be decreased by submitting partial ammonia with ethylenediamine. The lower free ammonia concentration in the solution is a guarantee to the lower evaporating rate of ammonia. The conditions of malachite Cu2(OH)2CO3 converting to atacamite Cu(OH)1.5Cl0.5 were also studied. A group of experiments were designed to validate the veracity of the results of the thermodynamic calculation. It is found that the thermodynamic model is reliable and it can guide the leaching process.
Key words: thermodynamics; solubility; malachite; ammonia; ammonium chloride; ethylenediamine(En)
1 Introduction
Ammonia is a good selective reagent for copper extraction. Many researches have been focused on the leaching of copper oxide ore with ammonic solution especially when the gangue is composed of carbonates [1-4].
The thermodynamic and kinetic characteristics of dissolving of copper oxide ore in ammonic solution have been widely studied[5-7]. However, the volatilization of ammonia during operation always makes the working environment very terrible. In order to overcome this shortcoming, the ethylenediamine(En), which has a higher boiling point, is used to substitute partial ammonia[8]. RAMDANE[9], SERDAR and FIONA[10] investigated the φ-pH diagrams of the Cu-En-H2O system. But the dissolving characteristics of the copper oxide ores in ammonia-ammonium chloride- ethylenediamine(En)-water solution was not yet illustrated clearly. In this work, an attempt is made to study the solubility of Cu2(OH)2CO3 in the ammonia- ammonium chloride-ethylenediamine(En) solution. The calculations, based on both mass balance and charge balance equations, are made to express equilibrium relations between solid phase and associated solution in terms of total concentrations of the actual lixiviants ammonia, ammonium chloride and ethylenediamine(En). Furthermore, the solution composition for keeping Cu2(OH)2CO3 stable is also established.
2 Thermodynamic model
2.1 Data selection
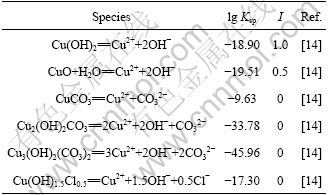
Considering that the activity of each ion is approximated by its mole concentration in this work and the concentration of each ion is in relatively high level, the data determined at the highest ionic intensity are selected from the literature. The stability constants are listed in Tables 1-3.
Table 1 Cumulative formation constants of copper complexes at 298 K
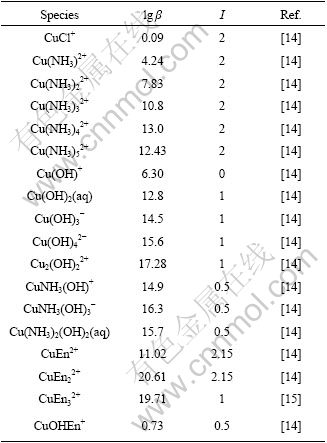
Table 2 Constants of addition proton at 298 K
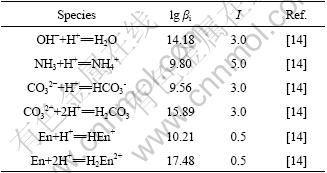
Table 3 Solubility-product constants (Ksp)
2.2 Calculation method
As mentioned by TANG et al[11-13] in their studies, all the concentrations of ions in the solution can be expressed as [X]=exp(a+bpH+cφ+eln[L1]+fln[L2]…), where a, b, c, e and f are coefficients; φ is the value of potential which is only needed when redox reactions exist; L1, L2, … are the free ions including free metal ion, free ligands and other free ions besides H+ and OH-.
After substituting the concentration of each ion with the above expression, the variables can be greatly decreased when the thermodynamic model is established based on both mass balance and charge balance equations, which makes solving the nonlinear equations on a computer more convenient and easy. TANG et al defined the whole process as the exponential computation method. The exponential computation method is also used in this research.
2.3 Dissolving characteristic of Cu2(OH)2CO3
The equilibrium among the copper-containing species dissolved in the solution and the simple ions (Cu2+, NH3, OH-, H+, Cl-, CO32-) can be expressed as the following equation:
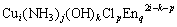 =
=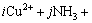
 i=1, 2; j=0, 1, 2, 3, 4, 5;
i=1, 2; j=0, 1, 2, 3, 4, 5;
k=0, 1, 2, 3, 4; p=0, 1; q=0, 1, 2, 3 (1)
 (2)
(2)
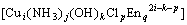 =
=
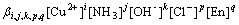 (3)
(3)
where [x] is the concentration of the species in the solution.
When the solid of Cu2(OH)2CO3 is in equilibrium with the solution, H2CO3 will be formed and will be in equilibrium with CO2 in the air:
CO2(g)+H2O=H2CO3 K=10-1.55
 (4)
(4)
The partial pressure of CO2 in the atmosphere is p(CO2)=1.01×102.5 MPa. The concentration of H2CO3 in solution is calculated to be 10-5.05 from Eq.(4). CO32- and HCO3- are also in equilibrium with H2CO3 and their concentrations are calculated to be [CO32-]=10-20.94[H+]-2 and [HCO3-]=10-11.38[H+]-1, respectively.
The dissolution equation of Cu2(OH)2CO3 can be written as
Cu2(OH)2CO3=2Cu2++2OH-+CO32- Ksp=10-33.78 (5)
[Cu2+]=10-33.78/2[OH]-1·[ CO32-]-0.5=
10-16.89×1014.18[H+]·[CO32-]-0.5 (6)
Substituting [CO32-]=10-20.94[H+]-2 into Eq.(6) yields
[Cu2+]=107.76[H+]2 (7)
Substituting Eq.(7) into Eq.(3) yields
[Cui(NH3)j(OH)kClpEnq2i-k-p]=
βi, j, k, p, q107.76i[H+]2i[NH3]j[OH-]k[Cl-]p[En]q=
exp(ln(βi, j, k, p, q107.76i)+jln[NH3]+(k-2i)ln10pH+
kln10pKw+pln[Cl-]+q[En])=
exp((ln(βi, j, k, p, q107.76i) +kln10pKw)+jln[NH3]+
(k-2i)ln10pH+pln[Cl-]+q[En])=
exp(A+Bln[NH3]+CpH+Dln[Cl-]+Eln[En])
where A=ln(βi, j, k, p, q107.76i)+kln10pKw; B=j; C=(k-2i)? ln10; D=p and E=q. Kw is the ion product of water.
The coefficients of A, B, C, D and E of each species are listed in Table 4.
Table 4 Coefficients of each species
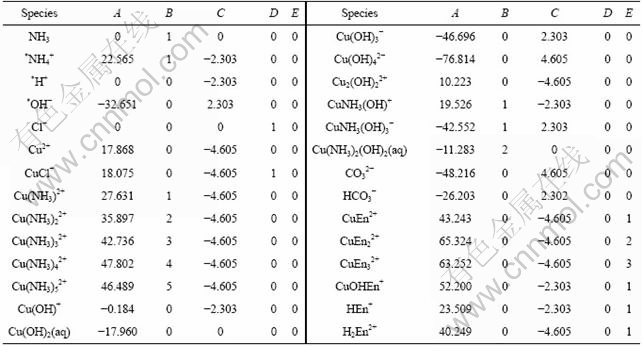
* [H+]=exp(-ln10pH); [NH4+]=109.8[NH3][H+]=exp(9.8ln10+ln[NH3]-ln10pH); [OH-]=10-14.18[H+]-1=exp(-14.18ln10+ln10pH)
The mass balance equations of copper, total ammonia, chloride and ethylenediamine can be expressed as

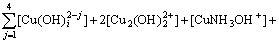
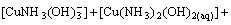
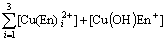 (8)
(8)

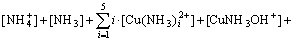
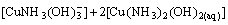 (9)
(9)
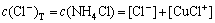 (10)
(10)
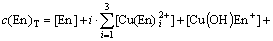
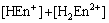 (11)
(11)
where c(Cu2+)T, c(NH3)T, c(Cl-)T and c(En)T are the total concentration of copper, ammonia, chloride and ethylenediamine in the solution, respectively. The total concentration of ammonia in the solution equals the concentration of ammonia c(NH3·H2O) plus ammonium chloride c(NH4Cl) added into the solution. And the total concentration of chloride equals the concentration of ammonium chloride.
The charge balance equation can be written as
∑m?[X]=0 (12)
where m and [X] mean the charge and the concentration of the ions in the solution, respectively.
After introducing the expression of [X]=exp(A+ Bln[NH3]+CpH+Dln[Cl-]+Eln[En]) into Eqs.(11)-(12) and giving the concentration of ammonia c(NH3·H2O), ammonium chloride c(NH4Cl) and ethylenediamine c(En)T as the operating conditions and varying from 0 to 5 mol/L, only five variables remain namely c(Cu2+)T, [NH3], pH, [Cl-] and [En]. The equation groups are solved with the soft ware of Matlab using the function of “flsove()”. The concentration of each species [X] is obtained from [X]=exp(A+Bln[NH3]+CpH+Dln[Cl-]+ E[En]).
3 Experimental
The verifying tests of solubility of each solid phase in the solution with different ammonia, ammonium chloride and ethylenediamine concentrations were carried out by adding 15 g pure Cu2(OH)2CO3 into 50 mL solution in bottles. The bottles were exposed to the atmosphere for many days to ensure CO2 saturation. All the bottles were placed on a constant-temperature shaking table and held at 298 K. The reagents used for preparing the solutions were all of analytical quality. The concentration of copper in the solution was analyzed by titration method and the solid undissolved in the solution was dried and weighed, and the phase composition was detected by X-ray diffraction.
4 Results and discussion
4.1 Thermodynamic characteristic of Cu2(OH)2CO3- NH3-NH4Cl-En-H2O system
The equation group of the thermodynamic model of Cu2(OH)2CO3-NH3-NH4Cl-En-H2O system was solved and the results of c(Cu2+)T, [NH3], [En], [Cl-], pH are shown in Fig.1. It can be seen that the total copper concentration dissolved in the solution increases with the increasing concentration of ethylenediamine. A low concentration of free ammonia, which is the guarantee to the decreasing evaporation rate of the ammonia to the air, can be kept when the concentration of ammonia added into solution is very low. However, a satisfactory solubility of Cu2(OH)2CO3 can also be attained by submitting ammonia with ethylenediamine.
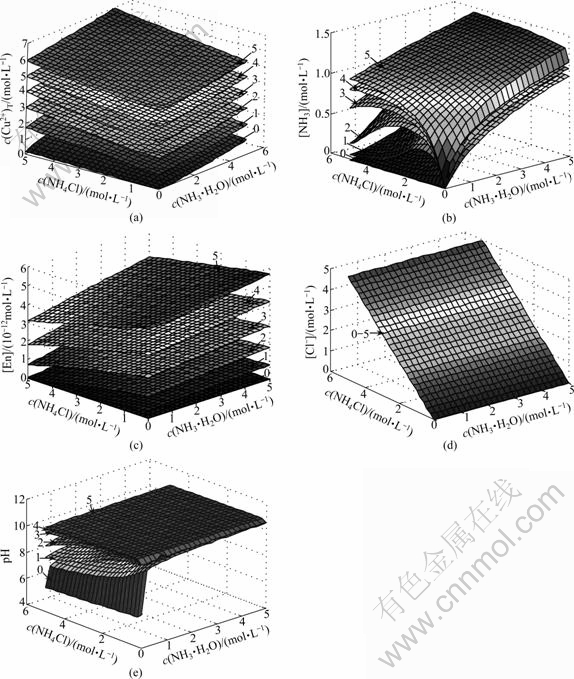
Fig.1 Equilibrium surface of concentration of copper, free ammonia, free En, free chloride and pH (The numbers signed in figures mean total concentration of ethylenediamine (mol/L)): (a) c(Cu2+)T; (b) [NH3]; (c) [En]; (d) [Cl-]; (e) pH
The solid of CuO, CuCO3, Cu3(OH)2(CO3)2 and Cu(OH)1.5Cl0.5 may be formed in the system of Cu2(OH)2CO3-NH3-NH4Cl-En-H2O. It is necessary to validate the possibility by comparing the concentration- product of each solid phase (Jsp) and the solubility- product constants(Ksp) of each solid phase.
The Jsp of CuO is calculated as
Jsp(CuO)=[Cu2+]?[OH]2 (13)
Introducing Eq.(7) into Eq.(13), there is
Jsp(CuO)=[Cu2+]?[OH]2=107.76[H+]2?[OH]2=
107.76?Kw2=10-20.6
The Jsp of CuO is smaller than its Ksp (Ksp of CuO is 10-19.51).
The Jsp of CuCO3 is calculated as
Jsp(CuCO3)=[Cu2+][CO32-]=
107.76[H+]2?10-20.94[H+]-2=10-13.18
It is apparent that Jsp of CuCO3 is smaller than its Ksp (Ksp of CuCO3 is 10-9.63).
The Jsp of Cu3(OH)2(CO3)2 is calculated as
Jsp(Cu3(OH)2(CO3)2)=[Cu2+]3[OH-]2[CO32-]2=
1023.28[H+]6[OH-]210-41.88[H+]-4=
10-18.6[H+]2[OH-]2=10-46.96
Jsp of Cu3(OH)2(CO3)2 is also smaller than its Ksp (Ksp of Cu3(OH)2(CO3)2 is 10-45.96).
From the above discussion, the Jsp of CuO, CuCO3 and Cu3(OH)2(CO3)2 are all smaller than their Ksp, which means that the formation of the solid of CuO, CuCO3 and Cu3(OH)2(CO3)2 is impossible in the system of Cu2(OH)2CO3-NH3-NH4Cl-En-H2O.
Another solid phase that may be formed is Cu(OH)1.5Cl0.5. Fig.2 shows the comparison between Jsp and Ksp of Cu(OH)1.5Cl0.5 in the system of Cu2(OH)2CO3- NH3-NH4Cl-En-H2O. It can be seen that, when the concentration of ethylenediamine is smaller than 2 mol/L, the concentration of ammonium chloride is relatively high and the concentration of ammonia is relatively low. The Jsp of Cu(OH)1.5Cl0.5 is larger than its Ksp, which means that in these areas Cu(OH)1.5Cl0.5 is formed. The stable areas of Cu(OH)1.5Cl0.5 and Cu2(OH)2CO3 are shown in Fig.3. The lines dividing these areas were fitted as Eqs.(14) and (15), respectively:
c(En)T=0 mol/L
c(NH4Cl)=1.707 06+0.991 73·c(NH3·H2O) mol/L
R2=0.997 66 (14)
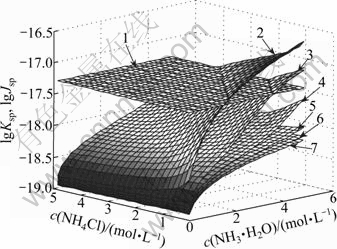
Fig.2 Comparison between lg Jsp and lg Ksp of Cu(OH)1.5Cl0.5: 1—lg Ksp; 2—lg Jsp(c(En)=0); 3—lg Jsp(c(En)=1 mol/L); 4— lg Jsp(c(En)=2 mol/L); 5—lg Jsp(c(En)=3 mol/L); 6— lg Jsp(c(En)=4 mol/L); 7—lg Jsp(c(En)=5 mol/L)
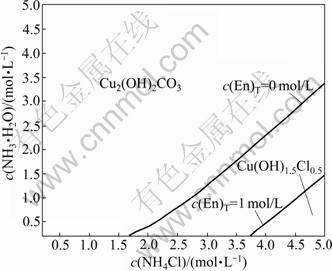
Fig.3 Stable area of Cu2(OH)2CO3 and Cu(OH)1.5Cl0.5
c(En)T=1 mol/L
c(NH4Cl)=3.512 17+1.006 49·c(NH3·H2O) mol/L
R2=0.999 57 (15)
4.2 Verifying tests
The X-ray diffraction patterns of the final solid, after being brought to equilibrium with solution of specific concentration of ammonia, ammonium chloride and ethylenediamine, are shown in Figs.4 and 5.
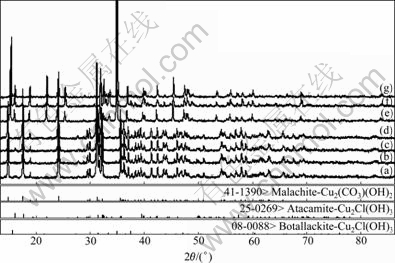
Fig.4 XRD patterns of final solid of different c(NH3·H2O) and c(NH4Cl) when c(En)T=0 mol/L: (a) Original Cu2(OH)2CO3; c(NH3·H2O) and c(NH4Cl) of (b)-(g) are 3, 2; 3, 4; 1, 2; 3, 5; 1, 3; 0, 5 mol/L, respectively
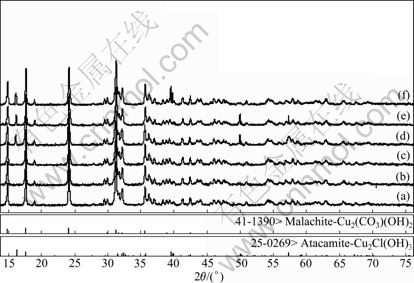
Fig.5 XRD patterns of final solid of different c(NH3·H2O) and c(NH4Cl) when c(En)T=1 mol/L: (a) Original Cu2(OH)2CO3; c(NH3·H2O) and c(NH4Cl) of (b)-(f) are 3, 2; 1, 1; 0.5, 4.5; 0, 5; 1, 5 mol/L, respectively
Figs.6-7 show the distributions of each tested final solid on the stable area images. And the final solid phase compositions are listed in Table 5. It is apparent that the experimental results are very coincident with the forecast by the thermodynamics model. A phenomenon must be especially explained. Using the f point in Fig.6 as an example, the final solid phase of this point is the mixture of Cu2(OH)2CO3 and Cu(OH)1.5Cl0.5 but not the pure Cu(OH)1.5Cl0.5 when the original c(NH3·H2O) and c(NH4Cl) are located at the Cu(OH)1.5Cl0.5 stable area. The reason is that the decreased concentration of ammonium chloride, which results from the decreased concentration of Cl- in the solution as Cu(OH)1.5Cl0.5 forms, leads to the movement of c(NH3·H2O) and c(NH4Cl) to the stable area of Cu2(OH)2CO3, and eventually ends the process of Cu2(OH)2CO3 transforming to Cu(OH)1.5Cl0.5 before Cu2(OH)2CO3 is vanished.
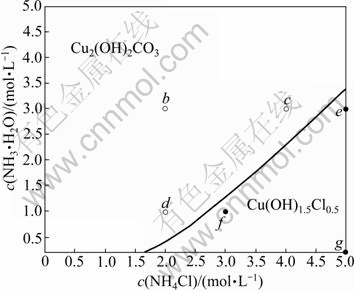
Fig.6 Distribution of point of tested final solid phase when c(En)T=0 mol/L
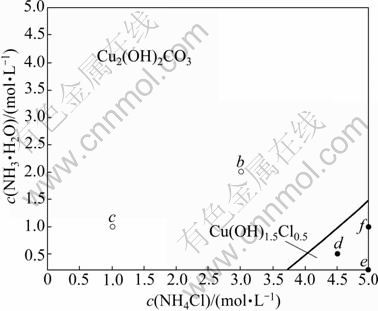
Fig.7 Distribution of point of tested final solid phase when c(En)T=1 mol/L
Table 5 Final solid phase composition of original solid phase of Cu2(OH)2CO3

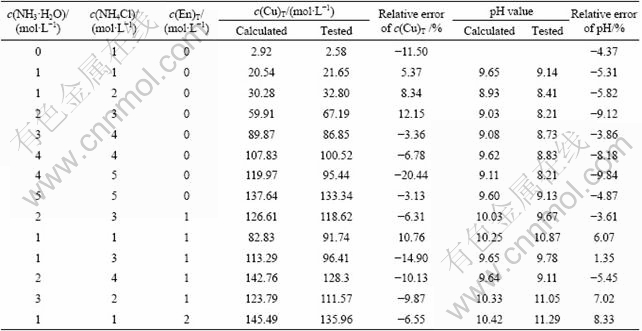
Both the calculated and experimental values of the concentration of copper dissolved in the solution and the pH of the solution under specific conditions when c(NH3·H2O), c(NH4Cl) and c(En)T are located at the stable area of the original solid are shown in Table 6. It is apparent that the thermodynamic model is correct and reliable because most of the relative errors of both copper concentration and pH value are less than 10%, which is satisfactory when the activity of the ions is approximated by their mole concentrations. Since the requirement of keeping the bottles open to the air to make sure that CO2 is saturated in the solution, the evaporation of ammonia also leads to high relative errors of copper concentration and pH value under some conditions.
Table 6 Results of verifying tests
The prediction of the concentration of copper when the final solid is a mixture is much more complex. It is not only a function of the concentration of ammonia and ammonium chloride but also related to the amount of the original solid. When different amounts of original solid are transformed to another solid, the consumption or contribution of Cl- is diverse.
5 Conclusions
A thermodynamic model describing the dissolution characteristics of Cu2(OH)2CO3 was established. Through the verifying tests, it is found that the thermodynamic model is correct and reliable. The model is helpful to the leaching process when choosing lixiviant with the appropriate concentration of ammonia, ammonium chloride and ethylenediamine. Furthermore, the stable area diagrams of each phase are also useful to the precipitation and the synthesizing of the copper salts.
References
[1] LIMPO J L, FIGUEIREDO J M, AMER S L. The CENIM-LNETI process: A new process for the hydrometallurgical treatment of complex sulphides in ammonium chloride solutions [J]. Hydrometallurgy, 1992, 28(2): 149-161.
[2] OLPER M. The EZINEX.RTM. process [C]// WARREN G W. EPD Congress. Warrendale, PA: The Minerals, Metals and Materials Society, 1994: 513-519.
[3] FANG J J, LI Y F, LU X L, ZHANG E B. Effects and industry application of ammonia leaching of low copper oxide ore under normal temperature and pressure [J]. Mining and Metallurgical Engineering, 2008, 28(3): 27-38. (in Chinese)
[4] WANG C Y. Exploration of rebellious low-grade copper oxide ore with high alkality gangues [J]. Mining and Metallurgy, 2001, 10(4): 49-52. (in Chinese)
[5] ZHANG Y Z, YANG X W. The solubilities of poorly soluble electrolytes in complex solutions [J]. Hydrometallurgy, 1998, 50(1): 103-110.
[6] YARTASI A, COPUR M. Dissolution kinetics of copper(II) oxide in ammonium chloride solutions [J]. Minerals Engineering, 1996, 9(6): 639-698.
[7] EKMEKYAPAR A, OYA R. Dissolution kinetics of an oxidized copper ore in ammonium chloride solution [J]. Chemical and Biochemical Engineering Quarterly, 2003, 17(4): 261-266.
[8] LI D L, WANG D Z, FINCH J A. Selectively leaching Cu(Ⅱ) and Ni(Ⅱ) from acid mine drainage sludge by using ethylenediamine-ammonium sulfate [J]. Transactions of Nonferrous Metals Society of China, 2002, 12(6): 1176-1179.
[9] RAMDANE S. A rigorous calculation method for determining potential-pH diagrams (Part I): Copper in aqueous solutions of various complexing agents [J]. Iran J Chem Chem Eng, 2005, 24(3): 29-39.
[10] SERDAR A, FIONA M D. Electrochemistry of copper in aqueous ethylenediamine solutions [J]. Journal of the Electrochemical Society, 2002, 149(7): B340-B347.
[11] TANG M T, ZHAO T C. A thermodynamic study of the basic and negative potential fields of the systems of Sb-S-H2O and Sb-Na-S-H2O [J]. Journal of Central-South Institute of Mining and Metallurgy, 1988, 19(1): 35-43. (in Chinese)
[12] YANG S H, TANG M T. Thermodynamics of Zn(Ⅱ)-NH3-NH4Cl- H2O system [J]. Transactions of Nonferrous Metals Society of China, 2000, 10(6): 830-833.
[13] WANG R X, TANG M T, YANG J G, YANG S H. Thermodynamics of Zn(Ⅱ) complex equilibrium in system of Zn(Ⅱ)-NH3-Cl-- CO32--H2O [J]. The Chinese Journal of Nonferrous Metals, 2008, 18(s1): 192-198. (in Chinese)
[14] ROBERT M S, ARTHUR E M. Critical stability constants: Inorganic complexes [M]. Vol.4. New York and London: Plenum Press, 1976.
[15] SILLEN L G, MARTELL A E. Stability constants of metal-ion complexes [M]. Special Publications N17 and 25. London: Chemical Society, 1964.
Foundation item: Project(2007CB613604) supported by the National Basic Research Program of China; Project(50674104) supported by the National Natural Science Foundation of China
Corresponding author: LIU Wei; Tel/Fax: +86-731-88830470; E-mail: ase.6520@163.com
DOI: 10.1016/S1003-6326(09)60143-6
(Edited by YUAN Sai-qian)