J. Cent. South Univ. Technol. (2008) 15(s1): 029-032

DOI: 10.1007/s11771-008-308-0

Vibrational shear flow of anisotropic viscoelastic fluid with small amplitudes

HAN Shi-fang(韩式方)

(Chengdu Institute of Computer Application, Chinese Academy of Sciences, Chengdu 610041, China)

Abstract: Using the constitutive equation of co-rotational derivative type for anisotropic viscoelastic fluid-liquid crystalline (LC), polymer liquids was developed. Two relaxation times are introduced in the equation: λ_n represents relaxation of the normal-symmetric stress components; λ_s represents relaxation of the shear-unsymmetric stress components. A vibrational rotating flow in gap between cylinders with small amplitudes is studied for the anisotropic viscoelastic fluid-liquid crystalline polymer. The time-dependent constitutive equation are linearized with respect to parameter of small amplitude. For the normal-symmetric part of stress tensor analytical expression of the shear stress is obtained by the constitutive equation. The complex viscosity, complex shear modulus, dynamic and imaginary viscosities, storage modulus and loss modulus are obtained for the normal-symmetric stress case which are defined by the common shear rate. For the shear-unsymmetric stress part, two shear stresses are obtained thus two complex viscosities and two complex shear modulus (i.e. first and second one) are given by the constitutive equation which are defined by rotating shear rate introduced by author. The dynamic and imaginary viscosities, storage modulus and loss modulus are given for each complex viscosities and complex shear modulus. Using the constituive equation the rotating flow with small amplitudes in gap between two coaxial cylinders is studied.

Key words: un-symmetric constitutive equation; anisotropic viscoelastic fluid; liquid crystalline polymer; vibrational shear flow with small amplitudes

1 Introduction

It is important to study the unsteady vibrational rotating flow with small amplitudes^[1-2], as the time-dependent experiments of the LC polymer are considered a best way to obtain knowledge of elasticity of the materials, i.e. dynamic viscoelasticity. In the present paper on the basis of the constitutive equation of co-rotational type^[3-4], the vibrational rotating flow in gap between cylinders with small amplitudes is investigated for the anisotropic viscoelastic fluid-liquid crystalline polymer. The complex viscosity, complex shear modulus, dynamic and imaginary viscosities, storage modulus and loss modulus are obtained for both normal-symmetric stress and shear-unsymmetric stress cases.

2 Un-symmetric constitutive equation

Time-dependent rotating flow of anisotropic fluid in tube or in gap between coaxial cylinders is studied. The cylindrical coordinate system (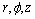) is used. The velocity field is assumed to be of A concept of anisotropic viscoelastic simple fluid is

                         (1)

introduced by HAN^[3-4] according to which instead of velocity gradient tensor D in the classic theory, the stress tensor is described by first Rivlin-Ericksen tensor A and spin tensor W measured with respect to co-rotational coordinate system. Using the principle and extending the general principle in constructing constitutive equation by Truesdell and constitutive equation of co-rotational Oldroyd fluid B, a general theory of the constitutive equation of the fluid is developed. The un-symmrtry of the stress tensor is defined by the un-symmrtry of the shear stress components. The stress tensor is split into symmetric and un-symmertric parts

                                (2)

For the fluid the constitutive equation is:

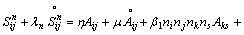
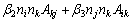                        (3)

where  n is symmetric stress components and s is un-ssymmetric components; Two relaxation times λ_n and λ_s are introduced, λ_n is the relaxation of normal-symmetric stress components; λ_s is the relaxation of shear- unsymmetric stress components; “o” is co-rotational time derivative.

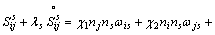
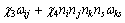                        (4)

where

.

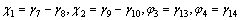3 Vibrational shear flow with small amplitudes

The vibrational rotating flow of anisotropic fluid in gap between cylinders with small amplitudes is studied. The velocity field of the flow is assumed to be of

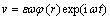,                  (5)

For the vibrational rotating flow, two shear rates are introduced, the general shear rate  and rotation shear rate, which are of magnitudes .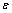

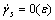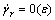,                          (6)

With help of the magnitude analysis linearization, the ordinary differential equation is completed which was derived from the normal-symmetric part of the constitutive equation. The following linear ordinary differential equation is obtained as follows:

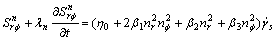  (7)

Solving Eqn.(7) the stress component 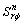 is obtained. For the normal-symmetric stress the complex viscosity is then given as

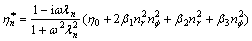      (8)

Splitting real and imaginary part in Eqn.(8), according to the definition 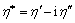, for the normal-symmetric stress the analytical expressions of dynamic and imaginary viscosities are given by

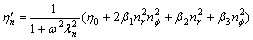     (9)

    (10)

According to the definition of complex shear modulus and complex viscosity (Eqn.(8)) for the normal- symmetric stress the complex shear modulus is derived as

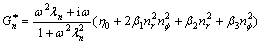   (11)

Splitting real and imaginary part in Eqn.(11) for the normal-symmetric stress storage modulus and loss modulus are obtained as follows:

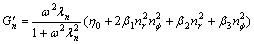    (12)

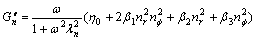    (13)

Similarly, using the magnitude analysis linearization, the ordinary differential equation is completed which was derived from the shear—unsymmetric part of the constitutive equation. The following linear ordinary differential equations are obtained as follows:

                 (14)

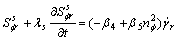                (15)

Solving Eqns.(14)-(15) the stress components are obtained for the shear—unsymmetric stresses:

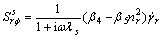，                 (16)

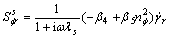                 (17)

Introducing two complex shear viscosities

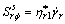,                      (18)

where 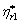  and 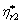 are two complex shear viscosities for the the shear—unsymmetric stresses called by first and second un-symmetric complex viscosity. A new shear rate, , is introduced by author, called by rotation shear rate. In the general theory of non-Newtonian fluid mechanics, only one shear rate 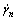 was introduced. In the present investigation, three shear rates are introduced. One is for normal-symmetric stress, another two for shear—unsymmetric stresses. Two rotation complex viscosities are derived, the first and second complex shear viscosities are obtained by Eqns.(16)-(18).

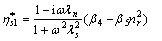                  (19)

                  (20)

Splitting real and imaginary part in Eqn.(19), according to the definition 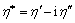, for the first complex shear viscosity and shear—unsymmetric stress part, the analytical expressions of dynamic and imaginary viscosities are given by

                  (21)

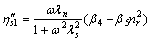                  (22)

Splitting real and imaginary part in Eqn.(20), according to the definition 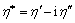, for the first complex shear viscosity and shear—unsymmetric stress part the analytical expressions of dynamic and imaginary viscosities are given by

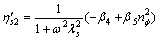                  (23)

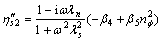                  (24)

According to the definition of complex shear modulus and the complex viscosity Eqns.(19)-(20), for the shear—unsymmetric stress part, the analytical expressions of first and second complex modulus are derived as follows:

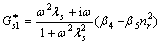                  (25)

                (26)

Splitting real and imaginary part in Eqn.(25), for the shear un-symmetric stress part, the storage modulus and loss modulus are obtained for the first complex modulus as follows:

                    (27)

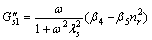                   (28)

Splitting real and imaginary part in Eqn.(26), for the shear—unsymmetric stress part, the storage modulus and loss modulus are obtained for the second complex modulus as follows:

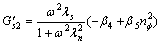                  (29)

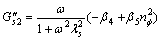                  (30)

4 Results and conclusions

On the basis of the constitutive equation of co-rotational derivative type for anisotropic viscoelastic fluid－LC polymer liquids developed by HAN, using physic-rheological analysis of the fluid a vibrational rotating flow in gap between cylinders with small amplitudes is studied for the anisotropic viscoelastic fluid-liquid crystalline polymer. In the equation two relaxation times are introduced: λ_n represents relaxation of the normal-symmetric stress components; λ_s represents relaxation of the shear—unsymmetric stress components. The computational manipulation is used to get the analytical expressions.

For the shear—unsymmetric stress part the first and second complex shear viscosities are derived by the first and second un-symmetric shear stress components. Because of non-symmetry of the stress tensor three complex shear modulus are introduced: 1) the complex viscosity  with action of normal-symmetric stress; 2) the complex viscosities 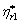 and 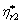 with action of shear un-symmetric stresses. For anisotropic fluid stress components should be of sum of normal-symmetric stress and shear un-symmetric stress components.

Fig.1 shows the storage modulus 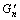(a) and loss modulus 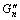(b) vs oscillation amplitude ω with action of normal-symmetric stress (with variation of the director angle, η₀=5.0, λ_n=0.5, β₁=1.50, β₂=1.0, β₃=2.0). It can be seen from Fig.1, that the curve of the storage modulus 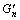and loss modulus  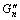vs oscillation amplitude ω oscillate with the director angle. Fig.2 and Fig.3 show the storage modulus and loss modulus vs oscillation amplitude ω with action of shear un-symmetric stress derived from the first and second rotation complex viscosities(with variation of director angle, λ_s=0.50, β₄= 1.50, β₅=1.0). It can be seen from Fig.1 to Fig.3 that the

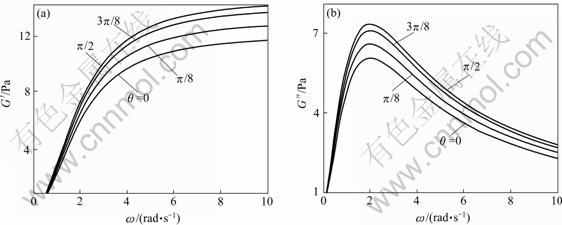
Fig.1 Storage modulus 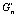(a) and loss modulus 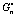(b) vs oscillation amplitude with action of normal-symmetric stress

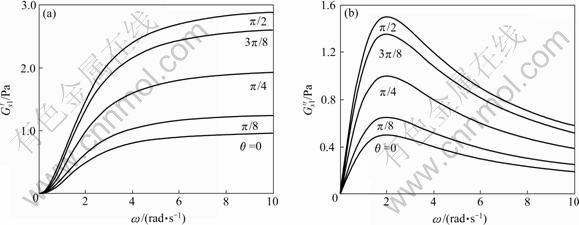
Fig.2 Storage modulus 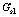 and loss modulus  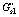vs oscillation amplitude obtained by first rotational complex viscosity

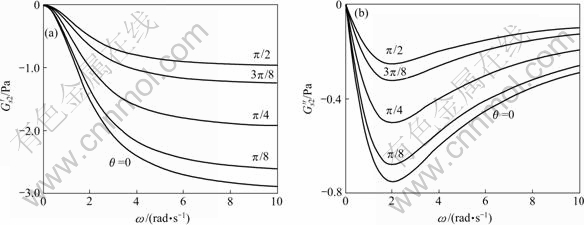
Fig.3 Storage modulus and loss modulus  vs oscillation amplitude obtained by second rotational complex viscosity

director tumbling may change magnitudes of the storage modulus and loss modulus, but do not change the general tendency of the curves^[5]. The present new theoretical results and conclusions, such as non-symmetric stress components and 3 complex viscosities and modulus, are in agreement with non- symmetric viscoelasticity derived by VOLKOV and KULICHIKHIN^[6-7]. Computational manipulation was used in Ref.[8].

References

[1] CHEN Meng-fang. Non-newtonian fluid mechanics[M]. Beijing: Science Press, 1987. (in Chinese)

[2] JIANG Ti-qian. Chemical engineering rheology[M]. Shanghai: East China University of Science and Technology Press, 2004. (in Chinese)

[3] HAN Shi-fang. Continuum mechanics of anisotropic non-Newtonian fluids—Rheology of liquid crystalline polymer[M]. Beijing: Science Press, 2008.

[4] HAN Shi-fang. An unsymmetric constitutive equation for anisotropic viscoelastic fluid[J]. Acta Mechanica Sinica, 2007, 23(2): 149-158.

[5] LARSON R G. Arrested tumbling in shearing flows of liquid crystal polymers[J]. Macromolecules, 1990, 23: 3983-3992.

[6] VOLKOV V S, KULICHIKHIN V G. Non-symmetric viscoelasticity of anisotropic polymer liquids[J]. J Rheol, 2000, 39(3): 360-370.

[7] VOLKOV V S, KULICHIKHIN V G. Anisitropic viscoelasticity of liquid crystaline polymers[J]. J Rheol, 1990, 34(3): 281-293.

[8] ROESNER KG. The impact of computer algebra on fluid dynamics[C]// Proc 2nd European Fluid Mechanics Conference. Warsaw: General Review Lecture, 1994.

(Edited by CHEN Ai-hua)

Foundation item: Project(10772177) supported by the National Natural Science Foundation of China

Received date: 2008-06-25; Accepted date: 2008-08-05

Corresponding author: HAN Shi-fang, Professor; Tel: +86-28-66142335; E-mail: sfh5578@sina.com