J. Cent. South Univ. Technol. (2008) 15(s1): 093-097
DOI: 10.1007/s11771-008-322-2
Rheological properties of salt-tolerant HPAM solutions with ultrahigh molecular weight
ZHANG Min-ge(张敏革)1, ZHANG Lü-hong(张吕鸿)1, JIANG Bin(姜 斌)1, 2, LI Xin-gang(李鑫钢)1, 2
(1. School of Chemical Engineering and Technology, Tianjin University, Tianjin 300072, China;
2. National Engineering Research Centre for Distillation Technology, Tianjin 300072, China)
Abstract: The rheological properties of salt-tolerant partially hydrolyzed polyacrylamide (HPAM)solutions with molecular of 2.5×107 g/mol at different concentrations were measured in steady-state shear flow mode by Haake Rheostress 150 rheometer. Three constitutive equations (Oldroyd four constant model, Guesekus model and FENE-P model) were used for describing the apparent viscosity and first normal stress difference. The apparent viscosity of salt-tolerant HPAM solutions appears a first Newtonian zone when the shear rate is approximately lower than 0.2 s-1. At high shear rate, the HPAM solutions show shear-thinning and elasticity. The results show that the FENE-P model has the best agreement between theoretical and experimental data within the available shear rate range. The material parameters are useful for numerical analysis of polymer solution flow fields.
Key words: salt-tolerant partially hydrolyzed polyacrylamide; steady-state flow; shear thinning; FENE-P model
1 Introduction
At present, polymer flooding is one of the most effective technologies to enhance the crude oil recovery (EOR) and develops rapidly. Salt-tolerant partially hydrolyzed polyacrylamide (HPAM) with ultrahigh molecular weight, which has good viscosifying properties and well-known physicochemical characteristics, has been widely used in EOR as agent in China. ZHANG et al[1] researched the rheological behavior of HPAM solutions with ultra molecular and found that, polymer solutions had properties of shear thinning and elasticity in steady shear flow. Till now, the power law model, developed by OSTWALD and DEWAELE, was the most commonly used model to describe the properties of polyacrylamide solutions[2]. However, this model can only reflect the viscosity of the polymer solution but can not describe the elasticity.
In this study, a proper constitutive equation was selected and their material parameters for describing the viscoelasticity of solt-tolerant HPAM solutions with unltrahigh molecular weight were determined based on the rheological experiments. The constitutive equation will be used to simulate the flow process of polymer solution in an equipment unit of the polymer flooding technologies. Rheological constitutive equations relate to strain, strain rate and strain history in flow material, except for generalized Newtonian fluids and Hooke solids. Rheological constitutive equations are almost nonlinear and complex. We must take into account a number of constraints and compromise between the agreement with rheometrical data as well as the simplicity of the model together with its associated computational cost[3]. So in this paper the steady shear viscosity and the first normal stress difference N1 were considered. The steady rheological properties of salt-tolerant partially hydrolyzed polyacrylamide solution with molecular weight of 2.5×107 at concentration of 3 000 mg/L to 7 000 mg/L were measured. Three constitutive equations(Oldroyd four constant model, Guesekus model and FENE-P model) were applied to fit the experimental data, proper constitutive equation was chosen and decided based on its coincide degree with the experimental data.
2 Materials and rheological measurements
The average molecular weight of salt-tolerant HPAM solution was 2.5×107, the degree of hydrolysis was 25%-30%, and the solid content was 90%. The solutions were prepared by adding a known amount of polymer powder to 300 mL distilled water at room temperature (about 13 ℃). The solution concentrations were 3 000, 5 000, 6 000 and 7 000 mg/L, respectively, which were measured on a cone and plate system with the diameter of 17.5 mm and a cone angle of 1?. The first normal stress difference was carried out on a cone and
plate system with the diameter of 10 mm and a cone angle of 1?. The gap between cone and plate of the two systems was 0.052 mm. According to the cone angle, the shear rate  , apparent viscosity ηa and first normal stress difference N1 is calculated by:
, apparent viscosity ηa and first normal stress difference N1 is calculated by:
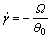 (1)
(1)
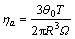 (2)
(2)
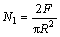 (3)
(3)
where Ω is the angular velocity, rad/s; θ0 is the angle between flat plate and cone surface, rad; T is torque, N?s; R is the diameter of the cone, m; and F is the normal force, N.
3 Constitutive equations
It was found that the viscosity of salt-tolerant HPAM solution with ultra molecular weight decreased with the increase of shear rate, and the first normal stress difference N1 increased significantly when the shear rare increased, which were similar to the properties of most of the polymer solutions[1]. So, in this paper, our examinations focused on the constitutive equations, which describe the shear-thinning properties as well as elasticity.
3.1 Oldroyd four constant model
The Oldroyd-B model is a type of differential constitutive equations. It is a simple linear viscoelastic model for dilute polymer solutions based on the assumption that polymers can be modeled as Hookean springs[4], and consequently it allows for infinite extension of polymer molecules. The Oldroyd-B model is failed to predict shear-thinning rheological properties. However, when the model is extended to multi- parameters model, such as the Oldroyd four constant model, it does well in predicting steady-state shear viscosity, first and second normal stress difference which explains the fact that the Oldroyd four constant model is widespread used in simulation[5-6]. The Oldroyd four constant model is given below:
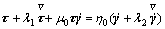 (4)
(4)
where τ is the extra stress tensor; λ1 is the relaxation time of the fluid, s; λ2 is the retardation time, s; η0 is the zero viscosity, Pa?s; and  is the shear rate.
is the shear rate.
The substitution of the simple steady-shear velocity field is
vx= y, vy=vz=0 (5)
y, vy=vz=0 (5)
Eqn.(4) gives for the shear viscosity:
 (6)
(6)
And the first normal stress difference is given as follows:
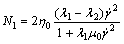 (7)
(7)
3.2 Giesekus model
The Giesekus model is one of the simplest differential constitutive equations that qualitatively describe the rheological behavior of polymer solution[7]. NAKAMURA et al[8] found that the Giesekus model could quantitatively agree with the experimental data for 0.2% aqueous solution of Polyacrylamide(PAA) and for 1.0% aqueous solution of Carboxymethyl cellulose (CMC). The Giesekus model is:
 (8)
(8)
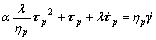 (9)
(9)
Here τp denotes the polymer part of the stress tensor, while τs is the Newtonian contribution from the solvent with viscosity ηs, λ is a relaxation time and ηp is viscoelastic contribution of viscosity, α is the mobility, which is a measurement of the importance of anisotropic hydrodynamic drag on the macromolecules.
The substitution of the simple steady-shear velocity field in Giesekus model gives for the shear viscosity as follows:
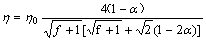 (10)
(10)
And the first normal stress difference is:
 (11)
(11)
where
 (12)
(12)
3.3 FENE-P model
The FENE-P model provides an improvement of the simple linear model, because it is able to reproduce some features of polymer solutions like the shear-thinning. Moreover, in numerical simulations, a finite molecular extensibility reduces the onset of numerical instabilities associated with strong gradients of the conformation tensor field. For these reasons, FENE-P model is usually adopted in numerical simulations of viscoelastic flows[9-11]. A kinetic theory expression for the extra-stress tensor is given by the sum of the two parts:
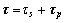 (13)
(13)
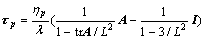 (14)
(14)
where L2 represents the extensibility of the dumbbells, A is a nondimensional configuration tensor, the governing equation for tensor A is as follows:
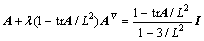 (15)
(15)
the substitution of the simple shear velocity field in the FENE-P model gives the shear viscosity as follows:
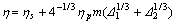 (16)
(16)
where
 (17)
(17)
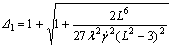 (18)
(18)
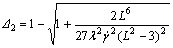 (19)
(19)
and the first normal stress difference is:
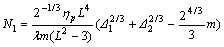 (20)
(20)
4 Results and discussions
4.1 Rheological properties of HPAM solution at steady-shear flow
The plot of apparent viscosity versus shear rate at the range of 0.01-1 000 s-1 is shown in Fig.1. It can be

Fig.1 Relationship between apparent viscosity and shear rate of salt tolerant HPAM solution
seen that, at low shear rates (approximately lower than 0.2 s-1), the apparent viscosity ηa exhibits a Newtonian plateau as ηa has a little change when the shear rate is increased. At this time, the apparent viscosity in the Newtonian plateau at the HPAM concentrations of 3 000, 5 000, 6 000 and 7 000 mg/L are 21.5, 55.0, 64.0 and 75.0 Pa?s respectively. At higher shear rate, the apparent viscosity decrease significantly and monotonically, which shows a shear-thinning behavior. In addition, the apparent viscosity increases with the increase of the concentration of the HPAM solution. Fig.2 shows the first normal stress difference N1 as a function of shear rate over the range of 100-1 000 s-1. It is found that, the first normal stress difference increases with increase of the shear rate and HPAM solution concentrations, which indicates that the elasticity of the solution is enhanced as the shear rate or HPAM solution concentration increases.
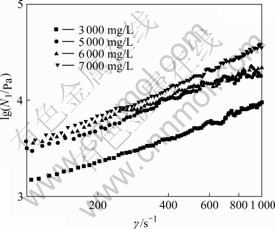
Fig.2 Relationship between first normal stress difference and shear rate of salt-tolerant HPAM solutions
4.2 Selection of constitutive equations and their material parameters
The material parameters for the three constitutive equations are determined by least square method. Fig.3 show the comparison of theoretical apparent viscosity for the three models with experimental data. It can be seen that, the predictions of the three constitutive equations are able to fit the experimental data at high shear rate. All of the three constitutive equations show the first Newtonian zone at lower shear rate. However, only the predicted value of FENE-P model is close to the experiment data. Fig.4 shows the comparison of theoretical data with experimental results in first normal stress difference for the three constitutive equations. It is found that, compared with the Oldroyd four constant model and Giesekus model, the FENE-P model still has the best agreement with the experimental data. Figs.5 and
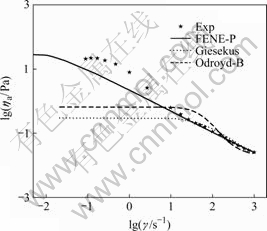
Fig.3 Comparison of theoretical apparent viscosity of different models with experimental data at 15 ℃
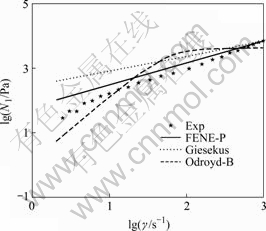
Fig.4 Comparison of theoretical first normal stress difference of different models with experimental data at 15 ℃
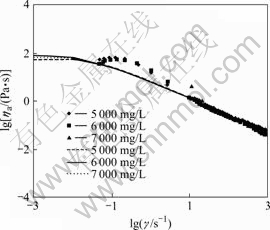
Fig.5 Apparent viscosity: experimental(scattered points) and theoretical data for FENE-P model
6 show the comparison of FENE-P model predictions

Fig.6 First normal stress difference: experimental (scattered points) and theoretical data for FENE-P model
and the experiment data (apparent viscosity and first normal stress difference) at the HPAM concentration of 5 000 mg/L, 6 000 mg/L and 7 000 mg/L, which indicates that the FENE-P model can describe the rheological properties of HPAM solution over the investigated concentration range in this study.
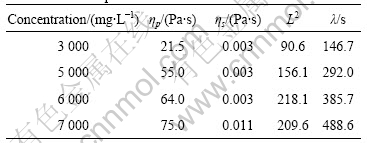
Table 1 shows the material parameters of the FENE-P model at various HPAM solution concentration investigated in this study. It can be seen that, ηs is small, which is almost irrelevant to concentration of HPAM solutions. However, ηp, L2 and λ are concentration dependent obviously and increase significantly with the increase of concentration of HPAM solutions, which reflects that the higher the concentration is, the larger the viscoelasticity of the HPAM solution will be.
The proper constitutive equation FENE-P model and its material parameters are important for dynamic prediction of numerical simulations in polymer flooding Technology, as well as in the design of polymer flooding projects.
Table 1 Material parameters of FENE-P model
5 Conclusions
1) The rheological properties of salt-tolerant HPAM solution with super high molecular weight are conducted at steady-state shear mode. The apparent viscosity of salt-tolerant HPAM solutions shows the first Newtonian zone when the shear rate is approximately lower than 0.2 s-1 as ηa is almost independent of the shear rate. At higher shear rate, the HPAM solution investigated in this paper shows shear-thinning behavior and elasticity. Over the range of shear rate of available experimental data, the apparent viscosity and first normal stress difference increase with the increase of concentration of the HPAM solutions.
2) Compared with the Oldroyd four constant model and Giesekus model, the FENE-P model provides the best agreement between experimental and theoretical data for steady-state flow at the concentration range of 3 000 mg/L to 7 000 mg/L. The material parameters ηv in FENE-P model is small, which is almost irrelevant to concentration of HPAM solutions. And the material parameters ηv, L2 and λ increase significantly with the increase of the concentration of HPAM solutions.
3) The selected constitutive equation and its material parameters are important for numerical analysis of polymer solution flow fields.
References
[1] ZHANG Lu-hong, ZHANG Dan, JIANG Bin. The rheological behavior of salt tolerant polyacrylamide solutions [J]. Chem Eng Technol, 2006, 29(3): 395-400.
[2] ILIUTA I, LARACHI F. Hydrodynamics of power-law fluids in trickle-flow reactors: Mechanistic model, experimental verification and simulations [J]. Chem Eng Sci, 2002, 57(11): 1931-1942.
[3] PURNODE B, CROCHET M J. Polymer solution characterization with the FENE-P model [J]. J Non-Netonian Fluid Mech, 1998, 77(1/2): 1-20.
[4] WEI Jin-jia, YAO Zhi-qiang. Rheological characteristics of drag-reducing surfactant solution [J]. Journal of Chemical Industry and Engineering (China), 2007, 58(2): 335-340. (in Chinease)
[5] YE Zhou-yuan, HONG Liang, LIU Xi-ling, YIN Tu-bing. Constitutive model of rock based on microstructures simulation [J]. J Cent South Univ Technol, 2008, 15(2): 230-236.
[6] BARIS S. Steady flow of an Oldroyd 4-constant fluid in a corner region formed by two planes [J]. Turk J Engin Environ Sci, 2001, 25(6): 587-594.
[7] YOO J Y, CHOI H Ch. On the steady simple shear flows of the one-mode Giesekus fluid [J]. Rheol Acta, 1989, 28(1): 13-24.
[8] NAKAMURA K, MORI N, YAMAMOTO T. Examination of constitutive equations for polymer solutions [J]. J Text Mach Soc Japan, 1992, 38(2): 31-38.
[9] PURNODE B, CROCHET M J. Flows of polymer solutions through contractions Part I: Flows of polyacrylamide solutions through planar contractions [J]. J Non-Newtonian Fluid Mech, 1996, 65(2/3): 269-289.
[10] CHENG Y, MUNEKATA M, MATSUZAKI K, OHBA H. Numerical analysis of viscoelastic flow based on FENE-P model using high-order accuracy finite difference method [J]. Technical Reports of the Kumamoto University, 1999, 48(2): 381-393.
[11] IU A W, BORNSIDE D E, ARMSTRONG R C, BROWN R A. Viscoelastic flow of polymer solutions around a periodic, linear array of cylinders: comparisions of predictions for microstructure and flow fields [J]. J Non-Newtonian Fluid Mech, 1998, 77(3): 153-190.
(Edited by ZHAO Jun)
Foundation item: Project(07JCZDJC02600) supported by the Natural Science Foundation of Tianjin, China
Received date: 2008-06-25; Accepted date: 2008-08-05
Corresponding author: ZHANG Lü-hong, PhD; Tel: +86-22-27400199; E-mail: zhanglvh@tju.edu.cn