自适应遗传算法优化模糊变权重的复杂系统时间序列组合预测方法
李冠南1, 2,单汨源1
(1. 湖南大学 工商管理学院,湖南 长沙,410082;
2. 长沙市公安局 科技处,湖南 长沙,410005)
摘要:针对复杂系统时间序列预测精度不高问题,将复杂系统时间序列组合预测模型的权系数视为模糊数,以模糊区间的大小作为模糊变权重复杂系统时间序列组合预测模型目标函数,利用自适应遗传算法优化复杂系统时间序列组合预测模型目标函数的权重系数,建立基于遗传算法优化模糊变权重的复杂系统时间序列组合预测方法。仿真结果表明:此模糊自适应变权重非线性组合预测模型的精度较高,并且平均误差和预测平方根误差均较小;所提出的基于遗传算法优化模糊变权重组合预测模型的最大相对误差为2.89%,小于各预测模型中最小的最大相对误差3.24%,且平均误差和平方根误差均较小。
关键词:复杂系统;预测模型;组合预测;模糊变权重
中图分类号:O211.67;TM715 文献标志码:A 文章编号:1672-7207(2013)11-4542-06
Combined forecasting model on time series of complex systems based on fuzzy variable weight optimized by adaptive genetic algorithm
LI Guannan1, 2, SHAN Miyuan1
(1. School of Business Administration, Hunan University, Changsha 410082, China;
2. Department of Science and Technology of Changsha Municipal Public Security Bureau, Changsha 410005, China)
Abstract: As for the low forecasting precision problem about time series in complex system, a time series combined forecasting model of complex systems was established based on the method of fuzzy variable weight optimized by adaptive genetic algorithm, meanwhile the model was handled by using of some measurements such as combined forecasting model of weight being regarded as fuzzy numbers, objective function of combined forecasting model on time series of complex systems due to fuzzy variable weight based on the fuzzy interval size and the weight of the combined forecasting model optimized by adaptive genetic algorithm. The simulation results show that the precision of nonlinear combined forecasting model is higher than that of every single combined forecasting model. The most relative error value of the combined forecasting model is 2.89%, which is less than the least value 3.24% of the most relative error of the single forecasting model, and the mean error and square root error of the combined forecasting model is less.
Key words: complex systems; forecasting model; combination forecasting; fuzzy variable weight
复杂系统往往存在内部结构复杂、多因素耦合影响和评价指标较多等问题[1-3],若采用单个时间序列预测模型或部分因素和指标对复杂系统的输入、输出进行预测,则存在仅能体现所研究复杂系统的局部,而不能体现复杂系统信息源的广泛性且对模型参数设定形式敏感等缺点。相反,若采用多个不同的时间序列预测模型的有效组合,则可充分利用各种信息,达到有效提高复杂系统预测精度与模拟评价效果的目的[4-6]。Bates等[7]提出的组合预测方法为有效地提高复杂系统时间序列预测精度提供了新思路,受到国内外预测工作者的重视。目前,国内外学者提出的各种不同组合预测方法一般可分为线性组合预测和非线性组合预测两大类。由于线性组合预测比较简单,故研究成果最多,也最为人们所常用。但对于非线性时间序列组合预测而言,作为只是不同预测方法之间预测值的一种凸组合的线性组合预测方法往往存在预测结果“时好时坏”的局限性,为此,李学全等[8]提出了一些非线性组合预测方法,并认为在某种测度下不同预测方法的非线性组合函数的度量要比单个预测函数的度量优越。鄂加强等[9]引入了各预测方法的预测相对误差、预测对象的变化趋势、灰色基本权重和自适应调节系数等概念,建立了模糊自适应变权重非线性组合预测模型,但其权重系数尚有待于进一步优化。在实际应用中,如何构造出有效的非线性组合函数和求出各种预测方法的权系数十分困难[10-12]。近年来,模糊系统理论在非线性系统控制、预测、辨识等方面的研究表明[13],模糊模型作为一种结构型数字估计器本质上是一种非线性模型,同时具有极强的泛化能力和适应能力,可为模糊理论与复杂系统时间序列组合预测有效融合提供很好的新思路。为此,本文作者将模糊变权重应用于复杂系统时间序列组合预测中,将复杂系统时间序列组合预测各模型的权重系数视为模糊数,利用遗传算法来优化复杂系统时间序列组合预测模型的权系数。
1 基于遗传算法优化模糊变权重的复杂系统时间序列组合预测模型
1.1 模糊变权重的复杂系统时间序列组合预测模型的建立
记yij(i=1, 2, …, K; j=1, 2, …, n)表示第i种复杂系统时间序列预测方法在j时刻的预测值,则K种复杂系统时间序列预测方法的组合预测值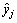 为
为
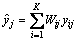 ;j=1, 2, …, n (1)
;j=1, 2, …, n (1)
式中:Wij为第i种预测方法的权系数,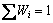 。将Wij看作一个三角模糊数[8],其隶属函数为
。将Wij看作一个三角模糊数[8],其隶属函数为
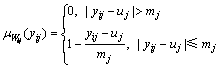 (2)
(2)
式中:uj为第i种复杂系统时间序列预测方法在j时刻的预测值的均值;mj为模糊子集的边界,用于确定权系数的隶属度必要条件,可以根据实际应用情况进行自适应调整,一般取mj=ε·σj;ε为调节系数,0<ε<3;σj为i种复杂系统时间序列预测方法在j时刻的预测值的方差,
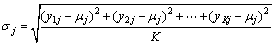 (3)
(3)
由模糊集理论可知,预测值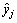 也是1个模糊数,且其隶属函数为
也是1个模糊数,且其隶属函数为
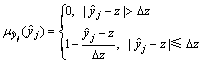 (4)
(4)
式中:z=∑uiyij,为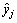 的中心参数;Δz=∑ε·σjyij,为
的中心参数;Δz=∑ε·σjyij,为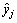 的幅度。
的幅度。
1.2 模糊变权重的复杂系统时间序列组合预测模型权重参数的确定
为使建立的模糊变权重的复杂系统时间序列组合预测模型的精度更高,须使其模糊区间达到最小,即模糊变权重的复杂系统时间序列组合预测模型的目标函数为
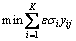 (5)
(5)
因为yij≈yj,ε·σj≥0,故模糊变权重的复杂系统时间序列组合预测模型的目标函数可近似等价为
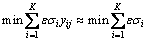 (6)
(6)
从式(6)可见:各模糊数Wij的模糊区间的大小是影响复杂系统时间序列预测精度的关键,εσj越小,则复杂系统时间序列预测精度越高。
在某一确定的水平值λj(0≤λj≤1)下,希望模糊变权重的复杂系统时间序列组合预测值的隶属函数值满足:
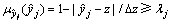 (7)
(7)
则j时刻的复杂系统时间序列组合预测值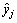 的变化区间为[z-(1-λj)Δz, z+(1-λj)Δz]。
的变化区间为[z-(1-λj)Δz, z+(1-λj)Δz]。
对于复杂系统时间序列实际值yj,模糊数Wij的中心参数ui和幅度εσj应满足:
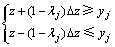 (8)
(8)
经推导,可得模糊变权重的复杂系统时间序列组合预测模型权重参数求解的数学模型:
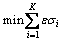 (9)
(9)
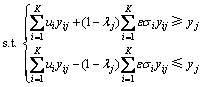
这是一个优化问题,可用自适应遗传算法进行寻优求解。自适应遗传算法的关键在于确定适应度函数,此处适应度函数选择如下:
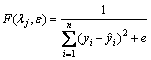 (10)
(10)
式中:e为1个很小的实数,其作用是为了防止分母为0的情况出现。
初始交叉概率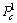 与初始变异概率
与初始变异概率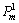 分别为:
分别为:
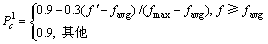 (11)
(11)
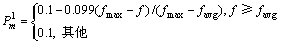 (12)
(12)
式中: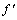 为交叉2个体较大的适应度函数值;f为个体对应的适应度函数值;favg为样本的平均适应度;fmax为样本个体的最大适应度。初始概率与变异概率随着进化代数而变化,其规律如下:
为交叉2个体较大的适应度函数值;f为个体对应的适应度函数值;favg为样本的平均适应度;fmax为样本个体的最大适应度。初始概率与变异概率随着进化代数而变化,其规律如下:
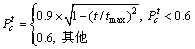 (13)
(13)
 (14)
(14)
式中:t为遗传代数;tmax为终止代数;λ为常数,此处选10。自适应遗传算法步骤如下。
Step 1: 产生初始种群P(0),代数置0,个体数目为M。
Step 2: 依次执行选择算子、交叉算子和变异算子,并计算个体的适应度。
Step 3: 对个体按适应度排序,对适应度最高的个体执行1次模糊变权重的复杂系统时间序列组合预测。
Step 4: 得到新一代种群P(t+1),代数增加1。
Step 5: 判断是否符合优化准则,若不符合,则返回Step 2;若符合,则结束。
2 基于遗传算法优化模糊变权重的复杂系统时间序列组合预测模型仿真分析
以三维非线性函数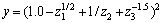 为例[14],采用本文方法进行仿真分析。使输入z1,z2和z3的取值区间均为[1,5],在此区间内产生图1所示的100个数据,其中前50个数据用作基于遗传算法优化模糊变权重的复杂系统时间序列组合预测模型的训练数据,后50个数据用作测试数据。
为例[14],采用本文方法进行仿真分析。使输入z1,z2和z3的取值区间均为[1,5],在此区间内产生图1所示的100个数据,其中前50个数据用作基于遗传算法优化模糊变权重的复杂系统时间序列组合预测模型的训练数据,后50个数据用作测试数据。
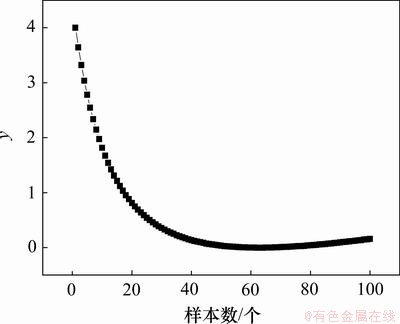
图1 三维非线性函数y仿真分析结果
Fig.1 Results of simulation analysis of 3-D nolinear function y
选用季节变量预测模型、指数回归预测模型和时变自回归滑动平均预测模型分别对前50个数据进行预测。然后,将季节变量预测模型、指数回归预测模型和时变自回归滑动平均预测模型的单个预测结果分别采用文献[8-9]中的预测方法和本文提出的预测方法进行相应训练,训练结束后,其计算值与实际值的相对误差η如图2所示。
图2表明:文献[8]中预测方法的相对误差η在-5.430 4%~5.437 9%范围内波动,文献[9]中预测方法的相对误差η在-3.369 1%~3.499 5%范围内波动,本文提出的预测方法的相对误差η在-1.994 4%~1.990 5%范围内波动。显然,与其他2种预测方法相比,本文提出的预测方法的对于前50个训练数据的训练精度较高。
选用季节变量预测模型、指数回归预测模型和时变自回归滑动平均预测模型分别对后50个数据进行预测。然后,将季节变量预测模型、指数回归预测模型和时变自回归滑动平均预测模型的单个预测结果分别采用文献[8-9]中预测方法和本文提出的预测方法进行相应测试,所得计算值与实际值的相对误差η如图3所示。从图3可见:文献[8]中预测方法的相对误差η在-5.598 1%~5.796 6%范围内波动,文献[9]中预测方法的相对误差η在-3.499 3%~3.673 6%范围内波动,本文提出的预测方法的相对误差η在-1.996 9%~1.999 7%范围内波动。显然,与其他2种预测方法相比,本文提出的基于自适应遗传算法优化的复杂系统时间序列组合预测方法的对于后50个测试数据的测试精度较高。可见:采用本文提出的基于自适应遗传算法优化的复杂系统时间序列组合预测方法,其预测精度和泛化能力上都有很大提高。
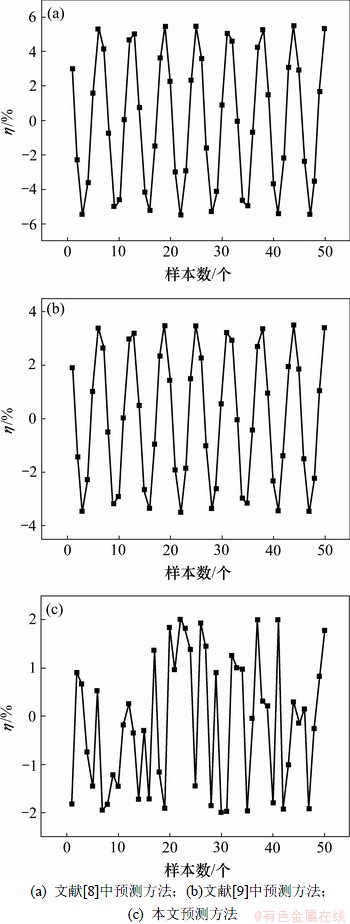
图2 不同方法所得训练数据计算值与实际值的相对误差η比较
Fig.2 Comparisons of relative error between calculated values and actual values of training data using different methods
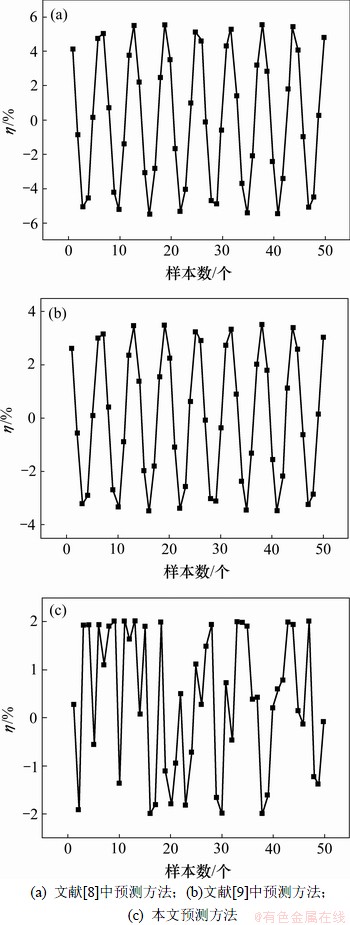
图3 测试数据预测值与实际值的相对误差η比较
Fig.3 Comparisons of relative error between forecasting and actual values of test data using different methods
3 基于遗传算法优化模糊变权重的复杂系统时间序列组合预测模型应用
自2007年长株潭(即长沙、株洲和湘潭)城市群被国务院批准为全国资源节约型和环境友好型综合配套改革实验区以来,如何从实际出发,在加快转变经济发展方式、推进经济又好又快发展的同时,有效促进经济社会发展与人口、资源、环境相协调显得十分重要。对长株潭城市群人口容量的预测不但有助于人口政策的制定,而且还对人口、资源、环境的协同发展具有一定现实意义。
自2000年以来,长株潭三市的城区人口持续增长。选用灰色系统预测模型(用F1表示)、Logistic人口预测模型(用F2表示)和Leslie矩阵预测模型(用F3表示)分别对表1所示的长株潭三市2000—2006年的城区人口为基础数据进行预测。然后,将灰色系统预测模型(F1),Logistic人口预测模型(F2)和Leslie矩阵预测模型(F3)的单个预测结果采用本文提出的模糊变权重组合预测模型(F4)进行组合预测。各种预测模型的预测结果如图4所示。
从图4可以看出:灰色系统预测模型、Logistic人口预测模型和Leslie矩阵预测模型的单个预测误差较大,且灰色系统预测模型随着预测步长的增加而显著增加。经计算得知:本文提出的基于遗传算法优化模糊变权重组合预测模型的最大相对误差为2.89%,灰色系统预测模型的最大相对误差为5.94%,Logistic人口预测模型的最大相对误差为4.87%,Leslie矩阵预测模型的最大相对误差为3.24%。可见:本文提出的基于遗传算法优化模糊变权重组合预测模型能综合各预测方法的优点,能更好地拟合历史数据。
表1 长株潭人口规模
Table 1 Population capacity of Chang—Zhu—Tan city 万人
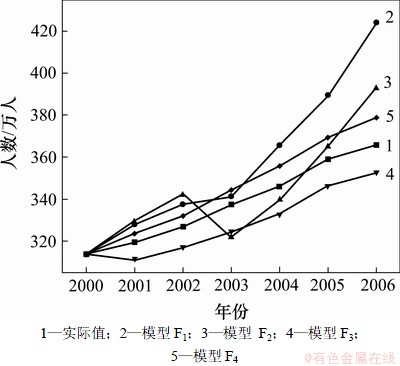
图4 长株潭人口规模历史数据与预测值比较
Fig.4 Comparison of history datum of city population of Chang—Zhu—Tan with forecasting values using different models
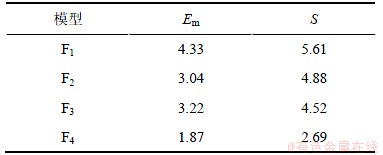
与本文提出的基于遗传算法优化模糊变权重组合预测模型的预测精度相比,灰色系统预测模型、Logistic人口预测模型和Leslie矩阵预测模型的预测精度较低,而本文提出的基于遗传算法优化模糊变权重组合预测模型的预测平均误差(Em)和预测平方根S误差均较小,如表2所示。
表2 本文预测方法与其它预测方法的误差比较
Table 2 Error of forecasting method in the paper in comparison with those of other forecasting methods
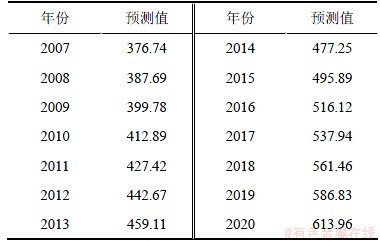
基于长株潭三市2000—2006年的城区人口为基础数据,采用本文提出的基于遗传算法优化模糊变权重组合预测模型预测2007—2020年长株潭三市的城区人口规模,其预测结果如表3所示。
根据《长株潭城市群区域规划(2004—2020)》,到2020年长株潭三市城区人口控制在(610~630)万人之间,这与2020年的预测值613.96万人是一致的,说明本文提出的基于遗传算法优化模糊变权重组合预测模型达到了预测的目的。
表3 长株潭人口规模预测值
Table 3 Population forecasting value of Chang-Zhu-Tan city 万人
4 结论
(1) 将复杂系统时间序列组合预测模型的权系数视为模糊数,利用自适应遗传算法优化复杂系统时间序列组合预测模型的权重系数,建立了基于自适应遗传算法优化的复杂系统时间序列组合预测模型。
(2) 此组合预测平均误差和预测平方根误差均较小。该预测模型建模数据少,计算简便,预测结果精度较高,方法简便,易于实际应用,具有广泛的适用性,为复杂系统时间序列合理、准确预测提供了新思路。
(3) 所提出的基于自适应遗传算法优化的复杂系统时间序列组合预测模型的最大相对误差为2.89%,小于各预测模型中最小的最大相对误差3.24%。这表明所提出的基于自适应遗传算法优化的复杂系统时间序列组合预测模型能综合各预测方法的优点,可更好地拟合历史数据。
参考文献:
[1] Hinich M J, Foster J, Wild P. Structural change in macroeconomic time series: A complex systems perspective[J]. Journal of Macroeconomics, 2006, 28(1): 136-150.
[2] Koulouriotis D E, Diakoulakis I E, Emiris D M, et al. Development of dynamic cognitive networks as complex systems approximators: Validation in financial time series[J]. Applied Soft Computing, 2005, 5(2): 157-179.
[3] E Jiaqiang, LI Yuqiang, GONG Jinke. Function chain neural network prediction on heat transfer performance of oscillating heat pipe based on grey relational analysis[J]. Journal of Central South University of Technology, 2011, 18(5): 1733-1737.
[4] LI Wenyuan, XU Min, ZHOU Xianghong. Jasmine. Unraveling complex temporal associations in cellular systems across multiple time-series microarray datasets[J]. Journal of Biomedical Informatics, 2010, 43(4): 550-559.
[5] Azadeh A, Saberi M, Jiryaei Z. An intelligent decision support system for forecasting and optimization of complex personnel attributes in a large bank[J]. Expert Systems with Applications, 2012, 39(16): 12358-12370.
[6]  J M, et al. Influence of forecasting electricity prices in the optimization of complex hydrothermal systems[J]. Journal of Computational and Applied Mathematics, 2009, 232(2): 262-274.
J M, et al. Influence of forecasting electricity prices in the optimization of complex hydrothermal systems[J]. Journal of Computational and Applied Mathematics, 2009, 232(2): 262-274.
[7] Bates J M, Granger C W J. Combination of forecasts[J]. Operations Research Quarterly, 1969, 20(4): 451-468.
[8] 李学全, 李春生. 一种改进的模糊变权重组合预测方法[J]. 中南工业大学学报: 自然科学版, 2003, 34(6): 708-710.
LI Xuequan, LI Chunsheng. An improved method of fuzzy variable weight combination forecasting[J]. Journal of Central South University of Technology: Natural Science Edition, 2003, 34(6): 708-710.
[9] 鄂加强, 王耀南, 龚金科. 一种新的非线性模糊自适应变权重组合预测模型[J]. 模糊系统与数学, 2006, 20(4): 123-127.
E Jiaqiang, WANG Yaonan, GONG Jinke. A new nonlinear combined forecasting model based on method of fuzzy adaptive variable weight[J]. Fuzzy Sets and Systems, 2006, 20(4): 123-127.
[10] YAO Ye, LIAN Zhiwei, LIU Shiqing, et al. Hourly cooling load prediction by a combined forecasting model based on analytic hierarchy process[J]. International Journal of Thermal Sciences, 2004, 43(11): 1107-1118.
[11] TAN Zhongfu, ZHANG Jinliang, WANG Jianhui, et al. Day-ahead electricity price forecasting using wavelet transform combined with ARIMA and GARCH models[J]. Applied Energy, 2010, 87(11): 3606-3610.
[12] Unsihuay-Vila C, Zambroni de Souza A C, Marangon-Lima J W, et al. Electricity demand and spot price forecasting using evolutionary computation combined with chaotic nonlinear dynamic model[J]. International Journal of Electrical Power & Energy Systems, 2010, 32(2): 108-116.
[13] 鄂加强, 左红艳, 罗周全. 神经网络模糊推理智能信息融合及其工程应用[M]. 北京: 中国水利水电出版社, 2012: 1-30.
E Jiaqiang, ZUO Hongyan, LUO Zhouquan. Fuzzy inference neural network intelligent information fusion and its engineering application[M]. Beijing: China Water Power Press, 2012: 1-30.
[14] 罗周全, 左红艳, 王爽英, 等. 基于模糊自适应变权重算法的函数链神经网络预测方法[J]. 中南大学学报:自然科学版, 2011, 42(9): 2812-2818.
LUO Zhouquan, ZUO Hongyan, WANG Shuangying, et al. Functional link neural network forecasting method based on fuzzy adaptive variable weight algorithm[J]. Journal of Central South University: Natural Science Edition, 2011, 42(9): 2812-2818.
(编辑 陈灿华)
收稿日期:2013-02-28;修回日期:2013-04-27
基金项目:国家自然科学基金资助项目(70971036)
通信作者:单汨源(1962-),男,湖南平江人,博士,教授,博士生导师,从事城市化人口发展机理及其预测研究;电话:13397519988;E-mail: shanmiyuan@163.com