DOI: 10.11817/j.ysxb.1004.0609.2020-37553
基于DISL方法的硬岩矿柱脆性破坏数值模拟
刘 建1, 2，赵国彦2，胡静云1
(1. 长沙矿山研究院有限责任公司 金属矿山安全技术国家重点实验室，长沙 410012;
2. 中南大学 资源与安全工程学院，长沙 410083)
摘 要：以板裂为表现形式的岩石脆性破坏行为是深埋硬岩岩体开挖卸荷造成的典型围岩破坏现象。在简要比较4种硬岩脆性破坏数值模拟方法的基础上，基于损伤启裂-板裂界限(Damage initiation and spalling limit, DISL)模型，借助FLAC3D开展硬岩矿柱原位压缩及单轴压缩数值模拟，探讨DISL方法的适用性并进一步探究硬岩矿柱的脆性破坏过程及其特征。结果表明：原位压缩模拟中，当卸荷总时步大于某一临界数值时，矿柱两侧发生V形破坏，进而矿柱整体形成沙漏状；不同均质度下屈服破坏单元主要分布在V形破坏区内及周围，其分布范围受低围压区及张拉区范围的控制；V形剪切带主要以拉剪破坏为主，剪切带内部靠近矿柱边壁一侧，伴有张拉破坏单元；单轴压缩模拟中，峰后阶段矿柱两侧仍然产生V形破坏，并且张拉裂隙的形成范围受剪切带控制。
关键词：硬岩矿柱；脆性破坏；数值模拟；DISL方法；破坏模式；强度特征
文章编号：1004-0609(2020)-03-0684-14 中图分类号：TD322 文献标志码：A
以板裂(Spalling and slabbing)为表现形式的岩石渐进式破坏行为不仅出现在以隧洞、井巷为代表的高应力硬岩地下开挖边界面处，同时也发生在高应力硬岩矿柱周边。PRITCHARD等[1]在加拿大Elliot Lake矿区观测到详细的硬岩矿柱渐进式破坏过程，矿柱表面逐渐剥落成沙漏状，最终发生压剪破坏；PERRAS[2]同样在Gonzen矿观测到板状岩块从矿柱边壁逐渐剥落的现象；LUNDER等[3]针对178例硬岩矿柱破坏模式的现场案例统计研究表明，当硬岩矿柱的宽高比小于2.5时，其主导破坏模式为渐进的板裂化与剥落破坏，最终形成类似沙漏状的破坏形状，如图1所示[2-3]。这种新的破坏形式本质上是一种与延伸劈裂裂隙有关的张拉破坏过程，剥落破坏岩板平行于围岩边界面[4]，目前已有的研究成果通常称此类破坏为脆性破坏(Brittle failure)[5]，国内部分学者直接根据该类破坏的表现形式称之为板裂破坏[4,6]。从破坏形态来看，高应力硬岩脆性破坏通常导致地下隧洞或巷道边壁围岩最大主应力处形成V形槽(V-shaped notches)，而对硬岩矿柱来说，则会导致其成为沙漏形。从破坏强度来看，则表现出一种更值得岩石力学工作者探究的强度矛盾性。
进行地下开挖工程稳定性分析首先需要确定原位岩体强度。经验的Hoek-Brown强度准则通常利用岩体质量分级值RMR或地质强度指标值GSI对实验室获得的岩石强度参数(mi、s、a和σc)进行弱化。而对于较完整硬岩(一般mi或UCS/σt≥15，GSI≥65[7]或RMR≥70[8])，经弱化后获得的上述岩体强度参数与实验室获得的完整岩石强度参数十分接近，这就意味着现场岩体的强度与完整岩石的强度相差不多[8]。但是，实际的工程实例表明，即使对于完整硬岩，通过地下开挖工程反分析获得的原位岩体强度依然低于实验室完整岩石强度的一半，如PELLI等[9]、MARTIN等[10]。STACEY等[11]、WAGNER[12]、CASTRO等[13]和DIEDERICHS[14]通过脆性破坏反分析均得出当隧洞周边应力超过0.3σc~0.5σc(室内岩样裂纹起裂应力)就会引起脆性破坏，并且该过程与围压无关。WESSELOO等[15]直接指出，岩石及岩体的复杂力学行为长期困扰岩土工程师的主要问题之一就是高强度岩体在低应力条件下的损伤破裂现象。
通过对加拿大Quirke矿山硬岩矿柱(该矿山同样位于Elliot Lake矿区，mi=22，GSI为77~85[16])反分析，RAFIEI等[17]发现矿柱平均强度与矿柱岩体完整岩石单轴抗压强度之比为0.33。针对MARTIN等[18]提及的6个硬岩矿柱强度公式，临界尺寸矿柱强度(尺寸为1 m×2 m，LUNDER等[3]指出对于边长大于1~1.5 m的矿柱，其强度因尺寸增加而降低的幅度可以忽略)与完整岩石强度之比介于0.21~0.44，平均为0.31。上述结果表明，硬岩矿柱脆性破坏时同样表现出类似的强度矛盾性。
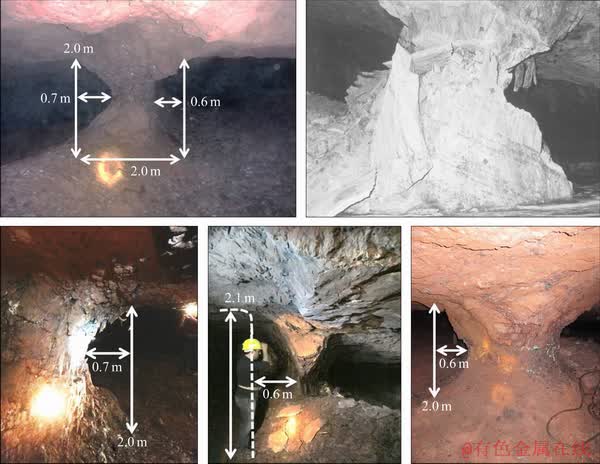
图1 硬岩矿柱脆性破坏[2-3]
Fig. 1 Observations of hard rock pillars brittle failure[2-3]
以MARTIN[8]、KAISER等[16]、DIEDERICHS[19]为代表的加拿大学者通过对Mine-by(AECL’s URL)实验隧洞系统研究之后得出：低围压下高应力硬岩的原位强度就是室内岩样的裂纹起裂强度，即UCSfield为0.3σc~0.5σc=σci。上述结论是目前硬岩脆性破坏的主要观点，具体含义：张拉裂纹起裂是结晶类硬岩在压缩荷载作用下的主要损伤破坏形式(张性破裂)，在低围压下，当外部载荷达到裂纹起裂强度，岩石内部张拉裂纹起裂并沿最大主应力方向扩展(亚临界裂纹扩展)就会导致类似于板裂、层裂的脆性破坏形式，同时岩体非均质性、爆破振动、开挖扰动、自由边界效应、隧洞开挖过程中应力旋转效应等作用对裂纹扩展的影响不可忽略[6]。区别于高围压条件下的剪切破坏，无论采用传统的弹性模型、理想弹塑性模型，还是采用HOEK等[20]提出的弹脆性形模型，均无法准确预测地下开挖围岩的破坏范围和深度[5,8]。基于此，MARTIN等[10]提出了m=0 & s=0.11方法，HAJIABDOLMAJI等[5]提出了内聚力弱化-摩擦力强化(Cohesion weakening and frictional strengthening, CWFS)方法，DIEDERICHS[19]提出了损伤启裂-板裂界限(Damage initiation and spalling limit, DISL)方法。
然而，国内外学者大多关注地下隧洞或巷道的脆性破坏，鲜少有学者关注高应力硬岩矿柱的脆性破坏过程，上述方法是否仍能捕捉硬岩矿柱的沙漏形破坏模式(如图1所示)仍有待进一步验证。本文在简要总结、比较几种硬岩脆性破坏数值模拟方法的基础上，根据比较结果，基于DISL模型，并同时考虑矿柱周围采场的开挖卸荷速率及矿柱岩体的不均质性，借助FLAC3D模拟硬岩矿柱的破坏过程，一方面探讨DISL方法的适用性，另一方面探究硬岩矿柱的脆性破坏过程及其特征。
1 硬岩脆性破坏数值模型
1.1 Stacey张拉应变方法(1981)
在压缩荷载作用下岩石内部可以产生轴向张拉破裂，这一观点已经得到国内外众多学者证实，如单轴压缩岩样的劈裂破坏[4, 14, 21]、FAIRHURST等[22]描述的地下巷道或硐室边壁围岩的剥落破坏(Slabbing)等。HALBAUER等[23]通过对加载卸荷岩样进行切片观察发现切片内部破裂基本沿最大主应力方向。鉴于上述现象，STACEY[24]于1981年提出一种基于最大张拉应变(Extension strain)的脆性岩石起裂准则，该准则认为当岩石内部最大拉应变超过某一限值时岩石将会开裂，可表示为
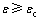(1)
式中：εc表示岩石最大张拉应变阀值。
STACEY[24]将该阀值定义为室内岩样单轴和三轴压缩侧向应变发生突变的点，即当岩石内部发生轴向张拉破裂时，侧向应变会发生突增，并同时给出了16种岩石的张拉应变阀值，在单轴压缩试验中与其对应的应力水平大致为0.3σc(σc为岩石单轴抗压强度)。本质上，Stacey定义的临界张拉应变就是裂纹起裂应力对应的侧向应变(称之为裂纹起裂应变)[25]。LI等[26]发现在巴西劈裂实验中当试样中部侧向应变达到裂纹起裂应变时岩样开始发生轴向劈裂。在压缩荷载作用下，张拉破裂沿最大主应力方向延伸，沿最小主应力方向开裂，对于理想的线弹性材料，沿最小主应力方向的应变为(压为正)
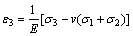(2)
式中：E为弹性模量；v为泊松比；ε3为第三主应变；
σ1、σ2、σ3分别为第一、第二、第三主应力。对于脆性硬岩，破坏前基本以弹性变形为主，进而式(1)可改写为
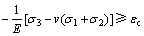(3)
DOWDING等[27]通过分析5个典型的围岩板裂化破坏与岩爆案例得出隧洞开挖引起的洞壁围岩最大切向应力与室内岩石单轴抗压强度之比达到0.35时，便会导致围岩产生板裂化破坏现象。以当前观点来看，DOWDING等[27]分析得出的原位岩体强度实际上就是室内岩样的裂纹起裂强度。STACEY[24]提出的张拉应变准则与DOWDING等[27]提出的经验判据是对同一状态的不同角度描述，前者为应变判据，后者为应力判据，前者的张拉应变阀值对应于后者的板裂破坏临界应力。近来，WESSELOO等[15]又对该准则进行了发展，使其成为三轴拉伸(σ2接近σ1)情况下的破坏准则。本文作者采用上述方法，同时参考STACEY[24]给出的张拉应变阀值(7.3×105~17.5×105)模拟Mine-by实验隧洞的V形破坏，采用弹性分析，并以式(3)作为围岩起裂判据，几乎全部模型区域都属于开裂区，这与临界张拉应变过低有关。图2所示为不同εc时Mine-by实验隧洞的模拟结果(图中红色区域表示开裂区)。
图3所示为Mine-by实验隧洞的实际破坏情况及传统本构模型的模拟结果，V形破坏深度为0.53 m，破坏范围为64°。图2(d)中模拟破裂区深度为0.22 m，破坏范围为84°，随临界张拉应变值εc增大，破裂区深度及范围将继续减小。即便在不考虑εc真实值的情况下，Stacey张拉应变方法的模拟效果依然较差。
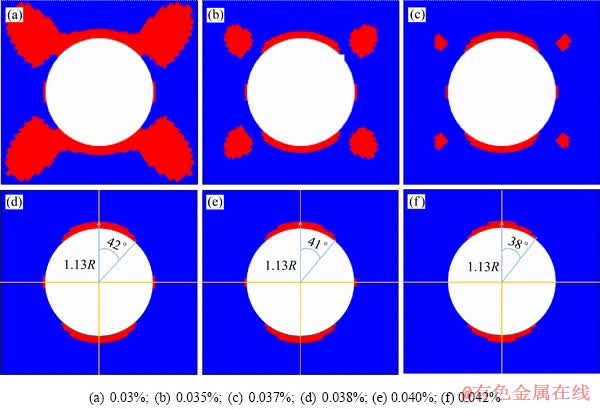
图2 不同εc时Mine-by实验隧洞的数值模拟结果
Fig. 2 Numerical simulation results of Mine-by test tunnel under different εc
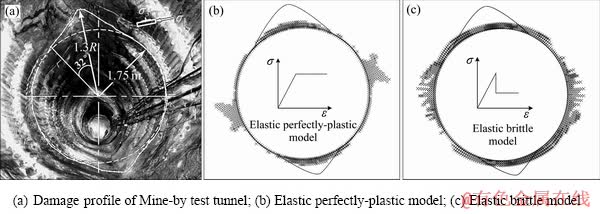
图3 Mine-by实验隧洞V形破坏示意图及传统模型的模拟结果[5, 19]
Fig. 3 V-shaped notches of Mine-by test tunnel and numerical results based on traditional constitutive models[5, 19]
1.2 Hoek-Brown脆性参数方法(1999)
通过详细观察Mine-by实验隧洞及其它隧洞案例V形破坏的形成过程发现破坏区内剥落岩板主要沿边壁形成，破裂方向垂直于最小主应力方向，这表明破坏区内主要发生张拉破裂[10, 28]。结合STACEY[24]提出的张拉应变准则及Mine-by实验隧洞V形破坏区内的张拉破裂模式可以推知以Spalling、Slabbing及劈裂为代表的脆性破坏过程主要受岩石内聚力控制，与岩石内部摩擦力无关。MARTIN等[29]通过一系列损伤控制的循环加卸载实验发现岩样内部累计的张拉破裂对岩样内聚力具有弱化作用，并且这种弱化作用在达到峰值强度之前就已经发生；他们进一步的研究表明岩样破裂过程中内聚力和由内摩擦角引起的内摩擦力并非同时发挥作用，而是在内聚力大致降低70%以后内摩擦力才会全部启动。基于Mine-by实验隧洞的微震监测结果，MARTIN等[10]指出原位岩体损伤(Damage- initiation)初始应力可以表示为一个常量偏应力的形式
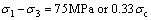(4)
式中：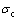
为Mine-by实验隧洞围岩Lac du Bonnet花岗岩的单轴抗压强度，其值为224 MPa[5]。上式可以表示为霍克-布朗强度公式形式
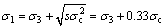(5)
式中：m等于0以反映内摩擦力没有启动(从摩尔-库伦强度准则角度看，内摩擦角φ=0，内聚力c=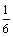
σc，也反映出内摩擦力没有发挥作用)，s=0.11。上式隐含
表明由压应力引起的脆性破裂过程主要受内聚力弱化控制(张拉破裂发展、集聚导致内聚力弱化)，与内摩擦力无关。
关于该方法有3点需要注意：1) MARTIN等[10]指出应用m=0 & s=0.11方法时应以弹性分析为基础，进而采用公式(5)作为岩石破裂判断准则；2) m=0 & s=0.11方法仅适用于应力引起的脆性破坏(压应力引起的张拉破坏)，而对直接拉伸破坏无效，因为它会高估岩体的抗拉强度。3) SUORINENI等[30]指出内聚力参数s值随岩石种类变化，并非为固定值0.11，因此，应用s=0.11进行分析有时会高估脆性破坏的程度，SUORINENI等[30]同时提出了针对不同岩石的s的确定方法。
借助FLAC3D，应用m=0 & s=0.11方法模拟Mine-by实验隧洞的V形破坏，结果如图4(a)所示，图4(b)为g=σ1-σ3-0.33σc的等值线分布图。模拟结果中，破裂区深度为0.67 m，破坏范围为76°，显然该方法会高估破裂区深度及范围，并且破裂区形状也与实际破坏形态存在差异。
1.3 CWFS方法(2002)
常用的摩尔-库伦强度准则和霍克-布朗强度准则均假定组成岩土材料抗剪强度的内聚力和内摩擦力随材料变形同时发挥作用。然而，SCHMERTMANN等[31]的研究结果表明在土体材料中内聚力和内摩擦力并非同时启动，内聚力总是先于内摩擦力达到最大值。MARTIN等[29]通过Lac du Bonnet花岗岩循环加卸载实验发现压缩荷载作用下岩样内聚力随塑性变形逐渐减小，内摩擦角随塑性变形逐渐增大。同时，工程现场中高应力硬岩的板裂破坏形式也表明岩体强度中内聚力占主导。基于上述学者的研究成果，HAJIABDOLMAJID等[5]提出了CWFS方法，如图5所示。CWFS模型是一种以弹塑性理论为基础的脆性破坏模型，以塑性区表征高应力破裂区，借助FLAC2/3D的应变软化模型可以实现。
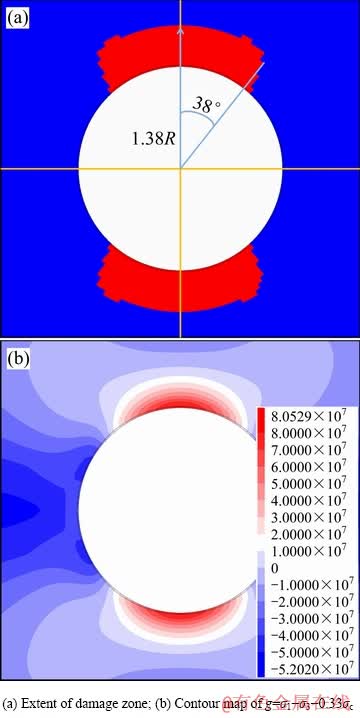
图4 基于m=0 & s=0.11方法的数值模拟结果
Fig. 4 Numerical results based on m=0 & s=0.11 method
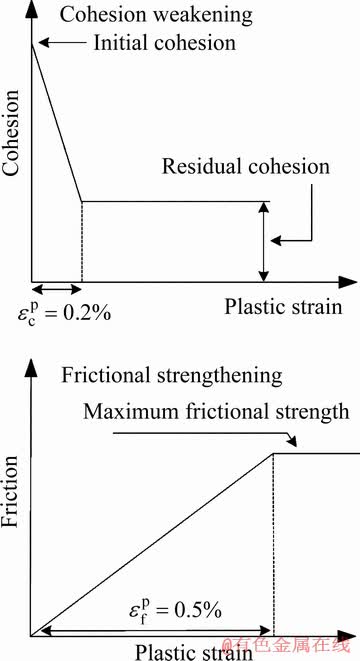
图5 CWFS方法示意图[5]
Fig. 5 Illustration of CWFS method[5]
与应变软化模型不同的是，CWFS方法中初始内摩擦角随单元塑性剪切应变发展会逐渐增大，内聚力则逐渐减小，该过程反映的是脆性硬岩破坏过程中内聚力的丧失和内摩擦力的启动。最近，WALTON等[32]针对Indiana石灰岩和Carrara大理岩做了大量不同围压下的循环加卸载实验，验证了MARTIN等[29]结论的正确性。此外，关于CWFS模型的参数取值仍需进一步探讨，HAJIABDOLMAJID等[5]在针对Mine-by实验隧洞进行模拟时，将初始内摩擦角设为0，残余内摩擦角设为峰值强度时的摩擦角，具有一定的道理，然而关于其他参数的取值则带有一定的经验色彩。运用HAJIABDOLMAJID等[5]提供的参数，借助FLAC3D针对Mine-by实验隧洞进行模拟，结果如图6所示，模拟V形破坏深度为0.75 m，破坏范围为74°，相对误差之和为59%。该方法显然会高估V形破坏深度，但破坏范围比较接近。
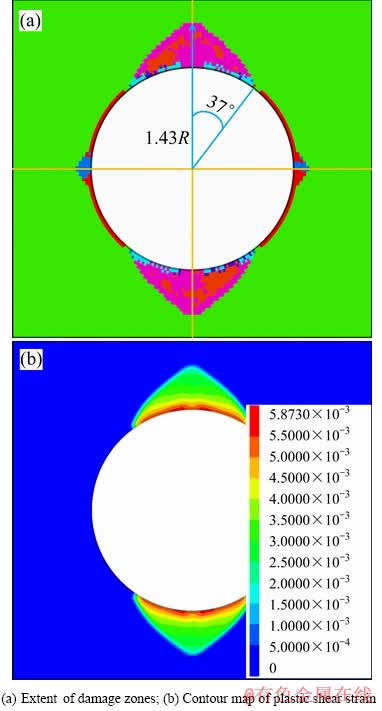
图6 基于CWFS方法的数值模拟结果
Fig. 6 Numerical results based on CWFS method
1.4 DISL方法(2007)
Mine-by实验隧洞[8]的监测结果及PELLI等[9]、STACEY等[11]、MARTIN[8]、KAISER等[16]的研究结果均表明，低围压下脆性硬岩的原位强度就是(或处于同一水平)室内岩样的裂纹起裂强度。DIEDERICHS[19]在此基础上又提出高围压下脆性硬岩的原位强度就是室内岩样的裂纹损伤强度。随围压增高，张拉裂纹扩展受到抑制，脆性硬岩将由张拉破坏模式过渡到剪切破坏模式。DIEDERICHS[19]进而提出了DISL方法，同时提出了该方法的参数取值方法并对其应用范围进行了界定[33]。与CWFS方法相同，DISL方法也是以弹塑性理论为基础的脆性破坏模型，同样以塑性区表征高应力破裂区，可借助弹塑性有限元软件Phase2实现，同时也可利用FLAC2/3D进行实现。图7所示为采用该方法模拟Mine-by实验隧洞V形破坏的Phase2及FLAC2/3D模型参数，基于FLAC3D的数值模拟结果如图8所示。模拟结果中，V形破坏深度为0.46 m，破坏范围为52°，相对误差之和为32%，破裂区形状与实际较为接近。
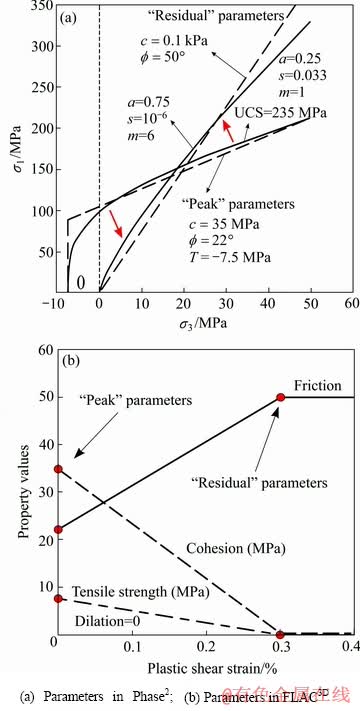
图7 Mine-by实验隧道V形破坏的DISL方法模型参数[19]
Fig. 7 Strength parameters of V-shaped notches of Mine-by test tunnel by DISL method[19]
虽然DISL方法通过FLAC2/3D的实现方式与CWFS方法相似，但其是在深刻认识脆性硬岩压缩—张拉损伤机制的基础上结合室内岩样全应力应变曲线峰前阶段与裂纹起裂、裂纹扩展相关的两个关键特征应力提出的，与CWFS方法相比，DISL方法参数更加明确。此外，EDELBRO[34-35]基于CWFS模型和DISL模型又提出了内聚力软化-摩擦角硬化(Cohesion softening and friction hardening, CSFH)模型，但是其本质还是DISL模型，EDELBRO[34-35]仅仅改变了“峰值”强度及“残余”强度参数的取值。CSFH方法同样借助弹塑性有限元软件Phase2进行实现。DISL方法的本质是借助霍克-布朗准则或摩尔-库伦准则根据围压不同将强度曲线分段表示，并同时考虑由低围压过渡到高围压的板裂界限(Spalling limit)。鉴于此，最近KAISER等[36]直接提出了一个S形的强度准则用以描述脆性硬岩在不同围压时不同破坏模式下的强度。
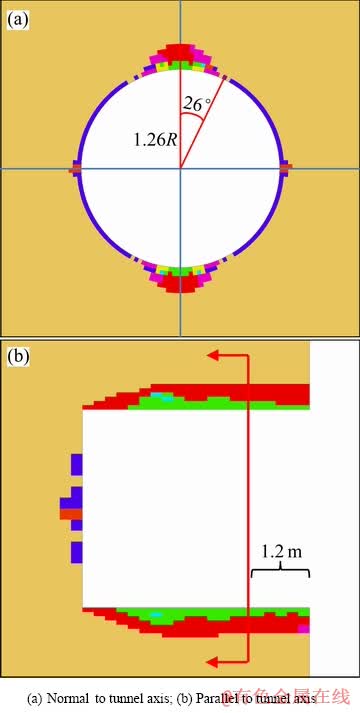
图8 基于DISL方法的数值模拟结果
Fig. 8 Numerical results based on DISL method
2 硬岩矿柱脆性破坏数值模拟
从上述4种方法的模拟效果来看，CWFS法和DISL法的模拟结果与Mine-by实验隧洞的实际破裂情况较为接近，而且从破坏深度及破坏范围的联合相对误差角度看DISL方法的结果更好。因此，本节采用DISL方法模拟硬岩矿柱的脆性破坏过程，数值模拟思路如图9(a)所示。
2.1 模型构建
计算模型如图9(b)所示，采用平面应变模型，矿柱尺寸为4 m×4 m，采场尺寸为4 m×4 m，矿柱、采场及顶底板围岩的单元尺寸均为0.1 m×0.1 m，边界条件及初始条件为：固定模型y方向的变形，固定模型底部x、y、z方向的位移及两侧x方向的位移。在模型顶部施加应力边界条件，同时在模型内部设置初始应力场(不考虑应力梯度)。边界条件及初始应力施加完毕后模型自动保持平衡，然后对采场进行开挖，应力重分布过程中矿柱荷载逐渐增加直至矿柱最终破坏。
仍采用Mine-by实验隧洞洞壁围岩的物理力学参数，内聚力、内摩擦角、抗拉强度、剪胀角、塑性剪切应变阀值参见图7，岩体单轴抗压强度为235 MPa，弹性模量为60 GPa，泊松比为0.2。原岩初始应力场为σ1=60 MPa、σ2=45 MPa、σ3=11 MPa，上述应力场与Mine-by实验隧洞所处的应力场环境大小相同，方向有异(见图3)，最大主应力方向竖直向下更符合地下矿山矿柱的承载特点。采用上述力学参数及初始应力场的理由：一方面是参数可信度高，尤其是力学参数，经过Mine-by实验隧洞V形破坏数值模拟的验证，模拟结果与实际结果比较契合；另一方面，与Mine-by实验隧洞的数值模型相比，岩体力学参数、初始应力场(数值)及外部边界条件相同，而仅仅内部开挖边界条件有异，更能凸显脆性破坏数值模型本身的特点。
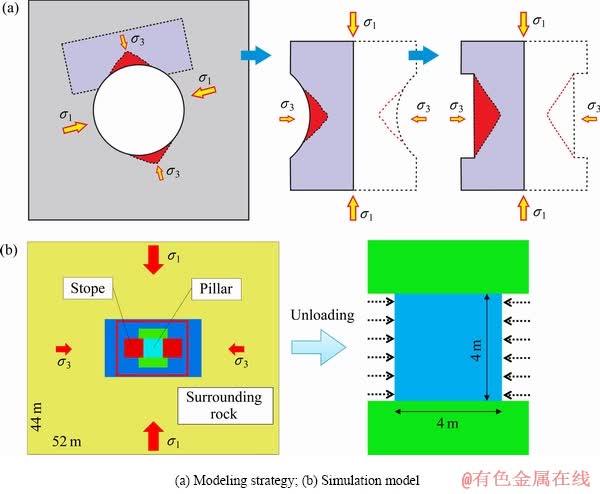
图9 数值模拟思路及计算模型
Fig. 9 Modeling strategy and numerical simulation model
对采场施加开挖命令后(Model null)，直接在采场边界施加与边界法向初始应力相同的内部应力边界条件，以使模型依然保持平衡状态，然后随时步(Step)进行线性降低施加的边界应力，进而模拟工程实际中的开挖卸荷过程。在FLAC3D中，模拟开挖卸荷需自定义一个relax函数并配合apply命令及hist关键字联合使用[37]：
define relax
if step < ncyc then
relax=1.0 - (float(step)/float(ncyc))
else
relax = 0
end_if
end
set @ncyc = 2000 ; 卸荷时步
2.2 岩体非均匀性
岩石是一种典型的非均质材料。目前，在连续介质框架内考虑岩石介质非均匀性的主流方法是利用某种统计分布函数在细观尺度下描述岩石材料的物理力学特性[38-39]，其中，最常用的分布类型是Weibull分布。参照文献[38]及[40]，本文采用Weibull分布描述矿柱单元弹性模量及单轴抗压强度的空间变异性。Weibull分布的概率密度函数为
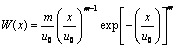(6)
式中：x表示单元力学参数；u0为比例参数，m为形状参数且m＞1。不同形状参数m下，Weibull分布的形状如图10所示(图中u0=60)，形状参数m越大，x的分布越集中，故m是反映材料内部结构均质度的参数。m越大，材料越趋于各向同性；m越小，材料内部各点的差异则越大。
图11所示为DISL方法对应的强度包络线。上文提到，低围压下脆性硬岩的原位强度就是(或处于同一水平)室内岩样的裂纹起裂强度。此时岩体强度主要由内聚力提供，而内摩擦力尚未发挥作用，由此推出c为0.15σc~0.25σc(也可从式(5)导出c=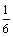σc)，即初始内聚力与单轴抗压强度具有简单的线性关系[41]。初始内摩擦角与残余内摩擦角保持不变。此外，同时假定单元单轴抗拉强度和塑性剪切应变阀值正比于单元单轴抗压强度。
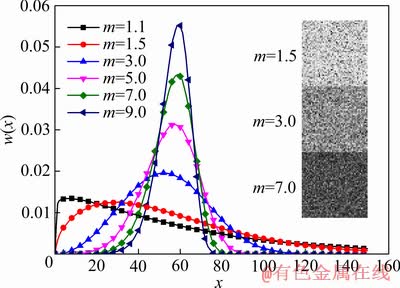
图10 不同形状参数下Weibull分布概率密度函数曲线
Fig. 10 Curves of Weibull distribution with different shape factors
2.3 结果分析
图12所示为均匀矿柱在不同卸荷速率下的破坏模式，卸荷速率分别为①瞬间卸荷、②100步卸荷、③500步卸荷、④1000步卸荷、⑤2000步卸荷、⑥3000步卸荷。分图题中同时给出了达到相应的破坏模式所需的时步数。由图12可知，当卸荷时步大于500时，矿柱两侧均能发展成V形破坏进而矿柱整体形成如图1所示的沙漏状，V形破坏深度为1.5m，与矿柱尺寸之比为0.375，这与图1中的方形矿柱破坏情况十分相似(0.35)。而当卸荷时步小于100时，矿柱顶部的剪切带一直向下发展并发生了偏转，这可能是卸荷速率过快，矿柱内局部不平衡力变化加剧，造成剪切带不稳定发展。可以推知，在100时步及500时步之间存在一临界卸荷时步值，其是两种破坏模式的分界点。
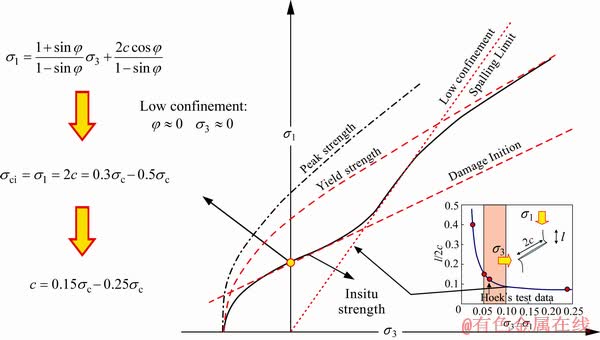
图11 初始内聚力与单轴抗压强度的关系[19, 36, 41]
Fig. 11 Relationship between initial cohesion and uniaxial compressive strength in DISL method[19, 36, 41]
图13所示为2000时步卸荷速率时，均匀矿柱及非均匀矿柱的破坏过程(H表示均匀矿柱)，不均质度参数m分别为7、10、15。由图13可知，不同均质度参数下矿柱整体均能发展成沙漏状，V形剪切带靠近矿柱边壁一侧均出现张拉屈服单元。与均匀矿柱不同的是，每一时步下(1700，2000)非均质矿柱V形破坏区范围内均会出现屈服单元(以剪切屈服单元为主)，并且随时步进行逐步向矿柱中间发展，表现出一种渐进破坏特性。矿柱均质度越低，V形破坏区内部及周围屈服的单元数量越多，但矿柱顶部与底部锥形区域内屈服的单元数量较少。图14所示为均匀矿柱在1700、2000、2300时步下最小主应力及最大主应力的分布云图。1700时步时矿柱两侧已出现一定范围的低围压区(0~5 MPa)，其形状大致呈现出扁平V形，随开挖卸荷进行低围压区逐渐向矿柱内部扩展，其形状也越来越接近V形破坏区。2300时步时，矿柱两侧已出现明显的张拉区域(灰色区域)，此时低围压区与V形破坏区更加契合。反观矿柱顶部及底部的锥形区域内，最小主应力随时步进行逐渐增大，且其量值明显比相应时步下矿柱两侧的最小主应力大。综合上述分析可知，不均匀矿柱V形破坏区范围内出现屈服单元是低围压下的压剪破坏及张拉剪切破坏造成的，在低围压下及拉应力条件下，矿柱两侧岩体的强度较低，从而导致在卸荷加载过程中，矿柱两侧首先出现屈服单元，且屈服单元出现的范围受低围压区及张拉区范围的控制。
图15所示为截至到2300时步为止均匀矿柱V形剪切带单元的初始屈服状态(首次屈服)及应力状态和监测单元的应力路径。由图15可知，V形剪切带自内向外依次为压剪破坏、拉剪破坏、张拉破坏，并且拉剪破坏单元明显多于压剪破坏单元，V形剪切带的主体部分以拉剪破坏单元为主。经过统计，2300时步时矿柱中张拉屈服单元数量为59，拉剪屈服单元数量为180，压剪屈服单元数量为112。周辉等[42]指出深部岩体工程中张拉剪切破坏是洞壁围岩的主要破坏机制，上述模拟结果与周辉等[42]的认识相契合。随着开挖卸荷不断进行，剪切带单元的初始应力路径趋势大致为最大主应力加荷最小主应力卸荷，到某一时步以后，张拉破坏单元的应力路径发生明显偏转直至最终破坏。这可能是剪切带形成后V形破裂区最大主应力逐渐释放所引起。
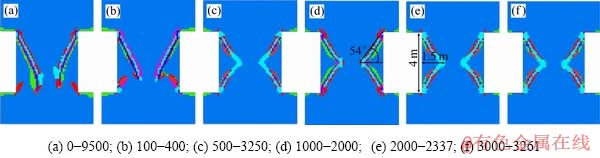
图12 不同卸荷速率下矿柱的破坏模式
Fig. 12 Failure modes of hard rock pillars under different unloading rates
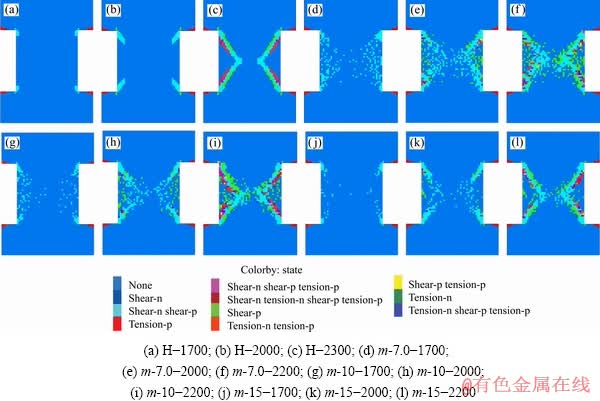
图13 不同均质度下矿柱的破坏过程
Fig. 13 Failure process of pillars with different heterogeneities
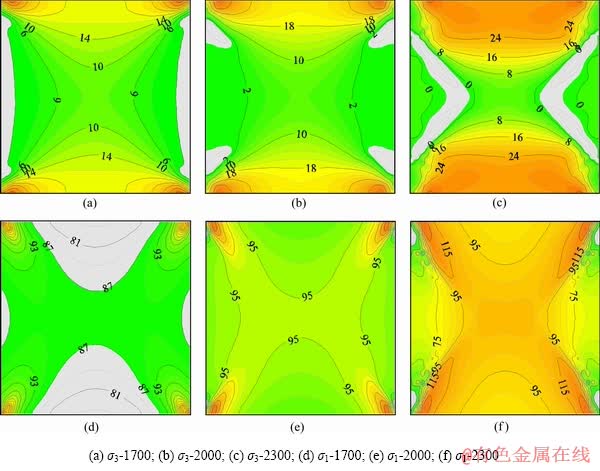
图14 不同时步下σ3和σ1的分布云图
Fig. 14 Contour maps of σ3 and σ1 under different steps
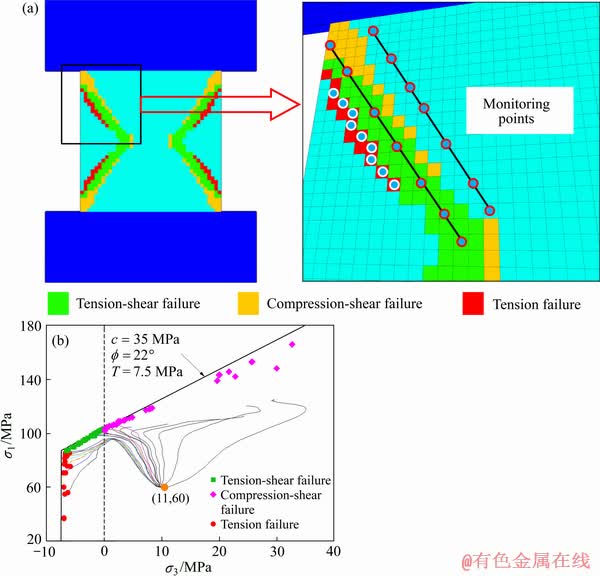
图15 均匀矿柱剪切带单元的初始屈服状态、应力状态以及监测单元的应力路径
Fig. 15 Initial yield state of shear band zones(a) and stress state of yield zones and stress paths of monitoring points(b) of homogeneous pillar
2.4 矿柱单轴压缩
为探究图9中硬岩矿柱脆性破坏时的强度特性，构建如图16所示的矿柱单轴压缩数值模型。矿柱尺寸保持不变，顶底板高度均为28 m，矿柱及围岩的单元尺寸均为0.1 m×0.1 m。固定模型y方向的变形，固定模型两侧x方向的位移及模型底部z方向的位移，同时在模型顶部施加速度边界条件，加载速率为1×10-6 m/步。计算过程中监测矿柱变形及矿柱高度方向中间单元z方向的平均应力。矿柱破坏过程及其应力应变曲线如图16所示。
由图16可知，峰前阶段矿柱基本处于完整状态，峰值强度附近(见图16 B)剪切带仅发育了有限长度，此时的应力水平与矿柱强度之比为97%，可以推知处于正常承载状态的矿柱一般表现为完整状态；峰值强度后，剪切带迅速发展最终形成V形破坏(图16 D，应力水平与矿柱强度之比为92%)，V形破坏区深度为1.4 m，与矿柱尺寸之比为0.35，剪切带与水平方向夹角为56°，与理论值(π/4+φ/2)相符合。此外，V形破坏区内出现一条明显的劈裂裂隙。该裂隙从上下两侧剪切带向矿柱中部延伸直至贯穿整个V形破坏区。在峰值强度后期(图16 E、F)，V形破坏区内部张拉破裂逐步发展、累积。值得注意的是，V形破坏区形成时矿柱处于应力应变曲线的峰后阶段，承载能力逐步减弱，最终上部剪切带交叉贯通发生失稳破坏。另外，劈裂裂隙贯通整个V形破坏区以后，随着外部继续加载，其并没有继续向两侧延伸，这表明张拉裂隙的形成范围受剪切带控制。模拟结果中，方形矿柱强度为91 MPa，与完整岩石单轴抗压强度之比为0.38。采用LUNDER等[3]和POTVIN等[43]提出的硬岩矿柱强度公式计算模拟矿柱的强度均为99 MPa，模拟结果与计算结果比较接近，进一步说明了DISL方法模拟硬岩矿柱脆性破坏的有效性。
3 结论
1) 原位压缩模拟中，当卸荷时步大于某一临界值时，矿柱两侧发生V形破坏，矿柱整体形成沙漏状，因此DISL方法可以模拟硬岩矿柱脆性破坏时的最终形态。
2) 考虑矿柱岩体的不均质性时，不同均质度参数下屈服破坏单元主要分布在V形破坏区内及周围，其分布范围受低围压区及张拉区范围的控制。
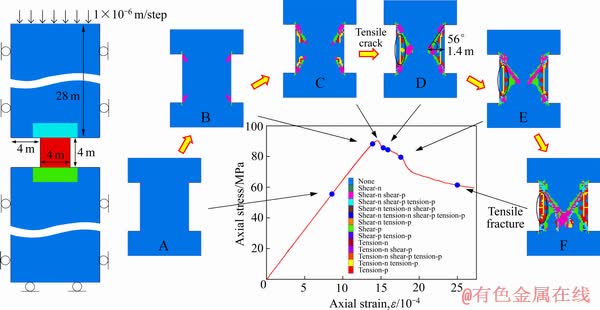
图16 矿柱单轴压缩数值模型及模拟结果
Fig. 16 Numerical model and simulation results of uniaxial compression of pillar
3) 均匀矿柱原位压缩模拟中，V形剪切带的形成主要以拉剪破坏为主，剪切带内部靠近矿柱边壁一侧，伴有张拉破坏单元。
4) 单轴压缩模拟中，峰后阶段矿柱两侧仍然产生V形破坏，并且张拉裂隙的形成范围受剪切带控制；矿柱模拟强度与经验公式计算强度比较接近，进一步验证了DISL方法的适用性。
REFERENCES
[1] PRITCHARD C J, HEDLEY D G F. Progressive pillar failure and rockbursting at Denison Mine[C]//Proceedings of the 3rd International Symposium on Rock Bursts and Seismicity in Mines. Rotterdam: A.A.Balkema Publishers, 1993.
[2] PERRAS M A. Understanding and predicting excavation damage in sedimentary rocks: A continuum based approach[D]. Ontario: Queen’s University, 2014: 265-267.
[3] LUNDER P J, PAKALNIS R C. Determination of the strength of hard-rock mine pillars[J]. Canadian Mining and Metallurgical Bulletin, 1997, 90(10): 51-55.
[4] 李地元. 高应力硬岩板裂破坏和应变型岩爆机理研究[D]. 长沙: 中南大学, 2010: 4-5.
LI Di-yuan. Study on the spalling failure of hard Rock and the mechanism of strain burst under high in-situ stresses[D]. Changsha: Central South University, 2010: 4-5.
[5] HAJIABDOLMAJID V, KAISER P K, MARTIN C D. Modelling brittle failure of rock[J]. International Journal of Rock Mechanics & Mining Sciences, 2002, 39(6): 731-741.
[6] 周 辉, 卢景景, 徐荣超, 张传庆, 孟凡震. 深埋硬岩隧洞围岩板裂化破坏研究的关键问题及研究进展[J]. 岩土力学, 2015, 36(10): 2737-2749.
ZHOU Hui, LU Jing-jing, XU Rong-chao, ZHANG Chuan-qing, MENG Fan-zhen. Critical problems of study of slabbing failure of surrounding rock in deep hard rock tunnel and research progress[J]. Rock and Soil Mechanics, 2015, 36(10): 2737-2749.
[7] CARTER T G, DIEDERICHS M S, CARVALHO J L. Application of modified Hoek-Brown transition relationships for assessing strength and post yield behaviour at both ends of the rock competence scale[J]. Journal of the Southern African Institute of Mining & Metallurgy, 2008, 108(6): 325-338.
[8] MARTIN C D. Seventeenth Canadian Geotechnical Colloquium: The effect of cohesion loss and stress path on brittle rock strength[J]. Canadian Geotechnical Journal, 1997, 34(5): 698-725.
[9] PELLI F, KAISER P K, MORGENSTERN N R. An interpretation of ground movements recorded during construction of the Donkin-Morien tunnel[J]. Canadian Geotechnical Journal, 1991, 28(2): 239-254.
[10] MARTIN C D, KAISER P K, MCCREATH D R. Hoek-Brown parameters for predicting the depth of brittle failure around tunnels[J]. Canadian Geotechnical Journal, 1999, 36(1): 136-151.
[11] STACEY T R, PAGE C H. Practical handbook for underground rock mechanics[M]. Clausthal-Zellerfeld: Trans Tech Publications, 1986.
[12] WAGNER H. Design and support of underground excavations in highly stressed rock[C]//Proceedings of the 6th ISRM Congress. Rotterdam: A.A.Balkema Publishers, 1987.
[13] CASTRO L A M, GRABINSKY M W, MCCREATH D R. Damage initiation through extension fracturing in a moderately jointed brittle rock mass[J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(3/4): 110-123.
[14] DIEDERICHS M S. Instability of hard rock masses: The role of tensile damage and relaxation[D]. Ontario: University of Waterloo, 1999: 1-20.
[15] WESSELOO J, STACEY T R. A Reconsideration of the Extension Strain Criterion for Fracture and Failure of Rock[J]. Rock Mechanics & Rock Engineering, 2016, 49(12): 4667－4679.
[16] KAISER P K, DIEDERICHS M S, MARTIN C D, SHARP J, STEINER W. Underground works in hard rock tunnelling and mining[C]//Proceedings of ISRM International Symposium. Florida: CRC Press, 2000.
[17] RAFIEI R H, MARTIN C D. Modeling the progressive failure of hard rock pillars[J]. Tunnelling and Underground Space Technology, 2018, 74: 71-81.
[18] MARTIN C D, MAYBEEB W G . The strength of hard-rock pillars[J]. International Journal of Rock Mechanics & Mining Sciences, 2000, 37(8): 1239-1246.
[19] DIEDERICHS M S. The 2003 Canadian geotechnical colloquium: Mechanistic interpretation and practical application of damage and spalling prediction criteria for deep tunnelling[J]. Canadian Geotechnical Journal, 2007, 44(9): 1082-1116.
[20] HOEK E, BROWN E T. Practical estimates of rock mass strength[J]. International Journal of Rock Mechanics & Mining Sciences, 1997, 34(8): 1165-1186.
[21] 曹 平, 曹日红, 赵延林, 张 科, 薄成志, 范文臣. 岩石裂纹扩展-破断规律及流变特征[J]. 中国有色金属学报, 2016, 26(8):1737-1762.
CAO Ping, CAO Ri-hong, ZHAO Yan-lin, ZHANG Ke, PU Cheng-zhi, FAN Wen-chen. Propagation-coalescence and rheologic fracture behavior of rock cracks[J]. The Chinese Journal of Nonferrous Metals, 2016, 26(8):1737-1762.
[22] FAIRHURST C, COOK N G W. The phenomenon of rock splitting parallel to the direction of maximum compression in the neighborhood of a surface[C]//Proceedings of the First Congress on International Society for Rock Mechanics. Lisbon: ISRM, 1966.
[23] HALLBAUER D K, WAGNER H, COOK N G W. Some observations concerning the microscopic and mechanical behaviour of quartzite specimens in stiff, triaxial compression tests[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1973, 10(6): 713-726.
[24] STACEY T R. A simple extension strain criterion for fracture of brittle rock[J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1981, 18(6): 469-474.
[25] NICKSIAR M, MARTIN C D. Evaluation of methods for determining crack initiation in compression tests on low-porosity rocks[J]. Rock Mechanics and Rock Engineering, 2012, 45(4): 607-617.
[26] LI D Y, LI C C, LI X B. Influence of sample height-to-width ratios on failure mode for rectangular prism samples of hard rock loaded in uniaxial compression[J]. Rock Mechanics and Rock Engineering, 2011, 44(3): 253-267.
[27] DOWDING C H, ANDERSSON C A. Potential for rock bursting and slabbing in deep caverns[J]. Engineering Geology, 1986, 22(3): 265-279.
[28] READ R S. 20 years of excavation response studies at AECL’s underground research laboratory[J]. International Journal of Rock Mechanics & Mining Sciences, 2004, 41(8): 1251-1275.
[29] MARTIN C D, CHANDLER N A. The progressive fracture of Lac du Bonnet granite[J]. International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts, 1994, 31(6): 643-659.
[30] SUORINENI F T, CHINNASANE D R, KAISER P K. A procedure for determining rock-type specific Hoek-Brown brittle parameters[J]. Rock Mechanics & Rock Engineering, 2009, 42(6): 849-881.
[31] SCHMERTMANN J H, OSTERBERG J H. An experimental study of the development of cohesion and friction with axial strain in saturated cohesive soils[C]//Proceedings of the Research Conference on Shear Strength of Cohesive Soils. New York: ASCE, 1960.
[32] WALTON G, ARZUA J, ALEJANO L R, DIEDERICHS M S. A laboratory-testing-based study on the strength, deformability, and dilatancy of carbonate rocks at low confinement[J]. Rock Mechanics & Rock Engineering, 2015, 48(3): 941-958.
[33] LANGFORD J C, DIEDERICHS M S. Reliable support design for excavations in brittle rock using a global response surface method[J]. Rock Mechanics and Rock Engineering, 2015, 48(2): 669-689.
[34] EDELBRO C. Different approaches for simulating brittle failure in two hard rock mass cases: A parametric study[J]. Rock Mechanics and Rock Engineering, 2010, 43(2): 151-165.
[35] EDELBRO C. Numerical modelling of observed fallouts in hard rock masses using an instantaneous cohesion-softening friction-hardening model[J]. Tunnelling & Underground Space Technology, 2009, 24(4): 398-409.
[36] KAISER P K, KIM B H. Characterization of strength of intact brittle rock considering confinement-dependent failure processes[J]. Rock Mechanics & Rock Engineering, 2015, 48(1): 107-119.
[37] 彭文斌. FLAC3D实用教程[M]. 北京: 机械工业出版社, 2007: 120-126.
PENG Wen-bin. Practical tutorial of FLAC3D[M]. Beijing: China Machine Press, 2007: 120-126.
[38] 刘 建, 赵国彦, 梁伟章, 吴 浩, 彭府华. 非均匀岩石介质单轴压缩强度及变形破裂规律的数值模拟[J]. 岩土力学, 2018, 39(S1): 505-512.
LIU Jian, ZHAO Guo-yan, LIANG Wei-zhang, WU Hao, PENG Fu-hua. Numerical simulation of uniaxial compressive strength and failure characteristics in nonuniform rock materials[J]. Rock and Soil Mechanics, 2018, 39(S1): 505-512.
[39] 梁正召, 唐春安, 张永彬, 马天辉. 准脆性材料的物理力学参数随机概率模型及破坏力学行为特征[J]. 岩石力学与工程学报, 2007, 27(4): 718-727.
LIANG Zheng-zhao, TANG Chun-an, ZHANG Yong-bin, MA Tian-hui. On probability model of physico-mechanical parameters of quasi-brittle materials and associated mechanical failure behaviors[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 27(4): 718-727.
[40] FENG X T, PAN P Z, ZHOU H. Simulation of the rock microfracturing process under uniaxial compression using an elasto-plastic cellular automaton[J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(7): 1091-1108.
[41] 苗胜军, 杨志军, 龙 超, 谭文辉. 脆性硬岩CWFS强度准则模型等效塑性参数优化研究[J]. 岩石力学与工程学报, 2013, 32(S1): 2600-2605.
MIAO Sheng-jun, YANG Zhi-jun, LONG Chao, TAN Wen-hui. Equivalent plastic parameters optimization research on CWFS failure criterion model of brittle hard rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S1): 2600-2605.
[42] 周 辉, 卢景景, 徐荣超, 张传庆, 陈 珺, 孟凡震. 硬脆性大理岩拉剪破坏特征与屈服准则研究[J]. 岩土力学, 2016, 37(2): 305-314.
ZHOU Hui, LU Jing-jing, XU Rong-chao, ZHANG Chuan-qing, CHEN Jun, MENG Fan-zhen. Research on tension-shear failure characteristics and yield criterion of hard brittle marble[J]. Rock and Soil Mechanics, 2016, 37(2): 305-314.
[43] POTVIN Y, HUDYMA M, MILLER H D S. Rib pillar design in open stope mining[J]. The Canadian Mining and Metallurgical Bulletin, 1989, 82(927): 31-36.
Modelling brittle failure of hard rock pillars based on DISL method
LIU Jian1, 2, ZHAO Guo-yan2, HU Jing-yun1
(1. State Key Laboratory of Safety Technology of Metal Mines, Changsha Institute of Mining Research Co., Ltd., Changsha 410012, China;
2. School of Resources and Safety Engineering, Central South University, Changsha 410083, China)
Abstract: Brittle failure with slabbing and spalling as a dominant failure mode of surrounding rock is a typical failure phenomenon in deep hard rock masses due to excavation activity. On the basis of brief introduction and comparison of four different approaches for modelling failure of brittle hard rock masses, the numerical tests of in-situ compression and uniaxial compression of hard rock pillars were carried out by means of FLAC3D based on the DISL method. The applicability of the DISL method was discussed and the brittle failure processes and characteristics of hard rock pillars were further explored. The results show that, in the in-situ compressive simulation, when the total unloading step is greater than a critical value, V-shaped failure occurs on both sides of the pillar, and the pillar forms an hourglass shape as a whole. Under different homogeneity indices, the yield elements are mainly distributed in and around V-shaped failure area and their distribution range is controlled by low confining pressure zone and tension zone. The V-shaped shear band is dominated by tension-shear failure and accompanied by tension failure elements in the inner part close to the pillar side wall. In the uniaxial compressive simulation, V-shaped failure still occurs on both sides of pillar in post-peak stage and the range of tension fracture is limited by shear band.
Key words: hard rock pillars; brittle failure; numerical simulation; DISL method; failure modes; strength characteristics
Foundation item: Project(2016YFC0600702) supported by the National Key Research and Development Plan of China
Received date: 2019-03-28; Accepted date: 2019-09-02
Corresponding author: ZHAO Guo-yan; Tel: +86-13507311842; E-mail: gy.zhao@263.net
(编辑 李艳红)
基金项目：国家重点研发计划资助项目(2016YFC0600702)
收稿日期：2019-03-28；修订日期：2019-09-02
通信作者：赵国彦，教授，博士；电话：13507311842；E-mail：gy.zhao@263.net
