基于蚁群优化算法的支持向量机参数选择及仿真

刘春波，王鲜芳，潘  丰

(江南大学 通信与控制工程学院，江苏 无锡，214122)

摘  要：基于支持向量回归机(SVR)模型的拟合精度和泛化能力取决于其相关参数的选取，以蚁群优化算法为基础，给出支持向量回归机参数优化的一种新方法。该方法以最小化k-fold交叉验证误差为目标，对支持向量回归机中的核参数σ和惩罚系数C由蚁群系统中的节点值体现，数值的优选通过蚂蚁对最优路径的选择进行确定。计算机仿真结果表明：与正交法、遗传算法等相比，该方法在参数优化方面有良好的鲁棒性能和较强的全局搜索能力；该方法用于青霉素发酵过程的建模研究，建模精度较高。

关键词：蚁群算法；支持向量回归机；参数选择；优化

中图分类号：TP391.9         文献标识码：A         文章编号：1672-7207(2008)06-1309-05

Parameters selection and stimulation of support vector machines based on ant colony optimization algorithm

LIU Chun-bo, WANG Xian-fang, PAN Feng

(School of Communications and Control Engineering, Jiangnan University, Wuxi 214122, China)

Abstract: Based on the fact that the regression accuracy and generalization performance of the support vector regression (SVR) models depend on a proper setting of its parameters, a new trial was applied in parameters selection. The new optimal selection approach of SVR parameters was put forward based on ant colony optimization (ACO) algorithm. The k-fold cross-validation error was used as the fitness function of ACO. The node values in ant system were reflected by the kernel parameter σ and regularization parameter C of SVR. The optimal values are equal to those of the best route which are decided by ants. Simulation results show that the optimal selection approach based on ACO has good robustness and strong global search capability. The method used for the research of modeling in the penicillin ferment process obtains higher accuracy.

Key words: ant colony algorithm; support vector regression; parameters selection; optimization

支持向量机^[1-3](Support vector machines, SVM)是一种基于统计学习理论的机器学习方法，能较好地用于解决小样本、非线性等实际问题，已成为智能技术领域研究的热点^[4-5]。基于支持向量机方法的回归估计以可控制的精度逼近任一非线性函数，同时具有全局最优、泛化能力较强等性能，其应用非常广泛^[6]。实践表明，SVM的性能与核函数的类型、核函数的参数以及惩罚系数C有很大关系。因此，研究SVM参数选择的方法，对支持向量机的发展有很重要的实际意义。通常，支持向量机参数选择的方法有正交法、梯度下降法(Gradient descend, GD)^[7]、遗传算法(Genetic algorithm, GA)^[8]、粒子群优化(Particle swarm optimization, PSO)^[9]等。在此，本文作者提出一种基于蚁群算法的SVM参数选择方法。蚁群算法具有并行性、正反馈性、求解精度高、鲁棒性强等特点。蚁群算法是一种新型的模拟进化算法，由Dorigo等^[10-12]提出，称为蚁群系统。实验结果表明，蚂蚁在运动过程中会留下一种分泌物，其后面的蚂蚁可根据前边走过的蚂蚁所留下的分泌物选择其要走的路径。因此，蚂蚁群体的集体行为实际上构成一种学习信息的正反馈现象，蚂蚁之间通过这种信息交流寻求通向食物的最短路径。蚁群算法模拟了这种优化机制，即通过个体之间的信息交流与相互协作最终找到最优解。

1  支持向量回归机

支持向量回归算法的基本思想是通过一个非线性映射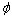，将数据x映射到高维的特征空间F，并在该空间进行线性回归。因此，对于给定的观测数据集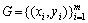可以用下式进行回归估计：

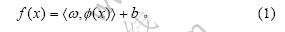
其中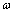，和b表示回归因子，可通过对以下正则化风险泛函最小化获得：

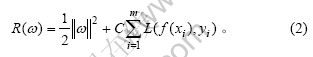
C为惩罚系数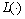；为损失函数，通常取一次不敏感损失函数：

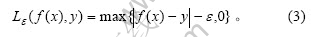
将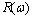最小化可得：

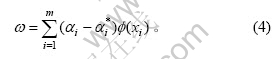
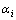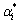其中：和是最小化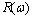对偶问题的解。将代入式(1)得：

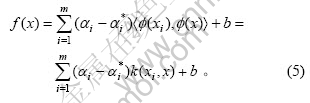
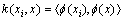，称为核函数，它是对称的正实数函数，同时满足Mercer条件。常用的核函数有径向基核函数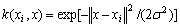和多项式核函数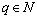，，d≥0。

当b为边界上的1点时，便可根据KKT最优条件定理进行计算，但考虑到稳定性，一般取边界点上的平均值：

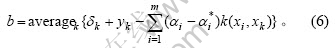
其中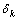：为预测误差。

可见，在支持向量回归估计算法中，核函数的选取决定了输入空间到特征空间映射的方式，惩罚系数C用于平衡训练误差和模型复杂度。

2  实现基于蚁群算法的SVM参数的选择

2.1  SVM参数的蚁群算法寻优

蚁群算法的基本原理见参考文献[13-16]。本文选用k-fold交叉验证误差作为目标值E，以径向基函数为例，用ACO算法对核参数σ和惩罚系数C进行优选。用蚁群算法所搜索出的最终路径代表模型此时具有最好的建模精度。C和σ在蚁群系统中由节点值体现，激素物质遗留在蚂蚁所走过的每个节点(相当于TSP问题中的城市)上。SVM参数优化的蚁群系统不是根据路径长度来更新信息素的浓度，而是根据目标函数值来更新信息素的浓度。目标函数中隐含各蚂蚁所走过的所有节点的信息以及所建模型当前的准确度。以SVM的参数C和σ作为待优化的变量，一般程序运行前要先通过专家经验来确定C和σ的有效位和准确度，若确定不当，则会影响建模效果。这样，程序运行完后，便能从蚂蚁的最优化路径中得到相应的数值，结果如图1所示，其中：X表示所寻参数的有效位，Y表示0~10的无量纲数字；C和σ的有效位各为5，C的最高位为百位，其数值范围为100.00~ 999.99；σ的最高位为个位，其数值范围为1.000 0~ 9.999 9。这样，蚂蚁的最优化路径代表的数值为C=750.45，σ=3.994 6。

用knot(x_i, y_{i, j})表示1个节点，x_i为线段L_i的横坐标，y_{i, j}为线段L_i上节点j的纵坐标。设τ(x_i, y_{i, j}, t)表示t时刻节点knot(x_i, y_{i, j})上遗留的信息素，初始时刻各节点上的信息素相等，即τ(x_i, y_{i, j}, 0)=γ (其中，γ为常数，i=1~n, j=0~9)，初始时刻信息素增量为零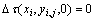。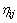表示由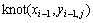到knot(x_i, y_{i, j})的期望程度，可以根据启发算法及问题的情况来确定，此值与上一次循环的目标值E有关。设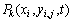表示时刻t第k只蚂蚁由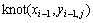点向knot(x_i, y_{i, j})爬行的概率，则有

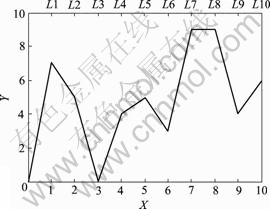
图1  蚁群算法优化C和σ参数

Fig.1  Optimizing parameters C and σ using ACO

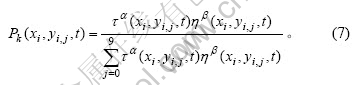
假设在初始时刻t=0，所有蚂蚁位于坐标原点O，那么，经过n个时间单位后，所有的蚂蚁都从起始点爬到终点，此时，可根据如下公式调整各路径点上的信息量：

式中：E_k表示第k只蚂蚁在本次循环中对应的交叉验证误差值，Q为常数。

2.2  蚁群算法步骤的实现

算法具体步骤描述如下。

步骤1：设定蚂蚁数m，并给每只蚂蚁k(k=1~m)各定义一个具有n个元素的一维数组path_k。在path_k中依次存放第k只蚂蚁要经过的n个节点的纵坐标，可用来表示第k只蚂蚁的爬行路径。其中，n为所优化参数的总有效位。

步骤2：令时间计数器t=0，循环次数N=0，设定最大循环次数N_max以及初始时刻各节点上信息量τ(x_i, y_{i, j}, 0)的值γ(i=1~n, j=0~9)，令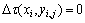，将全部蚂蚁置于起始点O。

步骤3：置变量i=1。

步骤4：利用式(7)计算这些蚂蚁向线段L_i上每个节点转移的概率；根据这些概率，采用赌轮选择方法为每只蚂蚁k(k=1~m)在线段L_i上选择1个节点，并将蚂蚁k移到该节点，同时，将该节点的纵坐标存入path_k的第i个元素中。

步骤5：置i=i+1，若i≤n，则跳转到步骤4；否则，跳转到步骤6。

步骤6：根据蚂蚁k(k=1~m)所走过的路径，即数组path_k，计算该路径对应的C和σ。其中，C和σ的有效位、数量级编程前通过专家经验确定。

步骤7：将训练样本平均分割成k个互不包含的子集S₁, S₂, …, S_k。

步骤8：根据计算的{C, σ}训练SVM，计算k-fold交叉验证误差。

步骤8a：初始化i=1；

步骤8b：S_i子集留作检验集，其余子集合的并集作为训练集，训练SVM。

步骤8c：计算第i子集的泛化误差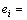 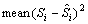，令i=i+1，重复步骤8b，直到i=k+1为止；

步骤8d：计算k次泛化误差的平均值，得到k-fold交叉验证误差；

步骤9：以k-fold交叉验证误差作为适应值，记录本次循环的最优路径。

步骤10：令t=t+n，N=N+1，根据式(8)更新每个节点上的信息量，并将path_k (k=1~m)中的所有元素  清零。

步骤11：若N＜N_max，且整个蚁群尚未收敛到走同一条路径，则再次将全部蚂蚁置于起始点O并跳转到步骤3；若N＜N_max，且整个蚁群已收敛到走同一条路径，则算法结束，输出最优路径计算相应的C和σ。

3  仿真示例

为验证上述算法的有效性，选用SVM回归中常用的函数进行仿真，所有试验都是在主频为2.0 GHz，内存为256 MB的PC机及MTALAB 7.0软件平台上完成。

取一维sin c函数如下：

。

其中：v是均值为0、方差为0.1的高斯噪声。在输入变量域内取100个数据构成SVM的训练样本，以最小化5-fold交叉验证误差为目标，利用ACO算法对径向基核函数参数σ和惩罚系数C进行优选。其中，SVM采用ε=0.1的一次不敏感损失函数；ACO中的参数选择m=30，N_max=1 000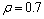，，Q=100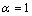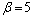，，(其中，参数的选择原则参考文献[17]，C和σ的有效位和准确度通过经验合理确定)。图2显示了根据本文方法得到的参数对SVM进行训练的结果，可见，拟合效果很好。为便于比较，分别利用正交法(2因素10水平)和遗传算法(GA，交叉概率为0.8，变异概率为0.2%，种群数和最大迭代次数与ACO算法的一样)进行多次试验，并随机产生50个数据作为测试集，对所得SVM模型进行测试，平均结果见表1。从表1可见，利用本文方法所得的SVM模型支持向量个数最少，测试均方误差最小。

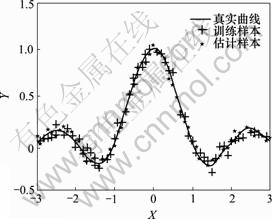
图2  sin c函数仿真结果

Fig.2  Simulation results of sin c

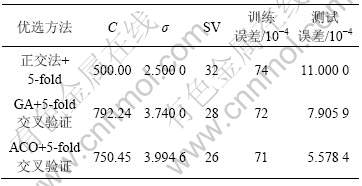
表1  SVM参数选择试验的不同方法平均结果比较

Table 1  Average results of parameters selection of SVM by different methods

4  基于ACO算法的SVM建模应用

青霉素是青霉素产生菌的次级代谢产物。青霉素发酵属于半连续发酵方式，是一个非常复杂的多变量相互藕合的生物化学过程，具有高度的非线性、时变性和不确定性，很难给出一个精确的数学模型。影响青霉素发酵产率的因素很多，主要有温度、pH值、基质浓度、溶氧饱和度、菌丝浓度、菌丝生长速度、菌丝形态等^[18]。本文采用SVM方法建立青霉素发酵效价预估模型。采用RBF核函数，ε=0.006，第1次训练样本数15，测试样本数为55，c=657.14，=52.536，通过本文参数寻优的方法获得，训练误差为0.033 625，测试误差为0.032 529。其中，ACO中参数m=7，N_max=100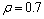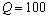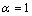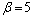，，，，。其预测仿真图形如图3所示。第2次训练样本数50，测试样本数为200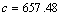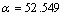，，，通过本文参数寻优的方法获得，训练误差为0.024 127，测试误差为0.025 403。其中，ACO中的参数m=20，N_max=10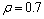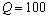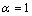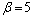，，，，。由此可见，建模效果良好，且ACO在SVM参数寻优中有较强的鲁  棒性。

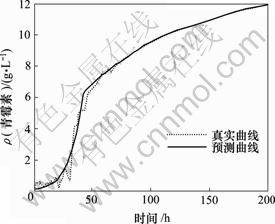
图3  青霉素仿真结果

Fig.3  Simulation results of penicillin

5  结  论

a. 以蚁群优化算法为基础，给出了支持向量回归机参数优化的一种新方法。蚁群路径上的每一个节点都包含所需优化参数的部分信息。1条完整的路径可以把所需优化的参数间接地表示出来，这样，从最优路径中计算出的参数值便是最优参数。

b. 仿真结果表明，用蚁群算法寻优得出的参数在回归实验中支持向量数最少为26，比正交法和遗传算法的最少支持向量数少(分别为32和28)，但训练效果和预测效果最佳，说明蚁群算法在参数优化方面具有良好的鲁棒性和较强的全局搜索能力，能提高建模  精度。

c. 蚁群算法用于青霉素发酵过程的建模研究，取得了满足的建模效果。青霉素发酵过程具有高度的非线性、时变性和不确定性，很难给出一个精确的数学模型。而基于蚁群算法的支持向量机对某一样本的训练误差为0.024 127，测试误差为0.025 403，建模效果良好。

参考文献：

[1] Vapnik V N. The nature of statistical learning heory[M]. New York: Springer-Verlag, 1995.

[2] Vapnik V N. Statistical learning theory[M]. New York: Springer, 1998.

[3] Vapnik V N. The nature of statistical learning [M]. 2nd ed. New York: Springer, 2000.

[4] Smola A J, Scholkopf B. A tutorial on support vector regression[R]. NeuroCOLT2 Technical Report NC2-TR- 1998-030. London: Royal Holloway College, 1998.

[5] Sanchez A D. Advanced support vector machines and kernel methods[J]. Neurocomputing, 2003, 55(1): 5-20.

[6] 杜树新, 吴铁军. 用于回归估计的支持向量机方法[J]. 系统仿真学报, 2003, 15(11): 1580-1585, 1633.
DU Shu-xin, WU Tie-jun. Support vector machines for regression[J]. Journal of System Simulation, 2003, 15(11): 1580-1585, 1633.

[7] Chappelle O, Vapnik V, Bousquet O, et al. Choosing multiple parameters for support vector machines[J]. Machine Learning, 2002, 46(1): 131-160.

[8] ZHENG Chun-hong, JIAO Li-cheng. Automatic parameters selection for SVM based on GA[C]//Proceedings of the the 5th World Congress on Intelligent Control and Automation. Piscataway. NJ: IEEE Press, 2004: 1869-1872.

[9] SHAO Xin-guang, YANG Hui-zhong, CHEN Gang. Parameters selection and application of support vector machines based on particle swarm optimization algorithm[J]. Control Theory and Applications, 2006, 23(5): 740-743, 748.

[10] Dorigo M, Stutzle T. Ant colony optimization[M]. Cambridge: MIT Press, 2004.

[11] Dorigo M, Blum C. Ant colony optimization theory: A survey[J]. Theoretical Computer Science, 2005, 344(2/3): 243-278.

[12] Dorigo M, Gambardella L M. Ant colony system:a cooperative learning approach to the traveling salesman problem[J]. IEEE Transaction on Evolutionary Computation, 1997, 1(1): 53-66.

[13] Colorni A, Dorigo M, Maniezzo V, et al. Distributed optimization by ant colonies[C]//Proceedings of the 1st European Conference on Artifical Life. Paris: Elesvier Publishing, 1991: 134-142.

[14] Dorigo M, Maniezzo V, Colorni A. Ant system: Optimization by a colony of cooperating agents[J]. IEEE Transaction on Systems, Man, and Cybernetics: Part B, 1996, 26(1): 29-41.

[15] 谭冠政, 李文斌. 基于蚁群算法的智能人工腿最优化PID控制器设计[J]. 中南大学学报: 自然科学版, 2004, 35(1): 91-96.
TAN Guan-zheng, LI Wen-bin. Design of ant algorithm based optimal PID controller and its application to intelligent artificial leg[J]. Journal of Central South University: Science and Technology, 2004, 35(1): 91-96.

[16] LIU Chun-bo, PAN Feng, YANG Dan. Resolution of CTSP based on improved ant colony algorithm[C]//ZHANG Si-ying, WANG Fu-li. Proceedings of Chinese Control and Decision Conference. Shenyang: Northeastern University Press, 2007: 869-872.

[17] 詹士昌, 徐 婕, 吴 俊. 蚁群算法中有关算法参数的最优选择[J]. 科技通报, 2003, 19(5): 381-386.

ZHAN Shi-chang, XU Jie, WU Jun. The optimal selection on the parameters of the ant colony algorithm[J]. Bulletin of Science and Technology, 2003, 19(5): 381-386.

[18] 于乃功, 阮晓钢. 模拟青霉素发酵过程中菌体生长动态的细胞自动机模型[J]. 生物物理学, 2004, 20(2): 155-162.
YU Nai-gong, RUAN Xiao-gang. A cellular automata model for simulating penicillin fermentation process biomass growth[J]. Acta Biophysica Sinica, 2004, 20(2): 155-162.

收稿日期：2008-01-21；修回日期：2008-03-05

基金项目：国家“863”计划项目(2006AA020301)

通信作者：潘  丰(1963-)，男，江苏苏州人，博士，教授，博士生导师，从事过程控制、发酵建模等研究；电话：0510-85912125；E-mail: pan_feng_63@163.com